期中真题专项复习 04 证明题(含解析)--2024-2025学年七年级数学下册(北师大版2024)
文档属性
| 名称 | 期中真题专项复习 04 证明题(含解析)--2024-2025学年七年级数学下册(北师大版2024) |  | |
| 格式 | docx | ||
| 文件大小 | 859.5KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-03-29 13:30:55 | ||
图片预览




文档简介
2024-2025学年七年级数学下册(北师大版2024)
期中真题专项复习 04 证明题
一、证明题
1.(2024七下·慈溪期中)如图,在四边形中,,.
(1)求的度数;
(2)若平分交于点,,求证:.
2.(2024七下·义乌期中)如图,D是BC上一点,DE∥AB,交AC于点E,F是AB上一点,且∠DEC+∠AFD=180°.
(1)求证:DF∥AC;
(2)若∠B+∠C=130°,求∠FDE的度数.
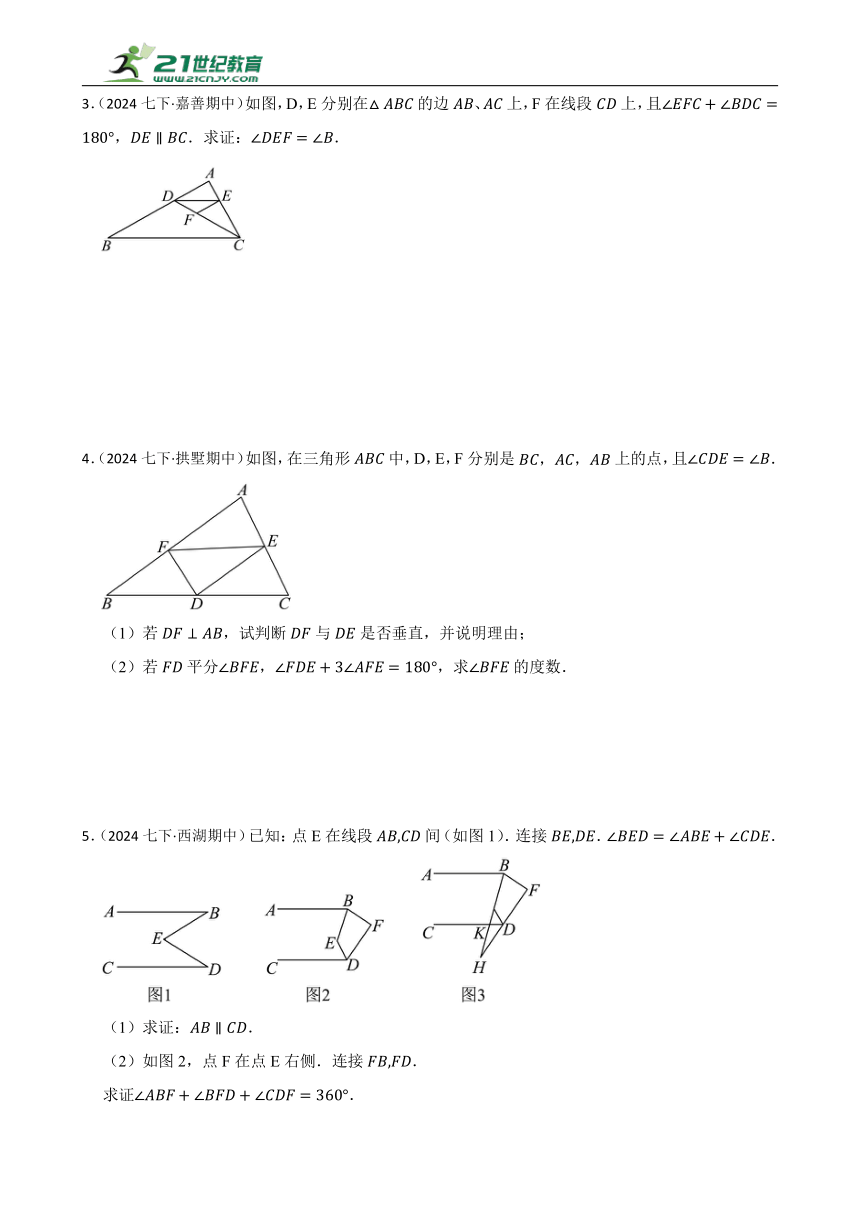
3.(2024七下·嘉善期中)如图,D,E分别在的边、上,F在线段上,且,.求证:.
4.(2024七下·拱墅期中)如图,在三角形中,D,E,F分别是上的点,且.
(1)若,试判断与是否垂直,并说明理由;
(2)若平分,,求的度数.
5.(2024七下·西湖期中)已知:点E在线段间(如图1).连接..
(1)求证:.
(2)如图2,点F在点E右侧.连接.
求证.
(3)如图3在(2)的条件下,线段,的延长线交于点H.交于点K.当平分,平分,,时,求的度数.
6.(2024七下·澄城期中)已知,如图,,,求证:,请完成解答过程.
证明:(已知)
▲ ( )
又(已知)
▲ ( )
▲ (两直线平行,内错角相等)
(等量代换)
7.(2024七下·子洲期中)如图,已知点A,B,D在一条直线上,,∠1=∠2,请填写∠B=∠C的理由.
解:因为,所以∠1= ▲ ( ),
∠2= ▲ ( ).
2因为∠1=∠2,所以∠B=∠C( ).
8.(2024七下·潮州期中)如图,已知点P在CD上,∠BAP+∠APD=180°,∠1=∠2,求证:∠E=∠F.
9.(2024七下·凉州期中)如图,若,,那么吗?请在下面的解答过程中填空或在括号内填写理由.
解:理由如下:
(已知),
____________(______),
______(______)
又(已知),
______(______)
(______).
10.(2024七下·福田期中)请将下列说理过程补充完整:
如图:,,,试说明.
解:因为(已知),
所以(______),
因为(已知),
所以______(两直线平行,内错角相等),
因为(已知),
所以_____________(______),
即,
所以(______).
11.(2024七下·上海市期中)如图,如图,已知,,,求的度数.
12.(2024七下·北京市期中)如图,,,求证.完成下面的证明过程.
证明:∵,,
∴(同角的补角相等).
∴ (内错角相等,两直线平行).
∴( ).
又∵(已知),
∴ (等量代换)﹒
∴( ).
∴(两直线平行,同位角相等).
13.(2024七下·柳州期中)如图,已知∠1=∠2,∠B=∠C,求证:AB∥CD.
14.(2024七下·镇海区期中)如图,已知F,E分别是射线上的点.连接,其中平分,平分,.
(1)试说明;
(2)若,求的度数.
15.(2024七下·惠阳期中)如图,已知AB∥CD,∠B+∠D=180°.求证:BC∥ED.
16.(2024七下·广州期中) 如图,已知,,垂足分别为D、F,,试说明:.请补充说明过程,并在括号内填上相应的理由.
解:,(已知),
( ),
( ).
( )
(已知).
( ).
∴ ( )
( ).
17.(2024七下·宜春期中)如图,已知,.求证:.请完善证明过程,并在括号内填上相应依据.
证明:∵(已知),
∴ ( ).
又∵(已知),
∴ ( ),
∴ ( ),
∴(两直线平行,同位角相等).
18.(2024七下·霞浦期中)填空:把下面的推理过程补充完整,并在括号内注明理由.
如图,已知BC分别交AB、DE于点B、C,且∠ABC+∠ECB=180°,∠P=∠Q.求证:∠1=∠2.
证明:因为∠ABC+∠ECB=180°(已知),
所以AB∥DE( ).
所以∠ABC=∠BCD( ).
因为∠P=∠Q(已知),
所以PB∥CQ( ).
所以∠PBC=( )(两直线平行,内错角相等).
因为∠1=∠ABC﹣( ),
∠2=∠BCD﹣( ),
所以∠1=∠2(等量代换).
19.(2024七下·黄埔期中)根据解答过程填空(理由或数学式).
已知:如图,,,求证:.
证明:∵(邻补角定义),
又∵(已知),
∴( ),
∴( ),
∴( )
∵(已知),
∴( ),
∴( ),
∴( ).
20.(2024七下·清城期中)如图,在三角形中,,垂足为,为上的点,,垂足为,点在上,连接,若,求证:.
21.(2024七下·天津市期中)如图,已知,,,垂足为A,请在横线上补全求的度数的解题过程或依据.
解:∵(已知).
∴ ( ).
∵已知),
∴ (等量代换).
∴
∴ (两直线平行,同旁内角互补).
又∵(已知),
∴ ( ).
∴ (等式的性质).
22.(2024七下·东昌府期中)如图,直线AB、CD相交于点O,OM⊥AB.
(1)若∠1=∠2,证明:ON⊥CD;(2)若∠1=∠BOC,求∠BOD的度数.
23.(2024七下·永州期中)填空:如图,在四边形中,分别于相交于点E、F.,,试说明.
解:∵,
∴____________.(______),
又∵,
∴____________(______),
∴____________(______).
24.(2024七下·澄海期中)如图,已知,,平分,平分,,求证:
请将下列证明过程中的空格补充完整
证明:∵,
( )
平分,平分
( )
=
( )
(两直线平行,内错角相等)
即( )
25.(2024七下·西城期中)已知:如图,,,.求证:平分.
证明:∵,,
∴,(_______).
∴.
∴__________(_______).
∴(_________).
(_________).
又∵,∴(等量代换).
∴平分.
26.(2024七下·北京市期中)请你补全证明过程或推理依据:
已知:如图,四边形,点E、F分别在边两方的延长线上,连接,若,.
求证:.
证明:∵点E在的延长线上(已知)
∴
又∵(已知)
∴ ( )
又∵(已知)
∴ ( )
∴( )
∴( )
27.(2024七下·西工期中)已知:如图所示,,和分别平分和,.求证:.
证明:∵和分别平分和(已知)
∴ ,
.( )
又∵(已知),
∴∠ (等量代换).
又∵(已知),
__________(等量代换),
∴( ).
28.(2024七下·滑县期中)如图,已知,,,将下面“求证:”的过程补充完整.
证明:∵,
∴,(判定依据:________,两直线平行)
∴________(两直线平行,内错角相等)
又∵,
∴________=________(等量代换),
∴________(判定依据:________,两直线平行)
又∵,
∴________°,(垂直的定义)
∴________°,(两直线平行,________)
∴.
29.(2024七下·龙口期中)如图,已知,,求证:.
下面是小明同学不完整的证明过程,请你在横线上补充完整,并在括号里填上每一步的推理依据.
证明:∵(已知),
∴_________,
∵(_________),
∴(_________),
∴(_________),
∴_________(两直线平行,同旁内角互补),
∵(_________),
∴(_________).
30.(2024七下·北京市期中)完成下面的证明.已知:如图,AC⊥BD,EF⊥BD,∠A=∠1.求证:EF平分∠BED.
证明:∵AC⊥BD,EF⊥BD,
∴∠ACB=90°,∠EFB=90°.(______)
∴∠ACB=∠EFB.
∴_____________.(______)
∴∠A=∠2.(两直线平行,同位角相等)
∠3=∠1.(_______)
又∵∠A=∠1,
∴∠2=∠3.
∴EF平分∠BED.
31.(2024七下·鄞州期中)如图,在三角形中,点D在上,交于点E,点F在,.
(1)试说明:;
(2)若,求的度数.
32.(2024七下·杭州期中)如图,点是上一点,,交于点,且.
(1)求证:;
(2)若,求的度数(用含的代数式表示).
33.(2024七下·高州期中)已知:如图,∠D=∠A,∠B=∠FCB
求证:ED//CF
34.(2024七下·白云期中)如图,AD∥BE,AE平分∠BAD,CD与AE相交于F,∠CFE=∠E.求证:AB∥CD.
35.(2024七下·厦门期中)请在下列空格内填写结论或理由,完成推理过程.
如图,于D,点E在的延长线上,于G,交于点F,.
求证:平分.
证明:∵于D,于G(已知)
∴(______)
∴______(同位角相等,两直线平行)
∴(______)
______(两直线平行,同位角相等)
又∵(已知)
∴(等量代换)
∴平分(角平分线的定义)
36.(2024七下·瓜州期中)如图,已知平分交于点E.
(1)试说明:与的关系
(2)若于点,求的度数.
37.(2024七下·滨海期中)(1)已知:如图,且,求证.
证明:∵,(已知),
∴(______),
∵(已知)
∵(______),
∴______,
∴(______);
(2)已知:如图,直线,被所截,,求证:.
证明:∵(______),
又∵(已知),
∴______(______),
∴(______).
38.(2024七下·余姚期中)如图,于点D,点F是上任意一点,过点F作于点E,且.
(1)求证:;
(2)若,平分,求的度数.
39.(2024七下·柘城期中)中国汉字博大精深,方块文字智慧灵秀,奥妙无穷.如图(1)是一个“互”字,如图2是由图1抽象出的几何图形,其中,,点,,在同一直线上,点,,在同一直线上,且.
求证:.
证明∶如图,延长交于点.
∵(已知),
∴(_________)
又∵(已知),
∴(________)
∴____________(________)
∴_______+_______(_______)
∵(已知),
∴_______(__________)
∴.
40.(2024七下·凉州期中)先阅读再解答:
(1)如图1,,试说明:;
(2)已知:如图2,,求证:;
(3)已知:如图3,,.求证:.
41.(2024七下·滨江期中)如图,在中,点C是边上一点,点E是外一点,连结,使得,且.
(1)与相等吗?请说明理由;
(2)若,,求的度数.
42.(2024七下·滨海期中)如图所示,已知,平分,平分,,试说明:.
解:(______),
又平分,
______(______),
又平分,
______,
.(______)
,
____________
(______)
43.(2024七下·清苑期中)如图,点D,E是线段上的点,点F是线段上的点,,点H是上的点,且.求证:.
请将下面的证明过程补充完整:
证明:∵,
∴______.(理由:_________)
∵,
∴_____.
∴____________.(理由:______)
∴.
44.(2024七下·蕲春期中)填空,完成下列证明过程,并在括号中注明理由.
如图,已知∠BEF+∠EFD=180°,∠AEG=∠HFD,求证:∠G=∠H.
解:∵∠BEF+∠EFD=180°,(已知).
∴AB// ( ).
∴ =∠EFD( ).
又∵∠AEG=∠HFD,
∴∠AEF﹣∠AEG=∠EFD﹣∠HFD,即∠GEF= .
∴ //FH( ).
∴∠G=∠H.( ).
答案解析部分
1.(1)解:解:,
,
,
,
的度数是110°;
(2)证明:∵平分交于点,=110°,
,
,
,
,
,
.
(1)根据平行线的性质得,最后进行计算即可求出答案;
(2)根据角平分线的定义求出∠DAE=55°,再根据平行线的性质得∠AEB=∠DAE=55°,从而得∠AEB=∠BCD,最后根据平行线的判定得AE∥CD.
2.(1)证明:∵,
∴,
∵,
∴,
∴;
(2)解:∵,
∴,
根据(1)可知:,,
∵,
∴,
∵,
∴.
(1)根据平行线的性质得到,进而结合题意得到,再根据平行线的判定即可求解;
(2)先根据题意得到,进而根据(1)可知:,,从而根据平行线的性质即可求解。
3.证明:∵,,
∴,
∴,
∴,
∵,
∴,
∴.
先证明,可得,于是根据平行线的性质可得,再根据平行线性质得,等量代换即可证明结论.
4.(1)解:,理由如下:
,
,
∴∠BFD=∠FDE.
,
,
,
.
(2)解:平分,
,
,
,∠AFE=∠FED.
∵△FDE中,∠FDE+∠DFE+∠FED=2∠FDE+∠AFE=180°,
又∵∠FDE+3∠AFE=180°,
∴2∠FDE+∠AFE=∠FDE+3∠AFE,即∠FDE=2∠AFE.
∴5∠AFE=180°,
解得:∠AFE=36°,
∴∠BFE=2∠FDE=4∠AFE=144°.
5.(1)解:如图,过点E作,
∴,
∴,
∵,
∴,
∴,
∴;
(2)解:如图,过点F作,
∵,
∴,
∴,
∴,
即;
(3)解:设,∵平分,平分,
∴,
∴,
由(1)得:,
∵,
∴,
∵,
∴,
∴,
∴,
∴,
∴,
∵,
∴,
解得:,
∴,
∴.
6.证明:∵AD∥BE(已知)
∴∠A=∠3,(两直线平行,同位角相等)
又∵∠1=∠2(已知)
∴AC∥DE( 内错角相等,两直线平行)
∴∠3=∠E(两直线平行,内错角相等)
∴∠A=∠E(等量代换)
故答案为:3,两直线平行,同位角相等;DE,内错角相等,两直线平行;E
通过对已知的观察分析可以看出,由两直线平行,同位角相等可以得到∠A=∠3,再由内错角相等,两直线平行,推出AC∥DE,进而由 两直线平行,内错角相等 得到∠3=∠E,最后由等量代换得∠A=∠E.
7.因为,所以∠1=∠B(两直线平行,同位角相等),
∠2=∠C(两直线平行,内错角相等).
因为∠1=∠2,所以∠B=∠C(等量代换).
利用平行线的性质求出∠1=∠B和∠2=∠C,通过等量转化即可推出 ∠B=∠C .
8.证明:∵∠BAP+∠APD=180°,(已知)
∴AB∥CD.(同旁内角互补,两直线平行)
∴∠BAP=∠CPA.(两直线平行,内错角相等)
∵∠1=∠2,(已知)
∴∠BAP-∠1=∠CPA-∠2
∴∠EAP=∠FPA.
∴AE∥PF.(内错角相等,两直线平行)
∴∠E=∠F.(两直线平行,内错角相等)
利用同旁内角互补,两直线平行可证得AB∥CD,利用平行线的性质可推出∠BAP=∠CPA,结合已知条件可证得∠EAP=∠FPA;再利用内错角相等,两直线平行可证得AE∥PF,然后利用平行线的性质可证得结论.
9.;;内错角相等,两直线平行;;两直线平行,内错角相等;;等量代换;同位角相等,两直线平行.
10.两直线平行,内错角相等;;,;等式的性质;等量代换
11.
12.,两直线平行,内错角相等,,同位角相等,两直线平行
13.解:∵∠1=∠2(已知),∠1=∠4(对顶角相等)
∴∠2=∠4(等量代换)
∴EC∥BF(同位角相等,两直线平行)
∴∠C=∠3(两直线平行,同位角相等)
又∵∠B=∠C(已知)
∵∠B=∠3(等量代换)
∴AB∥CD(内错角相等,两直线平行)
根据对顶角相等,得到∠1=∠4,得到∠2=∠4,由EC∥BF,得到∠C=∠3,根据∠B=∠C,得出∠B=∠3,结合内错角相等,两直线平行,即可证得AB∥CD.
14.(1)解:如图,,
平分,
,
,
(2)解:如图
,
,
,
,
平分,
,
,
,
,
,
,
的度数为
(1)根据等边对等角得到,根据角平分线得到,即可得到,再根据平行线的判定定理得到结论即可;
(2)先得到,再根据两直线平行,内错角相等得到,根据角平分线的定义得到,求出∠3的度数,即可得到的度数解题.
15.证明:∵,
∴,
∵,
∴,
∴.
由两直线平行,内错角相等可得∠B=∠C,由等量代换可得∠C+∠D=180°,然后根据“同旁内角互补,两直线平行”可求解.
16.垂直的定义;同位角相等,两直线平行;;两直线平行,同旁内角互补;同角的补角相等;;内错角相等,两直线平行;两直线平行,同位角相等
解:,(已知),
( 垂直的定义 ),
( 同位角相等,两直线平行 ).
∠1( 两直线平行,同旁内角互补 )
(已知).
( 同角的补角相等 ).
∴DG( 内错角相等,两直线平行 )
( 两直线平行,同位角相等 ).
根据垂直的定义得∠ADB=∠EFB=90°,由同位角相等,两直线平行,得AD∥EF,由二直线平行,同旁内角互补,得∠1+∠2=180°,结合已知,由同角的补角相等得∠1=∠3,由内错角相等,两直线平行,得AB∥DG,最后根据两直线平行,同位角相等可得∠GDC=∠B.
17.;两直线平行,内错角相等;;等量代换;;内错角相等,两直线平行
18.同旁内角互补,两直线平行;两直线平行,内错角相等;内错角相等,两直线平行;∠BCQ;∠PBC;∠BCQ
19.同角的补角相等;内错角相等,两直线平行;两直线平行,内错角相等;等量代换;同位角相等,两直线平行;两直线平行,同位角相等
20.证明:∵,,∴,
∴,
∴,
∴
∵,
∴,
∴,
∴.
本题考查平行线的判定与性质,根据,,得到,证得,结合,得到,结合内错角相等,两直线平行,证得,再由两直线平行,同位角相等,即可证得.
21.;两直线平行,内错角相等;;;;;垂直的定义;
22.(1)ON⊥CD.(2)60°.
23.1;2;两直线平行,内错角相等;2;3;两直线平行,同位角相等;1;3;等量代换.
24.两直线平行,同位角相等;角平分线的定义;;同位角相等,两直线平行;;垂直的定义.
25.垂线的定义;;同旁内角互补,两直线平行;两直线平行,同位角相等;两直线平行,内错角相等;
26.1;1;同角的补角相等;3;等量代换;内错角相等,两直线平行;两直线平行,内错角相等
27.角平分线的定义;;同位角相等,两直线平行
28.同位角相等;内错角相等;90;90;同位角相等
29.;已知;等量代换;同位角相等,两直线平行;;对顶角相等;等量代换
30.垂直定义;AC∥EF;同位角相等,两直线平行;两直线平行,内错角相等
31.(1)解:∵,
∴,
∵,
∴,
∴
(2)解:∵,∴,
∵,
∴,
∵,
∴,
∴
32.(1)证明:,
.
,
∠A=∠BFD.
.
(2)解:,
.
,
.
,,
.
(1)根据二直线平行,同位角相等,可得,结合已知推出∠A=∠BFD,从而由同位角相等,两直线平行,即可得出结论;
(2)根据二直线平行,同位角相等,可得,,再由平角的定义及已知可求出答案.
33.证明:∵∠A=∠D∴DE∥AB
∵∠B=∠BCF
∴AB∥CF
∴DE∥CF
本题考查了平行线的判定方法,由∠D=∠A,∠B=∠FCB,利用内错角相等两直线平行可,得到ED∥AB,AB∥CF,再由平行于同一条直线的两直线平行,得到ED∥CF,即可得证.
34.证明:
(两直线平行,内错角相等)
平分
又
.(同位角相等,两直线平行)
35.垂线的定义;;两直线平行,内错角相等;
36.(1)
(2)
37.(1)垂直的定义;等式的性质;;内错角相等,两直线平行;(2)对顶角相等;;等量代换;同位角相等,两直线平行.
38.(1)证明:∵,,
∴,
∴,
∴,
∵,
∴,
∴;
(2)解:∵,
又∵平分,
∴
∵,
∴.
(1)先根据同位角相等,两直线平行得到,可以得到,再根据等量代换得到即可得到结论;
(2)根据角平分线定义得到,然后再根据两直线平行,同位角相等解题.
(1)证明:∵,,
∴,
∴,
∴,
∵,
∴,
∴;
(2)解:∵,
又∵平分,
∴
∵,
∴.
39.两直线平行,内错角相等;等量代换;;;同位角相等,两直线平行;;;两直线平行,同旁内角互补;;两直线平行,同旁内角互补.
40.(1)解:过点E作,
∵,
∴,
∴,
∵,
∴;
(2)证明:过点E作,
∵,
∴,
∴,
∵,
∴;
(3)证明:延长和反向延长相交于点G,
∵,
∴,
∵,
∴,
∴,
∴.
(1)过点E作,得到,得出,结合,即可求解;
(2)过点E作,得到,得出,结合,即可求解;
(3)延长和反向延长相交于点G,由,得到,根据,得到,结合同位角相等,两直线平行,证得,再根据平行线性质,即可证得,
(1)解:过点E作,
∵,
∴,
∴,
∵,
∴;
(2)证明:过点E作,
∵,
∴,
∴,
∵,
∴;
(3)证明:延长和反向延长相交于点G,
∵,
∴,
∵,
∴,
∴,
∴.
41.(1)解:,理由如下:
∵,
∴,即,
∵,
∴,
∴;
(2)∵,
∴,
∴.
∵∠BAC=2∠CAD,,
∠BAE=∠BAC+∠CAD+∠EAD=5∠CAD.
∴∠CAD=23°,∠EAD=46°.
∵,
∴∠D=∠EAD=46°.
(1)根据角的和差关系得到,再根据平行线性质得,即可解答;
(2)由平行线的性质求得∠BAE的度数,由根据角的和差关系得 ∠BAC=2∠CAD,,即可求出∠CAD,最后再根据平行线的性质即可得到∠D的度数.
42.已知;;角平分线的定义;;等量代换;;;同位角相等,两直线平行
43.;两直线平行,同旁内角互补;;;;内错角相等,两直线平行
44.CD;同旁内角互补,两直线平行;∠AEF;两直线平行,内错角相等;∠EFH;GE;内错角相等,两直线平行;两直线平行,内错角相等.
期中真题专项复习 04 证明题
一、证明题
1.(2024七下·慈溪期中)如图,在四边形中,,.
(1)求的度数;
(2)若平分交于点,,求证:.
2.(2024七下·义乌期中)如图,D是BC上一点,DE∥AB,交AC于点E,F是AB上一点,且∠DEC+∠AFD=180°.
(1)求证:DF∥AC;
(2)若∠B+∠C=130°,求∠FDE的度数.
3.(2024七下·嘉善期中)如图,D,E分别在的边、上,F在线段上,且,.求证:.
4.(2024七下·拱墅期中)如图,在三角形中,D,E,F分别是上的点,且.
(1)若,试判断与是否垂直,并说明理由;
(2)若平分,,求的度数.
5.(2024七下·西湖期中)已知:点E在线段间(如图1).连接..
(1)求证:.
(2)如图2,点F在点E右侧.连接.
求证.
(3)如图3在(2)的条件下,线段,的延长线交于点H.交于点K.当平分,平分,,时,求的度数.
6.(2024七下·澄城期中)已知,如图,,,求证:,请完成解答过程.
证明:(已知)
▲ ( )
又(已知)
▲ ( )
▲ (两直线平行,内错角相等)
(等量代换)
7.(2024七下·子洲期中)如图,已知点A,B,D在一条直线上,,∠1=∠2,请填写∠B=∠C的理由.
解:因为,所以∠1= ▲ ( ),
∠2= ▲ ( ).
2因为∠1=∠2,所以∠B=∠C( ).
8.(2024七下·潮州期中)如图,已知点P在CD上,∠BAP+∠APD=180°,∠1=∠2,求证:∠E=∠F.
9.(2024七下·凉州期中)如图,若,,那么吗?请在下面的解答过程中填空或在括号内填写理由.
解:理由如下:
(已知),
____________(______),
______(______)
又(已知),
______(______)
(______).
10.(2024七下·福田期中)请将下列说理过程补充完整:
如图:,,,试说明.
解:因为(已知),
所以(______),
因为(已知),
所以______(两直线平行,内错角相等),
因为(已知),
所以_____________(______),
即,
所以(______).
11.(2024七下·上海市期中)如图,如图,已知,,,求的度数.
12.(2024七下·北京市期中)如图,,,求证.完成下面的证明过程.
证明:∵,,
∴(同角的补角相等).
∴ (内错角相等,两直线平行).
∴( ).
又∵(已知),
∴ (等量代换)﹒
∴( ).
∴(两直线平行,同位角相等).
13.(2024七下·柳州期中)如图,已知∠1=∠2,∠B=∠C,求证:AB∥CD.
14.(2024七下·镇海区期中)如图,已知F,E分别是射线上的点.连接,其中平分,平分,.
(1)试说明;
(2)若,求的度数.
15.(2024七下·惠阳期中)如图,已知AB∥CD,∠B+∠D=180°.求证:BC∥ED.
16.(2024七下·广州期中) 如图,已知,,垂足分别为D、F,,试说明:.请补充说明过程,并在括号内填上相应的理由.
解:,(已知),
( ),
( ).
( )
(已知).
( ).
∴ ( )
( ).
17.(2024七下·宜春期中)如图,已知,.求证:.请完善证明过程,并在括号内填上相应依据.
证明:∵(已知),
∴ ( ).
又∵(已知),
∴ ( ),
∴ ( ),
∴(两直线平行,同位角相等).
18.(2024七下·霞浦期中)填空:把下面的推理过程补充完整,并在括号内注明理由.
如图,已知BC分别交AB、DE于点B、C,且∠ABC+∠ECB=180°,∠P=∠Q.求证:∠1=∠2.
证明:因为∠ABC+∠ECB=180°(已知),
所以AB∥DE( ).
所以∠ABC=∠BCD( ).
因为∠P=∠Q(已知),
所以PB∥CQ( ).
所以∠PBC=( )(两直线平行,内错角相等).
因为∠1=∠ABC﹣( ),
∠2=∠BCD﹣( ),
所以∠1=∠2(等量代换).
19.(2024七下·黄埔期中)根据解答过程填空(理由或数学式).
已知:如图,,,求证:.
证明:∵(邻补角定义),
又∵(已知),
∴( ),
∴( ),
∴( )
∵(已知),
∴( ),
∴( ),
∴( ).
20.(2024七下·清城期中)如图,在三角形中,,垂足为,为上的点,,垂足为,点在上,连接,若,求证:.
21.(2024七下·天津市期中)如图,已知,,,垂足为A,请在横线上补全求的度数的解题过程或依据.
解:∵(已知).
∴ ( ).
∵已知),
∴ (等量代换).
∴
∴ (两直线平行,同旁内角互补).
又∵(已知),
∴ ( ).
∴ (等式的性质).
22.(2024七下·东昌府期中)如图,直线AB、CD相交于点O,OM⊥AB.
(1)若∠1=∠2,证明:ON⊥CD;(2)若∠1=∠BOC,求∠BOD的度数.
23.(2024七下·永州期中)填空:如图,在四边形中,分别于相交于点E、F.,,试说明.
解:∵,
∴____________.(______),
又∵,
∴____________(______),
∴____________(______).
24.(2024七下·澄海期中)如图,已知,,平分,平分,,求证:
请将下列证明过程中的空格补充完整
证明:∵,
( )
平分,平分
( )
=
( )
(两直线平行,内错角相等)
即( )
25.(2024七下·西城期中)已知:如图,,,.求证:平分.
证明:∵,,
∴,(_______).
∴.
∴__________(_______).
∴(_________).
(_________).
又∵,∴(等量代换).
∴平分.
26.(2024七下·北京市期中)请你补全证明过程或推理依据:
已知:如图,四边形,点E、F分别在边两方的延长线上,连接,若,.
求证:.
证明:∵点E在的延长线上(已知)
∴
又∵(已知)
∴ ( )
又∵(已知)
∴ ( )
∴( )
∴( )
27.(2024七下·西工期中)已知:如图所示,,和分别平分和,.求证:.
证明:∵和分别平分和(已知)
∴ ,
.( )
又∵(已知),
∴∠ (等量代换).
又∵(已知),
__________(等量代换),
∴( ).
28.(2024七下·滑县期中)如图,已知,,,将下面“求证:”的过程补充完整.
证明:∵,
∴,(判定依据:________,两直线平行)
∴________(两直线平行,内错角相等)
又∵,
∴________=________(等量代换),
∴________(判定依据:________,两直线平行)
又∵,
∴________°,(垂直的定义)
∴________°,(两直线平行,________)
∴.
29.(2024七下·龙口期中)如图,已知,,求证:.
下面是小明同学不完整的证明过程,请你在横线上补充完整,并在括号里填上每一步的推理依据.
证明:∵(已知),
∴_________,
∵(_________),
∴(_________),
∴(_________),
∴_________(两直线平行,同旁内角互补),
∵(_________),
∴(_________).
30.(2024七下·北京市期中)完成下面的证明.已知:如图,AC⊥BD,EF⊥BD,∠A=∠1.求证:EF平分∠BED.
证明:∵AC⊥BD,EF⊥BD,
∴∠ACB=90°,∠EFB=90°.(______)
∴∠ACB=∠EFB.
∴_____________.(______)
∴∠A=∠2.(两直线平行,同位角相等)
∠3=∠1.(_______)
又∵∠A=∠1,
∴∠2=∠3.
∴EF平分∠BED.
31.(2024七下·鄞州期中)如图,在三角形中,点D在上,交于点E,点F在,.
(1)试说明:;
(2)若,求的度数.
32.(2024七下·杭州期中)如图,点是上一点,,交于点,且.
(1)求证:;
(2)若,求的度数(用含的代数式表示).
33.(2024七下·高州期中)已知:如图,∠D=∠A,∠B=∠FCB
求证:ED//CF
34.(2024七下·白云期中)如图,AD∥BE,AE平分∠BAD,CD与AE相交于F,∠CFE=∠E.求证:AB∥CD.
35.(2024七下·厦门期中)请在下列空格内填写结论或理由,完成推理过程.
如图,于D,点E在的延长线上,于G,交于点F,.
求证:平分.
证明:∵于D,于G(已知)
∴(______)
∴______(同位角相等,两直线平行)
∴(______)
______(两直线平行,同位角相等)
又∵(已知)
∴(等量代换)
∴平分(角平分线的定义)
36.(2024七下·瓜州期中)如图,已知平分交于点E.
(1)试说明:与的关系
(2)若于点,求的度数.
37.(2024七下·滨海期中)(1)已知:如图,且,求证.
证明:∵,(已知),
∴(______),
∵(已知)
∵(______),
∴______,
∴(______);
(2)已知:如图,直线,被所截,,求证:.
证明:∵(______),
又∵(已知),
∴______(______),
∴(______).
38.(2024七下·余姚期中)如图,于点D,点F是上任意一点,过点F作于点E,且.
(1)求证:;
(2)若,平分,求的度数.
39.(2024七下·柘城期中)中国汉字博大精深,方块文字智慧灵秀,奥妙无穷.如图(1)是一个“互”字,如图2是由图1抽象出的几何图形,其中,,点,,在同一直线上,点,,在同一直线上,且.
求证:.
证明∶如图,延长交于点.
∵(已知),
∴(_________)
又∵(已知),
∴(________)
∴____________(________)
∴_______+_______(_______)
∵(已知),
∴_______(__________)
∴.
40.(2024七下·凉州期中)先阅读再解答:
(1)如图1,,试说明:;
(2)已知:如图2,,求证:;
(3)已知:如图3,,.求证:.
41.(2024七下·滨江期中)如图,在中,点C是边上一点,点E是外一点,连结,使得,且.
(1)与相等吗?请说明理由;
(2)若,,求的度数.
42.(2024七下·滨海期中)如图所示,已知,平分,平分,,试说明:.
解:(______),
又平分,
______(______),
又平分,
______,
.(______)
,
____________
(______)
43.(2024七下·清苑期中)如图,点D,E是线段上的点,点F是线段上的点,,点H是上的点,且.求证:.
请将下面的证明过程补充完整:
证明:∵,
∴______.(理由:_________)
∵,
∴_____.
∴____________.(理由:______)
∴.
44.(2024七下·蕲春期中)填空,完成下列证明过程,并在括号中注明理由.
如图,已知∠BEF+∠EFD=180°,∠AEG=∠HFD,求证:∠G=∠H.
解:∵∠BEF+∠EFD=180°,(已知).
∴AB// ( ).
∴ =∠EFD( ).
又∵∠AEG=∠HFD,
∴∠AEF﹣∠AEG=∠EFD﹣∠HFD,即∠GEF= .
∴ //FH( ).
∴∠G=∠H.( ).
答案解析部分
1.(1)解:解:,
,
,
,
的度数是110°;
(2)证明:∵平分交于点,=110°,
,
,
,
,
,
.
(1)根据平行线的性质得,最后进行计算即可求出答案;
(2)根据角平分线的定义求出∠DAE=55°,再根据平行线的性质得∠AEB=∠DAE=55°,从而得∠AEB=∠BCD,最后根据平行线的判定得AE∥CD.
2.(1)证明:∵,
∴,
∵,
∴,
∴;
(2)解:∵,
∴,
根据(1)可知:,,
∵,
∴,
∵,
∴.
(1)根据平行线的性质得到,进而结合题意得到,再根据平行线的判定即可求解;
(2)先根据题意得到,进而根据(1)可知:,,从而根据平行线的性质即可求解。
3.证明:∵,,
∴,
∴,
∴,
∵,
∴,
∴.
先证明,可得,于是根据平行线的性质可得,再根据平行线性质得,等量代换即可证明结论.
4.(1)解:,理由如下:
,
,
∴∠BFD=∠FDE.
,
,
,
.
(2)解:平分,
,
,
,∠AFE=∠FED.
∵△FDE中,∠FDE+∠DFE+∠FED=2∠FDE+∠AFE=180°,
又∵∠FDE+3∠AFE=180°,
∴2∠FDE+∠AFE=∠FDE+3∠AFE,即∠FDE=2∠AFE.
∴5∠AFE=180°,
解得:∠AFE=36°,
∴∠BFE=2∠FDE=4∠AFE=144°.
5.(1)解:如图,过点E作,
∴,
∴,
∵,
∴,
∴,
∴;
(2)解:如图,过点F作,
∵,
∴,
∴,
∴,
即;
(3)解:设,∵平分,平分,
∴,
∴,
由(1)得:,
∵,
∴,
∵,
∴,
∴,
∴,
∴,
∴,
∵,
∴,
解得:,
∴,
∴.
6.证明:∵AD∥BE(已知)
∴∠A=∠3,(两直线平行,同位角相等)
又∵∠1=∠2(已知)
∴AC∥DE( 内错角相等,两直线平行)
∴∠3=∠E(两直线平行,内错角相等)
∴∠A=∠E(等量代换)
故答案为:3,两直线平行,同位角相等;DE,内错角相等,两直线平行;E
通过对已知的观察分析可以看出,由两直线平行,同位角相等可以得到∠A=∠3,再由内错角相等,两直线平行,推出AC∥DE,进而由 两直线平行,内错角相等 得到∠3=∠E,最后由等量代换得∠A=∠E.
7.因为,所以∠1=∠B(两直线平行,同位角相等),
∠2=∠C(两直线平行,内错角相等).
因为∠1=∠2,所以∠B=∠C(等量代换).
利用平行线的性质求出∠1=∠B和∠2=∠C,通过等量转化即可推出 ∠B=∠C .
8.证明:∵∠BAP+∠APD=180°,(已知)
∴AB∥CD.(同旁内角互补,两直线平行)
∴∠BAP=∠CPA.(两直线平行,内错角相等)
∵∠1=∠2,(已知)
∴∠BAP-∠1=∠CPA-∠2
∴∠EAP=∠FPA.
∴AE∥PF.(内错角相等,两直线平行)
∴∠E=∠F.(两直线平行,内错角相等)
利用同旁内角互补,两直线平行可证得AB∥CD,利用平行线的性质可推出∠BAP=∠CPA,结合已知条件可证得∠EAP=∠FPA;再利用内错角相等,两直线平行可证得AE∥PF,然后利用平行线的性质可证得结论.
9.;;内错角相等,两直线平行;;两直线平行,内错角相等;;等量代换;同位角相等,两直线平行.
10.两直线平行,内错角相等;;,;等式的性质;等量代换
11.
12.,两直线平行,内错角相等,,同位角相等,两直线平行
13.解:∵∠1=∠2(已知),∠1=∠4(对顶角相等)
∴∠2=∠4(等量代换)
∴EC∥BF(同位角相等,两直线平行)
∴∠C=∠3(两直线平行,同位角相等)
又∵∠B=∠C(已知)
∵∠B=∠3(等量代换)
∴AB∥CD(内错角相等,两直线平行)
根据对顶角相等,得到∠1=∠4,得到∠2=∠4,由EC∥BF,得到∠C=∠3,根据∠B=∠C,得出∠B=∠3,结合内错角相等,两直线平行,即可证得AB∥CD.
14.(1)解:如图,,
平分,
,
,
(2)解:如图
,
,
,
,
平分,
,
,
,
,
,
,
的度数为
(1)根据等边对等角得到,根据角平分线得到,即可得到,再根据平行线的判定定理得到结论即可;
(2)先得到,再根据两直线平行,内错角相等得到,根据角平分线的定义得到,求出∠3的度数,即可得到的度数解题.
15.证明:∵,
∴,
∵,
∴,
∴.
由两直线平行,内错角相等可得∠B=∠C,由等量代换可得∠C+∠D=180°,然后根据“同旁内角互补,两直线平行”可求解.
16.垂直的定义;同位角相等,两直线平行;;两直线平行,同旁内角互补;同角的补角相等;;内错角相等,两直线平行;两直线平行,同位角相等
解:,(已知),
( 垂直的定义 ),
( 同位角相等,两直线平行 ).
∠1( 两直线平行,同旁内角互补 )
(已知).
( 同角的补角相等 ).
∴DG( 内错角相等,两直线平行 )
( 两直线平行,同位角相等 ).
根据垂直的定义得∠ADB=∠EFB=90°,由同位角相等,两直线平行,得AD∥EF,由二直线平行,同旁内角互补,得∠1+∠2=180°,结合已知,由同角的补角相等得∠1=∠3,由内错角相等,两直线平行,得AB∥DG,最后根据两直线平行,同位角相等可得∠GDC=∠B.
17.;两直线平行,内错角相等;;等量代换;;内错角相等,两直线平行
18.同旁内角互补,两直线平行;两直线平行,内错角相等;内错角相等,两直线平行;∠BCQ;∠PBC;∠BCQ
19.同角的补角相等;内错角相等,两直线平行;两直线平行,内错角相等;等量代换;同位角相等,两直线平行;两直线平行,同位角相等
20.证明:∵,,∴,
∴,
∴,
∴
∵,
∴,
∴,
∴.
本题考查平行线的判定与性质,根据,,得到,证得,结合,得到,结合内错角相等,两直线平行,证得,再由两直线平行,同位角相等,即可证得.
21.;两直线平行,内错角相等;;;;;垂直的定义;
22.(1)ON⊥CD.(2)60°.
23.1;2;两直线平行,内错角相等;2;3;两直线平行,同位角相等;1;3;等量代换.
24.两直线平行,同位角相等;角平分线的定义;;同位角相等,两直线平行;;垂直的定义.
25.垂线的定义;;同旁内角互补,两直线平行;两直线平行,同位角相等;两直线平行,内错角相等;
26.1;1;同角的补角相等;3;等量代换;内错角相等,两直线平行;两直线平行,内错角相等
27.角平分线的定义;;同位角相等,两直线平行
28.同位角相等;内错角相等;90;90;同位角相等
29.;已知;等量代换;同位角相等,两直线平行;;对顶角相等;等量代换
30.垂直定义;AC∥EF;同位角相等,两直线平行;两直线平行,内错角相等
31.(1)解:∵,
∴,
∵,
∴,
∴
(2)解:∵,∴,
∵,
∴,
∵,
∴,
∴
32.(1)证明:,
.
,
∠A=∠BFD.
.
(2)解:,
.
,
.
,,
.
(1)根据二直线平行,同位角相等,可得,结合已知推出∠A=∠BFD,从而由同位角相等,两直线平行,即可得出结论;
(2)根据二直线平行,同位角相等,可得,,再由平角的定义及已知可求出答案.
33.证明:∵∠A=∠D∴DE∥AB
∵∠B=∠BCF
∴AB∥CF
∴DE∥CF
本题考查了平行线的判定方法,由∠D=∠A,∠B=∠FCB,利用内错角相等两直线平行可,得到ED∥AB,AB∥CF,再由平行于同一条直线的两直线平行,得到ED∥CF,即可得证.
34.证明:
(两直线平行,内错角相等)
平分
又
.(同位角相等,两直线平行)
35.垂线的定义;;两直线平行,内错角相等;
36.(1)
(2)
37.(1)垂直的定义;等式的性质;;内错角相等,两直线平行;(2)对顶角相等;;等量代换;同位角相等,两直线平行.
38.(1)证明:∵,,
∴,
∴,
∴,
∵,
∴,
∴;
(2)解:∵,
又∵平分,
∴
∵,
∴.
(1)先根据同位角相等,两直线平行得到,可以得到,再根据等量代换得到即可得到结论;
(2)根据角平分线定义得到,然后再根据两直线平行,同位角相等解题.
(1)证明:∵,,
∴,
∴,
∴,
∵,
∴,
∴;
(2)解:∵,
又∵平分,
∴
∵,
∴.
39.两直线平行,内错角相等;等量代换;;;同位角相等,两直线平行;;;两直线平行,同旁内角互补;;两直线平行,同旁内角互补.
40.(1)解:过点E作,
∵,
∴,
∴,
∵,
∴;
(2)证明:过点E作,
∵,
∴,
∴,
∵,
∴;
(3)证明:延长和反向延长相交于点G,
∵,
∴,
∵,
∴,
∴,
∴.
(1)过点E作,得到,得出,结合,即可求解;
(2)过点E作,得到,得出,结合,即可求解;
(3)延长和反向延长相交于点G,由,得到,根据,得到,结合同位角相等,两直线平行,证得,再根据平行线性质,即可证得,
(1)解:过点E作,
∵,
∴,
∴,
∵,
∴;
(2)证明:过点E作,
∵,
∴,
∴,
∵,
∴;
(3)证明:延长和反向延长相交于点G,
∵,
∴,
∵,
∴,
∴,
∴.
41.(1)解:,理由如下:
∵,
∴,即,
∵,
∴,
∴;
(2)∵,
∴,
∴.
∵∠BAC=2∠CAD,,
∠BAE=∠BAC+∠CAD+∠EAD=5∠CAD.
∴∠CAD=23°,∠EAD=46°.
∵,
∴∠D=∠EAD=46°.
(1)根据角的和差关系得到,再根据平行线性质得,即可解答;
(2)由平行线的性质求得∠BAE的度数,由根据角的和差关系得 ∠BAC=2∠CAD,,即可求出∠CAD,最后再根据平行线的性质即可得到∠D的度数.
42.已知;;角平分线的定义;;等量代换;;;同位角相等,两直线平行
43.;两直线平行,同旁内角互补;;;;内错角相等,两直线平行
44.CD;同旁内角互补,两直线平行;∠AEF;两直线平行,内错角相等;∠EFH;GE;内错角相等,两直线平行;两直线平行,内错角相等.
同课章节目录
