北京市人大附朝阳学校2024~2025学年初三下三月数学考试卷(图片版,无答案)
文档属性
| 名称 | 北京市人大附朝阳学校2024~2025学年初三下三月数学考试卷(图片版,无答案) |
|
|
| 格式 | |||
| 文件大小 | 793.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-03-29 13:30:52 | ||
图片预览



文档简介
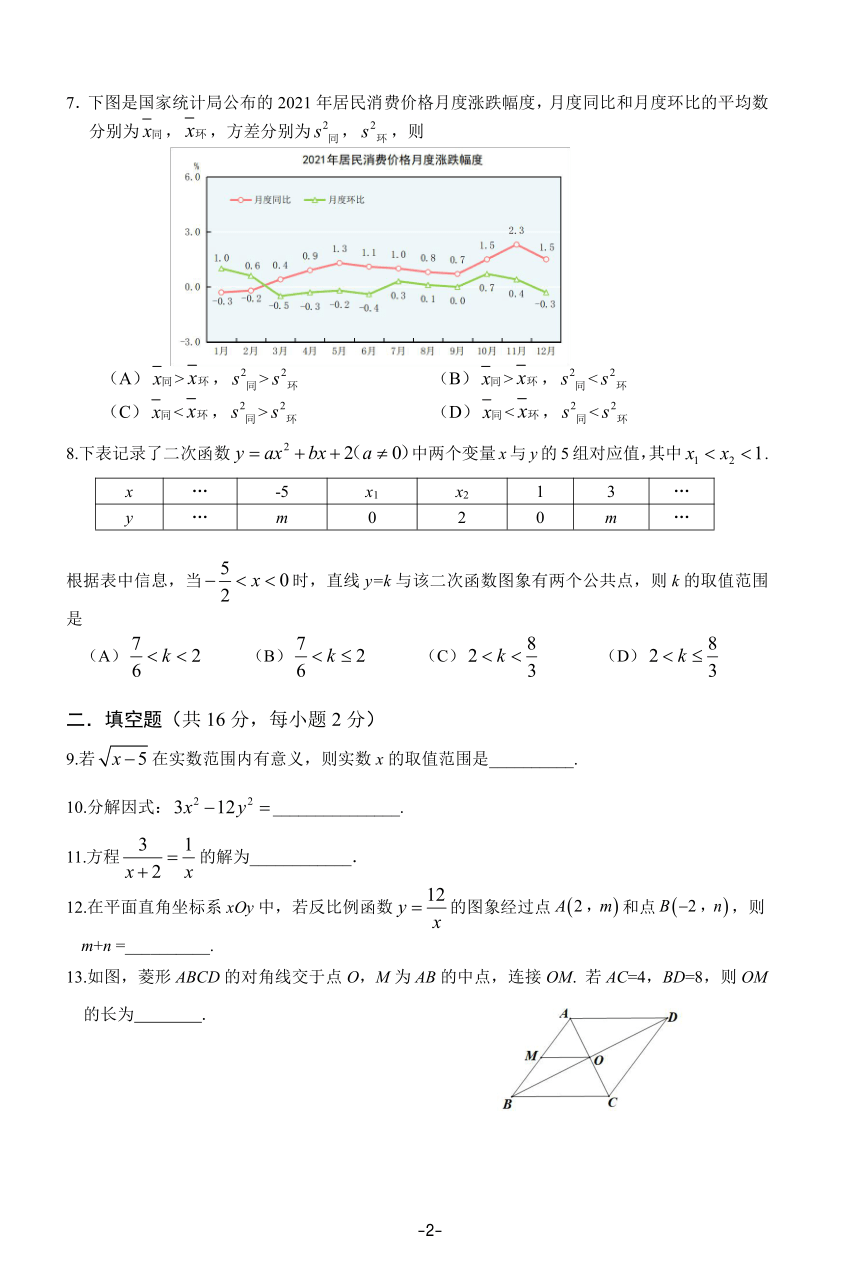
人大附中朝阳学校九年级数学质量检测(四)
(时间: 120 分钟 满分:100 分)
一.选择题(共 16分,每小题 2分)
1.下列立体图形中,主视图是圆的是
(A) (B) (C) (D)
2. 2024年 5月 3 日,我国嫦娥六号顺利发射飞向太空,随后历时五天抵达第四阶段,进行环月
飞行任务. 6 月 2 号早上嫦娥六号在月球背面的南极-艾特肯盆地成功落月,月球距离地球约
384000千米,将 384 000 000用科学记数法表示为
(A)38.4×107 (B)3.84×108 (C)3.84×109 (D)0.384×109
3.不透明的袋子中装有 2个红球和 3个黄球,两种球除颜色外无其他差别,从中随机摸出一个小
球,摸到黄球的概率是
2 3 2 3
(A) (B) (C) (D)
3 4 5 5
4. 如图,点 O在直线 AB上,OC⊥OD.若∠AOC=120°,则∠BOD的度数为
(A)30 (B)40° (C)50° (D)60°
5.已知关于 x 的一元二次方程 x2 2x a 0有两个相等的实数根,则实数 a的值是
(A) 1 (B)0 (C)1 (D)2
6.如图,点 O为线段 AB的中点,∠ACB=∠ADB=90°,连接 OC,OD. 则下列结论不一定成立
的是
(A)OC=OD (B)∠BDC=∠BAC
(C)∠BCD+∠BAD=180° (D)AC平分∠BAD
-1-
班级: 姓名: 考号:
7.下图是国家统计局公布的 2021年居民消费价格月度涨跌幅度,月度同比和月度环比的平均数
分别为 x 2 2同, x环,方差分别为 s ,同 s 环,则
(A) x > x s2 > s2 B) x > x s2 < s2同 环, 同 环 ( 同 环, 同 环
(C) x < x s2 > s2同 环, 同 环 (D) x同< x
2
环, s 同< s
2
环
8. 2下表记录了二次函数 y ax bx (2 a 0)中两个变量 x与 y的 5组对应值,其中 x1 x2 1.
x … -5 x1 x2 1 3 …
y … m 0 2 0 m …
5
根据表中信息,当 x 0时,直线 y=k与该二次函数图象有两个公共点,则 k的取值范围
2
是
7 7
(A) k 2 (B) k 2 8 8 (C) 2 k (D) 2 k
6 6 3 3
二.填空题(共 16分,每小题 2分)
9.若 x 5在实数范围内有意义,则实数 x的取值范围是__________.
10.分解因式:3x2 12y2 _______________.
3 1
11.方程 的解为____________.
x 2 x
12
12.在平面直角坐标系 xOy中,若反比例函数 y 的图象经过点 A 2,m 和点 B 2,n ,则
x
m+n =__________.
13.如图,菱形 ABCD的对角线交于点 O,M为 AB的中点,连接 OM. 若 AC=4,BD=8,则 OM
的长为 .
-2-
班级: 姓名: 考号:
14.如图,AB是⊙O的直径,CD是弦,连接 AC,AD.若∠BAC=40°,则∠D= °.
15.用一组 a,b,m 的值说明“若 a b ,则ma mb ”是错误的,这组数可以是 a=______,
b=______.m=_______.
16.某跨学科综合实践小组准备购买一些盒子存放实验材料.现有 A,B,C三种型号的盒子,盒
子容量和单价如下表所示:
盒子型号 A B C
盒子容量/升 2 3 4
盒子单价/元 5 6 9
其中 A型号盒子做促销活动:购买三个及三个以上可一次性返现金 4元,现有 28升材料需
要存放且每个盒子要装满材料.
(1)若购买 A,B,C三种型号的盒子的个数分别为 2,4,3,则购买费用为 元;
(2)若一次性购买所需盒子且使购买费用不超过 58元,则购买 A,B,C三种型号的盒子
的个数分别为 .(写出一种即可)
三.解答题(共 68分)
17.计算:6cos45° 18 5 ( 2) 0 .
x 2 2x 1,
18.解不等式组: 3x 5
x. 2
19.已知 x2 x 3 0,求代数式 (x 2)(x 2) x(2 x)的值.
-3-
20.如图,在△ABC中,AB=AC.
(1)使用直尺和圆规,作 AD⊥BC交 BC于点 D(保留作图痕迹);
(2)以 D为圆心,DC的长为半径作弧,交 AC于点 E,连接 BE,DE.
①∠BEC= °;
②写出图中一.个.与∠CBE相等的角 .
21.如图,在四边形 ABCD中,∠ACB=∠CAD=90°,点 E在 BC上,AE∥DC,EF⊥AB,垂足
为点 F.
(1)求证:四边形 AECD是平行四边形;
4
(2)若 AE平分∠BAC,BE=5, cosB ,求 BF和 AD的长.
5
22.在平面直角坐标系 xOy中,一次函数 y=kx+b(k≠0)的图象经过点(0,1),(-2,2),与 x
轴交于点 A.
(1)求该一次函数的表达式及点 A的坐标;
(2)当 x>2时,对于 x的每一个值,函数 y=2x+m的值大于一次函数 y=kx+b(k≠0)的值,
直接写出 m的取值范围.
23.列方程解应用题
无人配送以其高效、安全、低成本等优势,正在成为物流运输行业的新趋势.某物流园区
使用 1 辆无人配送车平均每天配送的包裹数量是 1 名快递员平均每天配送包裹数量的 5 倍.要
配送 6 000 件包裹,使用 1 辆无人配送车所需时间比 4 名快递员同时配送所需时间少 2 天,求
1名快递员平均每天可配送包裹多少件?
-4-
24.如图,AB是⊙O的直径,C,D是⊙O上的点且 ,,过点 D作 DE⊥AC交 AC的延
长线于点 E.
(1)求证:DE是⊙O的切线;
(2)连接 CD,若 cos ECD 7 ,AB=15,求 CD的长.
5
25.某公园内人工湖上有一座拱桥(横截面如图所示),跨度 AB为 4米.在距点 A水平距离为 d
米的地点,拱桥距离水面的高度为 h米.小红根据学习函数的经验,对 d和 h之间的关系进
行了探究.
下面是小红的探究过程,请补充完整:
(1)经过测量,得出了 d和 h的几组对应值,如下表.
d(米) 0 0.6 1 1.8 2.4 3 3.6 4
h(米) 0.88 1.90 2.38 2.86 2.80 2.38 1.60 0.88
在 d和 h这两个变量中,________是自变量,________是这个变量的函数;
(2) 在下面的平面直角坐标系 xOy中,画出(1)中所确定的函数的图象;
-5-
班级: 姓名: 考号:
(3) 结合表格数据和函数图象,解决问题:
①桥墩露出水面的高度 AE为 米;
②现公园欲开设游船项目,现有长为 3.5米,宽为 1.5米,露出水面高度为 2米的游船.为安
全起见,公园要在水面上的 C、D两处设置警戒线,并且 CE=DF,要求游船能从 C,D两点之
间安全通过.则 C距桥墩的距离 CE至少为 米.(精确到 0.1米)
26.在平面直角坐标系 xOy 中,点(m+2,y1),(6,y2)为抛物线 y=x2-2mx+n 上两个不同的点.
(1)求抛物线的对称轴(用含 m 的式子表示);
(2)若 y1<n<y2,求 m 的取值范围.
-6-
班级: 姓名: 考号:
27.如图,四边形 ABCD是正方形,以点 A为中心,将线段 AB顺时针旋转α(0°<α<90°),
得到线段 AE,连接 DE,BE.
(1)求∠DEB的度数;
(2)过点 B作 BF⊥DE于点 F,连接 CF,依题意补全图形,用等式表示线段 DE与 CF之间
的数量关系,并证明.
-7-
28.在平面直角坐标系 xOy中,⊙O的半径为 1,点 P是⊙O外一点,给出如下定义:若在⊙O
上存在点 T,使得点 P关于某条过点 T的直线对称后的点 Q在⊙O上,则称点 Q为点 P关于
⊙O的“关联对称点”.
(1)若点 P在直线 y=2x上;
2 2
1 若点 P的坐标为(1,2),则 Q1(0,1),Q2(1,0),Q3( , )中,是点 P
2 2
关于⊙O的“关联对称点”的是____________;
2 若存在点 P关于⊙O的“关联对称点”,求点 P的横坐标 xP 的取值范围;
3
(2)已知点 A(2, ),动点 M满足 AM≤1,若点 M关于⊙O的“关联对称点”N存在,直
2
接写出 MN的取值范围.
-8-
(时间: 120 分钟 满分:100 分)
一.选择题(共 16分,每小题 2分)
1.下列立体图形中,主视图是圆的是
(A) (B) (C) (D)
2. 2024年 5月 3 日,我国嫦娥六号顺利发射飞向太空,随后历时五天抵达第四阶段,进行环月
飞行任务. 6 月 2 号早上嫦娥六号在月球背面的南极-艾特肯盆地成功落月,月球距离地球约
384000千米,将 384 000 000用科学记数法表示为
(A)38.4×107 (B)3.84×108 (C)3.84×109 (D)0.384×109
3.不透明的袋子中装有 2个红球和 3个黄球,两种球除颜色外无其他差别,从中随机摸出一个小
球,摸到黄球的概率是
2 3 2 3
(A) (B) (C) (D)
3 4 5 5
4. 如图,点 O在直线 AB上,OC⊥OD.若∠AOC=120°,则∠BOD的度数为
(A)30 (B)40° (C)50° (D)60°
5.已知关于 x 的一元二次方程 x2 2x a 0有两个相等的实数根,则实数 a的值是
(A) 1 (B)0 (C)1 (D)2
6.如图,点 O为线段 AB的中点,∠ACB=∠ADB=90°,连接 OC,OD. 则下列结论不一定成立
的是
(A)OC=OD (B)∠BDC=∠BAC
(C)∠BCD+∠BAD=180° (D)AC平分∠BAD
-1-
班级: 姓名: 考号:
7.下图是国家统计局公布的 2021年居民消费价格月度涨跌幅度,月度同比和月度环比的平均数
分别为 x 2 2同, x环,方差分别为 s ,同 s 环,则
(A) x > x s2 > s2 B) x > x s2 < s2同 环, 同 环 ( 同 环, 同 环
(C) x < x s2 > s2同 环, 同 环 (D) x同< x
2
环, s 同< s
2
环
8. 2下表记录了二次函数 y ax bx (2 a 0)中两个变量 x与 y的 5组对应值,其中 x1 x2 1.
x … -5 x1 x2 1 3 …
y … m 0 2 0 m …
5
根据表中信息,当 x 0时,直线 y=k与该二次函数图象有两个公共点,则 k的取值范围
2
是
7 7
(A) k 2 (B) k 2 8 8 (C) 2 k (D) 2 k
6 6 3 3
二.填空题(共 16分,每小题 2分)
9.若 x 5在实数范围内有意义,则实数 x的取值范围是__________.
10.分解因式:3x2 12y2 _______________.
3 1
11.方程 的解为____________.
x 2 x
12
12.在平面直角坐标系 xOy中,若反比例函数 y 的图象经过点 A 2,m 和点 B 2,n ,则
x
m+n =__________.
13.如图,菱形 ABCD的对角线交于点 O,M为 AB的中点,连接 OM. 若 AC=4,BD=8,则 OM
的长为 .
-2-
班级: 姓名: 考号:
14.如图,AB是⊙O的直径,CD是弦,连接 AC,AD.若∠BAC=40°,则∠D= °.
15.用一组 a,b,m 的值说明“若 a b ,则ma mb ”是错误的,这组数可以是 a=______,
b=______.m=_______.
16.某跨学科综合实践小组准备购买一些盒子存放实验材料.现有 A,B,C三种型号的盒子,盒
子容量和单价如下表所示:
盒子型号 A B C
盒子容量/升 2 3 4
盒子单价/元 5 6 9
其中 A型号盒子做促销活动:购买三个及三个以上可一次性返现金 4元,现有 28升材料需
要存放且每个盒子要装满材料.
(1)若购买 A,B,C三种型号的盒子的个数分别为 2,4,3,则购买费用为 元;
(2)若一次性购买所需盒子且使购买费用不超过 58元,则购买 A,B,C三种型号的盒子
的个数分别为 .(写出一种即可)
三.解答题(共 68分)
17.计算:6cos45° 18 5 ( 2) 0 .
x 2 2x 1,
18.解不等式组: 3x 5
x. 2
19.已知 x2 x 3 0,求代数式 (x 2)(x 2) x(2 x)的值.
-3-
20.如图,在△ABC中,AB=AC.
(1)使用直尺和圆规,作 AD⊥BC交 BC于点 D(保留作图痕迹);
(2)以 D为圆心,DC的长为半径作弧,交 AC于点 E,连接 BE,DE.
①∠BEC= °;
②写出图中一.个.与∠CBE相等的角 .
21.如图,在四边形 ABCD中,∠ACB=∠CAD=90°,点 E在 BC上,AE∥DC,EF⊥AB,垂足
为点 F.
(1)求证:四边形 AECD是平行四边形;
4
(2)若 AE平分∠BAC,BE=5, cosB ,求 BF和 AD的长.
5
22.在平面直角坐标系 xOy中,一次函数 y=kx+b(k≠0)的图象经过点(0,1),(-2,2),与 x
轴交于点 A.
(1)求该一次函数的表达式及点 A的坐标;
(2)当 x>2时,对于 x的每一个值,函数 y=2x+m的值大于一次函数 y=kx+b(k≠0)的值,
直接写出 m的取值范围.
23.列方程解应用题
无人配送以其高效、安全、低成本等优势,正在成为物流运输行业的新趋势.某物流园区
使用 1 辆无人配送车平均每天配送的包裹数量是 1 名快递员平均每天配送包裹数量的 5 倍.要
配送 6 000 件包裹,使用 1 辆无人配送车所需时间比 4 名快递员同时配送所需时间少 2 天,求
1名快递员平均每天可配送包裹多少件?
-4-
24.如图,AB是⊙O的直径,C,D是⊙O上的点且 ,,过点 D作 DE⊥AC交 AC的延
长线于点 E.
(1)求证:DE是⊙O的切线;
(2)连接 CD,若 cos ECD 7 ,AB=15,求 CD的长.
5
25.某公园内人工湖上有一座拱桥(横截面如图所示),跨度 AB为 4米.在距点 A水平距离为 d
米的地点,拱桥距离水面的高度为 h米.小红根据学习函数的经验,对 d和 h之间的关系进
行了探究.
下面是小红的探究过程,请补充完整:
(1)经过测量,得出了 d和 h的几组对应值,如下表.
d(米) 0 0.6 1 1.8 2.4 3 3.6 4
h(米) 0.88 1.90 2.38 2.86 2.80 2.38 1.60 0.88
在 d和 h这两个变量中,________是自变量,________是这个变量的函数;
(2) 在下面的平面直角坐标系 xOy中,画出(1)中所确定的函数的图象;
-5-
班级: 姓名: 考号:
(3) 结合表格数据和函数图象,解决问题:
①桥墩露出水面的高度 AE为 米;
②现公园欲开设游船项目,现有长为 3.5米,宽为 1.5米,露出水面高度为 2米的游船.为安
全起见,公园要在水面上的 C、D两处设置警戒线,并且 CE=DF,要求游船能从 C,D两点之
间安全通过.则 C距桥墩的距离 CE至少为 米.(精确到 0.1米)
26.在平面直角坐标系 xOy 中,点(m+2,y1),(6,y2)为抛物线 y=x2-2mx+n 上两个不同的点.
(1)求抛物线的对称轴(用含 m 的式子表示);
(2)若 y1<n<y2,求 m 的取值范围.
-6-
班级: 姓名: 考号:
27.如图,四边形 ABCD是正方形,以点 A为中心,将线段 AB顺时针旋转α(0°<α<90°),
得到线段 AE,连接 DE,BE.
(1)求∠DEB的度数;
(2)过点 B作 BF⊥DE于点 F,连接 CF,依题意补全图形,用等式表示线段 DE与 CF之间
的数量关系,并证明.
-7-
28.在平面直角坐标系 xOy中,⊙O的半径为 1,点 P是⊙O外一点,给出如下定义:若在⊙O
上存在点 T,使得点 P关于某条过点 T的直线对称后的点 Q在⊙O上,则称点 Q为点 P关于
⊙O的“关联对称点”.
(1)若点 P在直线 y=2x上;
2 2
1 若点 P的坐标为(1,2),则 Q1(0,1),Q2(1,0),Q3( , )中,是点 P
2 2
关于⊙O的“关联对称点”的是____________;
2 若存在点 P关于⊙O的“关联对称点”,求点 P的横坐标 xP 的取值范围;
3
(2)已知点 A(2, ),动点 M满足 AM≤1,若点 M关于⊙O的“关联对称点”N存在,直
2
接写出 MN的取值范围.
-8-
同课章节目录
