中考数学复习专项突破重难题型二 课件(共16张PPT)
文档属性
| 名称 | 中考数学复习专项突破重难题型二 课件(共16张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 896.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-03-30 13:17:03 | ||
图片预览





文档简介
(共16张PPT)
重难题型二 多结论选填题
类型一:代数多结论选填题
如图,抛物线y=ax2+bx+c(a≠0)与x轴
交于点A,B,与y轴交于点C,对称轴为直线
x=-1.若点A的坐标为(-4,0),则下列结论中
正确的是 ( )
A.2a+b=0
B.4a-2b+c>0
C.x=2是关于x的一元二次方程ax2+bx+c=0(a≠0)的一个根
D.点(x1,y1),(x2,y2)在抛物线上,当x1>x2>-1时,y1<y2<0
C
【分层分析】∵对称轴为直线x=-1,∴b= ,∴2a-b= ,故可判断A,∵点A的坐标为(-4,0),∴当x=-2时,y=4a-2b+c< ,故可判断B,易得抛物线与x轴的另一个交点为 ,故可判断C,当X 时,y随x的增大而增大,∴当x1>x2>-1时,y1 y2,故可判断D.
2a
0
0
(2,0)
>-1
>
1.(2024·滁州模拟)如图,已知直线y=3x+b与y=ax-2的交点的横坐标为-2,根据图象,下列结论中错误的是 ( )
A.a>0
B.b>0
C.x=-2是方程3x+b=ax-2的解
D.x>-2是不等式ax-2>3x+b的解集
D
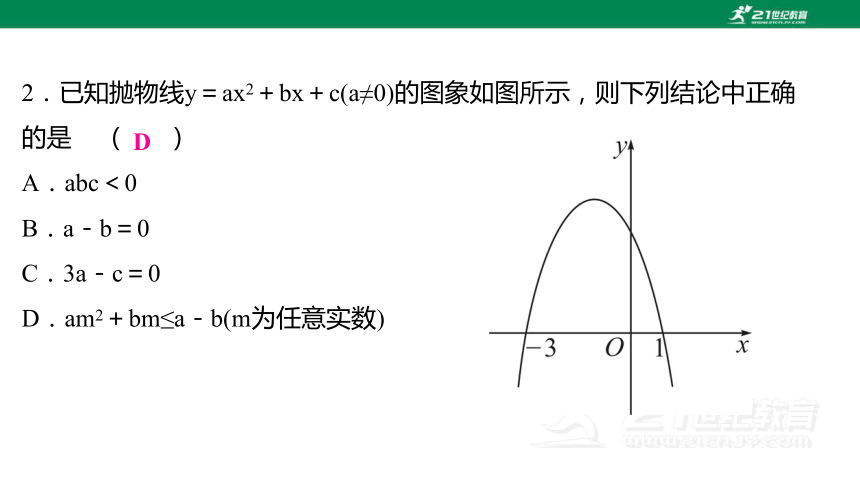
2.已知抛物线y=ax2+bx+c(a≠0)的图象如图所示,则下列结论中正确的是 ( )
A.abc<0
B.a-b=0
C.3a-c=0
D.am2+bm≤a-b(m为任意实数)
D
C
类型二:几何多结论选填题
(2024T8)
4.(2024·河北)如图,AD与BC交于点O,△ABO和△CDO关于直线PQ对称,点A,B的对称点分别是点C,D.下列结论中不一定正确的是( )
A.AD⊥BC B.AC⊥PQ
C.△ABO ≌△CDO D.AC∥BD
A
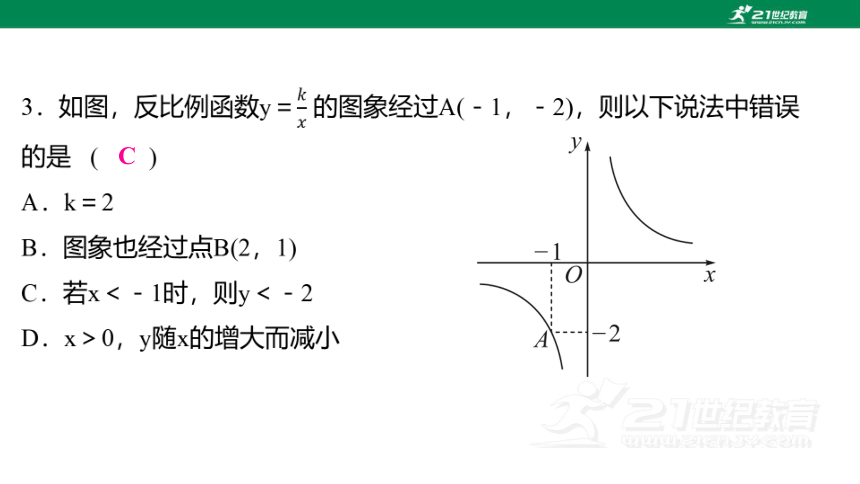
5.(2024·湖南)如图,在△ABC中,D,E分别为边AB,AC的中点.下列结论中错误的是 ( )
A.DE∥BC
B.△ADE∽△ABC
C.BC=2DE
D.S△ADE=S△ABC
D
6.(2023·苏州)如图,在正方形网格内,线段PQ的两个端点都在格点上,网格内另有A,B,C,D四个格点,下面四个结论中,正确的是 ( )
A.连接AB,则AB∥PQ
B.连接BC,则BC∥PQ
C.连接BD,则BD⊥PQ
D.连接AD,则AD⊥PQ
B
7.(2024·眉山)如图,在 ABCD中,O是BD的中点,EF过点O,下列结论:①AB∥DC;②EO=ED;③∠A=∠C;④S四边形ABOE=S四边形CDOF,其中正确结论的个数为 ( )
A.1
B.2
C.3
D.4
C
8.(2024·天津)如图,在△ABC中,∠B=30°,将△ABC绕点C顺时针旋转60°得到△DEC,点A,B的对应点分别为D,E,延长BA交DE于点F,下列结论中一定正确的是 ( )
A.∠ACB=∠ACD
B.AC∥DE
C.AB=EF
D.BF⊥CE
D
9.(2024·银川区模拟)如图,在正方形ABCD中,连接BD,BE平分∠ABD交AD于点E,F是AD边上一点,连接CF交BD于点G,CF=BE,连接AG交BE于点H.下列结论中错误的是 ( )
A.△ABE≌△DCF
B.AG=CG
C.BE⊥AG
D.DF=EF
D
D
A
解析:∠B′C′A=∠AC′C=∠C=72°,∴∠BC′B′=36°=∠AB′C′,∴AB′∥BC.
重难题型二 多结论选填题
类型一:代数多结论选填题
如图,抛物线y=ax2+bx+c(a≠0)与x轴
交于点A,B,与y轴交于点C,对称轴为直线
x=-1.若点A的坐标为(-4,0),则下列结论中
正确的是 ( )
A.2a+b=0
B.4a-2b+c>0
C.x=2是关于x的一元二次方程ax2+bx+c=0(a≠0)的一个根
D.点(x1,y1),(x2,y2)在抛物线上,当x1>x2>-1时,y1<y2<0
C
【分层分析】∵对称轴为直线x=-1,∴b= ,∴2a-b= ,故可判断A,∵点A的坐标为(-4,0),∴当x=-2时,y=4a-2b+c< ,故可判断B,易得抛物线与x轴的另一个交点为 ,故可判断C,当X 时,y随x的增大而增大,∴当x1>x2>-1时,y1 y2,故可判断D.
2a
0
0
(2,0)
>-1
>
1.(2024·滁州模拟)如图,已知直线y=3x+b与y=ax-2的交点的横坐标为-2,根据图象,下列结论中错误的是 ( )
A.a>0
B.b>0
C.x=-2是方程3x+b=ax-2的解
D.x>-2是不等式ax-2>3x+b的解集
D
2.已知抛物线y=ax2+bx+c(a≠0)的图象如图所示,则下列结论中正确的是 ( )
A.abc<0
B.a-b=0
C.3a-c=0
D.am2+bm≤a-b(m为任意实数)
D
C
类型二:几何多结论选填题
(2024T8)
4.(2024·河北)如图,AD与BC交于点O,△ABO和△CDO关于直线PQ对称,点A,B的对称点分别是点C,D.下列结论中不一定正确的是( )
A.AD⊥BC B.AC⊥PQ
C.△ABO ≌△CDO D.AC∥BD
A
5.(2024·湖南)如图,在△ABC中,D,E分别为边AB,AC的中点.下列结论中错误的是 ( )
A.DE∥BC
B.△ADE∽△ABC
C.BC=2DE
D.S△ADE=S△ABC
D
6.(2023·苏州)如图,在正方形网格内,线段PQ的两个端点都在格点上,网格内另有A,B,C,D四个格点,下面四个结论中,正确的是 ( )
A.连接AB,则AB∥PQ
B.连接BC,则BC∥PQ
C.连接BD,则BD⊥PQ
D.连接AD,则AD⊥PQ
B
7.(2024·眉山)如图,在 ABCD中,O是BD的中点,EF过点O,下列结论:①AB∥DC;②EO=ED;③∠A=∠C;④S四边形ABOE=S四边形CDOF,其中正确结论的个数为 ( )
A.1
B.2
C.3
D.4
C
8.(2024·天津)如图,在△ABC中,∠B=30°,将△ABC绕点C顺时针旋转60°得到△DEC,点A,B的对应点分别为D,E,延长BA交DE于点F,下列结论中一定正确的是 ( )
A.∠ACB=∠ACD
B.AC∥DE
C.AB=EF
D.BF⊥CE
D
9.(2024·银川区模拟)如图,在正方形ABCD中,连接BD,BE平分∠ABD交AD于点E,F是AD边上一点,连接CF交BD于点G,CF=BE,连接AG交BE于点H.下列结论中错误的是 ( )
A.△ABE≌△DCF
B.AG=CG
C.BE⊥AG
D.DF=EF
D
D
A
解析:∠B′C′A=∠AC′C=∠C=72°,∴∠BC′B′=36°=∠AB′C′,∴AB′∥BC.
同课章节目录
