中考数学复习专项突破重难题型三 课件(共23张PPT)
文档属性
| 名称 | 中考数学复习专项突破重难题型三 课件(共23张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 1.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-03-30 13:18:10 | ||
图片预览


文档简介
(共23张PPT)
重难题型三 与阴影面积有关的计算题
方法1:直接公式法
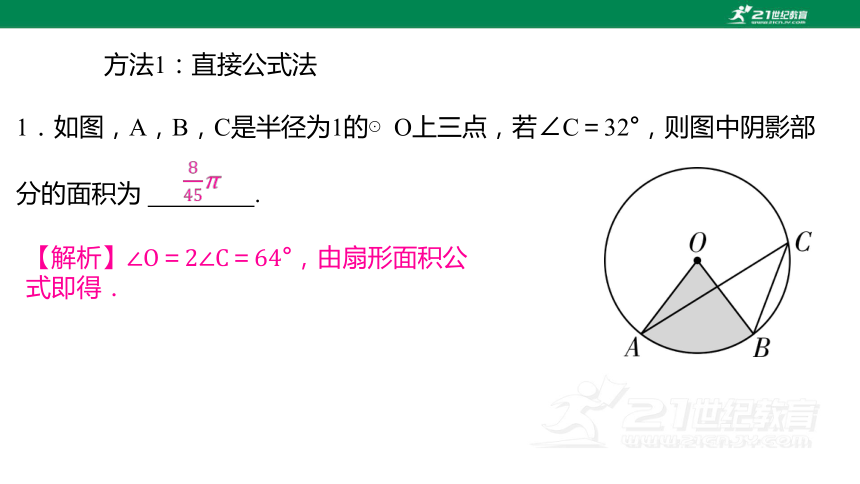
1.如图,A,B,C是半径为1的⊙O上三点,若∠C=32°,则图中阴影部分的面积为 .
【解析】∠O=2∠C=64°,由扇形面积公式即得.
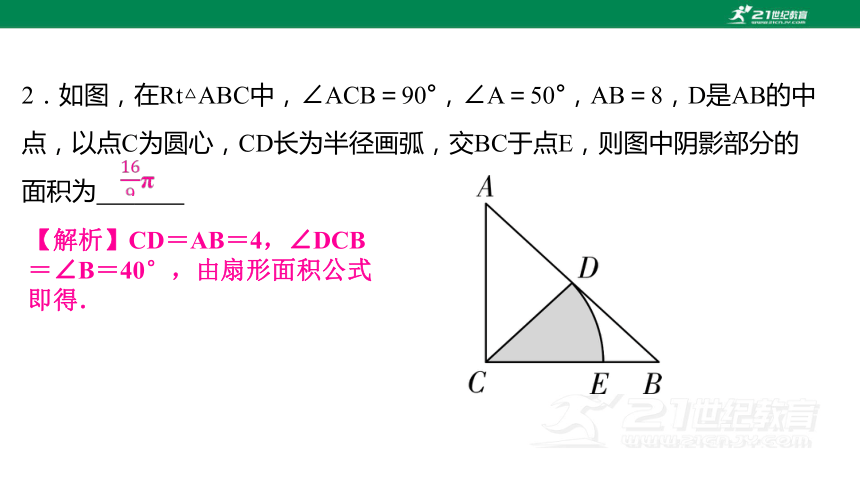
2.如图,在Rt△ABC中,∠ACB=90°,∠A=50°,AB=8,D是AB的中点,以点C为圆心,CD长为半径画弧,交BC于点E,则图中阴影部分的面积为 5
【解析】CD=AB=4,∠DCB=∠B=40°,由扇形面积公式即得.
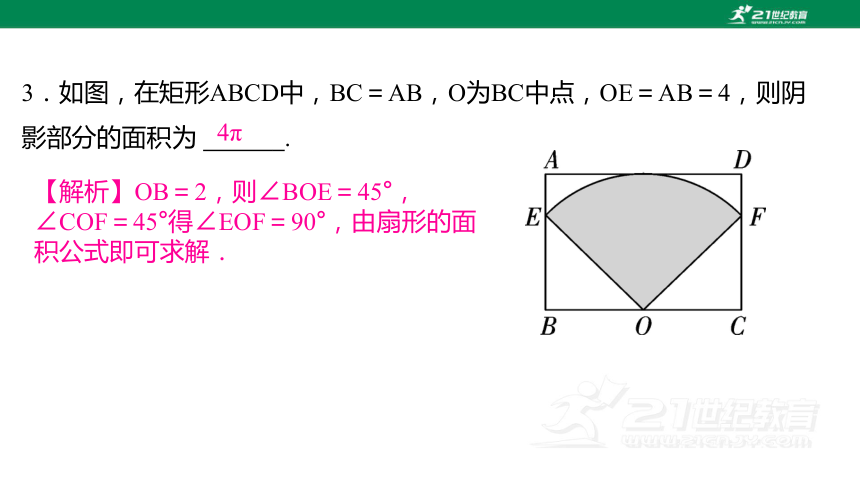
3.如图,在矩形ABCD中,BC=AB,O为BC中点,OE=AB=4,则阴影部分的面积为 5.
4π
【解析】OB=2,则∠BOE=45°,∠COF=45°得∠EOF=90°,由扇形的面积公式即可求解.
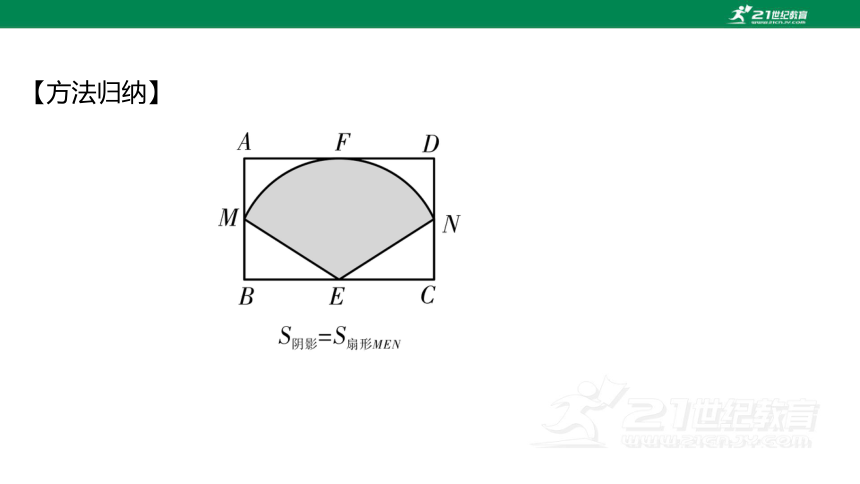
【方法归纳】
方法2:和差法
(一)直接和差法
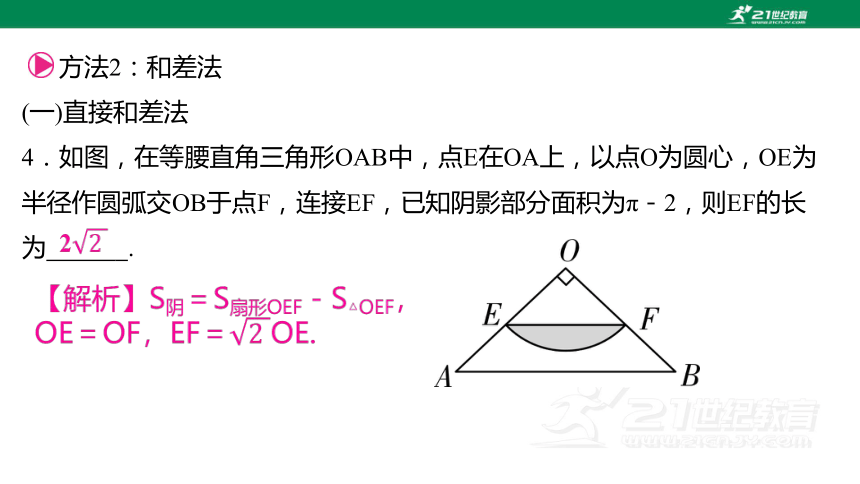
4.如图,在等腰直角三角形OAB中,点E在OA上,以点O为圆心,OE为半径作圆弧交OB于点F,连接EF,已知阴影部分面积为π-2,则EF的长为 5.
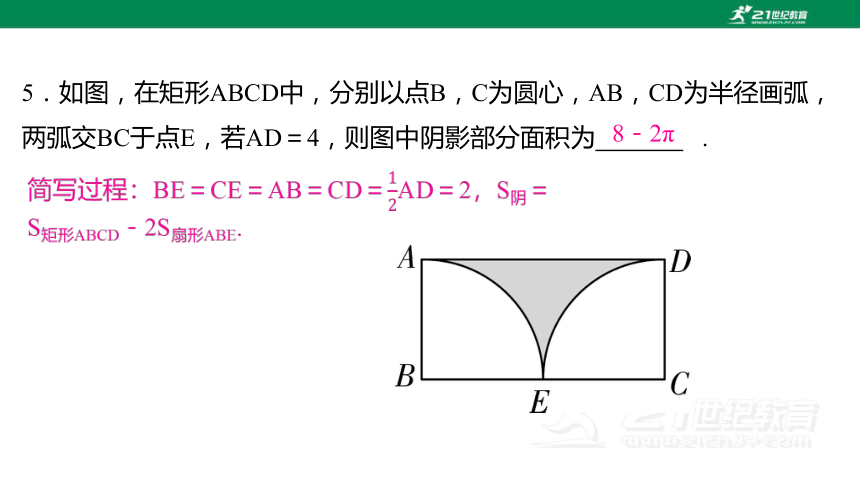
5.如图,在矩形ABCD中,分别以点B,C为圆心,AB,CD为半径画弧,两弧交BC于点E,若AD=4,则图中阴影部分面积为 5 .
8-2π
【方法归纳】
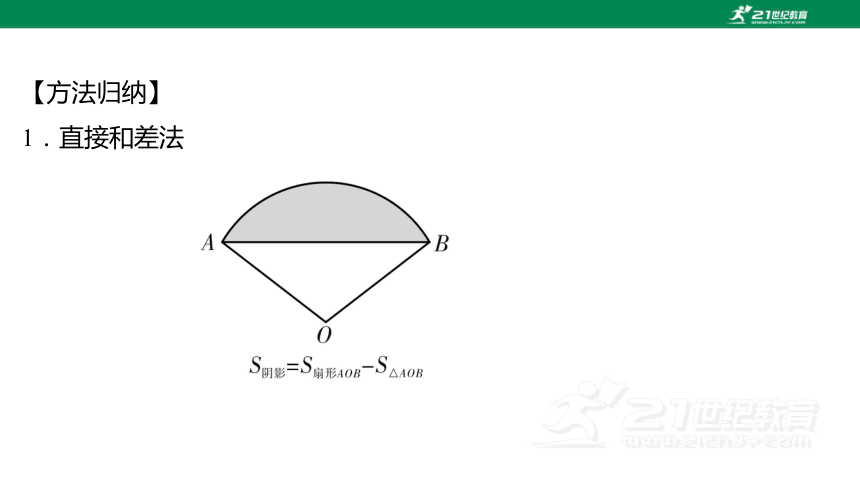
1.直接和差法
(二)构造和差法
6.如图,△ABC是⊙O的内接三角形,AD为⊙O的直径,若AC=2,∠ABC=60°,则图中阴影部分的面积为 5 .
【解析】连接OC,CD,S阴=S△OAC+S扇形ODC.
7.如图,P是⊙O直径AB延长线的一点,过点P作⊙O的切线,C为切点,D是的中点,连接AD,OC,若∠P=36°,⊙O的半径为2,则阴影部分的面积为 5 .
【解析】连接OD,OD⊥AB,S阴=S扇形ODC+S△AOD.
构造和差法
方法3:转化法
8.如图,在矩形ABCD中,AB=1,∠ACB=30°,E为BC延长线上一点,以点B为圆心,BE长为半径画弧,该弧恰好经过点D,则图中阴影部分的面积为. 5 。
【解析】连接BD,∠DBC=30°,BD=BE=2,S阴=S扇形DBE.
9.如图,半圆O的直径AB=4,C是圆弧上一点,连接AC,BC,且AC=BC,以点A为圆心,AB长为半径作弧,交AC的延长线于点D,连接OC,则图中阴影部分的面积为 5 .
2π-2
【解析】C为的中点,∠DAB=45°,S阴=S扇形DAB-S△CAO.
【方法归纳】
1.直接等面积转化(CD∥AB)
2.对称转化法(D为AB的中点)
方法4:容斥原理
10.如图,在等边三角形ABC中,AB=AC=BC=8,分别以AB,AC,BC为直径作半圆,则图中阴影部分的面积是 .
【方法归纳】
有的阴影部分面积是由两个基本图形相互重叠得到的,常用的方法是:
“两个基本图形的面积之和”-“被重叠图形的面积”=“组合图形的面积”.
C
【解析】连接OE.S阴影=S△BOE-S扇形DOE.
B
D
A
C
17.如图,在Rt△ABC中,∠C=90°,AC=BC=2,D是AB的中点,以点A,B为圆心,AD,BD长为半径画弧,分别交AC,BC于点E,F,则图中阴影部分的面积为 .
重难题型三 与阴影面积有关的计算题
方法1:直接公式法
1.如图,A,B,C是半径为1的⊙O上三点,若∠C=32°,则图中阴影部分的面积为 .
【解析】∠O=2∠C=64°,由扇形面积公式即得.
2.如图,在Rt△ABC中,∠ACB=90°,∠A=50°,AB=8,D是AB的中点,以点C为圆心,CD长为半径画弧,交BC于点E,则图中阴影部分的面积为 5
【解析】CD=AB=4,∠DCB=∠B=40°,由扇形面积公式即得.
3.如图,在矩形ABCD中,BC=AB,O为BC中点,OE=AB=4,则阴影部分的面积为 5.
4π
【解析】OB=2,则∠BOE=45°,∠COF=45°得∠EOF=90°,由扇形的面积公式即可求解.
【方法归纳】
方法2:和差法
(一)直接和差法
4.如图,在等腰直角三角形OAB中,点E在OA上,以点O为圆心,OE为半径作圆弧交OB于点F,连接EF,已知阴影部分面积为π-2,则EF的长为 5.
5.如图,在矩形ABCD中,分别以点B,C为圆心,AB,CD为半径画弧,两弧交BC于点E,若AD=4,则图中阴影部分面积为 5 .
8-2π
【方法归纳】
1.直接和差法
(二)构造和差法
6.如图,△ABC是⊙O的内接三角形,AD为⊙O的直径,若AC=2,∠ABC=60°,则图中阴影部分的面积为 5 .
【解析】连接OC,CD,S阴=S△OAC+S扇形ODC.
7.如图,P是⊙O直径AB延长线的一点,过点P作⊙O的切线,C为切点,D是的中点,连接AD,OC,若∠P=36°,⊙O的半径为2,则阴影部分的面积为 5 .
【解析】连接OD,OD⊥AB,S阴=S扇形ODC+S△AOD.
构造和差法
方法3:转化法
8.如图,在矩形ABCD中,AB=1,∠ACB=30°,E为BC延长线上一点,以点B为圆心,BE长为半径画弧,该弧恰好经过点D,则图中阴影部分的面积为. 5 。
【解析】连接BD,∠DBC=30°,BD=BE=2,S阴=S扇形DBE.
9.如图,半圆O的直径AB=4,C是圆弧上一点,连接AC,BC,且AC=BC,以点A为圆心,AB长为半径作弧,交AC的延长线于点D,连接OC,则图中阴影部分的面积为 5 .
2π-2
【解析】C为的中点,∠DAB=45°,S阴=S扇形DAB-S△CAO.
【方法归纳】
1.直接等面积转化(CD∥AB)
2.对称转化法(D为AB的中点)
方法4:容斥原理
10.如图,在等边三角形ABC中,AB=AC=BC=8,分别以AB,AC,BC为直径作半圆,则图中阴影部分的面积是 .
【方法归纳】
有的阴影部分面积是由两个基本图形相互重叠得到的,常用的方法是:
“两个基本图形的面积之和”-“被重叠图形的面积”=“组合图形的面积”.
C
【解析】连接OE.S阴影=S△BOE-S扇形DOE.
B
D
A
C
17.如图,在Rt△ABC中,∠C=90°,AC=BC=2,D是AB的中点,以点A,B为圆心,AD,BD长为半径画弧,分别交AC,BC于点E,F,则图中阴影部分的面积为 .
同课章节目录
