中考数学复习专项突破重难题型七 课件(共46张PPT)
文档属性
| 名称 | 中考数学复习专项突破重难题型七 课件(共46张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 4.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-03-30 00:00:00 | ||
图片预览










文档简介
(共46张PPT)
类型一:单动点探究之几何最值问题
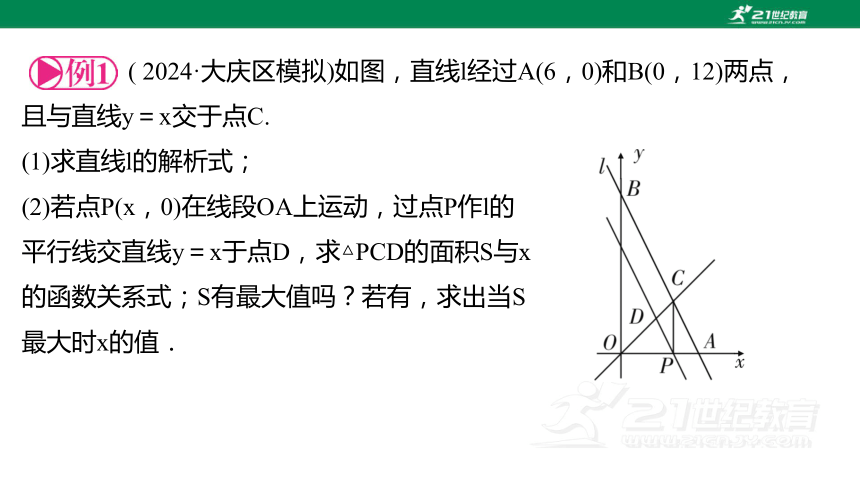
( 2024·大庆区模拟)如图,直线l经过A(6,0)和B(0,12)两点,且与直线y=x交于点C.
(1)求直线l的解析式;
(2)若点P(x,0)在线段OA上运动,过点P作l的
平行线交直线y=x于点D,求△PCD的面积S与x
的函数关系式;S有最大值吗?若有,求出当S
最大时x的值.
1.(2019·宁夏第26题10分)如图,在△ABC中,∠A=90°,AB=3,AC=4,点M, Q分别是边AB,BC上的动点(点M不与A, B重合), 且MQ⊥BC,过点M作BC的平行线MN,交AC于点N,连接NQ,设BQ为x.
(1)试说明不论x为何值时,总有△QBM∽△ABC;
(2)是否存在一点Q,使得四边形BMNQ为平行
四边形,试说明理由;
(3)当x为何值时,四边形BMNQ的面积最大,
并求出最大值.
解:(1)∵MQ⊥BC,
∴∠MQB=90°,
∴∠MQB=∠CAB,
又∠QBM=∠ABC,∴△QBM∽△ABC.
∴不论x为何值时,总有△QBM∽△ABC.
(2)当BQ=MN时,四边形BMNQ为平行四边形,∵MN∥BQ且BQ=MN,
∴四边形BMNQ为平行四边形.
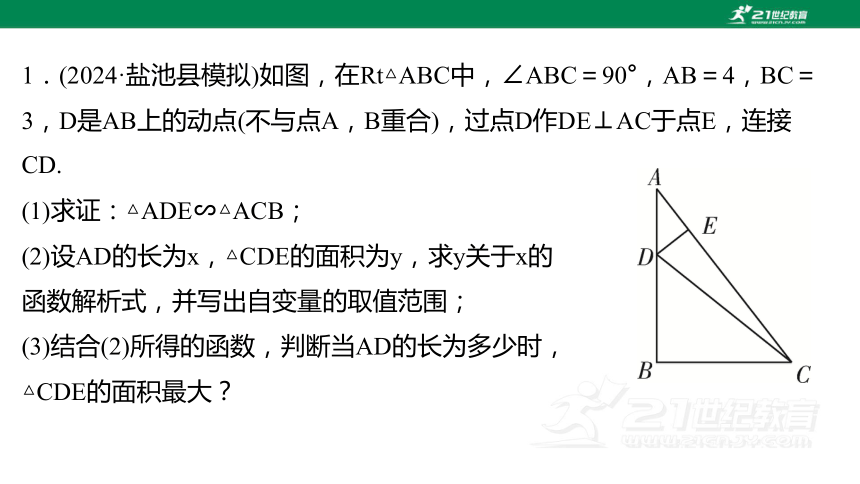
1.(2024·盐池县模拟)如图,在Rt△ABC中,∠ABC=90°,AB=4,BC=3,D是AB上的动点(不与点A,B重合),过点D作DE⊥AC于点E,连接
CD.
(1)求证:△ADE∽△ACB;
(2)设AD的长为x,△CDE的面积为y,求y关于x的
函数解析式,并写出自变量的取值范围;
(3)结合(2)所得的函数,判断当AD的长为多少时,
△CDE的面积最大?
(1)证明:∵DE⊥AC,
∴∠AED=90°=∠ABC,
∵∠DAE=∠CAB,
∴△ADE∽△ACB.
类型二:双动点探究之几何最值问题
(2024·银川模拟)如图,△ABC是边长为4 cm 的等边三角形,AD为△ABC的中线.动点P,Q分别从A,B两点同时出发,分别沿AB,BC方向做匀速运动,它们的速度都是 1 cm/s.当点P到达点B时,P,Q两点停止运动,设点P的运动时间为t(s).解答下列问题:
(1)当t= 时,△PBQ为等边三角形;
(2)设四边形APQC的面积S,试求出S与t之间的
函数关系式;并求出当t为何值时,四边形APQC的
面积最小?并且求出最小值.
2
【分层分析】(1)由BP= 求得结果;(2)分别计算出△ABC和△BPQ的面积,进而求得S的函数关系式,求出这个二次函数的最小值即可.
BQ
2.(2021·宁夏第26题10分节选)如图,已知直线y=kx+3与x轴的正半轴交于点A,与y轴交于点B,sin∠OAB=.
(1)求k的值;
(2)D,E两点同时从坐标原点O出发,其中点D以
每秒1个单位长度的速度,沿O→A→B的路线运动,
点E以每秒2个单位长度的速度,沿O→B→A的路线运动.当D,E两点相遇时,它们都停止运动,设运动时间为t s.若设△OED的面积为S,求S关于t的函数关系式,并求出t为多少时,S的值最大.
类型三:平移探究之几何最值问题
(2024·石嘴山模拟)如图,在△ABC中,AB=AC=1,∠A=45°,边长为1的正方形的一个顶点D在边AC上,与△ABC另两边分别交于点E,F,DE∥AB,将正方形平移,使点D保持在AC上(D不与A重合),设AF=x,正方形与△ABC重叠部分的面积为y.
(1)求y与x的函数关系式并写出自变量x的取值范围;
(2)x为何值时,y的值最大?
【分层分析】(1)当点D保持在AC上时,正方形与△ABC重叠部分为直角梯形 ,根据直角梯形的面积公式,只需用含x的代数式分别表示出上底 、下底 及高 的长度即可.由△ADF为等腰直角三角形,可得高DF= ;则AD= ,下底BF= ,进而得出CD,再根据等腰三角形及平行线的性质可证∠C= ,得出上底DE根据点D保持在 上,且D不与A重合,可知 <AD≤ ,从而求出自变量x的取值范围;(2)由(1)知,y是x的二次函数,根据二次函数的性质,即可得到结论.
DEBF
DE
BF
DF
x
1-x
∠CED
AC
0
1
5.(2024·灵武模拟)在△EFG中,∠G=90°,EG=FG=2,正方形ABCD的边长为1,将正方形ABCD和△EFG如图放置,AD与EF在一条直线上,点A与点E重合.现将正方形ABCD沿EF方向以每秒1个单位长度的速度匀速移动,当点A与点F重合时停止.在这个运动过程中,正方形ABCD和
△EFG重叠部分的面积为S,运动时间为t s.
(1)求出S关于t的函数解析式,并写出t的取值范围;
(2)当t为多少时,S有最大值?最大值是多少?
答图①
答图②
6.(2024·西吉县模拟)如图,在平面直角坐标系中,四边形OABC为菱形,点C的坐标为(8,0),∠AOC=60°,垂直于x轴的直线l从y轴出发,沿x轴正方向以每秒1个单位长度的速度运动,设直线l与菱形OABC的两边分别交于点M,N(点M在点N的上方).
(1)求A,B两点的坐标;
(2)设△OMN的面积为S,直线l的运动时间为
t s(0≤t≤12),求S与t的函数关系式;
(3)在(2)的条件下,t为何值时,S最大?求出S的最大值.
类型一:单动点探究之几何最值问题
( 2024·大庆区模拟)如图,直线l经过A(6,0)和B(0,12)两点,且与直线y=x交于点C.
(1)求直线l的解析式;
(2)若点P(x,0)在线段OA上运动,过点P作l的
平行线交直线y=x于点D,求△PCD的面积S与x
的函数关系式;S有最大值吗?若有,求出当S
最大时x的值.
1.(2019·宁夏第26题10分)如图,在△ABC中,∠A=90°,AB=3,AC=4,点M, Q分别是边AB,BC上的动点(点M不与A, B重合), 且MQ⊥BC,过点M作BC的平行线MN,交AC于点N,连接NQ,设BQ为x.
(1)试说明不论x为何值时,总有△QBM∽△ABC;
(2)是否存在一点Q,使得四边形BMNQ为平行
四边形,试说明理由;
(3)当x为何值时,四边形BMNQ的面积最大,
并求出最大值.
解:(1)∵MQ⊥BC,
∴∠MQB=90°,
∴∠MQB=∠CAB,
又∠QBM=∠ABC,∴△QBM∽△ABC.
∴不论x为何值时,总有△QBM∽△ABC.
(2)当BQ=MN时,四边形BMNQ为平行四边形,∵MN∥BQ且BQ=MN,
∴四边形BMNQ为平行四边形.
1.(2024·盐池县模拟)如图,在Rt△ABC中,∠ABC=90°,AB=4,BC=3,D是AB上的动点(不与点A,B重合),过点D作DE⊥AC于点E,连接
CD.
(1)求证:△ADE∽△ACB;
(2)设AD的长为x,△CDE的面积为y,求y关于x的
函数解析式,并写出自变量的取值范围;
(3)结合(2)所得的函数,判断当AD的长为多少时,
△CDE的面积最大?
(1)证明:∵DE⊥AC,
∴∠AED=90°=∠ABC,
∵∠DAE=∠CAB,
∴△ADE∽△ACB.
类型二:双动点探究之几何最值问题
(2024·银川模拟)如图,△ABC是边长为4 cm 的等边三角形,AD为△ABC的中线.动点P,Q分别从A,B两点同时出发,分别沿AB,BC方向做匀速运动,它们的速度都是 1 cm/s.当点P到达点B时,P,Q两点停止运动,设点P的运动时间为t(s).解答下列问题:
(1)当t= 时,△PBQ为等边三角形;
(2)设四边形APQC的面积S,试求出S与t之间的
函数关系式;并求出当t为何值时,四边形APQC的
面积最小?并且求出最小值.
2
【分层分析】(1)由BP= 求得结果;(2)分别计算出△ABC和△BPQ的面积,进而求得S的函数关系式,求出这个二次函数的最小值即可.
BQ
2.(2021·宁夏第26题10分节选)如图,已知直线y=kx+3与x轴的正半轴交于点A,与y轴交于点B,sin∠OAB=.
(1)求k的值;
(2)D,E两点同时从坐标原点O出发,其中点D以
每秒1个单位长度的速度,沿O→A→B的路线运动,
点E以每秒2个单位长度的速度,沿O→B→A的路线运动.当D,E两点相遇时,它们都停止运动,设运动时间为t s.若设△OED的面积为S,求S关于t的函数关系式,并求出t为多少时,S的值最大.
类型三:平移探究之几何最值问题
(2024·石嘴山模拟)如图,在△ABC中,AB=AC=1,∠A=45°,边长为1的正方形的一个顶点D在边AC上,与△ABC另两边分别交于点E,F,DE∥AB,将正方形平移,使点D保持在AC上(D不与A重合),设AF=x,正方形与△ABC重叠部分的面积为y.
(1)求y与x的函数关系式并写出自变量x的取值范围;
(2)x为何值时,y的值最大?
【分层分析】(1)当点D保持在AC上时,正方形与△ABC重叠部分为直角梯形 ,根据直角梯形的面积公式,只需用含x的代数式分别表示出上底 、下底 及高 的长度即可.由△ADF为等腰直角三角形,可得高DF= ;则AD= ,下底BF= ,进而得出CD,再根据等腰三角形及平行线的性质可证∠C= ,得出上底DE根据点D保持在 上,且D不与A重合,可知 <AD≤ ,从而求出自变量x的取值范围;(2)由(1)知,y是x的二次函数,根据二次函数的性质,即可得到结论.
DEBF
DE
BF
DF
x
1-x
∠CED
AC
0
1
5.(2024·灵武模拟)在△EFG中,∠G=90°,EG=FG=2,正方形ABCD的边长为1,将正方形ABCD和△EFG如图放置,AD与EF在一条直线上,点A与点E重合.现将正方形ABCD沿EF方向以每秒1个单位长度的速度匀速移动,当点A与点F重合时停止.在这个运动过程中,正方形ABCD和
△EFG重叠部分的面积为S,运动时间为t s.
(1)求出S关于t的函数解析式,并写出t的取值范围;
(2)当t为多少时,S有最大值?最大值是多少?
答图①
答图②
6.(2024·西吉县模拟)如图,在平面直角坐标系中,四边形OABC为菱形,点C的坐标为(8,0),∠AOC=60°,垂直于x轴的直线l从y轴出发,沿x轴正方向以每秒1个单位长度的速度运动,设直线l与菱形OABC的两边分别交于点M,N(点M在点N的上方).
(1)求A,B两点的坐标;
(2)设△OMN的面积为S,直线l的运动时间为
t s(0≤t≤12),求S与t的函数关系式;
(3)在(2)的条件下,t为何值时,S最大?求出S的最大值.
同课章节目录
