中考数学复习专项突破重难题型九 课件(共103张PPT)
文档属性
| 名称 | 中考数学复习专项突破重难题型九 课件(共103张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 7.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-03-30 13:21:40 | ||
图片预览










文档简介
(共103张PPT)
类型一:几何模型迁移综合实践型
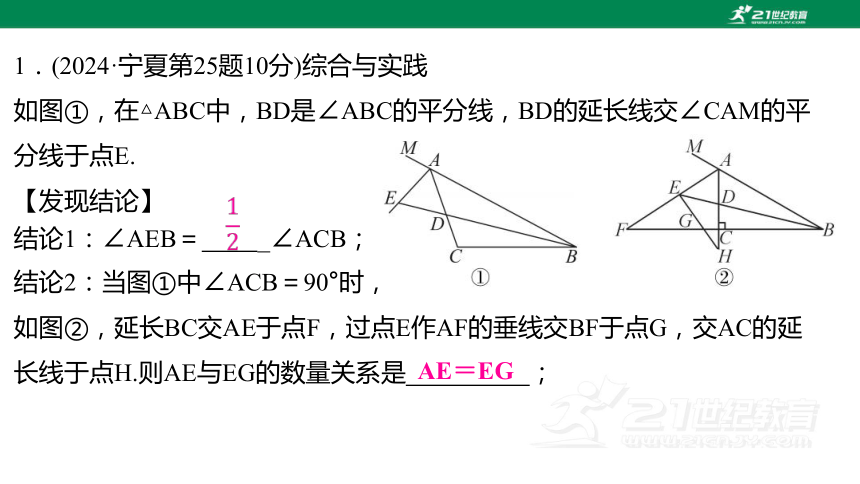
1.(2024·宁夏第25题10分)综合与实践
如图①,在△ABC中,BD是∠ABC的平分线,BD的延长线交∠CAM的平分线于点E.
【发现结论】
结论1:∠AEB= _∠ACB;
结论2:当图①中∠ACB=90°时,
如图②,延长BC交AE于点F,过点E作AF的垂线交BF于点G,交AC的延长线于点H.则AE与EG的数量关系是 ;
AE=EG
【应用结论】
(1)求证:AH=GF;
证明:(1)在Rt△AFC中,∠EFG+∠EAH=90°,
在Rt△AEH中,∠AHE+∠EAH=90°,
∴∠EFG=∠EHA,
又∵∠FEG=∠AEH,EG=EA,
∴△EFG≌△EHA(AAS),∴AH=GF.
第1课时 “a=b”型的线段问题
“
a=b”型
(1)若a与b分别在不同的三角形中,
则直接证明对应所在三角形全等.
(2)若a与b不共线但共顶点,则证明所在三角形是等腰三角形.
(3)若a与b共线且共顶点,常用证明方法是作平行线,先构造一组三
角形全等得到一组对应边相等,再证明“8”字三角形全等(如图①).
需要证明:BD=DC.过点C作CF∥AB交ED的延长线于点F.
先构造一组三角形全等,得到对应边相等,即BE=CF或ED=DF,
再构造“8”字三角形△BED≌△CFD,得到BD=DC.
(4)若a与b垂直,常用证明方法是构造直角三角形,证明最大的三角形是等腰直角三角形,利用斜边的中点可得结论(如图②).
需要证明:BA=BC.
延长AB到点D,使得AB=BD,连接AC,DC.
先利用旋转型或双垂直型模型证明△ACD是直角三角形,
再利用斜边上的中点得到BA=BC.
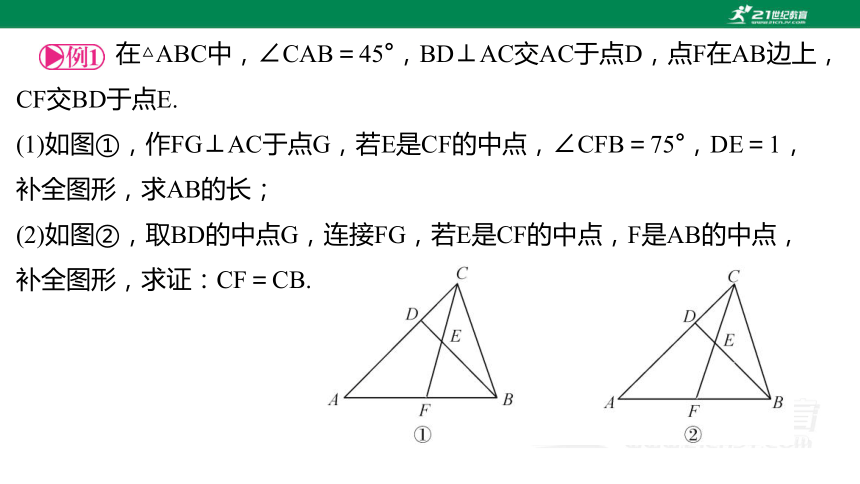
在△ABC中,∠CAB=45°,BD⊥AC交AC于点D,点F在AB边上,CF交BD于点E.
(1)如图①,作FG⊥AC于点G,若E是CF的中点,∠CFB=75°,DE=1,补全图形,求AB的长;
(2)如图②,取BD的中点G,连接FG,若E是CF的中点,F是AB的中点,补全图形,求证:CF=CB.
【方法总结】证明两条线段相等,除了构造三角形全等,还可以证明它是等腰三角形或者利用等腰三角形三线合一的方法来证明.
1.如图,在△ABC中,AB=AC,∠BAC=90°.
【发现结论】
(1)当BD平分∠ABC交AC于点D,F为BC上一点,连接AF交BD于点E.
结论1:若AB=BF,则∠BEF= 5 ;
结论2:如图①,若AF⊥BD,过点C作CM⊥AF交AF的延长线于点M,则AD与CF的数量关系是 5 ;
90°
AD=CF
①
【应用结论】
(2)如图②,BD平分∠ABC交AC于点D,CE⊥BD,垂足E在BD的延长线上.延长BA,CE相交于点F,试判断线段CE和BD的数量关系,并说明理由;
解:(2)BD=2CE.
理由:∵BD平分∠ABC,∴∠ABD=∠CBD,
∴△BCE≌△BFE(ASA),∴CE=EF,
∵∠BAC=90°,CE⊥BD,
∴∠ACF+∠F=90°,∠ABD+∠F=90°,
∴∠ABD=∠ACF,∴△ABD≌△ACF(ASA),
∴BD=CF,∵CF=CE+EF=2CE,∴BD=2CE.
②
2.【模型启迪】
(1)如图①,在△ABC中,D为BC边的中点,连接AD并延长至点H.使DH=AD,连接CH.由∠ADB=∠CDH,得△ADB≌△HDC,则AB与CH的数量关系为 ,位置关系为 ;
AB=CH
AB∥CH
【模型探索】
(2)如图②,在△ABC中,AP平分∠BAC,D为BC边的中点,过点D作DQ∥AP,交CA的延长线于点Q,交AB边于点K,作BH∥CQ,交QD的延长线于点H,试判断BK与CQ的数量关系,并说明理由;
(2)解:BK=CQ,理由:由题意得∠H=∠Q,
∵DQ∥AP,∴∠Q=∠CAP,∠BKH=∠BAP,
∴∠H=∠CAP,∵AP平分∠BAC,∴∠CAP=∠BAP,
∴∠H=∠BKH,∴BK=BH,∵D为BC边的中点,
∴BD=CD,∵∠BDH=∠CDQ,∴△BDH≌△CDQ(AAS),
∴BH=CQ,∴BK=CQ.
(3)如图③,在△ABC中,D为BC的中点,连接AD,E为AC边上一点,过点E作EG⊥AD于点G,连接BE交AD于点F,且BF=AC.作BR∥AC,交AD的延长线于点R,补全图形,求证:AG=GF.
(3)证明:由题意得∠R=∠CAD,
∵D为BC的中点,∴BD=CD,
∵∠RDB=∠ADC,∴△RDB≌△ADC(AAS),
∴RB=AC,∵BF=AC,∴RB=BF,∴∠R=∠BFR,
∴∠BFR=∠CAD,∴∠AFE=∠BFR=∠CAD,
∴AE=FE,∵EG⊥AD,∴AG=GF.
第2课时 “a=b+c”型的线段和差问题
针对几何题目中涉及三条线段之间的和、差关系(a=b+c),我们一般采用截长补短或类似截长补短的方法.
1.截长补短法
有一类几何题,其命题主要是证明三条线段长度的“和”或“差”或比例关系,一般可以采取截长或补短的方法进行求解,所谓“截长”,就是将三者中最长的那条线段一分为二,使其中的一条线段与已知线段相等,然后证明其中的另一条线段与已知的另一条线段的大小关系,所谓“补短”,就是将一条已知的较短的线段延长,延长部分与另一条已知的较短的线段的长度相等,然后求出延长后的线段与最长的已知线段的大小关系.有的是采取截长补短的方法后,使之构成某种特定的三角形进行求解.
(1)截长法:①过某一点作长边的垂线;②在长边截取一条与某一短边相等的线段,再证剩下的线段与另一短边相等.
(2)补短法:①延长短边;②通过旋转等方式使两短边拼合在一起.
2.类似截长补短
这类几何题主要是借助题目给出的条件,如角平分线,等腰三角形等作出类似于截长补短的辅助线求解.
(2024·银川区模拟)已知△ABC是等边三角形.
(1)如图①,若AB=4,点D在线段BC上,且BD=1,连接AD,过点D作DE⊥AB于点E,请补全图形,求AD的长;
(2)如图②,E是BC延长线上一点,∠AEF=60°,EF交△ABC的外角平分线于点F,在线段CF上截取一点G,使得CG=CE,连接EG,请补全图形,求证:CF=AC+CE.
(2)证明:∵△ABC是等边三角形,∴∠ACB=60°,
∴∠ACE=180°-∠ACB=120°,
∵CF平分∠ACE,∴∠ACF=∠ECF=60°,
∴△CEG是等边三角形,∴CE=GE,
∠CEG=∠CGE=60°=∠AEF,
∴∠FGE=∠ACE=120°,∠CEA=∠GEF,
∴△ACE≌△FGE(ASA),∴AC=FG,∴CF=CG+GF=AC+CE.
【方法归纳】根据问题的特征“a=b+c”,可以快速判断是否采用截长补短法,关键是在进行截长或补短后,是否可以证明三角形全等,或者是否为等腰三角形,是判断方法是否准确的重要评判手段.
3.【问题背景】如图①,已知AM∥BN,AE平分∠BAM,BE平分∠ABN,过点E的直线交射线AM于点C,交射线BN于点D.探究图中AC,BD,AB之间的数量关系.
(1)小王同学探究此问题的方法是:延长AE交BN于点F,先证∠AEB=90°,说明△ABE≌△FBE,再证△ACE≌△FDE,可得出结论: ;
AB=BD+AC
【探索延伸】如图②,已知AM∥BN,AE平分∠BAM,BE平分∠ABN,过点E的直线交射线AM的反向延长线于点C,交射线BN于点D.延长AE交BD于点G.
(2)试判断AC,BD与AB之间的数量关系,并说明理由;
(3)若AB=5,AC=3,S△ABE-S△ACE=4,
求S△BDE.
4.【模型建立】
如图,在正方形ABCD中,E,F分别是BC,CD边上的点
(点E不与点B,C重合),且∠EAF=45°.
(1)当BE=DF时,求证:AE=AF;
【模型应用】
(2)在CD的延长线上截取DM=BE,
猜想BE,EF,DF三条线段之间存在的数量关系,并证明;
【模型迁移】
(3)连接AC,G是CB延长线上一点,GH⊥AE,垂足为K,交AC于点H且GH=AE.作HR⊥BC于点R,若DF=a,CH=b,补全图形,请用含a,b的代数式表示EF的长
(1)证明:由题意得AB=AD,∠B=∠D=90°,BE=DF,
∴△ABE≌△ADF(SAS),∴AE=AF.
(2)解:BE+DF=EF,
证明:易证△ABE≌△ADM(SAS),∴∠BAE=∠DAM,AM=AE,
∵四边形ABCD是正方形,∴∠BAD=90°,∵∠EAF=45°,
∴∠BAE+∠DAF=45°,∴∠DAM+∠DAF=45°,即∠MAF=45°,
∴∠MAF=∠EAF,∴△MAF≌△EAF(SAS),∴FM=FE,
∴DM+DF=EF,∴BE+DF=EF.
证明与 有关的线段数量关系时,常通过构造等腰直角三角形解决问题.
(2)如图②,延长BD至点G,使AG=AC,作∠BAG的平分线交BD于点H,交GC的延长线于点K.过点A作AQ⊥AK交KB的延长线于点Q,请补全图形,求证:CK+GK=AK.
证明:(1)∵AC是正方形ABCD的对角线,
∴AB=AD,∠BAE=∠DAE=45°,
∴△ABE≌△ADE(SAS),∴BE=DE.
(2)∵四边形ABCD是正方形,∴∠GAD=90°,∴∠AGD+∠ADG=90°,
由(1)知△ABE≌△ADE,∴∠ADG=∠EBG,∴∠AGD+∠EBG=90°,
∵FB⊥BE,∴∠FBG+∠EBG=90°,∴∠AGD=∠FBG=∠FGB,
∴FG=FB.
6.【模型建立】
(1)如图①,△ABC和△BDE都是等边三角形,点C关于AD的对称点F在BD边上.
Ⅰ)求证:AE=CD;
Ⅱ)用等式写出线段AD,BD,DF的数量关系,
并说明理由;
(1)Ⅰ)证明:∵△ABC和△BDE都是等边三角形,
∴AB=BC,BE=BD,∠ABC=∠EBD=60°,
∴∠ABC-∠CBE=∠EBD-∠CBE,
∴∠ABE=∠CBD,∴△ABE≌△CBD(SAS),
∴AE=CD.
Ⅱ)解:AD=DF+BD.理由:∵△BDE是等边三角形,∴BD=DE.
∵点C与点F关于AD对称,∴CD=DF.由(1)知AE=CD,∴AE=DF.
∴AD=AE+DE=DF+BD.
【模型应用】
(2)如图②,△ABC是直角三角形,AB=AC,CD⊥BD,垂足为D,点C关于AD的对称点F在BD边上.过点B作BE⊥AD于点E,请补全图形,用等式写出线段AD,BD,DF的数量关系,并说明理由.
如图,在△ABC中,AB=AC,D是BC边上一点(点D不与端点重合).点D关于直线AB的对称点为点E,连接AD,DE.在直线AD上取一点F,使∠EFD=∠BAC,直线EF与直线AC交于点G.
(1)若∠BAC=60°,BD<CD,∠BAD=α,求∠AGE的度数(用含α的代数式表示);
(2)若∠BAC=60°,BD<CD,在CG上截取
CM=BD,连接BM,BE,AE,BM交AD于点H,
补全图形,用等式表示线段CG与DE之间的数量
关系,并证明.
解:(1)由题可得∠EFD=∠BAC=60°,
∵∠EFD=∠1+∠BAD=∠1+α,
∴∠1=60°-α,∵∠AGE+∠1+∠BAC=180°,
∴∠AGE=180°-60°-∠1=120°-∠1,
∴∠AGE=120°-(60°-α)=60°+α.
【方法归纳】在等边三角形中有垂直或有中点(中线),观察图形的形状,猜倍的关系,去证明是含30°的直角三角形.
类型二:数学文化迁移综合实践型
(2023T26,2022T26)
2.(2023·宁夏第26题10分)综合与实践
【问题背景】
数学小组发现国旗上五角星的五个角都是
顶角为36°的等腰三角形,对此三角形产生
了极大兴趣并展开探究.
【探究发现】
如图①,在△ABC中,∠A=36°,AB=AC.
(1)操作发现:将△ABC折叠,使边BC落在边BA上,点C的对应点是点E,折痕交AC于点D,连接DE,DB,则∠BDE= ,设AC=1,BC=x,那么AE= (用含x的式子表示);
72°
1-x
【拓展应用】
当等腰三角形的底与腰的比等于黄金比时,这个三角形叫黄金三角形.例如,图①中的△ABC是黄金三角形.
(3)如图②,在菱形ABCD中,∠BAD=72°,AB=1.求这个菱形较长对角线的长.
【拓展应用】
(3)如图③,在△ABC中, D为AB边上的一点(不与A, B重合),过点D作DE∥BC,交AC于点E,BE,CD相交于点F,连接AF并延长,与DE,BC分别交于M,N.请问直线AN是△ABC的黄金分割线吗?并说明理由.
10.(2024·同心县模拟)
(1)阅读理解
我国是最早了解勾股定理的国家之一,它被记载于我国古代的数学著作《周髀算经》中.汉代数学家赵爽为了证明勾股定理,创制了一幅如图①所示的“弦图”,后人称之为“赵爽弦图”.根据“赵爽弦图”写出勾股定理: 5 ;
a2+b2=c2
(2)问题解决
勾股定理的证明方法有很多,如图②是古代的一种证明方法:过正方形
ACDE的中心O,作FG⊥HP,将它分成4份,所分成的四部分和以BC为边的正方形恰好能拼成以AB为边的正方形.
若AC=12,BC=5,求EF的值;
(3)拓展探究
如图③,以正方形一边为斜边向外作直角三角形,再以该直角三角形的两直角边分别向外作正方形,重复这一过程就可以得到“勾股树”的部分图形.设大正方形N的边长为定值n,小正方形
A,B,C,D的边长分别为a,b,c,d.已知
∠1=∠2=∠3=α,当角α(0°<α<90°)变化
时,探究b与c的关系式,并写出该关系式及
解答过程(b与c的关系式用含n的式子表示).
类型三:与函数有关的综合实践型
(2020T25,2019T25)
3.(2020·宁夏第25题10分)在综合与实践活动中,活动小组的同学看到网上购鞋的鞋号(为正整数)与脚长(mm)的对应关系如表1:
鞋号
(正整数) 22 23 24 25 26 27 …
脚长
(mm) 160±2 165±2 170±2 175±2 180±2 185±2 …
为了方便对问题的研究,活动小组将表1中的数据进行了编号,并对脚长的数据bn定义为[bn].如表2:
序号n 1 2 3 4 5 6 …
鞋号an 22 23 24 25 26 27 …
脚长bn 160±2 165±2 170±2 175±2 180±2 185±2 …
脚长
[bn] 160 165 170 175 180 185 …
定义:对于任意正整数m,n,其中m>2.若[bn]=m,则m-2≤bn≤m+2.
如:[b4]=175表示175-2≤b4≤175+2,即173≤b4≤177.
(1)通过观察表2,猜想出an与序号n之间的关系式,[bn]与序号n之间的关系式;
(2)用含an的代数式表示[bn];计算鞋号为42的鞋适合的脚长范围;
(3)若脚长为271 mm,那么应购鞋的鞋号为多大?
解:(1)an=21+n;
[bn]=160+5(n-1)=5n+155.
(2)由an=21+n与[bn]=5n+155得
[bn]=5an+50,把an=42代入an=21+n得
n=21,∴[b21]=5×42+50=260,
则260-2≤b21≤260+2,即258≤b21≤262.
答:鞋号为42的鞋适合的脚长范围是258 mm~262 mm
(3)根据[bn]=5n+155可知[bn]能被5整除,
∵270-2≤271≤270+2,∴[bn]=270,
将[bn]=270代入[bn]=5an+50中得an=44.
故应购买44号的鞋.
4.(2019·宁夏第25题10分)在综合与实践活动中,活动小组对学校400 m的跑道进行规划设计.如图,跑道由两段直道和两端是半圆弧的跑道组成,其中400 m跑道最内圈为400 m,两端半圆弧的半径为36 m.(π取3.14)
(1)求400 m跑道中一段直道的长度;
(2)在活动中发现跑道周长(单位:m)随跑道宽度(距最内圈的距离,单位:m)的变化而变化.请完成下表:
跑道
宽度(m) 0 1 2 3 4 5 …
跑道
周长(m) 400 5 5 5 5 5 …
406.28
412.56
418.84
425.12
431.4
若设x表示跑道宽度(单位:m),y表示该跑道周长(单位:m),试写出y与x的函数解析式;
(3)将446 m的跑道周长作为400 m跑道场地的最外沿,那么它与最内圈(跑道周长400 m)形成的区域最多能铺设道宽为1.2 m 的跑道多少条?
解:(1)400 m跑道中一段直道的长度为
(400-2×36×3.14)÷2
=86.96(m).
(2)补充表格如表所示.
y与x的函数解析式为y=6.28x+400.
(3)当y=446时,即6.28x+400=446,
解得 x≈7.32,7.32÷1.2≈6 (条).
答:最多能铺设道宽为1.2 m的跑道6条.
11.通过学习我们知道,在水平面上推或拉一个物体时,在物体和水平面之间会产生阻碍物体运动的力,像这样的力是摩擦力.小明利用如图所示的装置测量在不同重量下某木块与木板之间的摩擦力.在木块上放置砝码,缓慢向左拉动水平放置的木板,当木块和砝码相对桌面静止且木板仍在继续滑动时,弹簧秤的示数即为木块受到的摩擦力的大小.小明进行了六次实验,并将实验所得数据制成下表:
砝码的质
量m/g 0 50 100 150 200 250
滑动摩
擦力f/N 1.8 2.0 2.2 2.4 2.6 2.8
(1)通过观察上表,请确定f与m的关系式;
(2)在某次实验中,测得木块受到的摩擦力
为4.2 N,则此时砝码的质量是多少?
(3)在实验过程中,当砝码的质量为
100~800 g时,请直接写出木块受到的
摩擦力的最大值和最小值分别为多少?
解:(1)f与m的关系式为f=0.004m+1.8.
(2)当f=4.2时,0.004m+1.8=4.2,
解得m=600,∴此时砝码的质量是600 g.
(3)∵f随m的增大而增大,
∴当m=800时,f值最大,此时f=5.0;
当m=100时,f值最小,此时f=2.2.
∴当砝码的质量为100 g~800 g时,木块受到的摩擦力的最大值和最小值分别为5.0 N,2.2 N.
12.刹车系统是车辆行驶安全重要保障,某学习小组研究了刹车距离的影响因素.
反应距离:驾驶员从开始意识危险到踩下刹车的这段时间内,机动车所行驶的距离.
制动距离:驾驶员从踩下刹车开始到汽车完全停止的这段时间内,机动车所行驶的距离.
汽车急刹车的停车距离y(m)为反应距离y1(m)与制动距离y2(m)之和,即
y=y1+y2,而反应距离、制动距离均与汽车行驶的速度x (m/s) 有关,如图是学习小组利用电脑软件模拟出的相关实验数据.
速度x(m/s) 反应距离y1(m) 制动距离y2(m)
10 7.5 8
15 11.25 18
20 15 32
25 18.75 50
30 22.5 72
35 26.25 98
40 30 128
…
经学习小组信息收集得知,汽车的急刹车距离还与汽车本身刹车系数k有关,且满足 y=y1+k·y2,并且不同类型汽车的刹车系数k满足 0.8≤k≤1.5.
(1)请利用表格中的数据,分别计算y1,y2与x的函数关系式;
(2)在某条限速为60 km/h的道路上,一辆轿车为避险采取急刹车,通过交警判断该车此次急刹车过程的制动距离为34 m,请你利用(1)中的函数关系式,判断该车是否超速?
(3)某条新建道路要求所有类型的汽车在急刹车时的停车距离至多15 m,试问汽车在该条道路的行驶速度应该限速多少?(精确到1 m/s)
13.如图①是1个纸杯和4个叠放在一起的纸杯的示意图,为了探究叠在一起的纸杯的总高度H(cm)随着纸杯数量x(个)的变化规律.设纸杯底部到纸杯沿底边高为h(cm),杯沿高为a cm.
(1)写出纸杯的总高度H(cm)与纸杯数量x(个)的函数关系式: (用含a,h的式子表示);
H=h+ax
(2)小琪同学经过实践探究,列出下列表格:
纸杯数量x(单位:个) 3 6
纸杯总高度H(单位:cm) 9.5 14
Ⅰ)根据表格中数据求出h和a的值;
Ⅱ)该型号纸杯有15个装、20个装、25个装共三种包装,均把纸杯叠放成一叠进行包装,图②是某品牌饮水机的示意图,储藏柜的高度是40 cm.则该储藏柜能放得下(杯口向上)这三种包装中哪些包装的纸杯(直接写结果).
14.综合与实践课上,数学王老师分发给每位同学若干张相同的长方形纸片.王老师取出三张纸片演示操作,依次将纸片沿事先画出的竖直和水平方向的实线裁剪成若干个完全相同的小长方形.
(1)请补全下面表格,试写出裁剪得到的小长方形个数m与纸片序号n之间的函数关系式为 5 ;
m=n2+n
纸片序号n 1 2 3 4 5
裁剪得到的小长
方形个数m 2 6 12 5 5
20
30
(2)某农科研究所有一块矩形的耕地ABCD,AB=40 m,BC=35 m,现需要将其分成若干小长方形耕地,进行不同种子的育种实验.按照上图中的分割方式,爱思考的同学提出以下2个问题.
Ⅰ)若将此耕地分成56个完全相同的小长方形耕地,求竖直方向分割用的实线数量;
Ⅱ)为了方便科研人员观察并收集实验数据,将竖直和水平方向的实线换成1 m宽的小路,若小路的面积之和占此耕地面积的36%,求小长方形耕地的总数量.
解:(2)Ⅰ)由题意得n(n+1)=56,
∵n为正整数,∴n=7,
∴竖直方向分割用的实线数量为7.
Ⅱ)设水平方向有n条道路,竖直方向有(n+1)条道路,由题意得
40n+35(n+1)-n(n+1)=40×35×36%,整理得n2-74n+469=0,
解得n=7或n=67(舍去),水平方向耕地数量为8,竖直方向耕地数量为9,
∴耕地块数为8×9=72(块).
∴小长方形耕地的总数量为72块.
类型一:几何模型迁移综合实践型
1.(2024·宁夏第25题10分)综合与实践
如图①,在△ABC中,BD是∠ABC的平分线,BD的延长线交∠CAM的平分线于点E.
【发现结论】
结论1:∠AEB= _∠ACB;
结论2:当图①中∠ACB=90°时,
如图②,延长BC交AE于点F,过点E作AF的垂线交BF于点G,交AC的延长线于点H.则AE与EG的数量关系是 ;
AE=EG
【应用结论】
(1)求证:AH=GF;
证明:(1)在Rt△AFC中,∠EFG+∠EAH=90°,
在Rt△AEH中,∠AHE+∠EAH=90°,
∴∠EFG=∠EHA,
又∵∠FEG=∠AEH,EG=EA,
∴△EFG≌△EHA(AAS),∴AH=GF.
第1课时 “a=b”型的线段问题
“
a=b”型
(1)若a与b分别在不同的三角形中,
则直接证明对应所在三角形全等.
(2)若a与b不共线但共顶点,则证明所在三角形是等腰三角形.
(3)若a与b共线且共顶点,常用证明方法是作平行线,先构造一组三
角形全等得到一组对应边相等,再证明“8”字三角形全等(如图①).
需要证明:BD=DC.过点C作CF∥AB交ED的延长线于点F.
先构造一组三角形全等,得到对应边相等,即BE=CF或ED=DF,
再构造“8”字三角形△BED≌△CFD,得到BD=DC.
(4)若a与b垂直,常用证明方法是构造直角三角形,证明最大的三角形是等腰直角三角形,利用斜边的中点可得结论(如图②).
需要证明:BA=BC.
延长AB到点D,使得AB=BD,连接AC,DC.
先利用旋转型或双垂直型模型证明△ACD是直角三角形,
再利用斜边上的中点得到BA=BC.
在△ABC中,∠CAB=45°,BD⊥AC交AC于点D,点F在AB边上,CF交BD于点E.
(1)如图①,作FG⊥AC于点G,若E是CF的中点,∠CFB=75°,DE=1,补全图形,求AB的长;
(2)如图②,取BD的中点G,连接FG,若E是CF的中点,F是AB的中点,补全图形,求证:CF=CB.
【方法总结】证明两条线段相等,除了构造三角形全等,还可以证明它是等腰三角形或者利用等腰三角形三线合一的方法来证明.
1.如图,在△ABC中,AB=AC,∠BAC=90°.
【发现结论】
(1)当BD平分∠ABC交AC于点D,F为BC上一点,连接AF交BD于点E.
结论1:若AB=BF,则∠BEF= 5 ;
结论2:如图①,若AF⊥BD,过点C作CM⊥AF交AF的延长线于点M,则AD与CF的数量关系是 5 ;
90°
AD=CF
①
【应用结论】
(2)如图②,BD平分∠ABC交AC于点D,CE⊥BD,垂足E在BD的延长线上.延长BA,CE相交于点F,试判断线段CE和BD的数量关系,并说明理由;
解:(2)BD=2CE.
理由:∵BD平分∠ABC,∴∠ABD=∠CBD,
∴△BCE≌△BFE(ASA),∴CE=EF,
∵∠BAC=90°,CE⊥BD,
∴∠ACF+∠F=90°,∠ABD+∠F=90°,
∴∠ABD=∠ACF,∴△ABD≌△ACF(ASA),
∴BD=CF,∵CF=CE+EF=2CE,∴BD=2CE.
②
2.【模型启迪】
(1)如图①,在△ABC中,D为BC边的中点,连接AD并延长至点H.使DH=AD,连接CH.由∠ADB=∠CDH,得△ADB≌△HDC,则AB与CH的数量关系为 ,位置关系为 ;
AB=CH
AB∥CH
【模型探索】
(2)如图②,在△ABC中,AP平分∠BAC,D为BC边的中点,过点D作DQ∥AP,交CA的延长线于点Q,交AB边于点K,作BH∥CQ,交QD的延长线于点H,试判断BK与CQ的数量关系,并说明理由;
(2)解:BK=CQ,理由:由题意得∠H=∠Q,
∵DQ∥AP,∴∠Q=∠CAP,∠BKH=∠BAP,
∴∠H=∠CAP,∵AP平分∠BAC,∴∠CAP=∠BAP,
∴∠H=∠BKH,∴BK=BH,∵D为BC边的中点,
∴BD=CD,∵∠BDH=∠CDQ,∴△BDH≌△CDQ(AAS),
∴BH=CQ,∴BK=CQ.
(3)如图③,在△ABC中,D为BC的中点,连接AD,E为AC边上一点,过点E作EG⊥AD于点G,连接BE交AD于点F,且BF=AC.作BR∥AC,交AD的延长线于点R,补全图形,求证:AG=GF.
(3)证明:由题意得∠R=∠CAD,
∵D为BC的中点,∴BD=CD,
∵∠RDB=∠ADC,∴△RDB≌△ADC(AAS),
∴RB=AC,∵BF=AC,∴RB=BF,∴∠R=∠BFR,
∴∠BFR=∠CAD,∴∠AFE=∠BFR=∠CAD,
∴AE=FE,∵EG⊥AD,∴AG=GF.
第2课时 “a=b+c”型的线段和差问题
针对几何题目中涉及三条线段之间的和、差关系(a=b+c),我们一般采用截长补短或类似截长补短的方法.
1.截长补短法
有一类几何题,其命题主要是证明三条线段长度的“和”或“差”或比例关系,一般可以采取截长或补短的方法进行求解,所谓“截长”,就是将三者中最长的那条线段一分为二,使其中的一条线段与已知线段相等,然后证明其中的另一条线段与已知的另一条线段的大小关系,所谓“补短”,就是将一条已知的较短的线段延长,延长部分与另一条已知的较短的线段的长度相等,然后求出延长后的线段与最长的已知线段的大小关系.有的是采取截长补短的方法后,使之构成某种特定的三角形进行求解.
(1)截长法:①过某一点作长边的垂线;②在长边截取一条与某一短边相等的线段,再证剩下的线段与另一短边相等.
(2)补短法:①延长短边;②通过旋转等方式使两短边拼合在一起.
2.类似截长补短
这类几何题主要是借助题目给出的条件,如角平分线,等腰三角形等作出类似于截长补短的辅助线求解.
(2024·银川区模拟)已知△ABC是等边三角形.
(1)如图①,若AB=4,点D在线段BC上,且BD=1,连接AD,过点D作DE⊥AB于点E,请补全图形,求AD的长;
(2)如图②,E是BC延长线上一点,∠AEF=60°,EF交△ABC的外角平分线于点F,在线段CF上截取一点G,使得CG=CE,连接EG,请补全图形,求证:CF=AC+CE.
(2)证明:∵△ABC是等边三角形,∴∠ACB=60°,
∴∠ACE=180°-∠ACB=120°,
∵CF平分∠ACE,∴∠ACF=∠ECF=60°,
∴△CEG是等边三角形,∴CE=GE,
∠CEG=∠CGE=60°=∠AEF,
∴∠FGE=∠ACE=120°,∠CEA=∠GEF,
∴△ACE≌△FGE(ASA),∴AC=FG,∴CF=CG+GF=AC+CE.
【方法归纳】根据问题的特征“a=b+c”,可以快速判断是否采用截长补短法,关键是在进行截长或补短后,是否可以证明三角形全等,或者是否为等腰三角形,是判断方法是否准确的重要评判手段.
3.【问题背景】如图①,已知AM∥BN,AE平分∠BAM,BE平分∠ABN,过点E的直线交射线AM于点C,交射线BN于点D.探究图中AC,BD,AB之间的数量关系.
(1)小王同学探究此问题的方法是:延长AE交BN于点F,先证∠AEB=90°,说明△ABE≌△FBE,再证△ACE≌△FDE,可得出结论: ;
AB=BD+AC
【探索延伸】如图②,已知AM∥BN,AE平分∠BAM,BE平分∠ABN,过点E的直线交射线AM的反向延长线于点C,交射线BN于点D.延长AE交BD于点G.
(2)试判断AC,BD与AB之间的数量关系,并说明理由;
(3)若AB=5,AC=3,S△ABE-S△ACE=4,
求S△BDE.
4.【模型建立】
如图,在正方形ABCD中,E,F分别是BC,CD边上的点
(点E不与点B,C重合),且∠EAF=45°.
(1)当BE=DF时,求证:AE=AF;
【模型应用】
(2)在CD的延长线上截取DM=BE,
猜想BE,EF,DF三条线段之间存在的数量关系,并证明;
【模型迁移】
(3)连接AC,G是CB延长线上一点,GH⊥AE,垂足为K,交AC于点H且GH=AE.作HR⊥BC于点R,若DF=a,CH=b,补全图形,请用含a,b的代数式表示EF的长
(1)证明:由题意得AB=AD,∠B=∠D=90°,BE=DF,
∴△ABE≌△ADF(SAS),∴AE=AF.
(2)解:BE+DF=EF,
证明:易证△ABE≌△ADM(SAS),∴∠BAE=∠DAM,AM=AE,
∵四边形ABCD是正方形,∴∠BAD=90°,∵∠EAF=45°,
∴∠BAE+∠DAF=45°,∴∠DAM+∠DAF=45°,即∠MAF=45°,
∴∠MAF=∠EAF,∴△MAF≌△EAF(SAS),∴FM=FE,
∴DM+DF=EF,∴BE+DF=EF.
证明与 有关的线段数量关系时,常通过构造等腰直角三角形解决问题.
(2)如图②,延长BD至点G,使AG=AC,作∠BAG的平分线交BD于点H,交GC的延长线于点K.过点A作AQ⊥AK交KB的延长线于点Q,请补全图形,求证:CK+GK=AK.
证明:(1)∵AC是正方形ABCD的对角线,
∴AB=AD,∠BAE=∠DAE=45°,
∴△ABE≌△ADE(SAS),∴BE=DE.
(2)∵四边形ABCD是正方形,∴∠GAD=90°,∴∠AGD+∠ADG=90°,
由(1)知△ABE≌△ADE,∴∠ADG=∠EBG,∴∠AGD+∠EBG=90°,
∵FB⊥BE,∴∠FBG+∠EBG=90°,∴∠AGD=∠FBG=∠FGB,
∴FG=FB.
6.【模型建立】
(1)如图①,△ABC和△BDE都是等边三角形,点C关于AD的对称点F在BD边上.
Ⅰ)求证:AE=CD;
Ⅱ)用等式写出线段AD,BD,DF的数量关系,
并说明理由;
(1)Ⅰ)证明:∵△ABC和△BDE都是等边三角形,
∴AB=BC,BE=BD,∠ABC=∠EBD=60°,
∴∠ABC-∠CBE=∠EBD-∠CBE,
∴∠ABE=∠CBD,∴△ABE≌△CBD(SAS),
∴AE=CD.
Ⅱ)解:AD=DF+BD.理由:∵△BDE是等边三角形,∴BD=DE.
∵点C与点F关于AD对称,∴CD=DF.由(1)知AE=CD,∴AE=DF.
∴AD=AE+DE=DF+BD.
【模型应用】
(2)如图②,△ABC是直角三角形,AB=AC,CD⊥BD,垂足为D,点C关于AD的对称点F在BD边上.过点B作BE⊥AD于点E,请补全图形,用等式写出线段AD,BD,DF的数量关系,并说明理由.
如图,在△ABC中,AB=AC,D是BC边上一点(点D不与端点重合).点D关于直线AB的对称点为点E,连接AD,DE.在直线AD上取一点F,使∠EFD=∠BAC,直线EF与直线AC交于点G.
(1)若∠BAC=60°,BD<CD,∠BAD=α,求∠AGE的度数(用含α的代数式表示);
(2)若∠BAC=60°,BD<CD,在CG上截取
CM=BD,连接BM,BE,AE,BM交AD于点H,
补全图形,用等式表示线段CG与DE之间的数量
关系,并证明.
解:(1)由题可得∠EFD=∠BAC=60°,
∵∠EFD=∠1+∠BAD=∠1+α,
∴∠1=60°-α,∵∠AGE+∠1+∠BAC=180°,
∴∠AGE=180°-60°-∠1=120°-∠1,
∴∠AGE=120°-(60°-α)=60°+α.
【方法归纳】在等边三角形中有垂直或有中点(中线),观察图形的形状,猜倍的关系,去证明是含30°的直角三角形.
类型二:数学文化迁移综合实践型
(2023T26,2022T26)
2.(2023·宁夏第26题10分)综合与实践
【问题背景】
数学小组发现国旗上五角星的五个角都是
顶角为36°的等腰三角形,对此三角形产生
了极大兴趣并展开探究.
【探究发现】
如图①,在△ABC中,∠A=36°,AB=AC.
(1)操作发现:将△ABC折叠,使边BC落在边BA上,点C的对应点是点E,折痕交AC于点D,连接DE,DB,则∠BDE= ,设AC=1,BC=x,那么AE= (用含x的式子表示);
72°
1-x
【拓展应用】
当等腰三角形的底与腰的比等于黄金比时,这个三角形叫黄金三角形.例如,图①中的△ABC是黄金三角形.
(3)如图②,在菱形ABCD中,∠BAD=72°,AB=1.求这个菱形较长对角线的长.
【拓展应用】
(3)如图③,在△ABC中, D为AB边上的一点(不与A, B重合),过点D作DE∥BC,交AC于点E,BE,CD相交于点F,连接AF并延长,与DE,BC分别交于M,N.请问直线AN是△ABC的黄金分割线吗?并说明理由.
10.(2024·同心县模拟)
(1)阅读理解
我国是最早了解勾股定理的国家之一,它被记载于我国古代的数学著作《周髀算经》中.汉代数学家赵爽为了证明勾股定理,创制了一幅如图①所示的“弦图”,后人称之为“赵爽弦图”.根据“赵爽弦图”写出勾股定理: 5 ;
a2+b2=c2
(2)问题解决
勾股定理的证明方法有很多,如图②是古代的一种证明方法:过正方形
ACDE的中心O,作FG⊥HP,将它分成4份,所分成的四部分和以BC为边的正方形恰好能拼成以AB为边的正方形.
若AC=12,BC=5,求EF的值;
(3)拓展探究
如图③,以正方形一边为斜边向外作直角三角形,再以该直角三角形的两直角边分别向外作正方形,重复这一过程就可以得到“勾股树”的部分图形.设大正方形N的边长为定值n,小正方形
A,B,C,D的边长分别为a,b,c,d.已知
∠1=∠2=∠3=α,当角α(0°<α<90°)变化
时,探究b与c的关系式,并写出该关系式及
解答过程(b与c的关系式用含n的式子表示).
类型三:与函数有关的综合实践型
(2020T25,2019T25)
3.(2020·宁夏第25题10分)在综合与实践活动中,活动小组的同学看到网上购鞋的鞋号(为正整数)与脚长(mm)的对应关系如表1:
鞋号
(正整数) 22 23 24 25 26 27 …
脚长
(mm) 160±2 165±2 170±2 175±2 180±2 185±2 …
为了方便对问题的研究,活动小组将表1中的数据进行了编号,并对脚长的数据bn定义为[bn].如表2:
序号n 1 2 3 4 5 6 …
鞋号an 22 23 24 25 26 27 …
脚长bn 160±2 165±2 170±2 175±2 180±2 185±2 …
脚长
[bn] 160 165 170 175 180 185 …
定义:对于任意正整数m,n,其中m>2.若[bn]=m,则m-2≤bn≤m+2.
如:[b4]=175表示175-2≤b4≤175+2,即173≤b4≤177.
(1)通过观察表2,猜想出an与序号n之间的关系式,[bn]与序号n之间的关系式;
(2)用含an的代数式表示[bn];计算鞋号为42的鞋适合的脚长范围;
(3)若脚长为271 mm,那么应购鞋的鞋号为多大?
解:(1)an=21+n;
[bn]=160+5(n-1)=5n+155.
(2)由an=21+n与[bn]=5n+155得
[bn]=5an+50,把an=42代入an=21+n得
n=21,∴[b21]=5×42+50=260,
则260-2≤b21≤260+2,即258≤b21≤262.
答:鞋号为42的鞋适合的脚长范围是258 mm~262 mm
(3)根据[bn]=5n+155可知[bn]能被5整除,
∵270-2≤271≤270+2,∴[bn]=270,
将[bn]=270代入[bn]=5an+50中得an=44.
故应购买44号的鞋.
4.(2019·宁夏第25题10分)在综合与实践活动中,活动小组对学校400 m的跑道进行规划设计.如图,跑道由两段直道和两端是半圆弧的跑道组成,其中400 m跑道最内圈为400 m,两端半圆弧的半径为36 m.(π取3.14)
(1)求400 m跑道中一段直道的长度;
(2)在活动中发现跑道周长(单位:m)随跑道宽度(距最内圈的距离,单位:m)的变化而变化.请完成下表:
跑道
宽度(m) 0 1 2 3 4 5 …
跑道
周长(m) 400 5 5 5 5 5 …
406.28
412.56
418.84
425.12
431.4
若设x表示跑道宽度(单位:m),y表示该跑道周长(单位:m),试写出y与x的函数解析式;
(3)将446 m的跑道周长作为400 m跑道场地的最外沿,那么它与最内圈(跑道周长400 m)形成的区域最多能铺设道宽为1.2 m 的跑道多少条?
解:(1)400 m跑道中一段直道的长度为
(400-2×36×3.14)÷2
=86.96(m).
(2)补充表格如表所示.
y与x的函数解析式为y=6.28x+400.
(3)当y=446时,即6.28x+400=446,
解得 x≈7.32,7.32÷1.2≈6 (条).
答:最多能铺设道宽为1.2 m的跑道6条.
11.通过学习我们知道,在水平面上推或拉一个物体时,在物体和水平面之间会产生阻碍物体运动的力,像这样的力是摩擦力.小明利用如图所示的装置测量在不同重量下某木块与木板之间的摩擦力.在木块上放置砝码,缓慢向左拉动水平放置的木板,当木块和砝码相对桌面静止且木板仍在继续滑动时,弹簧秤的示数即为木块受到的摩擦力的大小.小明进行了六次实验,并将实验所得数据制成下表:
砝码的质
量m/g 0 50 100 150 200 250
滑动摩
擦力f/N 1.8 2.0 2.2 2.4 2.6 2.8
(1)通过观察上表,请确定f与m的关系式;
(2)在某次实验中,测得木块受到的摩擦力
为4.2 N,则此时砝码的质量是多少?
(3)在实验过程中,当砝码的质量为
100~800 g时,请直接写出木块受到的
摩擦力的最大值和最小值分别为多少?
解:(1)f与m的关系式为f=0.004m+1.8.
(2)当f=4.2时,0.004m+1.8=4.2,
解得m=600,∴此时砝码的质量是600 g.
(3)∵f随m的增大而增大,
∴当m=800时,f值最大,此时f=5.0;
当m=100时,f值最小,此时f=2.2.
∴当砝码的质量为100 g~800 g时,木块受到的摩擦力的最大值和最小值分别为5.0 N,2.2 N.
12.刹车系统是车辆行驶安全重要保障,某学习小组研究了刹车距离的影响因素.
反应距离:驾驶员从开始意识危险到踩下刹车的这段时间内,机动车所行驶的距离.
制动距离:驾驶员从踩下刹车开始到汽车完全停止的这段时间内,机动车所行驶的距离.
汽车急刹车的停车距离y(m)为反应距离y1(m)与制动距离y2(m)之和,即
y=y1+y2,而反应距离、制动距离均与汽车行驶的速度x (m/s) 有关,如图是学习小组利用电脑软件模拟出的相关实验数据.
速度x(m/s) 反应距离y1(m) 制动距离y2(m)
10 7.5 8
15 11.25 18
20 15 32
25 18.75 50
30 22.5 72
35 26.25 98
40 30 128
…
经学习小组信息收集得知,汽车的急刹车距离还与汽车本身刹车系数k有关,且满足 y=y1+k·y2,并且不同类型汽车的刹车系数k满足 0.8≤k≤1.5.
(1)请利用表格中的数据,分别计算y1,y2与x的函数关系式;
(2)在某条限速为60 km/h的道路上,一辆轿车为避险采取急刹车,通过交警判断该车此次急刹车过程的制动距离为34 m,请你利用(1)中的函数关系式,判断该车是否超速?
(3)某条新建道路要求所有类型的汽车在急刹车时的停车距离至多15 m,试问汽车在该条道路的行驶速度应该限速多少?(精确到1 m/s)
13.如图①是1个纸杯和4个叠放在一起的纸杯的示意图,为了探究叠在一起的纸杯的总高度H(cm)随着纸杯数量x(个)的变化规律.设纸杯底部到纸杯沿底边高为h(cm),杯沿高为a cm.
(1)写出纸杯的总高度H(cm)与纸杯数量x(个)的函数关系式: (用含a,h的式子表示);
H=h+ax
(2)小琪同学经过实践探究,列出下列表格:
纸杯数量x(单位:个) 3 6
纸杯总高度H(单位:cm) 9.5 14
Ⅰ)根据表格中数据求出h和a的值;
Ⅱ)该型号纸杯有15个装、20个装、25个装共三种包装,均把纸杯叠放成一叠进行包装,图②是某品牌饮水机的示意图,储藏柜的高度是40 cm.则该储藏柜能放得下(杯口向上)这三种包装中哪些包装的纸杯(直接写结果).
14.综合与实践课上,数学王老师分发给每位同学若干张相同的长方形纸片.王老师取出三张纸片演示操作,依次将纸片沿事先画出的竖直和水平方向的实线裁剪成若干个完全相同的小长方形.
(1)请补全下面表格,试写出裁剪得到的小长方形个数m与纸片序号n之间的函数关系式为 5 ;
m=n2+n
纸片序号n 1 2 3 4 5
裁剪得到的小长
方形个数m 2 6 12 5 5
20
30
(2)某农科研究所有一块矩形的耕地ABCD,AB=40 m,BC=35 m,现需要将其分成若干小长方形耕地,进行不同种子的育种实验.按照上图中的分割方式,爱思考的同学提出以下2个问题.
Ⅰ)若将此耕地分成56个完全相同的小长方形耕地,求竖直方向分割用的实线数量;
Ⅱ)为了方便科研人员观察并收集实验数据,将竖直和水平方向的实线换成1 m宽的小路,若小路的面积之和占此耕地面积的36%,求小长方形耕地的总数量.
解:(2)Ⅰ)由题意得n(n+1)=56,
∵n为正整数,∴n=7,
∴竖直方向分割用的实线数量为7.
Ⅱ)设水平方向有n条道路,竖直方向有(n+1)条道路,由题意得
40n+35(n+1)-n(n+1)=40×35×36%,整理得n2-74n+469=0,
解得n=7或n=67(舍去),水平方向耕地数量为8,竖直方向耕地数量为9,
∴耕地块数为8×9=72(块).
∴小长方形耕地的总数量为72块.
同课章节目录
