中考数学复习专项突破重难题型八 课件(共57张PPT)
文档属性
| 名称 | 中考数学复习专项突破重难题型八 课件(共57张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 8.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-03-30 13:22:11 | ||
图片预览








文档简介
(共57张PPT)
重难题型八 二次函数与几何综合
——三阶 综合提升练
类型一:二次函数与线段问题
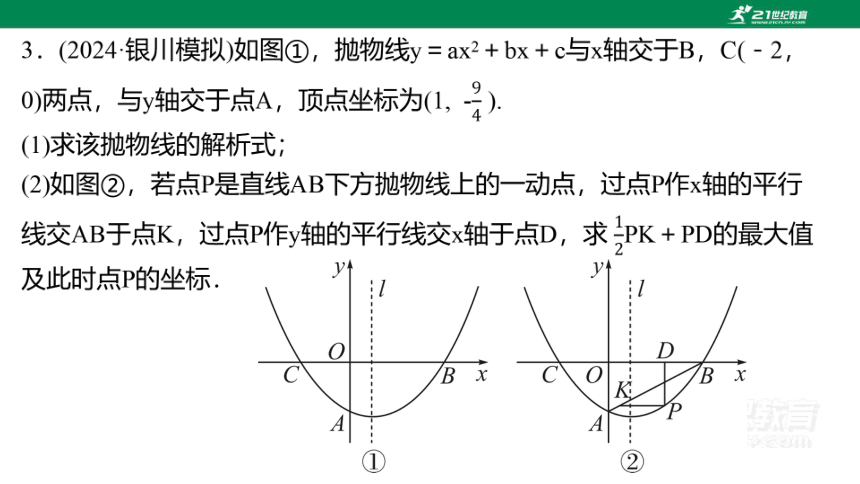
1.(2024·临夏州节选)在平面直角坐标系中,抛物线y=-x2+bx+c与x轴交于A(-1,0),B(3,0)两点,与y轴交于点C,作直线BC.
(1)求抛物线的解析式;
(2)如图,P是线段BC上方的抛物线上一动点,
过点P作PQ⊥BC,垂足为Q,请问线段PQ
是否存在最大值?若存在,请求出最大值及
此时点P的坐标;若不存在请说明理由.
解:(1)由题意知
y=-(x+1)(x-3),
∴y=-x2+2x+3.
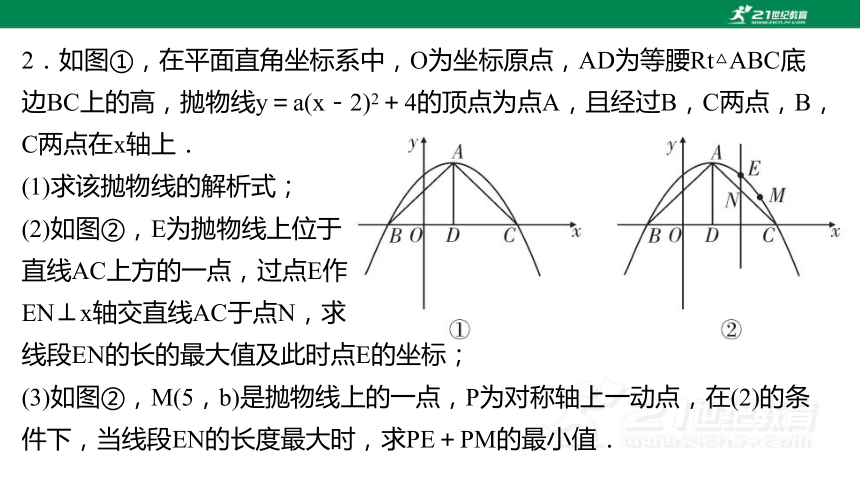
2.如图①,在平面直角坐标系中,O为坐标原点,AD为等腰Rt△ABC底边BC上的高,抛物线y=a(x-2)2+4的顶点为点A,且经过B,C两点,B,C两点在x轴上.
(1)求该抛物线的解析式;
(2)如图②,E为抛物线上位于
直线AC上方的一点,过点E作
EN⊥x轴交直线AC于点N,求
线段EN的长的最大值及此时点E的坐标;
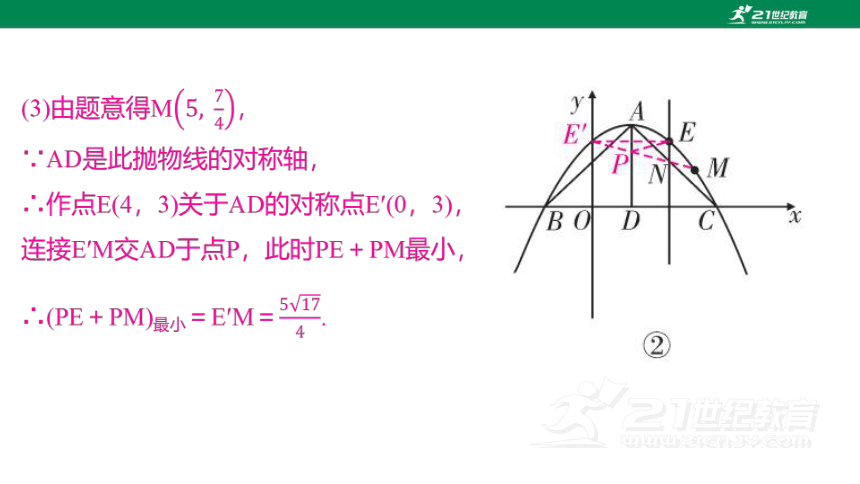
(3)如图②,M(5,b)是抛物线上的一点,P为对称轴上一动点,在(2)的条件下,当线段EN的长度最大时,求PE+PM的最小值.
类型二:二次函数与面积问题
5.(2024·西吉县模拟)如图,已知二次函数y=x2+bx+c的图象与x轴交于A, B两点,其中点 A坐标为(-3,0),与y轴交于点C,点D(-2,-3)在抛物线上.
(1)求抛物线的解析式;
(2)抛物线的对称轴上有一动点P,
求出PA+PD的最小值;
(3)若抛物线上有一动点E,使△ABE的面积为6,
求点E坐标.
6.如图,已知抛物线y=ax2+bx+3与x轴交于A(-1,0),B(3,0)两点,与y轴交于点C,连接BC.
(1)求抛物线的解析式;
(2)若P为线段BC上的一动点(不与B,C重合),
PM∥y轴,且PM交抛物线于点M,交x轴于点N,
当△BCM的面积最大时,求点P 的坐标.
7.(2024·凉山州)如图,抛物线y=-x2+bx+c与直线y=x+2相交于
A(-2,0),B(3,m)两点,与x轴相交于另一点C.
(1)求抛物线的解析式;
(2)抛物线上是否存在点M,使△ABM的
面积等于△ABC面积的一半?若存在,
请直接写出点M的坐标;若不存在,
请说明理由.
8.(2024·惠农区模拟)在平面直角坐标系中,二次函数y=ax2+bx+2的图象与x轴交于A(-3,0),B(1,0)两点,与y轴交于点C.P是抛物线上任意一点,连接PA,PC.
(1)求这个抛物线与直线AC的解析式;
(2)如图,过P,B作直线BP,交直线AC于点Q,
是否存在一点P,使得S△PQC∶S△BQC=1∶2,若
存在,直接写出点P的横坐标;若不存在,
请说明理由.
类型三:二次函数与特殊三角形问题
9.如图,二次函数y=ax2+bx+c(a≠0)的图象与x轴分别交于A(-1,0),B(3,0)两点,与y轴交于点C(0,-3),P,Q为抛物线上的两点.
(1)求二次函数的解析式;
(2)当P,C两点关于抛物线对称轴对称,
△OPQ是以点P为直角顶点的直角三角形
时,求点Q的坐标.
10.(2024·达州节选)如图,抛物线y=ax2+kx-3与x轴交于点A(-3,0)和点B(1,0),与y轴交于点C.D是抛物线的顶点.
(1)求抛物线的解析式;
(2)若N是抛物线对称轴上位于点D上方的一动点,
是否存在以点N,A,C为顶点的三角形是等腰
三角形,若存在,请直接写出满足条件的点N的
坐标;若不存在,请说明理由.
11.如图,在平面直角坐标系xOy中,已知抛物线y=ax2+c经过P(4,
-3),与y轴交于点A(0,1),直线y=kx(k≠0)与抛物线交于B,C两点.
(1)求抛物线的函数解析式;
(2)若△ABP是以AB为腰的等腰三角形,求点B的坐标.
12.如图,在平面直角坐标系中,抛物线y=ax2+bx+c与x轴交于B(4,0),C(-2,0)两点,与y轴交于点A(0,-2).
(1)求该抛物线的函数解析式;
(2)在抛物线的对称轴上是否存在一点M,使得△MAB是以AB为一条直角边的直角三角形;若存在,请求出点M的坐标,若不存在,请说明理由.
类型四:二次函数与特殊四边形问题
13.(2024·泸州)如图,在平面直角坐标系xOy中,已知抛物线y=ax2+bx+3经过点A(3,0),与y轴 交于点B,且关于直线x=1对称.
(1)求该抛物线的解析式;
(2)C是抛物线上位于第一象限的一个动点,
过点C作x轴的垂线交直线AB于点D,在y轴上
是否存在点E,使得以B,C,D,E为顶点的
四边形是菱形?若存在,求出该菱形的边长;
若不存在,说明理由.
16.如图,在平面直角坐标系中,抛物线y=x2+bx+c经过A(3,0),B(0,-3)两点,P是直线AB上一动点,过点P作x轴的垂线交抛物线于点M,交x轴于点N.
(1)分别求直线AB和这条抛物线的解析式;
(2)C是平面直角坐标系中的一点,当点M在
第四象限时,是否存在这样的点M,使得以
A,C,B,M为顶点组成的以AB为边的矩形?
若存在,求点C的坐标;若不存在,请说明理由.
解:(1)直线AB的解析式为y=x-3,抛物线的解析式为y=x2-2x-3.
(2)存在.设M(m,m2-2m-3),AB2=18,
AM2=(m-3)2+(m2-2m-3)2,BM2=m2+(m2-2m)2,
①当AB2+AM2=BM2时,
即18+(m-3)2+(m2-2m-3)2=m2+(m2-2m)2,∴m2-m-6=0,
解得m=-2或m=3(舍去),∴M(-2,5)(不在第四象限,舍去);
②AB2+BM2=AM2时,即18+m2+(m2-2m)2=(m-3)2+(m2-2m-3)2,整理得m2-m=0,而m≠0,∴m=1,∴M(1,-4),
∵四边形ABMC是矩形,∴C(4,-1).综上所述,C(4,-1).
类型五:二次函数与角度问题
17.(2024·海南)如图,抛物线y=-x2+bx+4经过点A(-4,0),B(1,0),交y轴于点C(0,4),P是抛物线上一动点.
(1)求该抛物线的函数解析式;
(2)当点P的坐标为(-2,6)时,
求四边形AOCP的面积;
(3)当∠PBA=45°时,求点P的坐标.
解:(1)抛物线的函数解析式为y=-x2-3x+4.
(2)由点A,C的坐标得直线AC的解析式为y=x+4,连接AC,
过点P作PH∥y轴交AC于点H(-2,2),则PH=6-2=4,
∴S四边形AOCP=S△APC+S△AOC=16.
(3)当∠PBA=45°时,则直线BP的解析式为
y=±(x-1),联立上式和抛物线的解析式得
-x2-3x+4=x-1或-x+1=-x2-3x+4,
解得x=-5,-3或1(舍去).
故点P的坐标为(-5,-6)或(-3,4).
18.抛物线y=ax2+bx+3与x轴交于A(-3,0),B(1,0)两点,与y轴交于点C.
(1)求抛物线的解析式;
(2)如图,连接BC,在抛物线上求出点Q,
使∠QAC+∠OCB=45°.
重难题型八 二次函数与几何综合
——三阶 综合提升练
类型一:二次函数与线段问题
1.(2024·临夏州节选)在平面直角坐标系中,抛物线y=-x2+bx+c与x轴交于A(-1,0),B(3,0)两点,与y轴交于点C,作直线BC.
(1)求抛物线的解析式;
(2)如图,P是线段BC上方的抛物线上一动点,
过点P作PQ⊥BC,垂足为Q,请问线段PQ
是否存在最大值?若存在,请求出最大值及
此时点P的坐标;若不存在请说明理由.
解:(1)由题意知
y=-(x+1)(x-3),
∴y=-x2+2x+3.
2.如图①,在平面直角坐标系中,O为坐标原点,AD为等腰Rt△ABC底边BC上的高,抛物线y=a(x-2)2+4的顶点为点A,且经过B,C两点,B,C两点在x轴上.
(1)求该抛物线的解析式;
(2)如图②,E为抛物线上位于
直线AC上方的一点,过点E作
EN⊥x轴交直线AC于点N,求
线段EN的长的最大值及此时点E的坐标;
(3)如图②,M(5,b)是抛物线上的一点,P为对称轴上一动点,在(2)的条件下,当线段EN的长度最大时,求PE+PM的最小值.
类型二:二次函数与面积问题
5.(2024·西吉县模拟)如图,已知二次函数y=x2+bx+c的图象与x轴交于A, B两点,其中点 A坐标为(-3,0),与y轴交于点C,点D(-2,-3)在抛物线上.
(1)求抛物线的解析式;
(2)抛物线的对称轴上有一动点P,
求出PA+PD的最小值;
(3)若抛物线上有一动点E,使△ABE的面积为6,
求点E坐标.
6.如图,已知抛物线y=ax2+bx+3与x轴交于A(-1,0),B(3,0)两点,与y轴交于点C,连接BC.
(1)求抛物线的解析式;
(2)若P为线段BC上的一动点(不与B,C重合),
PM∥y轴,且PM交抛物线于点M,交x轴于点N,
当△BCM的面积最大时,求点P 的坐标.
7.(2024·凉山州)如图,抛物线y=-x2+bx+c与直线y=x+2相交于
A(-2,0),B(3,m)两点,与x轴相交于另一点C.
(1)求抛物线的解析式;
(2)抛物线上是否存在点M,使△ABM的
面积等于△ABC面积的一半?若存在,
请直接写出点M的坐标;若不存在,
请说明理由.
8.(2024·惠农区模拟)在平面直角坐标系中,二次函数y=ax2+bx+2的图象与x轴交于A(-3,0),B(1,0)两点,与y轴交于点C.P是抛物线上任意一点,连接PA,PC.
(1)求这个抛物线与直线AC的解析式;
(2)如图,过P,B作直线BP,交直线AC于点Q,
是否存在一点P,使得S△PQC∶S△BQC=1∶2,若
存在,直接写出点P的横坐标;若不存在,
请说明理由.
类型三:二次函数与特殊三角形问题
9.如图,二次函数y=ax2+bx+c(a≠0)的图象与x轴分别交于A(-1,0),B(3,0)两点,与y轴交于点C(0,-3),P,Q为抛物线上的两点.
(1)求二次函数的解析式;
(2)当P,C两点关于抛物线对称轴对称,
△OPQ是以点P为直角顶点的直角三角形
时,求点Q的坐标.
10.(2024·达州节选)如图,抛物线y=ax2+kx-3与x轴交于点A(-3,0)和点B(1,0),与y轴交于点C.D是抛物线的顶点.
(1)求抛物线的解析式;
(2)若N是抛物线对称轴上位于点D上方的一动点,
是否存在以点N,A,C为顶点的三角形是等腰
三角形,若存在,请直接写出满足条件的点N的
坐标;若不存在,请说明理由.
11.如图,在平面直角坐标系xOy中,已知抛物线y=ax2+c经过P(4,
-3),与y轴交于点A(0,1),直线y=kx(k≠0)与抛物线交于B,C两点.
(1)求抛物线的函数解析式;
(2)若△ABP是以AB为腰的等腰三角形,求点B的坐标.
12.如图,在平面直角坐标系中,抛物线y=ax2+bx+c与x轴交于B(4,0),C(-2,0)两点,与y轴交于点A(0,-2).
(1)求该抛物线的函数解析式;
(2)在抛物线的对称轴上是否存在一点M,使得△MAB是以AB为一条直角边的直角三角形;若存在,请求出点M的坐标,若不存在,请说明理由.
类型四:二次函数与特殊四边形问题
13.(2024·泸州)如图,在平面直角坐标系xOy中,已知抛物线y=ax2+bx+3经过点A(3,0),与y轴 交于点B,且关于直线x=1对称.
(1)求该抛物线的解析式;
(2)C是抛物线上位于第一象限的一个动点,
过点C作x轴的垂线交直线AB于点D,在y轴上
是否存在点E,使得以B,C,D,E为顶点的
四边形是菱形?若存在,求出该菱形的边长;
若不存在,说明理由.
16.如图,在平面直角坐标系中,抛物线y=x2+bx+c经过A(3,0),B(0,-3)两点,P是直线AB上一动点,过点P作x轴的垂线交抛物线于点M,交x轴于点N.
(1)分别求直线AB和这条抛物线的解析式;
(2)C是平面直角坐标系中的一点,当点M在
第四象限时,是否存在这样的点M,使得以
A,C,B,M为顶点组成的以AB为边的矩形?
若存在,求点C的坐标;若不存在,请说明理由.
解:(1)直线AB的解析式为y=x-3,抛物线的解析式为y=x2-2x-3.
(2)存在.设M(m,m2-2m-3),AB2=18,
AM2=(m-3)2+(m2-2m-3)2,BM2=m2+(m2-2m)2,
①当AB2+AM2=BM2时,
即18+(m-3)2+(m2-2m-3)2=m2+(m2-2m)2,∴m2-m-6=0,
解得m=-2或m=3(舍去),∴M(-2,5)(不在第四象限,舍去);
②AB2+BM2=AM2时,即18+m2+(m2-2m)2=(m-3)2+(m2-2m-3)2,整理得m2-m=0,而m≠0,∴m=1,∴M(1,-4),
∵四边形ABMC是矩形,∴C(4,-1).综上所述,C(4,-1).
类型五:二次函数与角度问题
17.(2024·海南)如图,抛物线y=-x2+bx+4经过点A(-4,0),B(1,0),交y轴于点C(0,4),P是抛物线上一动点.
(1)求该抛物线的函数解析式;
(2)当点P的坐标为(-2,6)时,
求四边形AOCP的面积;
(3)当∠PBA=45°时,求点P的坐标.
解:(1)抛物线的函数解析式为y=-x2-3x+4.
(2)由点A,C的坐标得直线AC的解析式为y=x+4,连接AC,
过点P作PH∥y轴交AC于点H(-2,2),则PH=6-2=4,
∴S四边形AOCP=S△APC+S△AOC=16.
(3)当∠PBA=45°时,则直线BP的解析式为
y=±(x-1),联立上式和抛物线的解析式得
-x2-3x+4=x-1或-x+1=-x2-3x+4,
解得x=-5,-3或1(舍去).
故点P的坐标为(-5,-6)或(-3,4).
18.抛物线y=ax2+bx+3与x轴交于A(-3,0),B(1,0)两点,与y轴交于点C.
(1)求抛物线的解析式;
(2)如图,连接BC,在抛物线上求出点Q,
使∠QAC+∠OCB=45°.
同课章节目录
