人教版2024—2025学年八年级下册数学期中考试全真模拟试卷(含答案)
文档属性
| 名称 | 人教版2024—2025学年八年级下册数学期中考试全真模拟试卷(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 496.0KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-03-30 00:00:00 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
人教版2024—2025学年八年级下册数学期中考试全真模拟试卷
考生注意:本试卷共三道大题,25道小题,满分120分,时量120分钟
第I卷
一、选择题(每题只有一个正确选项,每小题3分,满分30分)
1.要使二次根式有意义,则x的取值范围是( )
A.x≠9 B.x>9 C.x≤9 D.x≥9
2.下列运算正确的是( )
A. B.9
C.12 D. 6
3.下列各组数中,是勾股数的为( )
A.1,1, B.1.5,2,2.5 C.4,5,6 D.5,12,13
4.下列四组条件中,不能判定四边形ABCD是平行四边形的是( )
A.AB∥DC,AD=BC B.AB∥DC,AB=DC
C.AB∥DC,AD∥BC D.AB=DC,AD=BC
5.如图,四边形ABCD的对角线互相平分,要使它变为矩形,需要添加的条件是( )
A.AB=CD B.AD=BC C.AC=BD D.AB=BC
6.已知在Rt△ABC中,∠A=90°,AC=3,AB=4,则BC的长为( )
A. B.3 C.5或 D.5
7.“今有方池一丈,葭生其中央,出水一尺,引葭赴岸,适与岸齐.问:水深几何?”这是我国数学史上的“葭生池中”问题.即AC=5,DC=1,BD=BA,则BC=( )
A.8 B.10 C.12 D.13
8.已知a+b=﹣6,ab=7.则代数式的值为( )
A. B. C. D.
9.如图,在Rt△ABC中,∠ACB=90°,D是AB的中点,且∠ACD=30°,DE∥BC交AC于点E,BF⊥CD于点F,连接EF.若AC=2,则EF的长是( )
A.2 B. C.1 D.
10.已知,则代数式的值为( )
A. B. C. D.
二、填空题(6小题,每题3分,共18分)
11.已知菱形ABCD的两条对角线AC、BD的长分别是8cm和6cm.则菱形的面积为 cm2.
12.已知,则xy= .
13.若一个等腰三角形的腰长为10,底边长为12,则其底边上的高为 .
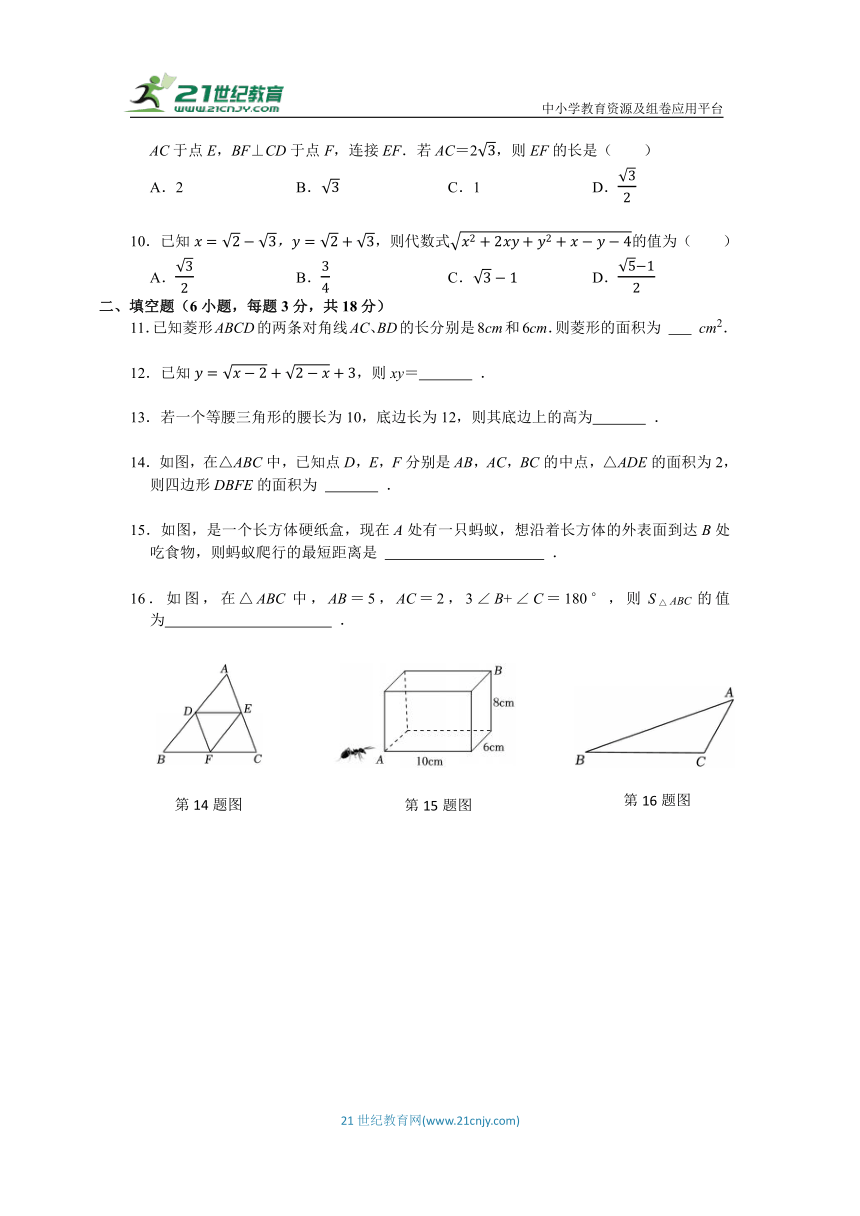
14.如图,在△ABC中,已知点D,E,F分别是AB,AC,BC的中点,△ADE的面积为2,则四边形DBFE的面积为 .
15.如图,是一个长方体硬纸盒,现在A处有一只蚂蚁,想沿着长方体的外表面到达B处吃食物,则蚂蚁爬行的最短距离是 .
16.如图,在△ABC中,AB=5,AC=2,3∠B+∠C=180°,则S△ABC的值为 .
第II卷
人教版2024—2025学年八年级下册数学期中考试全真模拟试卷
姓名:____________ 学号:____________准考证号:___________
一、选择题
题号 1 2 3 4 5 6 7 8 9 10
答案
二、填空题
11、_______ 12、______13、_______ 14、______15、_______ 16、______
三、解答题解答题(17、18、19题每题6分,20、21每题8分,22、23每题9分,24、25每题10分,共计72分,解答题要有必要的文字说明)
17.先化简,再求值:,其中.
18.计算:
(1); (2).
19.如图,方格纸中每个小正方形的边长为1、每个小正方形的顶点称为格点.已知△ABC的三个顶点都在格点上.
(1)判断△ABC的形状,并说明理由;
(2)求点B到AC的距离.
20.已知,,求下列代数式的值.
(1)a2+b2+2ab;
(2)a2﹣b2.
21.如图,在四边形ABCD中,∠B=90°,AB=BC=2,AD=1,CD=3.
(1)求∠DAB的度数.
(2)求四边形ABCD的面积.
22.台风是一种自然灾害,它在以台风中心为圆心,一定长度为半径的圆形区域内形成极端气候,有极强的破坏力.如图,监测中心监测到一台风中心沿监测点B与监测点A所在的直线由东向西移动,已知点C为一海港,且点C与A,B两点的距离分别为300km、400km,且∠ACB=90°,过点C作CE⊥AB于点E,以台风中心为圆心,半径为260km的圆形区域内为受影响区域.
(1)求监测点A与监测点B之间的距离;
(2)请判断海港C是否会受此次台风的影响,并说明理由;
(3)若台风的速度为25km/h,则台风影响该海港多长时间
23.将矩形ABCD折叠使A,C重合,折痕交BC于E,交AD于F.
(1)求证:四边形AECF为菱形;
(2)若AB=4,BC=8,求菱形的边长.
24.阅读下列材料,然后回答问题.
学习数学,最重要的是学习数学思想,其中一种数学思想叫做换元的思想,它可以简化我们的计算,比如我们熟悉的下面这个题:已知a+b=2,ab=﹣3,求a2+b2我们可以把a+b和ab看成是一个整体,令x=a+b,y=ab,则a2+b2=(a+b)2﹣2ab=x2﹣2y=4+6=10这样,我们不用求出a,b,就可以得到最后的结果.
(1)计算: , ;
(2)m是正整数,,且2a2+1955ab+2b2=2023,求m.
(3)已知,求的值.
25.如图,O为原点,四边形OABC为矩形,已知A(10,0),C(0,3),点D是OA的中点,动点P在线段BC上以每秒2个单位长的速度由点C向B运动.设动点P的运动时间为t秒.
(1)当t= 时,四边形PODB是平行四边形;
(2)在线段BC上是否存在一点Q,使得O,D,Q,P四点为顶点的四边形是菱形?若存在,求t的值,并求出Q点的坐标;若不存在,请说明理由;
(3)在线段PB上有一点M,且PM=5,求四边形OAMP周长的最小值.
参考答案
一、选择题
题号 1 2 3 4 5 6 7 8 9 10
答案 D D D A C D C A C C
1.【解答】解:由题意得:x﹣9≥0,
解得:x≥9,
故选:D.
2.【解答】解:A、 ,故此选项错误;
B、9993,故此选项错误;
C、2,故此选项错误;
D、 6,故此选项正确;
故选:D.
3.【解答】解:A、不是正整数,不是勾股数,不符合题意;
B、1.5,2.5不是正整数,不是勾股数,不符合题意;
C、42+52≠62,不是勾股数,不符合题意;
D、因为52+122=132,所以5,12,13是勾股数,符合题意.
故选:D.
4.【解答】解:A、∵AB∥CD,AD=BC,
∴四边形ABCD可能是平行四边形,有可能是等腰梯形.
故选项A不可以判断四边形ABCD是平行四边形
B、根据平行四边形的判定定理:一组对边平行且相等的四边形是平行四边形,故选项B可以判断四边形ABCD是平行四边形;
C、根据平行四边形的判定定理:两组对边分别平行的四边形是平行四边形,故选项C可以判断四边形ABCD是平行四边形;
D、根据平行四边形的判定定理:两组对边分别相等的四边形是平行四边形,故选项D可以判断四边形ABCD是平行四边形;
故选:A.
5.【解答】解:可添加AC=BD,
∵四边形ABCD的对角线互相平分,
∴四边形ABCD是平行四边形,
∵AC=BD,根据矩形判定定理对角线相等的平行四边形是矩形,
∴四边形ABCD是矩形,
故选:C.
6.【解答】解:∵∠A=90°,AC=3,AB=4,
∴BC5,
故选:D.
7.【解答】解:设BC=x,则BD=BA=x+1,
在Rt△ABC中,由勾股定理得,
AB2=AC2+BC2,
即(x+1)2=52+x2,
解得x=12,
即BC=12,
故选:C.
8.【解答】解:∵a+b=﹣6,ab=7,
∴a<0,b<0,a2+2×7+b2=36,
∴a2+b2=22,
,
故选:A.
9.【解答】解:∵∠ACB=90°,D为AB的中点,
∴CD=AD=BD,
∴∠A=∠ACD,
∵∠ACD=30°,
∴∠A=30°,
∴AB=2BC,∠ABC=60°,
∵AC2+BC2=AB2,AC=2,
∴(2)2+BC2=(2BC)2,
解得:BC=2(负数舍去),
∴AB=2BC=4,
∵AB=4,D为AB的中点,
∴BD=AD=2=BC,
∵BF⊥CD,
∴CF=DF,
∵DE∥BC,D为AB的中点,
∴AE=CE,
∴EFAD1,
故选:C.
10.【解答】解:∵,
∴,
∴
.
故选:C.
二、填空题
11.【解答】解:∵菱形ABCD的两条对角线AC、BD的长分别是8cm和6cm,
∴菱形的面积是24(cm2),
故答案为:24.
12.【解答】解:∵式子与在实数范围内有意义,
∴,解得x=2,
∴y=3,
∴xy=2×3=6.
故答案为:6.
13.【解答】解:如图:BC=12.AB=AC=10,
在△ABC中,AB=AC,AD⊥BC;
则BD=DCBC=6;
Rt△ABD中,AB=10,BD=6;
由勾股定理,得:AD8.
故答案为:8.
14.【解答】解:∵点D,E,F分别是AB,AC,BC的中点,
∴DE,EF是△ABC的中位线,
∴DE∥BC,EF∥AB,DE=BF=CFBC,EF=AD=BDAB,
∴∠ADE=∠B,∠AED=∠C,∠CEF=∠A,∠CFE=∠B,
∴△ADE≌△DBF≌△EFC(ASA),
∴S△ADE=S△DBF=S△EFC=2,DF=CE,
∴△DEF≌△BFD(SSS),
∴S△DEF=S△DBF=2,
∴四边形DBFE的面积为S△ABC﹣S△ADE﹣S△CEF=8﹣2﹣2=4,
故答案为:4.
15.【解答】解:第一种情况:把我们所看到的左面和上面组成一个平面,
则这个长方形的长和宽分别是18和6,
则所走的最短线段是AB6(cm).
第二种情况:把我们看到的前面与上面组成一个长方形,
则这个长方形的长和宽分别是14和10,
所以走的最短线段是AB2(cm).
第三种情况:把我们所看到的前面和右面组成一个长方形,
则这个长方形的长和宽分别是16和8,
所以走的最短线段是AB8(cm).
∴它需要爬行的最短路径是2cm.
故答案为:2cm.
16.【解答】解:延长BA到D,使AD=AC,连接CD,作CH⊥AB于点H,
∵3∠B+∠C=180°,∠BAC+∠B+∠C=180°,
∴∠BAC=2∠B,
∵AD=AC,
∴∠D=∠ACD,
∴∠BAC=∠D+∠ACD=2∠D,
∴∠B=∠D,
∴CB=CD,
∵CH⊥AB,
∴BH=DH,
∵AB=5,AC=CD=2,
∴BD=7,
∴,
∴,
在Rt△ACH中,,
∴,
故答案为:.
三、解答题
17.【解答】解:,
,
,
∵a﹣3≥0,3﹣a≥0,
∴a=3,
再将a=3代入得到:
,
将a=3和b=5代入原式得:.
18.【解答】解:(1)原式=(3)2﹣1﹣(12﹣41)
=27﹣1﹣12+41
=13+4;
(2)原式=2
=123﹣2
=115.
19.【解答】解:(1)△ABC是等腰三角形,理由如下:
由网格的特点和勾股定理可知,,
∴AB=BC,
∴△ABC是等腰三角形;
(2)设点B到AC的距离为h,
由网格的特点和勾股定理可知,
∵,
∴,即,
∴,
∴点B到AC的距离为.
20.【解答】解:(1)原式=(a+b)2
=20;
(2)原式=(a+b)(a﹣b)
.
21.【解答】解:(1)连接AC,
∵∠B=90°,AB=BC=2,
∴,∠BAC=45°,
∵AD=1,CD=3,
∴,CD2=9,
∴AD2+AC2=CD2,
∴△ADC是直角三角形,
∴∠DAC=90°,
∴∠DAB=∠DAC+∠BAC=135°.
(2)在 Rt△ABC中,,
在 Rt△ADC中,.
∴.
22.【解答】解:(1)在Rt△ABC中,AC=300km,BC=400km,
∴AB500(km),
答:监测点A与监测点B之间的距离为500km;
(2)海港C受台风影响,
理由:∵∠ACB=90°,CE⊥AB,
∴S△ABCAC BCCE AB,
∴300×400=500CE,
∴CE=240(km),
∵以台风中心为圆心周围260km以内为受影响区域,
∴海港C会受到此次台风的影响;
(3)以C为圆心,260km长为半径画弧,交AB于D,F,
则CD=CF=260km时,正好影响C港口,
在Rt△CDE中,
∵ED100(km),
∴DF=200km,
∵台风的速度为25千米/小时,
∴200÷25=8(小时).
答:台风影响该海港持续的时间为8小时.
23.【解答】(1)证明:由折叠的性质可知,OA=OC,EF⊥AC,
∵四边形ABCD是矩形,
∴AD∥BC,
∴∠FAO=∠ECO,
在△AOF和△COE中,
,
∴△AOF≌△COE(ASA),
∴OF=OE,
∴四边形AECF是平行四边形,
∵AC⊥EF,
∴平行四边形AECF为菱形;
(2)解:∵四边形ABCD是矩形,
∴∠B=90°,
由(1)可知,四边形AECF是菱形,
∴AE=CE=CF=AF,
设菱形AECF的边长为x,则BE=BC﹣CE=8﹣x,AE=x,
在Rt△ABE中,由勾股定理得:BE2+AB2=AE2,
即(8﹣x)2+42=x2,
解得:x=5,
即菱形AECF的边长为5.
24.【解答】解:(1)原式
=1.
原式
=10.
(2)∵,
∴,
,
∴,
1,
∵2a2+1955ab+2b2=2023,
∴2(a+b)2+1951ab=2023,
∴(a+b)2=36,
∴a>0,b>0,
∴a+b=6,
∴4m+2=6,
∴m=1;
(3)∵,
∴,
∴,
∴,
∴
=4+4×15
=64,
∵,
∴.
25.【解答】解:(1)∵四边形OABC为矩形,A(10,0),C(0,3),动点P在线段BC上以每秒2个单位长的速度由点C向B运动,点P的运动时间为t,
∴CB=OA=10,AB=OC=3,∠B=∠OAB=∠OCB=90°,CB∥OA,
∵点D是OA的中点,
∴,
由题意得:CP=2t,
∴PB=CB﹣CP=10﹣2t,
∵四边形PODB是平行四边形,
∴PB=OD=5,
∴10﹣2t=5,
∴t=2.5,
故答案为:2.5;
(2)在线段BC上存在一点Q,使得O,D,Q,P四点为顶点的四边形是菱形;理由如下:
分两种情况讨论:
①如图,当Q点在P的右边时,
∵四边形ODQP为菱形,
∴OP=PQ=OD=5,
在Rt△OPC中,由勾股定理得:,
∴2t=4,
∴t=2,
∵CQ=CP+PQ=4+5=9,
∴Q(9,3);
②如图2,当Q点在P的左边时,
∵四边形ODQP为菱形,
∴OQ=PQ=OD=5,
在Rt△OCQ中,,
∴CP=CQ+PQ=4+5=9,
∴2t=9,
∴t=4.5,
∵CQ=4,
∴Q(4,3);
综上所述,t=2秒时,Q(9,3);t=4.5秒时,Q(4,3);
(3)如图3,由(1)知:OD=5,
∵PM=5,
∴OD=PM,
∵CB∥OA,
∴四边形OPMD是平行四边形,
∴OP=DM,
∵四边形OAMP的周长为:
OA+AM+PM+OP
=10+AM+5+DM
=15+AM+DM,
∴AM+DM最小时,四边形OAMP的周长最小,
∴作点A关于BC的对称点E,连接DE交PB于M,
∴AM=EM,
∴AM+DM=DM+EM,
∵两点之间线段最短,
∴此时DM+EM最小,即AM+DM最小,
∵AE=AB+BE=3+3=6,
∴AM+DM的最小值为:,
∴四边形OAMP的周长最小值为.
21世纪教育网(www.21cnjy.com)
人教版2024—2025学年八年级下册数学期中考试全真模拟试卷
考生注意:本试卷共三道大题,25道小题,满分120分,时量120分钟
第I卷
一、选择题(每题只有一个正确选项,每小题3分,满分30分)
1.要使二次根式有意义,则x的取值范围是( )
A.x≠9 B.x>9 C.x≤9 D.x≥9
2.下列运算正确的是( )
A. B.9
C.12 D. 6
3.下列各组数中,是勾股数的为( )
A.1,1, B.1.5,2,2.5 C.4,5,6 D.5,12,13
4.下列四组条件中,不能判定四边形ABCD是平行四边形的是( )
A.AB∥DC,AD=BC B.AB∥DC,AB=DC
C.AB∥DC,AD∥BC D.AB=DC,AD=BC
5.如图,四边形ABCD的对角线互相平分,要使它变为矩形,需要添加的条件是( )
A.AB=CD B.AD=BC C.AC=BD D.AB=BC
6.已知在Rt△ABC中,∠A=90°,AC=3,AB=4,则BC的长为( )
A. B.3 C.5或 D.5
7.“今有方池一丈,葭生其中央,出水一尺,引葭赴岸,适与岸齐.问:水深几何?”这是我国数学史上的“葭生池中”问题.即AC=5,DC=1,BD=BA,则BC=( )
A.8 B.10 C.12 D.13
8.已知a+b=﹣6,ab=7.则代数式的值为( )
A. B. C. D.
9.如图,在Rt△ABC中,∠ACB=90°,D是AB的中点,且∠ACD=30°,DE∥BC交AC于点E,BF⊥CD于点F,连接EF.若AC=2,则EF的长是( )
A.2 B. C.1 D.
10.已知,则代数式的值为( )
A. B. C. D.
二、填空题(6小题,每题3分,共18分)
11.已知菱形ABCD的两条对角线AC、BD的长分别是8cm和6cm.则菱形的面积为 cm2.
12.已知,则xy= .
13.若一个等腰三角形的腰长为10,底边长为12,则其底边上的高为 .
14.如图,在△ABC中,已知点D,E,F分别是AB,AC,BC的中点,△ADE的面积为2,则四边形DBFE的面积为 .
15.如图,是一个长方体硬纸盒,现在A处有一只蚂蚁,想沿着长方体的外表面到达B处吃食物,则蚂蚁爬行的最短距离是 .
16.如图,在△ABC中,AB=5,AC=2,3∠B+∠C=180°,则S△ABC的值为 .
第II卷
人教版2024—2025学年八年级下册数学期中考试全真模拟试卷
姓名:____________ 学号:____________准考证号:___________
一、选择题
题号 1 2 3 4 5 6 7 8 9 10
答案
二、填空题
11、_______ 12、______13、_______ 14、______15、_______ 16、______
三、解答题解答题(17、18、19题每题6分,20、21每题8分,22、23每题9分,24、25每题10分,共计72分,解答题要有必要的文字说明)
17.先化简,再求值:,其中.
18.计算:
(1); (2).
19.如图,方格纸中每个小正方形的边长为1、每个小正方形的顶点称为格点.已知△ABC的三个顶点都在格点上.
(1)判断△ABC的形状,并说明理由;
(2)求点B到AC的距离.
20.已知,,求下列代数式的值.
(1)a2+b2+2ab;
(2)a2﹣b2.
21.如图,在四边形ABCD中,∠B=90°,AB=BC=2,AD=1,CD=3.
(1)求∠DAB的度数.
(2)求四边形ABCD的面积.
22.台风是一种自然灾害,它在以台风中心为圆心,一定长度为半径的圆形区域内形成极端气候,有极强的破坏力.如图,监测中心监测到一台风中心沿监测点B与监测点A所在的直线由东向西移动,已知点C为一海港,且点C与A,B两点的距离分别为300km、400km,且∠ACB=90°,过点C作CE⊥AB于点E,以台风中心为圆心,半径为260km的圆形区域内为受影响区域.
(1)求监测点A与监测点B之间的距离;
(2)请判断海港C是否会受此次台风的影响,并说明理由;
(3)若台风的速度为25km/h,则台风影响该海港多长时间
23.将矩形ABCD折叠使A,C重合,折痕交BC于E,交AD于F.
(1)求证:四边形AECF为菱形;
(2)若AB=4,BC=8,求菱形的边长.
24.阅读下列材料,然后回答问题.
学习数学,最重要的是学习数学思想,其中一种数学思想叫做换元的思想,它可以简化我们的计算,比如我们熟悉的下面这个题:已知a+b=2,ab=﹣3,求a2+b2我们可以把a+b和ab看成是一个整体,令x=a+b,y=ab,则a2+b2=(a+b)2﹣2ab=x2﹣2y=4+6=10这样,我们不用求出a,b,就可以得到最后的结果.
(1)计算: , ;
(2)m是正整数,,且2a2+1955ab+2b2=2023,求m.
(3)已知,求的值.
25.如图,O为原点,四边形OABC为矩形,已知A(10,0),C(0,3),点D是OA的中点,动点P在线段BC上以每秒2个单位长的速度由点C向B运动.设动点P的运动时间为t秒.
(1)当t= 时,四边形PODB是平行四边形;
(2)在线段BC上是否存在一点Q,使得O,D,Q,P四点为顶点的四边形是菱形?若存在,求t的值,并求出Q点的坐标;若不存在,请说明理由;
(3)在线段PB上有一点M,且PM=5,求四边形OAMP周长的最小值.
参考答案
一、选择题
题号 1 2 3 4 5 6 7 8 9 10
答案 D D D A C D C A C C
1.【解答】解:由题意得:x﹣9≥0,
解得:x≥9,
故选:D.
2.【解答】解:A、 ,故此选项错误;
B、9993,故此选项错误;
C、2,故此选项错误;
D、 6,故此选项正确;
故选:D.
3.【解答】解:A、不是正整数,不是勾股数,不符合题意;
B、1.5,2.5不是正整数,不是勾股数,不符合题意;
C、42+52≠62,不是勾股数,不符合题意;
D、因为52+122=132,所以5,12,13是勾股数,符合题意.
故选:D.
4.【解答】解:A、∵AB∥CD,AD=BC,
∴四边形ABCD可能是平行四边形,有可能是等腰梯形.
故选项A不可以判断四边形ABCD是平行四边形
B、根据平行四边形的判定定理:一组对边平行且相等的四边形是平行四边形,故选项B可以判断四边形ABCD是平行四边形;
C、根据平行四边形的判定定理:两组对边分别平行的四边形是平行四边形,故选项C可以判断四边形ABCD是平行四边形;
D、根据平行四边形的判定定理:两组对边分别相等的四边形是平行四边形,故选项D可以判断四边形ABCD是平行四边形;
故选:A.
5.【解答】解:可添加AC=BD,
∵四边形ABCD的对角线互相平分,
∴四边形ABCD是平行四边形,
∵AC=BD,根据矩形判定定理对角线相等的平行四边形是矩形,
∴四边形ABCD是矩形,
故选:C.
6.【解答】解:∵∠A=90°,AC=3,AB=4,
∴BC5,
故选:D.
7.【解答】解:设BC=x,则BD=BA=x+1,
在Rt△ABC中,由勾股定理得,
AB2=AC2+BC2,
即(x+1)2=52+x2,
解得x=12,
即BC=12,
故选:C.
8.【解答】解:∵a+b=﹣6,ab=7,
∴a<0,b<0,a2+2×7+b2=36,
∴a2+b2=22,
,
故选:A.
9.【解答】解:∵∠ACB=90°,D为AB的中点,
∴CD=AD=BD,
∴∠A=∠ACD,
∵∠ACD=30°,
∴∠A=30°,
∴AB=2BC,∠ABC=60°,
∵AC2+BC2=AB2,AC=2,
∴(2)2+BC2=(2BC)2,
解得:BC=2(负数舍去),
∴AB=2BC=4,
∵AB=4,D为AB的中点,
∴BD=AD=2=BC,
∵BF⊥CD,
∴CF=DF,
∵DE∥BC,D为AB的中点,
∴AE=CE,
∴EFAD1,
故选:C.
10.【解答】解:∵,
∴,
∴
.
故选:C.
二、填空题
11.【解答】解:∵菱形ABCD的两条对角线AC、BD的长分别是8cm和6cm,
∴菱形的面积是24(cm2),
故答案为:24.
12.【解答】解:∵式子与在实数范围内有意义,
∴,解得x=2,
∴y=3,
∴xy=2×3=6.
故答案为:6.
13.【解答】解:如图:BC=12.AB=AC=10,
在△ABC中,AB=AC,AD⊥BC;
则BD=DCBC=6;
Rt△ABD中,AB=10,BD=6;
由勾股定理,得:AD8.
故答案为:8.
14.【解答】解:∵点D,E,F分别是AB,AC,BC的中点,
∴DE,EF是△ABC的中位线,
∴DE∥BC,EF∥AB,DE=BF=CFBC,EF=AD=BDAB,
∴∠ADE=∠B,∠AED=∠C,∠CEF=∠A,∠CFE=∠B,
∴△ADE≌△DBF≌△EFC(ASA),
∴S△ADE=S△DBF=S△EFC=2,DF=CE,
∴△DEF≌△BFD(SSS),
∴S△DEF=S△DBF=2,
∴四边形DBFE的面积为S△ABC﹣S△ADE﹣S△CEF=8﹣2﹣2=4,
故答案为:4.
15.【解答】解:第一种情况:把我们所看到的左面和上面组成一个平面,
则这个长方形的长和宽分别是18和6,
则所走的最短线段是AB6(cm).
第二种情况:把我们看到的前面与上面组成一个长方形,
则这个长方形的长和宽分别是14和10,
所以走的最短线段是AB2(cm).
第三种情况:把我们所看到的前面和右面组成一个长方形,
则这个长方形的长和宽分别是16和8,
所以走的最短线段是AB8(cm).
∴它需要爬行的最短路径是2cm.
故答案为:2cm.
16.【解答】解:延长BA到D,使AD=AC,连接CD,作CH⊥AB于点H,
∵3∠B+∠C=180°,∠BAC+∠B+∠C=180°,
∴∠BAC=2∠B,
∵AD=AC,
∴∠D=∠ACD,
∴∠BAC=∠D+∠ACD=2∠D,
∴∠B=∠D,
∴CB=CD,
∵CH⊥AB,
∴BH=DH,
∵AB=5,AC=CD=2,
∴BD=7,
∴,
∴,
在Rt△ACH中,,
∴,
故答案为:.
三、解答题
17.【解答】解:,
,
,
∵a﹣3≥0,3﹣a≥0,
∴a=3,
再将a=3代入得到:
,
将a=3和b=5代入原式得:.
18.【解答】解:(1)原式=(3)2﹣1﹣(12﹣41)
=27﹣1﹣12+41
=13+4;
(2)原式=2
=123﹣2
=115.
19.【解答】解:(1)△ABC是等腰三角形,理由如下:
由网格的特点和勾股定理可知,,
∴AB=BC,
∴△ABC是等腰三角形;
(2)设点B到AC的距离为h,
由网格的特点和勾股定理可知,
∵,
∴,即,
∴,
∴点B到AC的距离为.
20.【解答】解:(1)原式=(a+b)2
=20;
(2)原式=(a+b)(a﹣b)
.
21.【解答】解:(1)连接AC,
∵∠B=90°,AB=BC=2,
∴,∠BAC=45°,
∵AD=1,CD=3,
∴,CD2=9,
∴AD2+AC2=CD2,
∴△ADC是直角三角形,
∴∠DAC=90°,
∴∠DAB=∠DAC+∠BAC=135°.
(2)在 Rt△ABC中,,
在 Rt△ADC中,.
∴.
22.【解答】解:(1)在Rt△ABC中,AC=300km,BC=400km,
∴AB500(km),
答:监测点A与监测点B之间的距离为500km;
(2)海港C受台风影响,
理由:∵∠ACB=90°,CE⊥AB,
∴S△ABCAC BCCE AB,
∴300×400=500CE,
∴CE=240(km),
∵以台风中心为圆心周围260km以内为受影响区域,
∴海港C会受到此次台风的影响;
(3)以C为圆心,260km长为半径画弧,交AB于D,F,
则CD=CF=260km时,正好影响C港口,
在Rt△CDE中,
∵ED100(km),
∴DF=200km,
∵台风的速度为25千米/小时,
∴200÷25=8(小时).
答:台风影响该海港持续的时间为8小时.
23.【解答】(1)证明:由折叠的性质可知,OA=OC,EF⊥AC,
∵四边形ABCD是矩形,
∴AD∥BC,
∴∠FAO=∠ECO,
在△AOF和△COE中,
,
∴△AOF≌△COE(ASA),
∴OF=OE,
∴四边形AECF是平行四边形,
∵AC⊥EF,
∴平行四边形AECF为菱形;
(2)解:∵四边形ABCD是矩形,
∴∠B=90°,
由(1)可知,四边形AECF是菱形,
∴AE=CE=CF=AF,
设菱形AECF的边长为x,则BE=BC﹣CE=8﹣x,AE=x,
在Rt△ABE中,由勾股定理得:BE2+AB2=AE2,
即(8﹣x)2+42=x2,
解得:x=5,
即菱形AECF的边长为5.
24.【解答】解:(1)原式
=1.
原式
=10.
(2)∵,
∴,
,
∴,
1,
∵2a2+1955ab+2b2=2023,
∴2(a+b)2+1951ab=2023,
∴(a+b)2=36,
∴a>0,b>0,
∴a+b=6,
∴4m+2=6,
∴m=1;
(3)∵,
∴,
∴,
∴,
∴
=4+4×15
=64,
∵,
∴.
25.【解答】解:(1)∵四边形OABC为矩形,A(10,0),C(0,3),动点P在线段BC上以每秒2个单位长的速度由点C向B运动,点P的运动时间为t,
∴CB=OA=10,AB=OC=3,∠B=∠OAB=∠OCB=90°,CB∥OA,
∵点D是OA的中点,
∴,
由题意得:CP=2t,
∴PB=CB﹣CP=10﹣2t,
∵四边形PODB是平行四边形,
∴PB=OD=5,
∴10﹣2t=5,
∴t=2.5,
故答案为:2.5;
(2)在线段BC上存在一点Q,使得O,D,Q,P四点为顶点的四边形是菱形;理由如下:
分两种情况讨论:
①如图,当Q点在P的右边时,
∵四边形ODQP为菱形,
∴OP=PQ=OD=5,
在Rt△OPC中,由勾股定理得:,
∴2t=4,
∴t=2,
∵CQ=CP+PQ=4+5=9,
∴Q(9,3);
②如图2,当Q点在P的左边时,
∵四边形ODQP为菱形,
∴OQ=PQ=OD=5,
在Rt△OCQ中,,
∴CP=CQ+PQ=4+5=9,
∴2t=9,
∴t=4.5,
∵CQ=4,
∴Q(4,3);
综上所述,t=2秒时,Q(9,3);t=4.5秒时,Q(4,3);
(3)如图3,由(1)知:OD=5,
∵PM=5,
∴OD=PM,
∵CB∥OA,
∴四边形OPMD是平行四边形,
∴OP=DM,
∵四边形OAMP的周长为:
OA+AM+PM+OP
=10+AM+5+DM
=15+AM+DM,
∴AM+DM最小时,四边形OAMP的周长最小,
∴作点A关于BC的对称点E,连接DE交PB于M,
∴AM=EM,
∴AM+DM=DM+EM,
∵两点之间线段最短,
∴此时DM+EM最小,即AM+DM最小,
∵AE=AB+BE=3+3=6,
∴AM+DM的最小值为:,
∴四边形OAMP的周长最小值为.
21世纪教育网(www.21cnjy.com)
同课章节目录
