2025年九年级数学中考三轮冲刺训练二次函数中几何综合问题(含答案)
文档属性
| 名称 | 2025年九年级数学中考三轮冲刺训练二次函数中几何综合问题(含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 749.5KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-03-30 00:00:00 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
2025年九年级数学中考三轮冲刺训练二次函数中几何综合问题
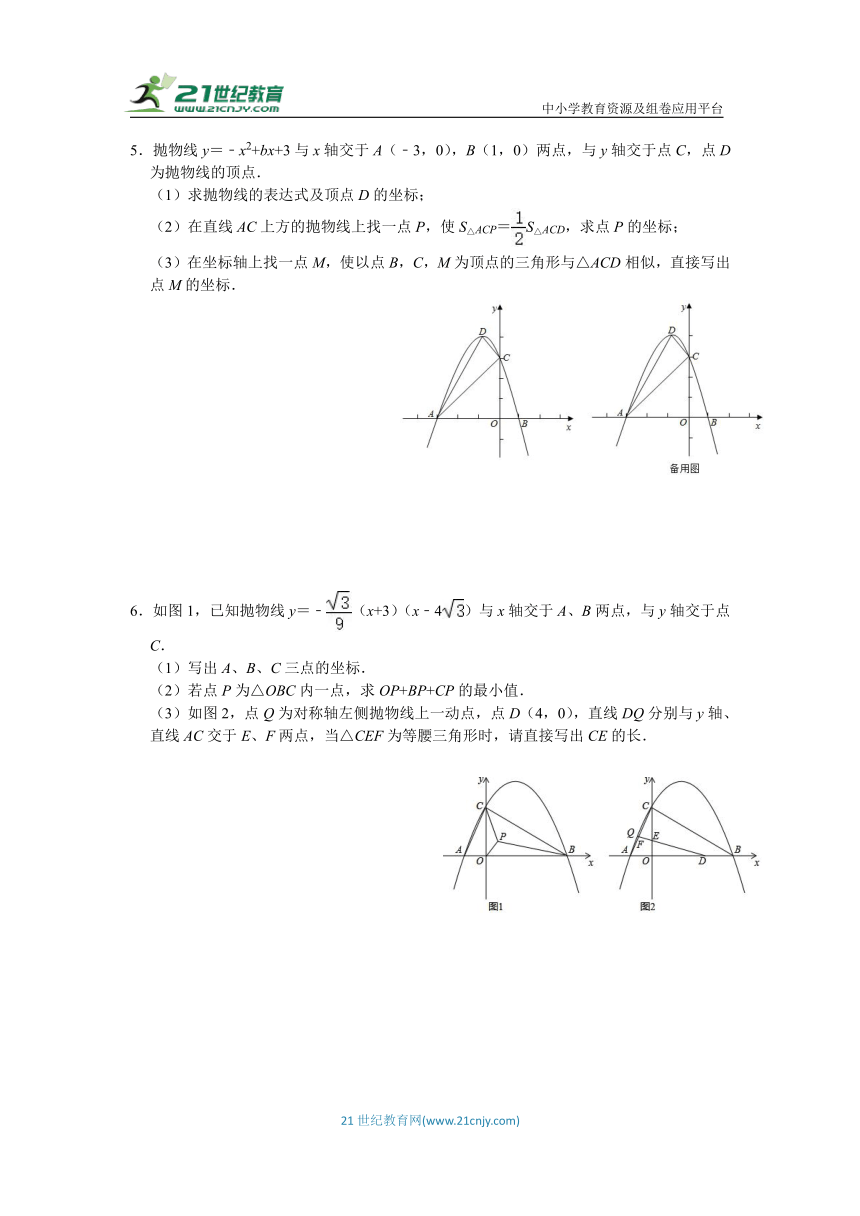
1.如图,已知二次函数y=﹣(x+1)(x﹣3m)与x轴交于点A,点B(点B在点A的右边),交y轴于点C,其中m>0.
(1)直接写出点B,点C的坐标,及抛物线的对称轴.(用m的代数式表示)
(2)过OB的中点M做x轴垂线交抛物线于点D,交BC于点N,若,求m的值.
2.如图,抛物线y=﹣x2+bx+c与x轴交于A、B两点,与y轴交于点C,其中B(1,0),C(0,3).
(1)求抛物线的解析式;
(2)在第二象限的抛物线上是否存在一点P,使得△APC的面积最大.若存在,请直接写出点P坐标和△APC的面积最大值;若不存在,请说明理由.
3.如图,拋物线y=﹣x2+bx+c的图象经过点C(0,2),交x轴于点A(﹣1,0)和B,连接BC,直线y=kx+1与y轴交于点D,与BC上方的抛物线交于点E,与BC交于点F.
(1)求抛物线的表达式及点B的坐标;
(2)求的最大值及此时点E的坐标;
(3)在(2)的条件下,若点M为直线DE上一点,点N为平面直角坐标系内一点,是否存在这样的点M和点N,使得以点B、D、M、N为顶点的四边形是菱形?若存在,直接写出点M的坐标;若不存在,请说明理由.
4.如图,抛物线y=ax2+2x+c(a<0)与x轴交于点A和点B(点A在原点的左侧,点B在原点的右侧),与y轴交于点C,OB=OC=3.
(1)求该抛物线的函数解析式;
(2)如图1,连接BC,点D是直线BC上方抛物线上的点,连接OD,CD,OD交BC于点F,当S△COF:S△CDF=3:2时,求点D的坐标.
(3)如图2,点E的坐标为(0,),在抛物线上是否存在点P,使∠OBP=2∠OBE?若存在,请直接写出符合条件的点P的坐标;若不存在,请说明理由.
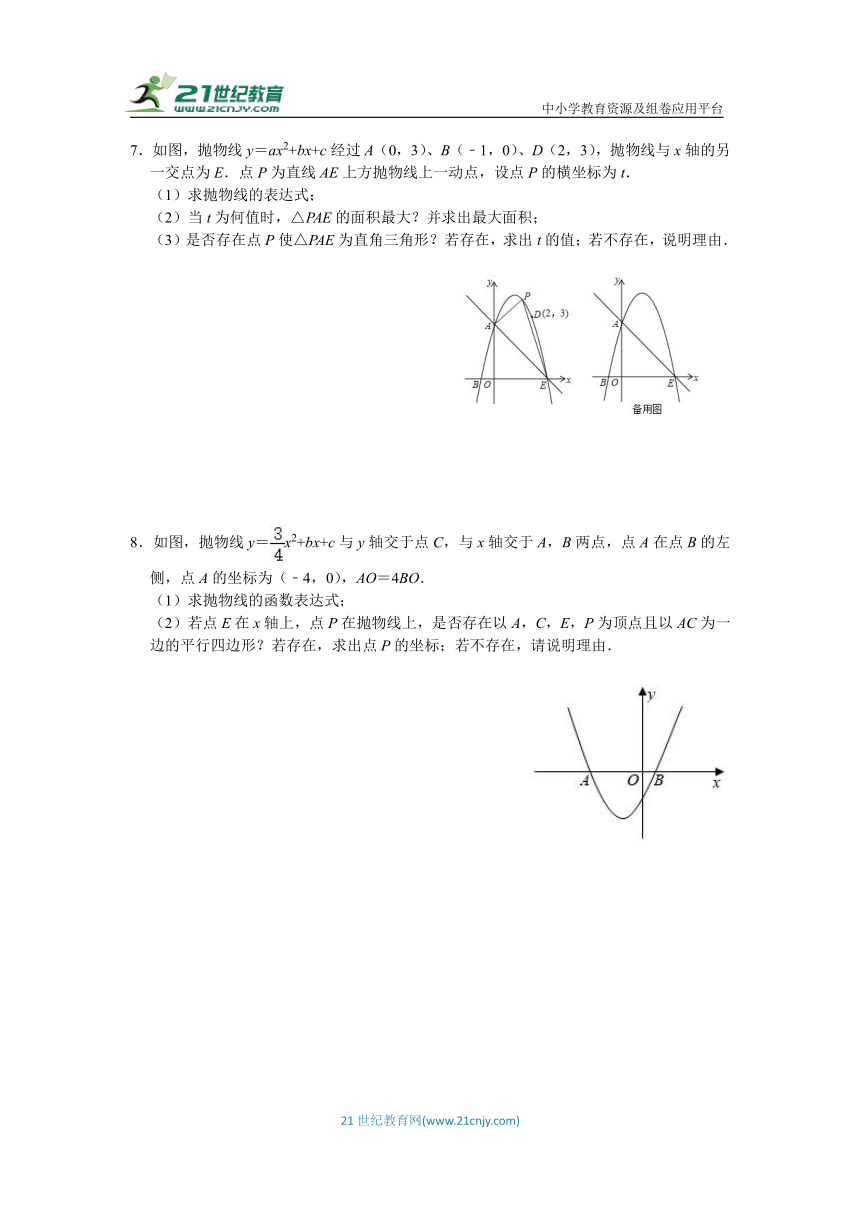
5.抛物线y=﹣x2+bx+3与x轴交于A(﹣3,0),B(1,0)两点,与y轴交于点C,点D为抛物线的顶点.
(1)求抛物线的表达式及顶点D的坐标;
(2)在直线AC上方的抛物线上找一点P,使S△ACP=S△ACD,求点P的坐标;
(3)在坐标轴上找一点M,使以点B,C,M为顶点的三角形与△ACD相似,直接写出点M的坐标.
6.如图1,已知抛物线y=﹣(x+3)(x﹣4)与x轴交于A、B两点,与y轴交于点C.
(1)写出A、B、C三点的坐标.
(2)若点P为△OBC内一点,求OP+BP+CP的最小值.
(3)如图2,点Q为对称轴左侧抛物线上一动点,点D(4,0),直线DQ分别与y轴、直线AC交于E、F两点,当△CEF为等腰三角形时,请直接写出CE的长.
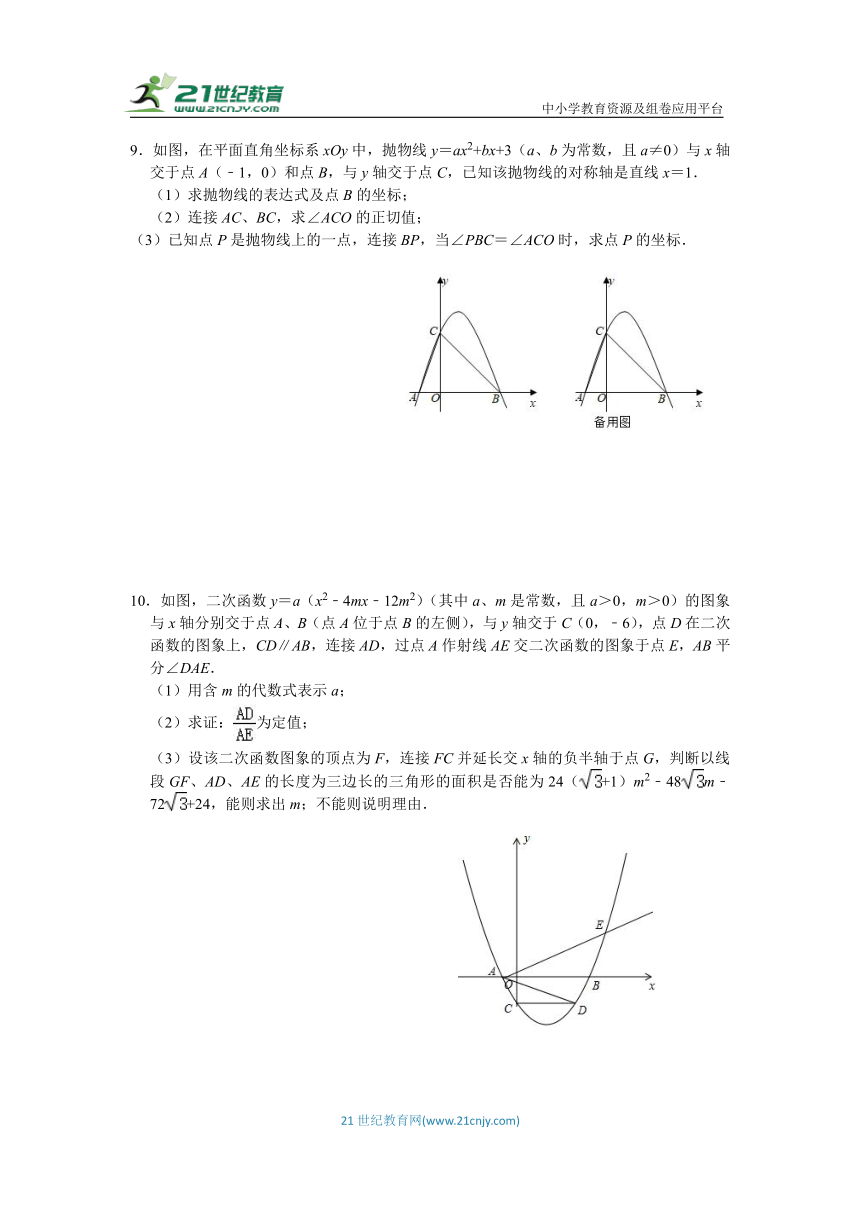
7.如图,抛物线y=ax2+bx+c经过A(0,3)、B(﹣1,0)、D(2,3),抛物线与x轴的另一交点为E.点P为直线AE上方抛物线上一动点,设点P的横坐标为t.
(1)求抛物线的表达式;
(2)当t为何值时,△PAE的面积最大?并求出最大面积;
(3)是否存在点P使△PAE为直角三角形?若存在,求出t的值;若不存在,说明理由.
8.如图,抛物线y=x2+bx+c与y轴交于点C,与x轴交于A,B两点,点A在点B的左侧,点A的坐标为(﹣4,0),AO=4BO.
(1)求抛物线的函数表达式;
(2)若点E在x轴上,点P在抛物线上,是否存在以A,C,E,P为顶点且以AC为一边的平行四边形?若存在,求出点P的坐标;若不存在,请说明理由.
9.如图,在平面直角坐标系xOy中,抛物线y=ax2+bx+3(a、b为常数,且a≠0)与x轴交于点A(﹣1,0)和点B,与y轴交于点C,已知该抛物线的对称轴是直线x=1.
(1)求抛物线的表达式及点B的坐标;
(2)连接AC、BC,求∠ACO的正切值;
(3)已知点P是抛物线上的一点,连接BP,当∠PBC=∠ACO时,求点P的坐标.
10.如图,二次函数y=a(x2﹣4mx﹣12m2)(其中a、m是常数,且a>0,m>0)的图象与x轴分别交于点A、B(点A位于点B的左侧),与y轴交于C(0,﹣6),点D在二次函数的图象上,CD∥AB,连接AD,过点A作射线AE交二次函数的图象于点E,AB平分∠DAE.
(1)用含m的代数式表示a;
(2)求证:为定值;
(3)设该二次函数图象的顶点为F,连接FC并延长交x轴的负半轴于点G,判断以线段GF、AD、AE的长度为三边长的三角形的面积是否能为24(+1)m2﹣48m﹣72+24,能则求出m;不能则说明理由.
11.如图,已知直线y=kx与抛物线y=mx2+n交于点A、C.
(1)若m=﹣1,且点A坐标为A(1,2),求抛物线解析式与点C坐标;
(2)如图1,若k=1,将直线y=x沿着x轴翻折,在第四象限交抛物线于点P,若,求mn的值;
(3)如图2,已知抛物线与直线解析式分别为y=与y=x,若点B为抛物线上对称轴右侧的点,点E在线段OA上(与点O、A不重合),点D(t,0)是x轴正半轴上的动点,记S△AEB=S1,S△EOD=S2,OE=s,OD=t,当满足∠BAE=∠BED=∠AOD的E点有两个时,求S1 S2﹣(S1+)+的最小值,并求出此时E的坐标.
12.定义:若同一函数图象上存在A(x1,y1)、B(x2,y2)、C(x3,y3)三点,满足y2﹣y1=y3﹣y2,则称ABC三点为等差点,称B为AC的等差中心.
(1)A(2,y1)、B(3,y2)、C(4,y3)是否为一次函数y=kx+2的图象上以B为等差中心的等差点?判断并说明理由;
(2)若双曲线y=上存在以B为等差中心A(x1,y1)、B(x2,y2)、C(x3,y3)的三点,其中A(x1,y1)、C(x3,y3)为反比例函数与一次函数y=nx+3的交点,若B到原点的距离为,求m的值与n的取值范围;
(3)若直线y=x与抛物线y=ax2﹣2ax+b(b>2)交于A(x1,y1)、C(x3,y3),且满足0<x2<x3<,点B(x2,y2)在直线y=x上,且为A、C的等差中心.
①证明:2<x2<
②设,当s能取得最大值时,求s的最大值的取值范围.
13.如图,在平面直角坐标系中,直线l:y=kx﹣8k(k<0)与x轴,y轴分别交于A、B两点,将直线l沿x轴翻折交y轴于点C,连接AC,过点B作BD⊥AC垂足为点D,并交x轴于点E.
(1)当∠BAO=30°时,求直线l解析式及点E坐标;
(2)若AB=2BE,求S△ABC;
(3)在(2)问条件下,构造抛物线y1,y2,其中抛物线y1经过A、B、E三点,其二次项系数为m;抛物线y2=ax2+bx+c同时满足以下三个条件:①过线段OE中点;②5a+3b+2c=0;③当≤x≤时,函数y2有最大值m;求a的值.
14.如图抛物线y=ax2+bx+c经过点A(﹣1,0),点C(0,3),且OB=OC.
(1)求抛物线的解析式及其对称轴;
(2)点D、E在直线x=1上的两个动点,且DE=1,点D在点E的上方,求四边形ACDE的周长的最小值.
(3)点P为抛物线上一点,连接CP,直线CP把四边形CBPA的面积分为3:5两部分,求点P的坐标.
15.如图,一次函数y=2x与反比例函数y=(k>0)的图象交于A、B两点,点P在以C(﹣2,0)为圆心,1为半径的圆上,Q是AP的中点
(1)若AO=,求k的值;
(2)若OQ长的最大值为,求k的值;
(3)若过点C的二次函数y=ax2+bx+c同时满足以下两个条件:①a+b+c=0;②当a≤x≤a+1时,函数y的最大值为4a,求二次项系数a的值.
16.若一个三角形一条边的平方等于另两条边的乘积,我们把这个三角形叫做比例三角形.
(1)已知△ABC是比例三角形,AB=2,BC=3,请直接写出所有满足AC条件的长;
(2)如图,点A在以BC为直径的圆上,BD平分∠ABC,AD∥BC,∠ADC=90°.
①求证:△ABC为比例三角形;
②求的值.
(3)若以点C为顶点的抛物线y=mx2﹣4mx﹣12m(m<0)与x轴交于A、B两点,△ABC是比例三角形,若点M(x0,y0)为该抛物线上任意一点,总有n﹣≤﹣my02﹣40y0+298成立,求实数n的最大值.
参考答案
1.【解答】解:(1)当y=0时,﹣(x+1)(x﹣3m)=0,解得x1=﹣1,x2=3m,
∴B点坐标为(3m,0),
当x=0时,y=﹣(x+1)(x﹣3m)=﹣1×(﹣3m)=3m,
∴C点坐标为(0,3m),
∵A(﹣1,0),B(3m,0),
∴抛物线的对称轴为直线x=﹣1=;
(2)设直线BC的解析式为y=kx+b,
把B(3m,0),C(0,3m)代入得,解得,
∴直线BC的解析式为y=﹣x+3m;
∵M点为OB的中点,
∴M(m,0),
∵DM⊥x轴,
∴N(m,m),D(m,m2+m),
∴MN=m,DN=m2+m﹣m=m2,
∵=,
∴=,
整理得m2=1,解得m1=﹣1(舍去),m2=1,
∴m的值为1.
2.【解答】解:(1)将B(1,0),C(0,3)代入抛物线y=﹣x2+bx+c中,
,
解得:,
∴抛物线y=﹣x2﹣2x+3.
(2)令y=0,则0=﹣x2﹣2x+3,
解得:x1=﹣3,x2=1,
∴A(﹣3,0),
∴OA=3,
∵C(0,3),
∴OC=3,
过点P作PE⊥x轴于点E,
设P(x,﹣x2﹣2x+3),且在第二象限内,
∴OE=﹣x,AE=3+x,
∴S△APC=S△APE+S梯形PCOE﹣S△AOC
=AE×PE(OC+PE)×OE﹣×OA×OC
=(3+x)(﹣x2﹣2x+3)+(3﹣x2﹣2x+3)(﹣x)×3×3
=(x+)2+
∵<0,
∴S有最大值,
∴当x=时,S有最大值,最大值为,
此时点P的坐标为(,).
3.【解答】解:(1)设B(xB,yB),
将A(﹣1,0),C(0,2)代入y=﹣x2+bx+c中,
得:,
解得:,
∴抛物线的表达式为:y=﹣x2+x+2,
∵点B在x轴上,
∴yB=0,
将yB=0代入y=﹣x2+x+2中,得:﹣xB2+xB+2=0,
解得:xB1=4,xB2=﹣1(不符合题意,舍去),
∴B(4,0);
(2)由题意知,点E位于y轴右侧,作EG∥y轴交BC于点G,
∴CD∥EG,
∴=,
∵直线y=kx+1与y轴交于点D,
∴D(0,1),
∴CD=2﹣1=1,
∴=EG,
设直线BC的解析式为y=mx+n(m≠0),
将B(4,0),C(0,2)代入,得:,
解得:,
∴直线BC的解析式为y=﹣x+2,
设点E(t,﹣t2+t+2),则G(t,﹣t+2),且0<t<4,
∴EG=(﹣t2+t+2)﹣(﹣t+2)=﹣t2+2t=﹣(t﹣2)2+2,
∴=﹣(t﹣2)2+2,
∵﹣<0,
∴当t=2时,的值最大,最大值为2,此时点E的坐标为(2,3);
(3)设直线DE的解析式为y=kx+b,将D(0,1),E(2,3)代入,
得:,
解得:,
∴直线DE的解析式为y=x+1,
设M(n,n+1),
∵B(4,0),D(0,1),
∴BM2=(4﹣n)2+(0﹣n﹣1)2=2n2﹣6n+17,
DM2=(0﹣n)2+(1﹣n﹣1)2=2n2,
BD2=42+12=17,
∵以点B、D、M、N为顶点的四边形是菱形,
∴分两种情况:BD为边时或BD为对角线,
①当BD为边时,MN=DM=BD(如图2)或MN=BM=BD(如图3),
∴DM2=BD2=17或BM2=BD2=17,即2n2=17或2n2﹣6n+17=17,
解得:n=±或n=0(舍去)或n=3,
∴M(,)或M(﹣,)或M(3,4),
②如图4,当BD为对角线时,设BD的中点为Q,则Q(2,),
∵四边形BMDN是菱形,
∴MN⊥BD,QB=QD=BD,
∴QD2+QM2=DM2,
∴(2﹣0)2+(﹣1)2+(n﹣2)2+(n+1﹣)2=2n2,
解得:n=,
∴M(,),
综上所述,点M的坐标为(,)或(﹣,)或(3,4)或(,).
4.【解答】解:(1)c=3,点B(3,0),
将点B的坐标代入抛物线表达式:y=ax2+2x+3并解得:a=﹣1,
故抛物线的表达式为:y=﹣x2+2x+3…①;
(2)如图1,过点D作DH⊥x轴于点H,交CB于点M,
S△COF:S△CDF=3:2,则OF:FD=3:2,
∵DH∥CO,故CO:DM=3:2,则DM=CO=2,
由B、C的坐标得:直线BC的表达式为:y=﹣x+3,
设点D(x,﹣x2+2x+3),则点M(x,﹣x+3),
DM=﹣x2+2x+3﹣(﹣x+3)=2,
解得:x=1或2,
故点D(1,4)或(2,3);
(3)①当点P在x轴上方时,
取OG=OE,连接BG,过点B作直线PB交抛物线于点P,交y轴于点M,使∠GBM=∠GBO,
则∠OBP=2∠OBE,过点G作GH⊥BM,
设MH=x,则MG=,
则△OBM中,OB2+OM2=MB2,
即(+)2+9=(x+3)2,解得:x=2,
故MG==,则点M(0,4),
将点B、M的坐标代入一次函数表达式并解得:
直线BM的表达式为:y=﹣x+4…②,
联立①②并解得:x=3(舍去)或,
故点P(,);
②当点P在x轴下方时,
同理可得:点P(﹣,﹣);
综上,点P的坐标(,)或(﹣,﹣).
5.【解答】解:(1)∵抛物线y=﹣x2+bx+3经过B(1,0),
∴﹣1+b+3=0,
解得:b=﹣2,
∴抛物线的表达式为:y=﹣x2﹣2x+3,
∵y=﹣x2﹣2x+3=﹣(x+1)2+4,
∴顶点D的坐标为(﹣1,4);
(2)在y=﹣x2﹣2x+3中,令x=0,得:y=3,
∴C(0,3),
设直线AC解析式为:y=kx+c,
∵A(﹣3,0),C(0,3),
∴,
解得:,
∴直线AC解析式为:y=x+3,
设P(m,﹣m2﹣2m+3),
过点D作DG⊥x轴交直线AC于点G,过点P作PH⊥x轴交直线AC于点H,
∴D(﹣1,4),G(﹣1,2),H(m,m+3),
∴DG=4﹣2=2,PH=﹣m2﹣2m+3﹣(m+3)=﹣m2﹣3m,
∴S△ACD= DG 3=×2=3,S△ACP= PH 3=(﹣m2﹣3m),
∵S△ACP=S△ACD,
∴(﹣m2﹣3m)=×3,
解得:m1=,m2=,
∴P1(,),P2(,);
(3)如图2,过点D作DE⊥y轴于点E,
∵A(﹣3,0),B(1,0),C(0,3),D(﹣1,4),
∴E(0,4),
∴OA=OC=3,CE=DE=1,
∵∠CED=∠AOC=90°,
∴△AOC和△CED都是等腰直角三角形,
∴∠ACO=∠DCE=45°,AC=OA=3,CD=CE=,
∴∠ACD=90°,
连接BC,在△COB中,∠BOC=90°,OB=1,OC=3,
∴=,==,
∴=,∠BOC=∠ACD,
∴△COB∽△ACD,
∴点M在O点处时符合题意,即M1(0,0),
过点C作CM2⊥BC交x轴于点M2,
∴∠BCM2=∠BOC=90°,
∴∠BCO+∠CBO=∠BCO+∠OCM2=90°,
∴∠CBO=∠OCM2,
∴△CBO∽△OCM2,
∴∠BM2C=∠BCO,
∵∠COM2=∠COB=90°,
∴△M2OC∽△COB,
∴==,
∴OM2=3OC=9,
∴M2(﹣9,0),
过点B作BM3⊥BC交y轴于点M3,
∴∠CBM3=∠COB=∠BOM3=90°,
∴∠CBO+∠BCO=∠CBO+∠OBM3=90°,
∴∠BCO=∠OBM3,
∴△BOM3∽△COB,
∴==,
∴OM3=OB=,
∴M3(0,﹣),
∵△COB∽△ACD,
∴△M2OC∽△ACD∽△BOM3,
∴点M的坐标为:(0,0)或(﹣9,0)或(0,﹣).
6.【解答】解:(1)∵y=﹣(x+3)(x﹣4)与x轴交于A、B两点,与y轴交于点C,
∴A(﹣3,0),B(4,0),C(0,4).
(2)将△BPC绕点B顺时针旋转60°得到△BP'C',连接PP',CC',
∴BP=BP',BC=BC,∠PBP'=60°,∠CBC′=60°,PC=P'C′,
∴△BPP'和△BCC′为等边三角形,
∴BC′=BC,PP′=BP,
当O,P,P',C′四点共线,OP+BP+CP的值最小,
∴tan∠OBC===,
∴∠OBC=30°,
∴BC=2OC=8,
∴BC′=BC=8,
∵∠OBC′=∠OBC+∠CBC′=30°+60°=90°,
∴OC′==,
∴OP+BP+CP=OP+PP'+C'P'=OC′=4.
(3)需要分类讨论:
①如图,当CE=CF,且点F在点C左侧时,过点F作FG⊥CE于点G,则△CFG∽△CAO,
∵OA=3,OC=4,
∴AC=5,
∴FG:GC:FC=OA:OC:AC=3:4:5,
设FG=3m,则CG=4m,FC=5m,
∴CE=FC=5m,
∴GE=m,OE=4﹣5m,
∵△FGE∽△DOE,
∴,
∴,
∴m=,
∴CE=5m=;
当点F在点C右侧时,如图所示,过点F作FG⊥y轴于点G,
则△FCG∽△ACO,
∴FG:GC:FC=OA:OC:AC=3:4:5,
设FG=3m,则CG=4m,FC=5m,
∴CE=FC=5m,
∴GE=9m,OE=5m﹣4,
∵△FGE∽△DOE,
∴,
∴,解得m=,
∴CE=5m=16;
②如图,当CE=EF时,过点A作AG∥EF交y轴于点G,由EF=CE,可得,AG=CG,
设OG=m,则AG=CG=4﹣m,
∵OA2+OG2=AG2,
∴32+m2=(4﹣m)2,解得,m=.
由A(﹣3,0)和G(0,),可得直线AG的解析式为:y=x+,
设直线DF为:y=x+b,将D(4,0)代入得:b=﹣,
∴E(0,﹣),
∴CE=4+=.
③如图,当CF=EF时,过点C作CG∥DE交x轴于点G,则∠GCO=∠ACO,
∴OG=OA=3,
∴G(3,0),
由G(3,0),C(0,4)可得直线CG的解析式为:y=﹣x+4,
设直线DE为:y=﹣x+n,将D(4,0)代入得:n=,
∴E(0,),
∴CE=﹣4=.
故CE的长为:或或或16.
7.【解答】解:(1)由题意得:,
解得:,
∴抛物线解析式为y=﹣x2+2x+3;
(2)∵A(0,3),D(2,3),
∴抛物线对称轴为x=1,
∴E(3,0),
设直线AE的解析式为y=kx+3,
∴3k+3=0,解得,k=﹣1,
∴直线AE的解析式为y=﹣x+3,
如图1,作PM∥y轴,交直线AE于点M,设P(t,﹣t2+2t+3),M(t,﹣t+3),
∴PM=﹣t2+2t+3+t﹣3=﹣t2+3t,
∴==,
∴t=时,△PAE的面积最大,最大值是.
(3)由图可知∠PEA≠90°,
∴只能有∠PAE=90°或∠APE=90°,
①当∠PAE=90°时,如图2,作PG⊥y轴,
∵OA=OE,
∴∠OAE=∠OEA=45°,
∴∠PAG=∠APG=45°,
∴PG=AG,
∴t=﹣t2+2t+3﹣3,即﹣t2+t=0,解得t=1或t=0(舍去),
②当∠APE=90°时,如图3,作PK⊥x轴,AQ⊥PK,
则PK=﹣t2+2t+3,AQ=t,KE=3﹣t,PQ=﹣t2+2t+3﹣3=﹣t2+2t,
∵∠APQ+∠KPE=∠APQ+∠PAQ=90°,
∴∠PAQ=∠KPE,且∠PKE=∠PQA,
∴△PKE∽△AQP,
∴,
∴,
即t2﹣t﹣1=0,解得:t=或t=<0(舍去),
综上可知存在满足条件的点P,t的值为1或.
8.【解答】解:(1)∵A(﹣4,0),且AO=4BO,
∴OB=OA=1,
∴B(1,0).
把A(﹣4,0)、B(1,0)代入y=x2+bx+c,
得,解得,
∴抛物线的函数表达式为y=x2+x﹣3;
(2)存在.
由抛物线y=x2+x﹣3与y轴交于点C,得C(0,﹣3);
∵以A,C,E,P为顶点的平行四边形以AC为一边,
∴点P到x轴的距离与点C到x轴的距离相等.
如图1,点P在x轴的下方,
则x2+x﹣3=﹣3,
解得x1=﹣3,x2=0(不符合题意,舍去),
∴点P的坐标为(﹣3,﹣3),
如图2,点P在x轴的上方,
则x2+x﹣3=3,
解得x1=,x2=.
∴点P的坐标为(,3)或(,0).
综上所述,点P的坐标为(﹣3,﹣3)或(,3)或(,0).
9.【解答】解:(1)∵抛物线y=ax2+bx+3与x轴交于点A(﹣1,0)且抛物线的对称轴是直线x=1,
∴,
解得:,
∴抛物线的表达式为:y=﹣x2+2x+3;
令y=0,则﹣x2+2x+3=0,
解得:x1=﹣1,x2=3,
∴B(3,0),
(2)令抛物线y=﹣x2+2x+3中,x=0,则y=3,
即,C(0,3),在Rt△AOC中,AO=1,CO=3,
因此,tan∠ACO==,
(3)如图所示,过点C作MN⊥BC交BP于M、N点,即点P分别位于线段BC的上方或下方,
①当P位于线段BC的上方,过N作y轴垂线交于E点,
∵0C=BC=3,
∴BC=3,
∴△COB为等腰直角三角形,
而MN⊥BC,
∴△COB∽△NEC,
故△NEC也为等腰直角三角形,
∵tan∠ACO=tan∠NBC==,
∴NC=,
∴NE=EC=1,
故N(1,4),而(1,4)刚好为抛物线顶点坐标,即N与P重合,
∴P(1,4),
②当P位于线段BC的下方,过M作y轴垂线交于F点,
∵tan∠ACO=tan∠MBC==,
∴MC=,
而EN∥MF,
∴∠CMF=45°,即△CMF也为等腰直角三角形,
∵MF=CF=1,
∴M(﹣1,2),
而点P'在直线MB上且与抛物线相交,
∴设直线MB的解析式为y=kx+b,将B、M坐标代入得:
,
解得:,
∴直线MB的解析式为:y=﹣x+,
联立方程:,
解得:或(舍去),
故P'(﹣,),
综上所述,当∠PBC=∠ACO时,点P的坐标为(1,4)或(﹣,).
10.【解答】解:(1)将C(0,﹣6)代入二次函数y=a(x2﹣4mx﹣12m2),
则﹣6=a(0﹣0﹣12m2),
解得a=;
(2)证明:如图1,过点D、E分别作x轴的垂线,垂足为M、N.
由a(x2﹣4mx﹣12m2)=0,
解得x1=﹣2m,x2=6m,
则点A(﹣2m,0),B(6m,0),
∵CD∥AB,
∴点D的坐标为(4m,﹣6),
∵AB平分∠DAE,
∴∠DAM=∠EAN,
∴∠DMA=∠ENA=90°,
∴△ADM∽△AEN,
∴==,
设点E坐标为(x,( x2﹣4mx﹣12m2)),
∴=,
∴x=8m,
∴E(8m,10),
∵AM=AO+OM=2m+4m=6m,AN=AO+ON=2m+8m=10m,
∴==,即为定值.
(3)如图2,记二次函数图象的顶点为F,则F的坐标为(2m,﹣8),过点F作FH⊥x轴于点H,
∵tan∠CGO=,tan∠FGH=,
∴=,即=,
∴OG=6m,
∵GF==8,AD==6,
∴=,
∵=,
∴AD:GF:AE=3:4:5,
∴以线段GF,AD,AE的长度为三边长的三角形是直角三角形,
∴以线段GF,AD,AE的长度为三边长的三角形的面积为GF AD=24(m2+1),
∴24(+1)m2﹣48m﹣72+24=24(m2+1),
∴m=3或m=﹣1,
∵m>0,
∴m=3.
11.【解答】解:(1)∵点A(1,2)在直线y=kx上
∴k=2,即直线为y=2x
∵点A(1,2)在抛物线y=mx2+n上,m=﹣1
∴﹣1+n=2,解得:n=3
∴抛物线解析式为y=﹣x2+3
解得:(即点A)
∴点C坐标为(﹣3,﹣6);
(2)过点A作AM⊥x轴于点M,过点P作PN⊥x轴于点N
∴∠OMA=∠ONP=90°
∵点A在直线y=x上,设A(a,a)(a>0)
∴OM=AM=a,∠AOM=45°
∵点A关于x轴对称点A'(a,﹣a)
∴直线y=x沿着x轴翻折得到直线OA'解析式为y=﹣x,∠PON=∠AOM=45°
∴△AOM、△PON都是等腰直角三角形
∵
∴
∴ON=PN=2a
∴P(2a,﹣2a)
∵点A、P都在抛物线y=mx2+n
∴
①﹣②消去n后整理得:ma=﹣1,即a=﹣
①×4﹣②消去ma2后整理得:n=2a
∴n=﹣
∴mn=﹣2;
(3)过点E作EH⊥x轴于点H
解得:,,
∵点A在第一象限
∴A(1,),OA=,tan∠AOD=
∴∠AOD=60°
∴∠BAE=∠BED=∠AOD=60°
设直线AB与x轴交点为F,则△AOF为等边三角形
∴OF=OA=2,F(2,0)
设直线AB解析式为:y=kx+b
解得:
∴直线AB:y=﹣x+2
解得:(即点A)
∴点B与点F重合,点B在x轴上
∴OB=AB=OA=2
∵∠BAE=∠BED,∠BEO=∠BAE+∠ABE=∠BED+∠OED
∴∠ABE=∠OED
∵∠BAE=∠AOD
∴△ABE∽△OED
∴ 即
∴t==﹣(s﹣1)2+,故0<t<;
∵OE=s,sin∠EOH==
∴EH=OE=s
∴S2=S△EOD=OD EH=st==
∵
∴S1==
∴S1 S2﹣(S1+)+=﹣[+]+=,
令s(2﹣s)=u,则原式=u2﹣u+=,
∵>0,
∴当u=时,S1 S2﹣(S1+)+的最小值为,
此时,s(2﹣s)=,解得:s1=,s2=,
当s=或时,均满足0<t<;
∴当OE=s1=时,OH=cos60°=,EH=sin60°=,
∴E1(,)
当OE=s2=时,OH=cos60°=,EH=sin60°=,
∴E2(,),
综上所述,E的坐标为:E1(,),E2(,).
12.【解答】解:(1)A(2,y1),B(3,y2),C(4,y3)为一次函数y=kx+2的图象上以B为等差中心的等差点,理由如下:
∵点A(2,y1),B(3,y2),C(4,y3)为一次函数y=kx+2的图象上的点,
∴y1=2k+2,y2=3k+2,y3=3k+2.
∵y2﹣y1=k=y3﹣y2,
∴A(2,y1),B(3,y2),C(4,y3)为一次函数y=kx+2的图象上以B为等差中心的等差点.
(2)y1=,y2=,y3=,
∴y2﹣y1=﹣=|m|,y3﹣y2=﹣=|m|,
∴|m|=|m|,
∴=2,
∵A(x1,y1)、C(x3,y3)为反比例函数与一次函数y=nx+3的交点,
∴,
∴nx2+3x﹣|m|=0,
∴x1+x3=﹣,x1x3=﹣,△=9+4n|m|>0,
又因为=2,
∵2y2=y1+y3,
∴2y2=n(x1+x3)+6,
∴2=n(x1+x3)+6=﹣3+6=3,
∴x2=,
∴y3=,
∴x2=,
∴y2=,
∵B到原点的距离为,
∴m2+=3,
∴m=±,
∴△=9+4n|m|=9+3n>0,
∴n>﹣,
∴n的取值范围n>﹣且n≠0;
(3)①直线y=x与抛物线y=ax2﹣2ax+b(b>2)交于A(x1,y1)、C(x3,y3),
∴ax2﹣2ax+b=x,
ax2﹣2ax﹣x+b=0,
∴x1+x3=,
又∵点B(x2,y2)在直线y=x上,且为A、C的等差中心.
∴2y2=2x2=,
∴x2=,
∵0<x2<x3<,
∴<,
∴0<a<,
∴x2==1+>2,
∴2<x2<.
②=﹣x22+6b+2015=﹣x22+12ax2+2015=﹣(x2﹣6a)2+2015+36a2,
∴s能取得最大值,
∴s的最大值为2015+36a2,
∵0<a<,
∴2015<2015+36a2<2024,
∴s的最大值的取值范围是2015<2015+36a2<2024.
13.【解答】解:(1)∵y=kx﹣8k(k<0)与x轴,y轴分别交于A、B两点,
∴点A(8,0),点B(0,﹣8k)
∵∠BAO=30°
∴tan∠BAO==
即=
∴k=﹣
即点B(0,),BO=
∴直线解析式y=﹣x+
∵将直线l沿x轴翻折交y轴于点C
∴AC=AB,∠BAO=∠CAO=30°
∴∠BAC=60°
∴△ABC是等边三角形,且BD⊥AC
∴∠CBD=30°=∠ABD
∴BO=OE
∴OE=
∴点E(,0)
(2)∵翻折
∴∠BAO=∠CAO,OB=OC
∵AO⊥BO,BD⊥AC
∴∠OBE+∠BEO=90°,∠CAO+∠AED=90°
∴∠OBE=∠CAO=∠BAO
且∠AOB=∠AOB
∴△BOE∽△AOB
∴,且AB=2BE
∴
∴OB=4=OC
∴BC=OB+OC=8
∴S△ABC=×8×8=32
(3)∵△BOE∽△AOB
∴
∴OE=2,OB=4
∴点A(8,0),点B(0,4),点E(2,0)
∵抛物线y1经过A、B、E三点,其二次项系数为m;
∴设y1=m(x﹣2)(x﹣8)过点B
∴4=16m
∴m=
∵点O(0,0),点E(2,0)
∴线段OE的中点(1,0)
∵抛物线y2=ax2+bx+c过线段OE中点;且5a+3b+2c=0;
∴
解得:
∴抛物线y2=ax2+bx+c=ax2﹣3ax+2a=a(x﹣1)(x﹣2)
∴对称轴为直线x=
∵当≤x≤时,函数y2有最大值m;
∴当≤x≤2时,函数y2有最大值;
若a>0时,当x=时,函数y2有最大值.
∴a(﹣1)(﹣2)=
∴a=
若a<0时,当x=,函数y2有最大值.
∴a(﹣1)(﹣2)=
∴a=﹣1
综上所述:a=﹣或﹣1
14.【解答】解:(1)∵OB=OC,∴点B(3,0),
则抛物线的表达式为:y=a(x+1)(x﹣3)=a(x2﹣2x﹣3)=ax2﹣2ax﹣3a,
故﹣3a=3,解得:a=﹣1,
故抛物线的表达式为:y=﹣x2+2x+3…①,
函数的对称轴为:x=1;
(2)四边形ACDE的周长=AC+DE+CD+AE,其中AC=、DE=1是常数,
故CD+AE最小时,周长最小,
取点C关于函数对称点C′(2,3),则CD=C′D,
取点A′(﹣1,1),则A′D=AE,
故:CD+AE=A′D+DC′,则当A′、D、C′三点共线时,CD+AE=A′D+DC′最小,周长也最小,
四边形ACDE的周长的最小值=AC+DE+CD+AE=+A′D+DC′=+A′C′=+;
(3)如图,设直线CP交x轴于点E,
直线CP把四边形CBPA的面积分为3:5两部分,
又∵S△PCB:S△PCA=EB×(yC﹣yP):AE×(yC﹣yP)=BE:AE,
则BE:AE=3:5或5:3,
则AE=或,
即:点E的坐标为(,0)或(,0),
将点E的坐标代入直线CP的表达式:y=kx+3,
解得:k=﹣6或﹣2,
故直线CP的表达式为:y=﹣2x+3或y=﹣6x+3…②
联立①②并解得:x=4或8(不合题意值已舍去),
故点P的坐标为(4,﹣5)或(8,﹣45).
15.【解答】解:(1)设A(m,n),
∵AO=,
∴m2+n2=5,
∵一次函数y=2x的图象经过A点,
∴n=2m,
∴m2+(2m)2=5,解得m=±1,
∵A在第一象限,
∴m=1,
∴A(1,2),
∵点A在反比例函数y=(k>0)的图象上,
∴k=1×2=2;
(2)连接BP,
由对称性得:OA=OB,
∵Q是AP的中点,
∴OQ=BP,
∵OQ长的最大值为,
∴BP长的最大值为×2=3,
如图2,当BP过圆心C时,BP最长,过B作BD⊥x轴于D,
∵CP=1,
∴BC=2,
∵B在直线y=2x上,
设B(t,2t),则CD=t﹣(﹣2)=t+2,BD=﹣2t,
在Rt△BCD中,由勾股定理得:BC2=CD2+BD2,
∴22=(t+2)2+(﹣2t)2,
t=0(舍)或﹣,
∴B(﹣,﹣),
∵点B在反比例函数y=(k>0)的图象上,
∴k=﹣×(﹣)=;
(3)∵抛物线经过点C(﹣2,0),
∴4a﹣2b+c=0,
又∵a+b+c=0,
∴b=a,c=﹣2a,
∴y=ax2+ax﹣2a=a(x+)2﹣a,
∵﹣<a≤x≤a+1或a≤x≤a+1<﹣,
∴当x=a时,取得最大值4a,
则a a2+a a﹣2a=4a,
解得a=﹣3或2(不合题意舍去),
当x=a+1时,取得最大值4a,
则a(a+1)2+a(a+1)﹣2a=4a,
解得a=1或﹣4,
综上所述所求a的值为﹣4或1.
16.【解答】解:(1)∵AB=2,BC=3
∴1<AC<5
①若AB2=BC AC,则AC=
②若BC2=AB AC,则AC=
③若AC2=AB BC=6,则AC=
综上所述,满足条件的AC的长为,,.
(2)①证明:∵AD∥BC
∴∠DAC=∠ACB,∠ADB=∠DBC
∵BD平分∠ABC
∴∠ABD=∠DBC
∴∠ABD=∠ADB
∴AB=AD
∵点A在以BC为直径的圆上
∴∠BAC=90°
∵∠BAC=∠CDA=90°,∠ACB=∠DAC
∴△ABC∽△DCA
∴
∴AC2=BC DA=BC AB
∴△ABC为比例三角形
②∵∠BAC=∠CDA=90°,AB=AD
∴BC2=AB2+AC2,AC2=AD2+CD2=AB2+CD2
∵AD∥BC
∴∠BCD=180°﹣∠ADC=90°
∴BD2=BC2+CD2=AB2+AC2+AC2﹣AB2=2AC2
∴BD=AC
∴
(3)∵y=mx2﹣4mx﹣12m=m(x﹣2)2﹣16m(m<0)
∴抛物线开口向下,顶点C(2,﹣16m)
∵y=0时,mx2﹣4mx﹣12m=0
解得:x1=﹣2,x2=6
∴A(﹣2,0),B(6,0),AB=8
∴AC=BC=
∵△ABC是比例三角形
∴AB2=BC AC或AC2=AB BC
∴AB=AC
∴4=8
解得:m1=(舍去),m2=﹣
∴抛物线解析式为y=﹣x2+x+3=﹣(x﹣2)2+4
∵M(x0,y0)在抛物线上
∴y0≤4
设z=﹣my02﹣40y0+298=4y02﹣40y0+298=4(y0﹣5)2﹣2
∴当y0≤4时,z随x的增大而减小
∴y0=4时,z最小值=4×(4﹣5)2﹣2=4×3﹣2=10
∵n﹣≤z恒成立,即n﹣≤10
∴n的最大值为10+
21世纪教育网(www.21cnjy.com)
2025年九年级数学中考三轮冲刺训练二次函数中几何综合问题
1.如图,已知二次函数y=﹣(x+1)(x﹣3m)与x轴交于点A,点B(点B在点A的右边),交y轴于点C,其中m>0.
(1)直接写出点B,点C的坐标,及抛物线的对称轴.(用m的代数式表示)
(2)过OB的中点M做x轴垂线交抛物线于点D,交BC于点N,若,求m的值.
2.如图,抛物线y=﹣x2+bx+c与x轴交于A、B两点,与y轴交于点C,其中B(1,0),C(0,3).
(1)求抛物线的解析式;
(2)在第二象限的抛物线上是否存在一点P,使得△APC的面积最大.若存在,请直接写出点P坐标和△APC的面积最大值;若不存在,请说明理由.
3.如图,拋物线y=﹣x2+bx+c的图象经过点C(0,2),交x轴于点A(﹣1,0)和B,连接BC,直线y=kx+1与y轴交于点D,与BC上方的抛物线交于点E,与BC交于点F.
(1)求抛物线的表达式及点B的坐标;
(2)求的最大值及此时点E的坐标;
(3)在(2)的条件下,若点M为直线DE上一点,点N为平面直角坐标系内一点,是否存在这样的点M和点N,使得以点B、D、M、N为顶点的四边形是菱形?若存在,直接写出点M的坐标;若不存在,请说明理由.
4.如图,抛物线y=ax2+2x+c(a<0)与x轴交于点A和点B(点A在原点的左侧,点B在原点的右侧),与y轴交于点C,OB=OC=3.
(1)求该抛物线的函数解析式;
(2)如图1,连接BC,点D是直线BC上方抛物线上的点,连接OD,CD,OD交BC于点F,当S△COF:S△CDF=3:2时,求点D的坐标.
(3)如图2,点E的坐标为(0,),在抛物线上是否存在点P,使∠OBP=2∠OBE?若存在,请直接写出符合条件的点P的坐标;若不存在,请说明理由.
5.抛物线y=﹣x2+bx+3与x轴交于A(﹣3,0),B(1,0)两点,与y轴交于点C,点D为抛物线的顶点.
(1)求抛物线的表达式及顶点D的坐标;
(2)在直线AC上方的抛物线上找一点P,使S△ACP=S△ACD,求点P的坐标;
(3)在坐标轴上找一点M,使以点B,C,M为顶点的三角形与△ACD相似,直接写出点M的坐标.
6.如图1,已知抛物线y=﹣(x+3)(x﹣4)与x轴交于A、B两点,与y轴交于点C.
(1)写出A、B、C三点的坐标.
(2)若点P为△OBC内一点,求OP+BP+CP的最小值.
(3)如图2,点Q为对称轴左侧抛物线上一动点,点D(4,0),直线DQ分别与y轴、直线AC交于E、F两点,当△CEF为等腰三角形时,请直接写出CE的长.
7.如图,抛物线y=ax2+bx+c经过A(0,3)、B(﹣1,0)、D(2,3),抛物线与x轴的另一交点为E.点P为直线AE上方抛物线上一动点,设点P的横坐标为t.
(1)求抛物线的表达式;
(2)当t为何值时,△PAE的面积最大?并求出最大面积;
(3)是否存在点P使△PAE为直角三角形?若存在,求出t的值;若不存在,说明理由.
8.如图,抛物线y=x2+bx+c与y轴交于点C,与x轴交于A,B两点,点A在点B的左侧,点A的坐标为(﹣4,0),AO=4BO.
(1)求抛物线的函数表达式;
(2)若点E在x轴上,点P在抛物线上,是否存在以A,C,E,P为顶点且以AC为一边的平行四边形?若存在,求出点P的坐标;若不存在,请说明理由.
9.如图,在平面直角坐标系xOy中,抛物线y=ax2+bx+3(a、b为常数,且a≠0)与x轴交于点A(﹣1,0)和点B,与y轴交于点C,已知该抛物线的对称轴是直线x=1.
(1)求抛物线的表达式及点B的坐标;
(2)连接AC、BC,求∠ACO的正切值;
(3)已知点P是抛物线上的一点,连接BP,当∠PBC=∠ACO时,求点P的坐标.
10.如图,二次函数y=a(x2﹣4mx﹣12m2)(其中a、m是常数,且a>0,m>0)的图象与x轴分别交于点A、B(点A位于点B的左侧),与y轴交于C(0,﹣6),点D在二次函数的图象上,CD∥AB,连接AD,过点A作射线AE交二次函数的图象于点E,AB平分∠DAE.
(1)用含m的代数式表示a;
(2)求证:为定值;
(3)设该二次函数图象的顶点为F,连接FC并延长交x轴的负半轴于点G,判断以线段GF、AD、AE的长度为三边长的三角形的面积是否能为24(+1)m2﹣48m﹣72+24,能则求出m;不能则说明理由.
11.如图,已知直线y=kx与抛物线y=mx2+n交于点A、C.
(1)若m=﹣1,且点A坐标为A(1,2),求抛物线解析式与点C坐标;
(2)如图1,若k=1,将直线y=x沿着x轴翻折,在第四象限交抛物线于点P,若,求mn的值;
(3)如图2,已知抛物线与直线解析式分别为y=与y=x,若点B为抛物线上对称轴右侧的点,点E在线段OA上(与点O、A不重合),点D(t,0)是x轴正半轴上的动点,记S△AEB=S1,S△EOD=S2,OE=s,OD=t,当满足∠BAE=∠BED=∠AOD的E点有两个时,求S1 S2﹣(S1+)+的最小值,并求出此时E的坐标.
12.定义:若同一函数图象上存在A(x1,y1)、B(x2,y2)、C(x3,y3)三点,满足y2﹣y1=y3﹣y2,则称ABC三点为等差点,称B为AC的等差中心.
(1)A(2,y1)、B(3,y2)、C(4,y3)是否为一次函数y=kx+2的图象上以B为等差中心的等差点?判断并说明理由;
(2)若双曲线y=上存在以B为等差中心A(x1,y1)、B(x2,y2)、C(x3,y3)的三点,其中A(x1,y1)、C(x3,y3)为反比例函数与一次函数y=nx+3的交点,若B到原点的距离为,求m的值与n的取值范围;
(3)若直线y=x与抛物线y=ax2﹣2ax+b(b>2)交于A(x1,y1)、C(x3,y3),且满足0<x2<x3<,点B(x2,y2)在直线y=x上,且为A、C的等差中心.
①证明:2<x2<
②设,当s能取得最大值时,求s的最大值的取值范围.
13.如图,在平面直角坐标系中,直线l:y=kx﹣8k(k<0)与x轴,y轴分别交于A、B两点,将直线l沿x轴翻折交y轴于点C,连接AC,过点B作BD⊥AC垂足为点D,并交x轴于点E.
(1)当∠BAO=30°时,求直线l解析式及点E坐标;
(2)若AB=2BE,求S△ABC;
(3)在(2)问条件下,构造抛物线y1,y2,其中抛物线y1经过A、B、E三点,其二次项系数为m;抛物线y2=ax2+bx+c同时满足以下三个条件:①过线段OE中点;②5a+3b+2c=0;③当≤x≤时,函数y2有最大值m;求a的值.
14.如图抛物线y=ax2+bx+c经过点A(﹣1,0),点C(0,3),且OB=OC.
(1)求抛物线的解析式及其对称轴;
(2)点D、E在直线x=1上的两个动点,且DE=1,点D在点E的上方,求四边形ACDE的周长的最小值.
(3)点P为抛物线上一点,连接CP,直线CP把四边形CBPA的面积分为3:5两部分,求点P的坐标.
15.如图,一次函数y=2x与反比例函数y=(k>0)的图象交于A、B两点,点P在以C(﹣2,0)为圆心,1为半径的圆上,Q是AP的中点
(1)若AO=,求k的值;
(2)若OQ长的最大值为,求k的值;
(3)若过点C的二次函数y=ax2+bx+c同时满足以下两个条件:①a+b+c=0;②当a≤x≤a+1时,函数y的最大值为4a,求二次项系数a的值.
16.若一个三角形一条边的平方等于另两条边的乘积,我们把这个三角形叫做比例三角形.
(1)已知△ABC是比例三角形,AB=2,BC=3,请直接写出所有满足AC条件的长;
(2)如图,点A在以BC为直径的圆上,BD平分∠ABC,AD∥BC,∠ADC=90°.
①求证:△ABC为比例三角形;
②求的值.
(3)若以点C为顶点的抛物线y=mx2﹣4mx﹣12m(m<0)与x轴交于A、B两点,△ABC是比例三角形,若点M(x0,y0)为该抛物线上任意一点,总有n﹣≤﹣my02﹣40y0+298成立,求实数n的最大值.
参考答案
1.【解答】解:(1)当y=0时,﹣(x+1)(x﹣3m)=0,解得x1=﹣1,x2=3m,
∴B点坐标为(3m,0),
当x=0时,y=﹣(x+1)(x﹣3m)=﹣1×(﹣3m)=3m,
∴C点坐标为(0,3m),
∵A(﹣1,0),B(3m,0),
∴抛物线的对称轴为直线x=﹣1=;
(2)设直线BC的解析式为y=kx+b,
把B(3m,0),C(0,3m)代入得,解得,
∴直线BC的解析式为y=﹣x+3m;
∵M点为OB的中点,
∴M(m,0),
∵DM⊥x轴,
∴N(m,m),D(m,m2+m),
∴MN=m,DN=m2+m﹣m=m2,
∵=,
∴=,
整理得m2=1,解得m1=﹣1(舍去),m2=1,
∴m的值为1.
2.【解答】解:(1)将B(1,0),C(0,3)代入抛物线y=﹣x2+bx+c中,
,
解得:,
∴抛物线y=﹣x2﹣2x+3.
(2)令y=0,则0=﹣x2﹣2x+3,
解得:x1=﹣3,x2=1,
∴A(﹣3,0),
∴OA=3,
∵C(0,3),
∴OC=3,
过点P作PE⊥x轴于点E,
设P(x,﹣x2﹣2x+3),且在第二象限内,
∴OE=﹣x,AE=3+x,
∴S△APC=S△APE+S梯形PCOE﹣S△AOC
=AE×PE(OC+PE)×OE﹣×OA×OC
=(3+x)(﹣x2﹣2x+3)+(3﹣x2﹣2x+3)(﹣x)×3×3
=(x+)2+
∵<0,
∴S有最大值,
∴当x=时,S有最大值,最大值为,
此时点P的坐标为(,).
3.【解答】解:(1)设B(xB,yB),
将A(﹣1,0),C(0,2)代入y=﹣x2+bx+c中,
得:,
解得:,
∴抛物线的表达式为:y=﹣x2+x+2,
∵点B在x轴上,
∴yB=0,
将yB=0代入y=﹣x2+x+2中,得:﹣xB2+xB+2=0,
解得:xB1=4,xB2=﹣1(不符合题意,舍去),
∴B(4,0);
(2)由题意知,点E位于y轴右侧,作EG∥y轴交BC于点G,
∴CD∥EG,
∴=,
∵直线y=kx+1与y轴交于点D,
∴D(0,1),
∴CD=2﹣1=1,
∴=EG,
设直线BC的解析式为y=mx+n(m≠0),
将B(4,0),C(0,2)代入,得:,
解得:,
∴直线BC的解析式为y=﹣x+2,
设点E(t,﹣t2+t+2),则G(t,﹣t+2),且0<t<4,
∴EG=(﹣t2+t+2)﹣(﹣t+2)=﹣t2+2t=﹣(t﹣2)2+2,
∴=﹣(t﹣2)2+2,
∵﹣<0,
∴当t=2时,的值最大,最大值为2,此时点E的坐标为(2,3);
(3)设直线DE的解析式为y=kx+b,将D(0,1),E(2,3)代入,
得:,
解得:,
∴直线DE的解析式为y=x+1,
设M(n,n+1),
∵B(4,0),D(0,1),
∴BM2=(4﹣n)2+(0﹣n﹣1)2=2n2﹣6n+17,
DM2=(0﹣n)2+(1﹣n﹣1)2=2n2,
BD2=42+12=17,
∵以点B、D、M、N为顶点的四边形是菱形,
∴分两种情况:BD为边时或BD为对角线,
①当BD为边时,MN=DM=BD(如图2)或MN=BM=BD(如图3),
∴DM2=BD2=17或BM2=BD2=17,即2n2=17或2n2﹣6n+17=17,
解得:n=±或n=0(舍去)或n=3,
∴M(,)或M(﹣,)或M(3,4),
②如图4,当BD为对角线时,设BD的中点为Q,则Q(2,),
∵四边形BMDN是菱形,
∴MN⊥BD,QB=QD=BD,
∴QD2+QM2=DM2,
∴(2﹣0)2+(﹣1)2+(n﹣2)2+(n+1﹣)2=2n2,
解得:n=,
∴M(,),
综上所述,点M的坐标为(,)或(﹣,)或(3,4)或(,).
4.【解答】解:(1)c=3,点B(3,0),
将点B的坐标代入抛物线表达式:y=ax2+2x+3并解得:a=﹣1,
故抛物线的表达式为:y=﹣x2+2x+3…①;
(2)如图1,过点D作DH⊥x轴于点H,交CB于点M,
S△COF:S△CDF=3:2,则OF:FD=3:2,
∵DH∥CO,故CO:DM=3:2,则DM=CO=2,
由B、C的坐标得:直线BC的表达式为:y=﹣x+3,
设点D(x,﹣x2+2x+3),则点M(x,﹣x+3),
DM=﹣x2+2x+3﹣(﹣x+3)=2,
解得:x=1或2,
故点D(1,4)或(2,3);
(3)①当点P在x轴上方时,
取OG=OE,连接BG,过点B作直线PB交抛物线于点P,交y轴于点M,使∠GBM=∠GBO,
则∠OBP=2∠OBE,过点G作GH⊥BM,
设MH=x,则MG=,
则△OBM中,OB2+OM2=MB2,
即(+)2+9=(x+3)2,解得:x=2,
故MG==,则点M(0,4),
将点B、M的坐标代入一次函数表达式并解得:
直线BM的表达式为:y=﹣x+4…②,
联立①②并解得:x=3(舍去)或,
故点P(,);
②当点P在x轴下方时,
同理可得:点P(﹣,﹣);
综上,点P的坐标(,)或(﹣,﹣).
5.【解答】解:(1)∵抛物线y=﹣x2+bx+3经过B(1,0),
∴﹣1+b+3=0,
解得:b=﹣2,
∴抛物线的表达式为:y=﹣x2﹣2x+3,
∵y=﹣x2﹣2x+3=﹣(x+1)2+4,
∴顶点D的坐标为(﹣1,4);
(2)在y=﹣x2﹣2x+3中,令x=0,得:y=3,
∴C(0,3),
设直线AC解析式为:y=kx+c,
∵A(﹣3,0),C(0,3),
∴,
解得:,
∴直线AC解析式为:y=x+3,
设P(m,﹣m2﹣2m+3),
过点D作DG⊥x轴交直线AC于点G,过点P作PH⊥x轴交直线AC于点H,
∴D(﹣1,4),G(﹣1,2),H(m,m+3),
∴DG=4﹣2=2,PH=﹣m2﹣2m+3﹣(m+3)=﹣m2﹣3m,
∴S△ACD= DG 3=×2=3,S△ACP= PH 3=(﹣m2﹣3m),
∵S△ACP=S△ACD,
∴(﹣m2﹣3m)=×3,
解得:m1=,m2=,
∴P1(,),P2(,);
(3)如图2,过点D作DE⊥y轴于点E,
∵A(﹣3,0),B(1,0),C(0,3),D(﹣1,4),
∴E(0,4),
∴OA=OC=3,CE=DE=1,
∵∠CED=∠AOC=90°,
∴△AOC和△CED都是等腰直角三角形,
∴∠ACO=∠DCE=45°,AC=OA=3,CD=CE=,
∴∠ACD=90°,
连接BC,在△COB中,∠BOC=90°,OB=1,OC=3,
∴=,==,
∴=,∠BOC=∠ACD,
∴△COB∽△ACD,
∴点M在O点处时符合题意,即M1(0,0),
过点C作CM2⊥BC交x轴于点M2,
∴∠BCM2=∠BOC=90°,
∴∠BCO+∠CBO=∠BCO+∠OCM2=90°,
∴∠CBO=∠OCM2,
∴△CBO∽△OCM2,
∴∠BM2C=∠BCO,
∵∠COM2=∠COB=90°,
∴△M2OC∽△COB,
∴==,
∴OM2=3OC=9,
∴M2(﹣9,0),
过点B作BM3⊥BC交y轴于点M3,
∴∠CBM3=∠COB=∠BOM3=90°,
∴∠CBO+∠BCO=∠CBO+∠OBM3=90°,
∴∠BCO=∠OBM3,
∴△BOM3∽△COB,
∴==,
∴OM3=OB=,
∴M3(0,﹣),
∵△COB∽△ACD,
∴△M2OC∽△ACD∽△BOM3,
∴点M的坐标为:(0,0)或(﹣9,0)或(0,﹣).
6.【解答】解:(1)∵y=﹣(x+3)(x﹣4)与x轴交于A、B两点,与y轴交于点C,
∴A(﹣3,0),B(4,0),C(0,4).
(2)将△BPC绕点B顺时针旋转60°得到△BP'C',连接PP',CC',
∴BP=BP',BC=BC,∠PBP'=60°,∠CBC′=60°,PC=P'C′,
∴△BPP'和△BCC′为等边三角形,
∴BC′=BC,PP′=BP,
当O,P,P',C′四点共线,OP+BP+CP的值最小,
∴tan∠OBC===,
∴∠OBC=30°,
∴BC=2OC=8,
∴BC′=BC=8,
∵∠OBC′=∠OBC+∠CBC′=30°+60°=90°,
∴OC′==,
∴OP+BP+CP=OP+PP'+C'P'=OC′=4.
(3)需要分类讨论:
①如图,当CE=CF,且点F在点C左侧时,过点F作FG⊥CE于点G,则△CFG∽△CAO,
∵OA=3,OC=4,
∴AC=5,
∴FG:GC:FC=OA:OC:AC=3:4:5,
设FG=3m,则CG=4m,FC=5m,
∴CE=FC=5m,
∴GE=m,OE=4﹣5m,
∵△FGE∽△DOE,
∴,
∴,
∴m=,
∴CE=5m=;
当点F在点C右侧时,如图所示,过点F作FG⊥y轴于点G,
则△FCG∽△ACO,
∴FG:GC:FC=OA:OC:AC=3:4:5,
设FG=3m,则CG=4m,FC=5m,
∴CE=FC=5m,
∴GE=9m,OE=5m﹣4,
∵△FGE∽△DOE,
∴,
∴,解得m=,
∴CE=5m=16;
②如图,当CE=EF时,过点A作AG∥EF交y轴于点G,由EF=CE,可得,AG=CG,
设OG=m,则AG=CG=4﹣m,
∵OA2+OG2=AG2,
∴32+m2=(4﹣m)2,解得,m=.
由A(﹣3,0)和G(0,),可得直线AG的解析式为:y=x+,
设直线DF为:y=x+b,将D(4,0)代入得:b=﹣,
∴E(0,﹣),
∴CE=4+=.
③如图,当CF=EF时,过点C作CG∥DE交x轴于点G,则∠GCO=∠ACO,
∴OG=OA=3,
∴G(3,0),
由G(3,0),C(0,4)可得直线CG的解析式为:y=﹣x+4,
设直线DE为:y=﹣x+n,将D(4,0)代入得:n=,
∴E(0,),
∴CE=﹣4=.
故CE的长为:或或或16.
7.【解答】解:(1)由题意得:,
解得:,
∴抛物线解析式为y=﹣x2+2x+3;
(2)∵A(0,3),D(2,3),
∴抛物线对称轴为x=1,
∴E(3,0),
设直线AE的解析式为y=kx+3,
∴3k+3=0,解得,k=﹣1,
∴直线AE的解析式为y=﹣x+3,
如图1,作PM∥y轴,交直线AE于点M,设P(t,﹣t2+2t+3),M(t,﹣t+3),
∴PM=﹣t2+2t+3+t﹣3=﹣t2+3t,
∴==,
∴t=时,△PAE的面积最大,最大值是.
(3)由图可知∠PEA≠90°,
∴只能有∠PAE=90°或∠APE=90°,
①当∠PAE=90°时,如图2,作PG⊥y轴,
∵OA=OE,
∴∠OAE=∠OEA=45°,
∴∠PAG=∠APG=45°,
∴PG=AG,
∴t=﹣t2+2t+3﹣3,即﹣t2+t=0,解得t=1或t=0(舍去),
②当∠APE=90°时,如图3,作PK⊥x轴,AQ⊥PK,
则PK=﹣t2+2t+3,AQ=t,KE=3﹣t,PQ=﹣t2+2t+3﹣3=﹣t2+2t,
∵∠APQ+∠KPE=∠APQ+∠PAQ=90°,
∴∠PAQ=∠KPE,且∠PKE=∠PQA,
∴△PKE∽△AQP,
∴,
∴,
即t2﹣t﹣1=0,解得:t=或t=<0(舍去),
综上可知存在满足条件的点P,t的值为1或.
8.【解答】解:(1)∵A(﹣4,0),且AO=4BO,
∴OB=OA=1,
∴B(1,0).
把A(﹣4,0)、B(1,0)代入y=x2+bx+c,
得,解得,
∴抛物线的函数表达式为y=x2+x﹣3;
(2)存在.
由抛物线y=x2+x﹣3与y轴交于点C,得C(0,﹣3);
∵以A,C,E,P为顶点的平行四边形以AC为一边,
∴点P到x轴的距离与点C到x轴的距离相等.
如图1,点P在x轴的下方,
则x2+x﹣3=﹣3,
解得x1=﹣3,x2=0(不符合题意,舍去),
∴点P的坐标为(﹣3,﹣3),
如图2,点P在x轴的上方,
则x2+x﹣3=3,
解得x1=,x2=.
∴点P的坐标为(,3)或(,0).
综上所述,点P的坐标为(﹣3,﹣3)或(,3)或(,0).
9.【解答】解:(1)∵抛物线y=ax2+bx+3与x轴交于点A(﹣1,0)且抛物线的对称轴是直线x=1,
∴,
解得:,
∴抛物线的表达式为:y=﹣x2+2x+3;
令y=0,则﹣x2+2x+3=0,
解得:x1=﹣1,x2=3,
∴B(3,0),
(2)令抛物线y=﹣x2+2x+3中,x=0,则y=3,
即,C(0,3),在Rt△AOC中,AO=1,CO=3,
因此,tan∠ACO==,
(3)如图所示,过点C作MN⊥BC交BP于M、N点,即点P分别位于线段BC的上方或下方,
①当P位于线段BC的上方,过N作y轴垂线交于E点,
∵0C=BC=3,
∴BC=3,
∴△COB为等腰直角三角形,
而MN⊥BC,
∴△COB∽△NEC,
故△NEC也为等腰直角三角形,
∵tan∠ACO=tan∠NBC==,
∴NC=,
∴NE=EC=1,
故N(1,4),而(1,4)刚好为抛物线顶点坐标,即N与P重合,
∴P(1,4),
②当P位于线段BC的下方,过M作y轴垂线交于F点,
∵tan∠ACO=tan∠MBC==,
∴MC=,
而EN∥MF,
∴∠CMF=45°,即△CMF也为等腰直角三角形,
∵MF=CF=1,
∴M(﹣1,2),
而点P'在直线MB上且与抛物线相交,
∴设直线MB的解析式为y=kx+b,将B、M坐标代入得:
,
解得:,
∴直线MB的解析式为:y=﹣x+,
联立方程:,
解得:或(舍去),
故P'(﹣,),
综上所述,当∠PBC=∠ACO时,点P的坐标为(1,4)或(﹣,).
10.【解答】解:(1)将C(0,﹣6)代入二次函数y=a(x2﹣4mx﹣12m2),
则﹣6=a(0﹣0﹣12m2),
解得a=;
(2)证明:如图1,过点D、E分别作x轴的垂线,垂足为M、N.
由a(x2﹣4mx﹣12m2)=0,
解得x1=﹣2m,x2=6m,
则点A(﹣2m,0),B(6m,0),
∵CD∥AB,
∴点D的坐标为(4m,﹣6),
∵AB平分∠DAE,
∴∠DAM=∠EAN,
∴∠DMA=∠ENA=90°,
∴△ADM∽△AEN,
∴==,
设点E坐标为(x,( x2﹣4mx﹣12m2)),
∴=,
∴x=8m,
∴E(8m,10),
∵AM=AO+OM=2m+4m=6m,AN=AO+ON=2m+8m=10m,
∴==,即为定值.
(3)如图2,记二次函数图象的顶点为F,则F的坐标为(2m,﹣8),过点F作FH⊥x轴于点H,
∵tan∠CGO=,tan∠FGH=,
∴=,即=,
∴OG=6m,
∵GF==8,AD==6,
∴=,
∵=,
∴AD:GF:AE=3:4:5,
∴以线段GF,AD,AE的长度为三边长的三角形是直角三角形,
∴以线段GF,AD,AE的长度为三边长的三角形的面积为GF AD=24(m2+1),
∴24(+1)m2﹣48m﹣72+24=24(m2+1),
∴m=3或m=﹣1,
∵m>0,
∴m=3.
11.【解答】解:(1)∵点A(1,2)在直线y=kx上
∴k=2,即直线为y=2x
∵点A(1,2)在抛物线y=mx2+n上,m=﹣1
∴﹣1+n=2,解得:n=3
∴抛物线解析式为y=﹣x2+3
解得:(即点A)
∴点C坐标为(﹣3,﹣6);
(2)过点A作AM⊥x轴于点M,过点P作PN⊥x轴于点N
∴∠OMA=∠ONP=90°
∵点A在直线y=x上,设A(a,a)(a>0)
∴OM=AM=a,∠AOM=45°
∵点A关于x轴对称点A'(a,﹣a)
∴直线y=x沿着x轴翻折得到直线OA'解析式为y=﹣x,∠PON=∠AOM=45°
∴△AOM、△PON都是等腰直角三角形
∵
∴
∴ON=PN=2a
∴P(2a,﹣2a)
∵点A、P都在抛物线y=mx2+n
∴
①﹣②消去n后整理得:ma=﹣1,即a=﹣
①×4﹣②消去ma2后整理得:n=2a
∴n=﹣
∴mn=﹣2;
(3)过点E作EH⊥x轴于点H
解得:,,
∵点A在第一象限
∴A(1,),OA=,tan∠AOD=
∴∠AOD=60°
∴∠BAE=∠BED=∠AOD=60°
设直线AB与x轴交点为F,则△AOF为等边三角形
∴OF=OA=2,F(2,0)
设直线AB解析式为:y=kx+b
解得:
∴直线AB:y=﹣x+2
解得:(即点A)
∴点B与点F重合,点B在x轴上
∴OB=AB=OA=2
∵∠BAE=∠BED,∠BEO=∠BAE+∠ABE=∠BED+∠OED
∴∠ABE=∠OED
∵∠BAE=∠AOD
∴△ABE∽△OED
∴ 即
∴t==﹣(s﹣1)2+,故0<t<;
∵OE=s,sin∠EOH==
∴EH=OE=s
∴S2=S△EOD=OD EH=st==
∵
∴S1==
∴S1 S2﹣(S1+)+=﹣[+]+=,
令s(2﹣s)=u,则原式=u2﹣u+=,
∵>0,
∴当u=时,S1 S2﹣(S1+)+的最小值为,
此时,s(2﹣s)=,解得:s1=,s2=,
当s=或时,均满足0<t<;
∴当OE=s1=时,OH=cos60°=,EH=sin60°=,
∴E1(,)
当OE=s2=时,OH=cos60°=,EH=sin60°=,
∴E2(,),
综上所述,E的坐标为:E1(,),E2(,).
12.【解答】解:(1)A(2,y1),B(3,y2),C(4,y3)为一次函数y=kx+2的图象上以B为等差中心的等差点,理由如下:
∵点A(2,y1),B(3,y2),C(4,y3)为一次函数y=kx+2的图象上的点,
∴y1=2k+2,y2=3k+2,y3=3k+2.
∵y2﹣y1=k=y3﹣y2,
∴A(2,y1),B(3,y2),C(4,y3)为一次函数y=kx+2的图象上以B为等差中心的等差点.
(2)y1=,y2=,y3=,
∴y2﹣y1=﹣=|m|,y3﹣y2=﹣=|m|,
∴|m|=|m|,
∴=2,
∵A(x1,y1)、C(x3,y3)为反比例函数与一次函数y=nx+3的交点,
∴,
∴nx2+3x﹣|m|=0,
∴x1+x3=﹣,x1x3=﹣,△=9+4n|m|>0,
又因为=2,
∵2y2=y1+y3,
∴2y2=n(x1+x3)+6,
∴2=n(x1+x3)+6=﹣3+6=3,
∴x2=,
∴y3=,
∴x2=,
∴y2=,
∵B到原点的距离为,
∴m2+=3,
∴m=±,
∴△=9+4n|m|=9+3n>0,
∴n>﹣,
∴n的取值范围n>﹣且n≠0;
(3)①直线y=x与抛物线y=ax2﹣2ax+b(b>2)交于A(x1,y1)、C(x3,y3),
∴ax2﹣2ax+b=x,
ax2﹣2ax﹣x+b=0,
∴x1+x3=,
又∵点B(x2,y2)在直线y=x上,且为A、C的等差中心.
∴2y2=2x2=,
∴x2=,
∵0<x2<x3<,
∴<,
∴0<a<,
∴x2==1+>2,
∴2<x2<.
②=﹣x22+6b+2015=﹣x22+12ax2+2015=﹣(x2﹣6a)2+2015+36a2,
∴s能取得最大值,
∴s的最大值为2015+36a2,
∵0<a<,
∴2015<2015+36a2<2024,
∴s的最大值的取值范围是2015<2015+36a2<2024.
13.【解答】解:(1)∵y=kx﹣8k(k<0)与x轴,y轴分别交于A、B两点,
∴点A(8,0),点B(0,﹣8k)
∵∠BAO=30°
∴tan∠BAO==
即=
∴k=﹣
即点B(0,),BO=
∴直线解析式y=﹣x+
∵将直线l沿x轴翻折交y轴于点C
∴AC=AB,∠BAO=∠CAO=30°
∴∠BAC=60°
∴△ABC是等边三角形,且BD⊥AC
∴∠CBD=30°=∠ABD
∴BO=OE
∴OE=
∴点E(,0)
(2)∵翻折
∴∠BAO=∠CAO,OB=OC
∵AO⊥BO,BD⊥AC
∴∠OBE+∠BEO=90°,∠CAO+∠AED=90°
∴∠OBE=∠CAO=∠BAO
且∠AOB=∠AOB
∴△BOE∽△AOB
∴,且AB=2BE
∴
∴OB=4=OC
∴BC=OB+OC=8
∴S△ABC=×8×8=32
(3)∵△BOE∽△AOB
∴
∴OE=2,OB=4
∴点A(8,0),点B(0,4),点E(2,0)
∵抛物线y1经过A、B、E三点,其二次项系数为m;
∴设y1=m(x﹣2)(x﹣8)过点B
∴4=16m
∴m=
∵点O(0,0),点E(2,0)
∴线段OE的中点(1,0)
∵抛物线y2=ax2+bx+c过线段OE中点;且5a+3b+2c=0;
∴
解得:
∴抛物线y2=ax2+bx+c=ax2﹣3ax+2a=a(x﹣1)(x﹣2)
∴对称轴为直线x=
∵当≤x≤时,函数y2有最大值m;
∴当≤x≤2时,函数y2有最大值;
若a>0时,当x=时,函数y2有最大值.
∴a(﹣1)(﹣2)=
∴a=
若a<0时,当x=,函数y2有最大值.
∴a(﹣1)(﹣2)=
∴a=﹣1
综上所述:a=﹣或﹣1
14.【解答】解:(1)∵OB=OC,∴点B(3,0),
则抛物线的表达式为:y=a(x+1)(x﹣3)=a(x2﹣2x﹣3)=ax2﹣2ax﹣3a,
故﹣3a=3,解得:a=﹣1,
故抛物线的表达式为:y=﹣x2+2x+3…①,
函数的对称轴为:x=1;
(2)四边形ACDE的周长=AC+DE+CD+AE,其中AC=、DE=1是常数,
故CD+AE最小时,周长最小,
取点C关于函数对称点C′(2,3),则CD=C′D,
取点A′(﹣1,1),则A′D=AE,
故:CD+AE=A′D+DC′,则当A′、D、C′三点共线时,CD+AE=A′D+DC′最小,周长也最小,
四边形ACDE的周长的最小值=AC+DE+CD+AE=+A′D+DC′=+A′C′=+;
(3)如图,设直线CP交x轴于点E,
直线CP把四边形CBPA的面积分为3:5两部分,
又∵S△PCB:S△PCA=EB×(yC﹣yP):AE×(yC﹣yP)=BE:AE,
则BE:AE=3:5或5:3,
则AE=或,
即:点E的坐标为(,0)或(,0),
将点E的坐标代入直线CP的表达式:y=kx+3,
解得:k=﹣6或﹣2,
故直线CP的表达式为:y=﹣2x+3或y=﹣6x+3…②
联立①②并解得:x=4或8(不合题意值已舍去),
故点P的坐标为(4,﹣5)或(8,﹣45).
15.【解答】解:(1)设A(m,n),
∵AO=,
∴m2+n2=5,
∵一次函数y=2x的图象经过A点,
∴n=2m,
∴m2+(2m)2=5,解得m=±1,
∵A在第一象限,
∴m=1,
∴A(1,2),
∵点A在反比例函数y=(k>0)的图象上,
∴k=1×2=2;
(2)连接BP,
由对称性得:OA=OB,
∵Q是AP的中点,
∴OQ=BP,
∵OQ长的最大值为,
∴BP长的最大值为×2=3,
如图2,当BP过圆心C时,BP最长,过B作BD⊥x轴于D,
∵CP=1,
∴BC=2,
∵B在直线y=2x上,
设B(t,2t),则CD=t﹣(﹣2)=t+2,BD=﹣2t,
在Rt△BCD中,由勾股定理得:BC2=CD2+BD2,
∴22=(t+2)2+(﹣2t)2,
t=0(舍)或﹣,
∴B(﹣,﹣),
∵点B在反比例函数y=(k>0)的图象上,
∴k=﹣×(﹣)=;
(3)∵抛物线经过点C(﹣2,0),
∴4a﹣2b+c=0,
又∵a+b+c=0,
∴b=a,c=﹣2a,
∴y=ax2+ax﹣2a=a(x+)2﹣a,
∵﹣<a≤x≤a+1或a≤x≤a+1<﹣,
∴当x=a时,取得最大值4a,
则a a2+a a﹣2a=4a,
解得a=﹣3或2(不合题意舍去),
当x=a+1时,取得最大值4a,
则a(a+1)2+a(a+1)﹣2a=4a,
解得a=1或﹣4,
综上所述所求a的值为﹣4或1.
16.【解答】解:(1)∵AB=2,BC=3
∴1<AC<5
①若AB2=BC AC,则AC=
②若BC2=AB AC,则AC=
③若AC2=AB BC=6,则AC=
综上所述,满足条件的AC的长为,,.
(2)①证明:∵AD∥BC
∴∠DAC=∠ACB,∠ADB=∠DBC
∵BD平分∠ABC
∴∠ABD=∠DBC
∴∠ABD=∠ADB
∴AB=AD
∵点A在以BC为直径的圆上
∴∠BAC=90°
∵∠BAC=∠CDA=90°,∠ACB=∠DAC
∴△ABC∽△DCA
∴
∴AC2=BC DA=BC AB
∴△ABC为比例三角形
②∵∠BAC=∠CDA=90°,AB=AD
∴BC2=AB2+AC2,AC2=AD2+CD2=AB2+CD2
∵AD∥BC
∴∠BCD=180°﹣∠ADC=90°
∴BD2=BC2+CD2=AB2+AC2+AC2﹣AB2=2AC2
∴BD=AC
∴
(3)∵y=mx2﹣4mx﹣12m=m(x﹣2)2﹣16m(m<0)
∴抛物线开口向下,顶点C(2,﹣16m)
∵y=0时,mx2﹣4mx﹣12m=0
解得:x1=﹣2,x2=6
∴A(﹣2,0),B(6,0),AB=8
∴AC=BC=
∵△ABC是比例三角形
∴AB2=BC AC或AC2=AB BC
∴AB=AC
∴4=8
解得:m1=(舍去),m2=﹣
∴抛物线解析式为y=﹣x2+x+3=﹣(x﹣2)2+4
∵M(x0,y0)在抛物线上
∴y0≤4
设z=﹣my02﹣40y0+298=4y02﹣40y0+298=4(y0﹣5)2﹣2
∴当y0≤4时,z随x的增大而减小
∴y0=4时,z最小值=4×(4﹣5)2﹣2=4×3﹣2=10
∵n﹣≤z恒成立,即n﹣≤10
∴n的最大值为10+
21世纪教育网(www.21cnjy.com)
同课章节目录
