2025年九年级数学中考三轮冲刺训练反比例函数中几何综合问题(含答案)
文档属性
| 名称 | 2025年九年级数学中考三轮冲刺训练反比例函数中几何综合问题(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 891.2KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-03-30 00:00:00 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
2025年九年级数学中考三轮冲刺训练反比例函数中几何综合问题
一、选择题
1.如图,点A为反比例函数y=﹣(x<0)图象上的一点,连接AO,过点O作OA的垂线与反比例函数y=(x>0)的图象交于点B,则的值为( )
A. B. C. D.
2.如图,在直角坐标系中,菱形OABC的顶点C(3,4),反比例函数图象交线段AB,射线BC于点E,F,连接EF,则S△BEF的值是( )
A.6 B.7 C.8 D.9
3.如图,点A在双曲线y1=(x>0)上,连接AO并延长,交双曲线y2=(x<0)于点B,点C为x轴上一点,且AO=AC,连接BC,若△ABC的面积是6,则k的值为( )
A.2 B.3 C.4 D.5
4.如图,平面直角坐标系中,原点O为正六边形ABCDEF的中心,EF∥x轴,点E在双曲线y=(k为常数,k>0)上,将正六边形ABCDEF向上平移个单位长度,点D恰好落在双曲线上,则k的值为( )
A.4 B.3 C.2 D.3
5.如图,动点P在函数的图象上运动,PM⊥x轴于M,PN⊥y轴于N,线段PM、PN分别与直线AB:y=﹣x+1交于点E、F,则AF BE的值是( )
A.4 B.2 C.1 D.
6.矩形OBAC在平面直角坐标系中的位置如图所示,反比例函数的图象与AB边交于点D,与AC边交于点F,与OA交于点E,OE=2AE,若四边形ODAF的面积为2,则k的值是( )
A. B. C. D.
7.如图,等腰三角形ABC中,AB=AC,反比例函数y=(k≠0)的图象经过点A、B及AC的中点M,BC∥x轴,AB与y轴交于点N.则的值为( )
A. B. C. D.
8.已知:如图,矩形OABC的边OA在x轴的负半轴上,边OC在y轴的正半轴上,且OA=2OC,直线y=x+b过点C,并且交对角线OB于点E,交x轴于点D,反比例函数过点E且交AB于点M,交BC于点N,连接MN、OM、ON,若△OMN的面积是,则a、b的值分别为( )
A.a=2,b=3 B.a=3,b=2 C.a=﹣2,b=3 D.a=﹣3,b=2
二、填空题
9.如图,在平面直角坐标系xOy中,反比例函数的图象与⊙O交于A,B两点,且点A,B都在第一象限.若A(1,2),则点B的坐标为 .
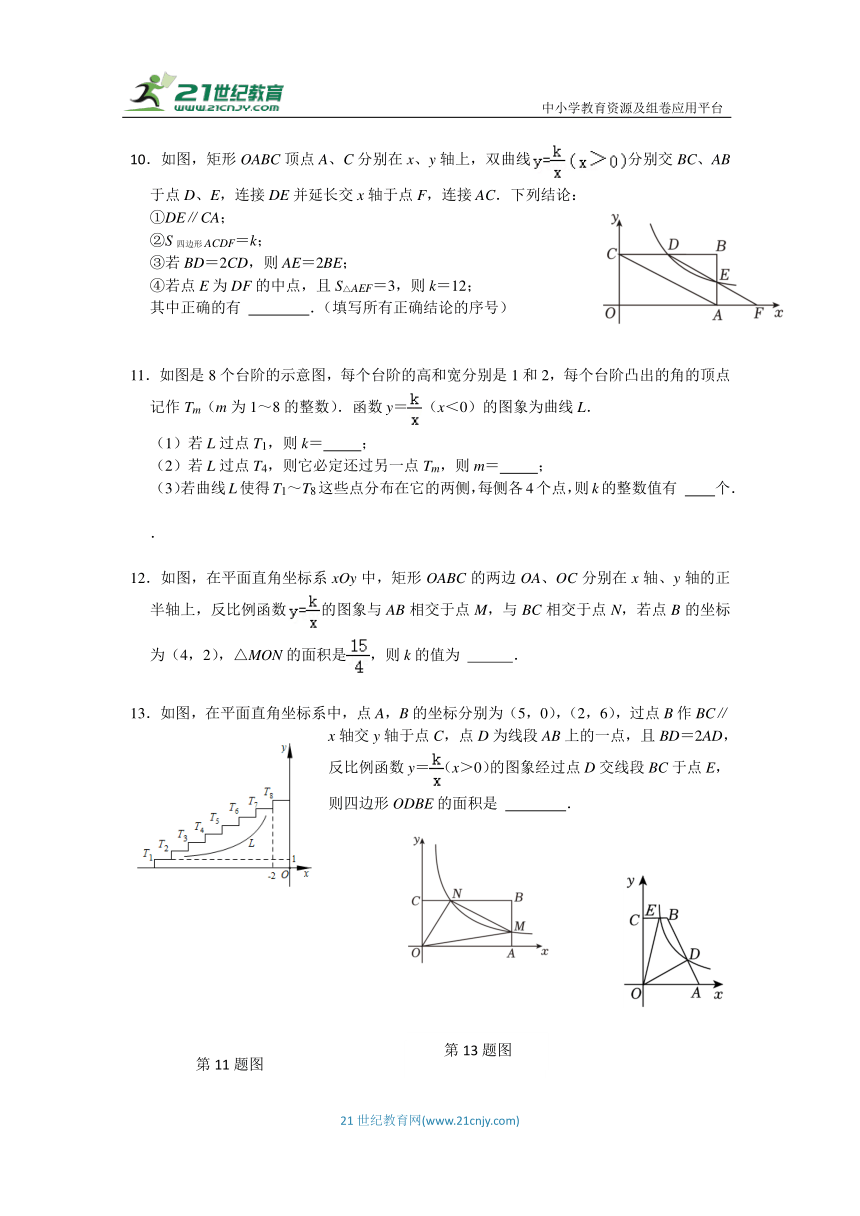
10.如图,矩形OABC顶点A、C分别在x、y轴上,双曲线分别交BC、AB于点D、E,连接DE并延长交x轴于点F,连接AC.下列结论:
①DE∥CA;
②S四边形ACDF=k;
③若BD=2CD,则AE=2BE;
④若点E为DF的中点,且S△AEF=3,则k=12;
其中正确的有 .(填写所有正确结论的序号)
11.如图是8个台阶的示意图,每个台阶的高和宽分别是1和2,每个台阶凸出的角的顶点记作Tm(m为1~8的整数).函数y=(x<0)的图象为曲线L.
(1)若L过点T1,则k= ;
(2)若L过点T4,则它必定还过另一点Tm,则m= ;
(3)若曲线L使得T1~T8这些点分布在它的两侧,每侧各4个点,则k的整数值有 个.
.
12.如图,在平面直角坐标系xOy中,矩形OABC的两边OA、OC分别在x轴、y轴的正半轴上,反比例函数的图象与AB相交于点M,与BC相交于点N,若点B的坐标为(4,2),△MON的面积是,则k的值为 .
13.如图,在平面直角坐标系中,点A,B的坐标分别为(5,0),(2,6),过点B作BC∥x轴交y轴于点C,点D为线段AB上的一点,且BD=2AD,反比例函数y=(x>0)的图象经过点D交线段BC于点E,则四边形ODBE的面积是 .
三、解答题
14.如图,一次函数y=k1x+2的图象与反比例函数y=的图象相交于A(m,4),B两点,与x,y轴分别相交于点C,D.且tan∠ACO=2.
(1)分别求这两个函数的表达式;
(2)以点D为圆心,线段DB的长为半径作弧与x轴正半轴相交于点E,连接AE,BE.求△ABE的面积;
(3)根据函数的图象直接写出关于x的不等式k1x+2>的解集.
15.小军借助反比例函数图象设计“鱼形”图案,如图,在平面直角坐标系中,以反比例函数图象上的点 和点B为顶点,分别作菱形AOCD和菱形OBEF,点D,E在x轴上,以点O为圆心,OA长为半径作,连接BF.
(1)求k的值;
(2)求扇形AOC的半径及圆心角的度数;
(3)请直接写出图中阴影部分面积之和.
16.如图,在平面直角坐标系中,一次函数的图象l与反比例函数y=的图象交于M(,4),N(n,1)两点.
(1)求反比例函数及一次函数的表达式;
(2)求△OMN的面积;
(3)若点P是y轴上一动点,连接PM,PN.当PM+PN的值最小时,求点P的坐标.
17.如图,点M、N是反比例函数的图象上的两个动点,过点M作MP⊥y轴、过点N作NQ⊥x轴,分别交反比例函数的图象于点P、Q,连接PN、QM.设点M的横坐标为m(m>0),点N的横坐标为n(n<0).
(1)若m=3,求MP的长;
(2)若MP=NQ,求mn的值;
(3)①求△MNP的面积(用含m、n的代数式表示);
②点P、Q到直线MN的距离是否相等?并说明理由.
18.如图,在平面直角坐标系xOy中,矩形OABC的顶点A在x轴上,顶点C在y轴上,D是BC的中点,过点D的反比例函数图象交AB于E点,连接DE.若OD=5,tan∠COD=.
(1)求过点D的反比例函数的解析式;
(2)求△DBE的面积;
(3)x轴上是否存在点P使△OPD为直角三角形?若存在,请直接写出P点的坐标;若不存在,请说明理由.
19.如图,△AOB是等边三角形,点B在x轴的正半轴上,OB=4,反比例函数y过AB的中点C,交OA于点E.
(1)求k的值;
(2)以O为圆心OE为半径作圆,⊙O与y的图象的另一个分支交于点D、F.求图中阴影部分面积.
20.如图,反比例函数y(k>0)与长方形OABC在第一象限相交于D、E两点,OA=2,OC=4,连接OD、OE、DE.记△OAD、△OCE的面积分别为S1、S2.
(1)填空:
①点B坐标为 ;
②S1 S2(填“>”、“<”、“=”);
(2)当S1+S2=2时,求:k的值及点D、E的坐标;试判断△ODE的形状,并求△ODE的面积.
参考答案
一、选择题
1.【解答】解:作AG⊥x轴,垂足为G,BH⊥x轴,垂足为H,
∵点A在函数y=﹣图象上,点B在反比例函数y=图象上,
∴S△AGO=,S△BOH=2,
∵∠AOB=90°,
∴∠AOG=∠HBO,∠AGO=∠OHB,
∴△AGO∽△OHB,
∴,
∴.
故选:A.
2.【解答】解:∵C(3,4),
∴OC=BC==5,
∴B(8,4),
在反比例函数y=中,当y=4时,x=2,
F(2,4),
BF=8﹣2=6.
设直线AB的解析式为y=kx+b,A(5,0)、B(8,4)在直线上,
,解得,
∴直线AB的解析式为y=x﹣,
联立方程组,解得,,
∴E(6,),
∴S△BEF==8.
故选:C.
3.【解答】解:如图,过A作AD⊥x轴于D.
由题意,设A(a,)(a>0),
∵AO=AC,AD⊥OC,
∴OC=2OD=2a.
又设直线OA为y=mx,
∴ma=.
∴m=.
∴直线OA为y=x.
联立,
∴x2=.
∴x=±.
∴B(﹣,﹣).
∴S△ABC=S△BOC+S△AOC
=OC |yB|+OC |yA|
=×2a(+)
=k.
又∵S△ABC=6,
∴k=6.
∴k=4.
故选:C.
4.【解答】解:如图,作DG⊥EF交EF的延长线于点G,DG交反比例函数图象于点H,
∵原点O为正六边形ABCDEF的中心,EF∥x轴,
∴∠EDO===60°,
∴∠EDG=30°,
∴EG=ED,GD=,
设正六边形ABCDEF的边长为a,则E(,),H(a,),
∵点E、H都在反比例函数图象上,
∴,
解得a=4,
∴H(4,),
∴k=4.
故选:A.
5.【解答】解:作FG⊥x轴,
∵P的坐标为(a,),且PN⊥OB,PM⊥OA,
∴N的坐标为(0,),M点的坐标为(a,0),
∴BN=1﹣,
在直角三角形BNF中,∠NBF=45°,
∴三角形OAB是等腰直角三角形,
∴OB=OA=1,
∴NF=BN=1﹣,
∴F点的坐标为(1﹣,),
同理可得出E点的坐标为(a,1﹣a),
∴AF2=(1﹣1+)2+()2=,BE2=(a)2+(﹣a)2=2a2,
∴AF2 BE2= 2a2=1,即AF BE=1.
故选:C.
6.【解答】解:过点E作EM⊥OC,则EM∥OB,
∴△OME∽△OCA,
∴,
设,
∵OE=2AE,
∴,
∴,
∴,
即,解得:,
故选:D.
7.【解答】解:作过A作BC的垂线垂足为D,BC与y轴交于E点,如图,
在等腰三角形ABC中,AD⊥BC,D是BC中点,
设,,
由BC中点为D,AB=AC,
在等腰三角形ABC中,
∴BD=DC=a﹣b,
∴,
∵AC的中点为M,
∴,即,
由M在反比例函数上得,
∴,
解得:b=﹣3a,
由题可知,AD∥NE,
∴,
故选:B.
8.【解答】解:过点E作EH⊥AO,垂足为H,如图,
∵直线y=x+b与y轴交于点C,交x轴于点D,
∴点C(0,b),点D(﹣b,0).
∴OC=OD=b.
∵四边形OABC是矩形,OA=2OC,
∴BC=OA=2b,AB=OC=b,BC∥OA.
∴△BEC∽△OED.
∴==2.
∴=3.
∵EH⊥OA,∠COA=90°,
∴∠EHA=∠COA=90°.
∴EH∥OC.
∴△DOC∽△DHE.
∴===3.
∴EH=,DH=.
∴OH=OD﹣DH=b﹣=.
∴点E的坐标为(﹣,).
∵点E在反比例函数上,
∴﹣×=a.
∴2b2=﹣9a.
∵反比例函数图象交AB于点M,交BC于点N,
∴点M的坐标为(﹣2b,),点N的坐标为(,b).
∴S△BMN=BM BN
=(b﹣)[2b﹣(﹣)]
=××
=
=﹣a.
∴S△OMN=S矩形OABC﹣S△AMO﹣S△OCN﹣S△BMN
=2b2﹣(﹣)﹣(﹣)﹣(﹣a)
=﹣9a+a+a
=﹣a=.
解得:a=﹣2.
∴2b2=﹣9a=﹣9×(﹣2)=18.
∴b=±3.
∵b>0,
∴b=3.
故选:C.
二、填空题
9.【解答】解:点A与B关于直线y=x对称,
设直线AB的解析式为y=﹣x+b,将点A(1,2)坐标代入得,
2=﹣1+b,解得b=3,
∴直线AB解析式为y=﹣x+3,
∵点A(1,2)在反比例函数图象上,
∴反比例函数解析式为y=,
联立方程组,解得或.
∴B(2,1).
故答案为:(2,1).
10.【解答】解:设B(m,n),则OA=BC=m,OC=AB=n,
∵双曲线分别交BC、AB于点D、E,
∴D(,n),E(m,),
∴CD=,AE=,
∵,==,
∴,
∴DE∥CA,故①正确;
∵DF∥AC,CD∥AF,
∴四边形ACDF是平行四边形,
∴S四边形ACDF=CD OC=k,故②正确;
∵DE∥CA,
∴,
∵BD=2CD,
∴=2,
∴BE=2AE,故③错误;
∵∠B=∠EAF=90°,∠BED=∠AEF,BE=AE,
∴△BED≌AEF(ASA),
∴AF=BD,S△BDE=S△AEF=3,
∴=3,
∵CD=AF,
∴=3,
∴CD AB=12,
∴k=12,故④正确.
故答案为:①②④.
11.【解答】解:(1)∵每个台阶的高和宽分别是1和2,
∴T1(﹣16,1),T2(﹣14,2),T3(﹣12,3),T4(﹣10,4),T5(﹣8,5),T6(﹣6,6),T7(﹣4,7),T8(﹣2,8),
∵L过点T1,
∴k=﹣16×1=﹣16,
故答案为:﹣16;
(2)∵L过点T4,
∴k=﹣10×4=﹣40,
∴反比例函数解析式为:y=﹣,
当x=﹣8时,y=5,
∴T5在反比例函数图象上,
∴m=5,
故答案为:5;
(3)若曲线L过点T1(﹣16,1),T8(﹣2,8)时,k=﹣16,
若曲线L过点T2(﹣14,2),T7(﹣4,7)时,k=﹣14×2=﹣28,
若曲线L过点T3(﹣12,3),T6(﹣6,6)时,k=﹣12×3=﹣36,
若曲线L过点T4(﹣10,4),T5(﹣8,5)时,k=﹣40,
∵曲线L使得T1~T8这些点分布在它的两侧,每侧各4个点,
∴﹣36<k<﹣28,
∴整数k=﹣35,﹣34,﹣33,﹣32,﹣31,﹣30,﹣29共7个,
故答案为:7.
12.【解答】解:由题意可知点M的坐标为(4,),点N的坐标为(,2,),则BM=2﹣,BN=4﹣,
由反比例函数k值的几何意义可得:S△OCN+S△OAM=k,
∴S△BMN=S矩形OABC﹣k﹣,
=8﹣k﹣,
解得:k=2.
故答案为:2.
13.【解答】解:过点B作BM⊥x轴于M,过点D作DN⊥x轴于N,如图所示:
∵点A(5,0),B(2,6),BC∥x轴,∠COM=90°,
∴四边形OMBC为矩形,
∴BC=OM=2,OC=MB=6,
∴AM=OA﹣OM=5﹣2=3,
∵BD=2AD,
∴AD:AB=1:3,
∵BM⊥x轴,DN⊥x轴,
∴BM∥DN,
∴△ADN∽△ABM,
∴DN:BM=AN:AM=AD:AB,
即DN:6=AN:3=1:3,
∴DN=2,AN=1,
∴ON=OA﹣AN=5﹣1=4,
∴点D的坐标为(4,2),
∵反比例函数(x>0)的图象经过点D,
∴k=8,
根据反比例函数比例系数的几何意义得:S△OCE=×8=4,
∵S梯形OABC=(BC+OA) OC=×(2+5)×6=21,S△AOD=OA DN=×5×2=5,
∴S四边形ODBE=S梯形OABC﹣S△OCE﹣S△AOD=21﹣4﹣5=12.
三、解答题
14.【解答】解:(1)由y=k1x+2得D(0,2),
∵tan∠ACO=2,
∴=2,
∴C(﹣1,0),
代入y=k1x+2得k1=2,
∴一次函数解析式为y=2x+2.
过A作AM⊥x轴,如图1.
∴tan∠ACO==2,
∵AM=4,
∴CM=2,
∴OM=1,
∴A(1,4),
代入y=得k2=4,
∴反比例函数解析式为y=.
(2)如图2:过A作AN∥y轴,交BE于N.
联立y=2x+2和y=得x2+x﹣2=0,
∴x=﹣2或1,
∴B(﹣2,﹣2).
∴BD==2,
∴DE=DB=2,
∴OE==4,
∴E(4,0),
设直线BE解析式为y=mx+n,
∴,
∴m=,n=﹣,
∴直线BE解析式为y=x﹣,
∴N(1,﹣1),
∴△ABE面积=(4+1)(4+2)=15.
(3)看图得:当﹣2<x<0或x>1时,k1x+2>,即2x+2>.
15.【解答】解:(1)将A(,1)代入到y=中,
得:1=,
解得:k=;
(2)过点A作OD 的垂线,交x轴于G,
∵A(,1),
∴AG=1,OG=,
OA==2,
∴半径为2;
∵AG=OA,
∴∠AOG=30°,
由菱形的性质可知,∠AOG=∠COG=30°,
∴∠AOC=60°,
∴圆心角的度数为:60°;
(3)∵OD=2OG=2,
∴S菱形AOCD=AC×OD=2,
∴S扇形AOC=×π×r2=,
在菱形OBEF中,S△FHO=S△BHO,
∵S△FHO==,
∴S△FBO=2×=,
∴S阴影=S△FBO+S菱形AOCD﹣S扇形AOC=+2﹣π=3﹣.
16.【解答】解:(1)由题意,∵M(,4)在反比例函数y=上,
∴k=×4=2.
∴反比例函数表达式为y=.
又N(n,1)在反比例函数y=上,
∴n=2.
∴N(2,1).
设一次函数表达式为y=ax+b,
∴.
∴a=﹣2,b=5.
∴一次函数的表达式为y=﹣2x+5.
(2)由题意,如图,设直线l交x轴于点A,交y轴于点B,
又直线l为y=﹣2x+5,
∴A(,0),B(0,5).
∴OA=,OB=5.
∴S△OMN=S△AOB﹣S△AON﹣S△BOM=×AO×BO﹣×AO yN﹣×BO×xM
=××5﹣××1﹣×5×
=.
(3)由题意,如图,作点M关于y轴的对称点M',连接M'N交y轴于点P,则PM+PN的最小值等于M'N的长.
∵M(,4)与M'关于y轴对称,
∴M'为(﹣,4).
又N(2,1),
∴直线M′N为y=﹣x+.
令x=0,则y=,
∴P(0,).
17.【解答】解:(1)当m=3时,
又点M的横坐标为m,M在y=上,
∴M(3,1).
又MP⊥y轴,
∴P的纵坐标为1.
又∵P在y=﹣上,
∴P(﹣2,1).
∴MP=3﹣(﹣2)=5.
(2)由题意,∵点M的横坐标为m,点N的横坐标为n,M、N都在y=上,
∴M(m,),N(n,).
又MP⊥y轴,NQ⊥x轴,
∴P的纵坐标为,Q的横坐标为n.
又∵P、Q都在y=﹣上,
∴P(﹣,),Q(n,﹣).
∴MP=m﹣(﹣m)=m,NQ=﹣﹣=﹣.
又MP=NQ,
∴=﹣.
∴mn=﹣3.
(3)①由题意,根据(2)N(n,),P(﹣,),
∴△MNP的MP边上的高h为:﹣=.
又∵MP=m,
∴S△MNP=MP h=×m×=.
②相等.理由如下:
由题意,根据(2)M(m,),Q(n,﹣).
∴△MNQ的NQ边上的高h'=m﹣n.
又∵NQ=﹣,
∴S△MNQ=NQ h'=×(m﹣n)×(﹣)=.
又由①S△MNP=,
∴S△MNP=S△MNQ.
∴当MP看作底时,点P、Q到直线MN的距离相等.
18.【解答】解:(1)∵四边形OABC是矩形,
∴BC=OA,AB=OC,
∵tan∠COD=,
∴设OC=3x,CD=4x,
∴OD=5x=5,
∴x=1,
∴OC=3,CD=4,
∴D(4,3),
设过点D的反比例函数的解析式为:y=,
∴k=12,∴反比例函数的解析式为:y=;
(2)∵点D是BC的中点,
∴B(8,3),
∴BC=8,AB=3,
∵E点在过点D的反比例函数图象上,
∴E(8,),
∴S△DBE=BD BE==3;
(3)存在,
∵△OPD为直角三角形,
∴当∠OPD=90°时,PD⊥x轴于P,
∴OP=4,
∴P(4,0),
当∠ODP=90°时,
如图,过D作DH⊥x轴于H,
∴OD2=OH OP,
∴OP==.
∴P(,O),
∴存在点P使△OPD为直角三角形,
∴P(4,0),(,0).
19.【解答】解:(1)如图,连接OC,过点C作CM⊥OB于点M,
∵△OAB是正三角形,OB=4,
∴OC⊥AB,AC=BC=2,
∴OCBC=2,
在Rt△OCM中,∠COM=30°,OC=2,
∴OMOC=3,CMOC,
∴S△COMOM CM|k|,
∵k>0,
∴k=3;
(2)由中心对称图形的性质可知,∠DOF=∠AOC=30°,OD=OF=OC=2,
∴S扇形ODFπ.
20.【解答】解:(1)①根据长方形OABC中,OA=2,OC=4,
则点B坐标为(4,2),
②∵反比例函数(k>0)与长方形OABC在第一象限相交于D、E两点,
利用△OAD、△OCE的面积分别为S1AD AO,S2 CO EC,xy=k,得出,
S1AD AOk,S2 CO ECk,
∴S1=S2;
(2)当S1+S2=2时,∵S1=S2,
∴S1=S2=1,
∴k=2,
∵S1AD AOAD×2=1,
∴AD=1,
∵S2 CO EC4×EC=1,
∴EC,
∵OA=2,OC=4,
∴BD=4﹣1=3,
BE=2,
∴DO2=AO2+AD2=4+1=5,
DE2=DB2+BE2=9,
OE2=CO2+CE2=16,
∴D的坐标为(1,2),E的坐标为(4,)
∴DO2+DE2=OE2,
∴△ODE是直角三角形,
∵DO2=5,
∴DO,
∵DE2,
∴DE,
∴△ODE的面积为:DO×DE,
故答案为:(1)①(4,2);②=.
21世纪教育网(www.21cnjy.com)
2025年九年级数学中考三轮冲刺训练反比例函数中几何综合问题
一、选择题
1.如图,点A为反比例函数y=﹣(x<0)图象上的一点,连接AO,过点O作OA的垂线与反比例函数y=(x>0)的图象交于点B,则的值为( )
A. B. C. D.
2.如图,在直角坐标系中,菱形OABC的顶点C(3,4),反比例函数图象交线段AB,射线BC于点E,F,连接EF,则S△BEF的值是( )
A.6 B.7 C.8 D.9
3.如图,点A在双曲线y1=(x>0)上,连接AO并延长,交双曲线y2=(x<0)于点B,点C为x轴上一点,且AO=AC,连接BC,若△ABC的面积是6,则k的值为( )
A.2 B.3 C.4 D.5
4.如图,平面直角坐标系中,原点O为正六边形ABCDEF的中心,EF∥x轴,点E在双曲线y=(k为常数,k>0)上,将正六边形ABCDEF向上平移个单位长度,点D恰好落在双曲线上,则k的值为( )
A.4 B.3 C.2 D.3
5.如图,动点P在函数的图象上运动,PM⊥x轴于M,PN⊥y轴于N,线段PM、PN分别与直线AB:y=﹣x+1交于点E、F,则AF BE的值是( )
A.4 B.2 C.1 D.
6.矩形OBAC在平面直角坐标系中的位置如图所示,反比例函数的图象与AB边交于点D,与AC边交于点F,与OA交于点E,OE=2AE,若四边形ODAF的面积为2,则k的值是( )
A. B. C. D.
7.如图,等腰三角形ABC中,AB=AC,反比例函数y=(k≠0)的图象经过点A、B及AC的中点M,BC∥x轴,AB与y轴交于点N.则的值为( )
A. B. C. D.
8.已知:如图,矩形OABC的边OA在x轴的负半轴上,边OC在y轴的正半轴上,且OA=2OC,直线y=x+b过点C,并且交对角线OB于点E,交x轴于点D,反比例函数过点E且交AB于点M,交BC于点N,连接MN、OM、ON,若△OMN的面积是,则a、b的值分别为( )
A.a=2,b=3 B.a=3,b=2 C.a=﹣2,b=3 D.a=﹣3,b=2
二、填空题
9.如图,在平面直角坐标系xOy中,反比例函数的图象与⊙O交于A,B两点,且点A,B都在第一象限.若A(1,2),则点B的坐标为 .
10.如图,矩形OABC顶点A、C分别在x、y轴上,双曲线分别交BC、AB于点D、E,连接DE并延长交x轴于点F,连接AC.下列结论:
①DE∥CA;
②S四边形ACDF=k;
③若BD=2CD,则AE=2BE;
④若点E为DF的中点,且S△AEF=3,则k=12;
其中正确的有 .(填写所有正确结论的序号)
11.如图是8个台阶的示意图,每个台阶的高和宽分别是1和2,每个台阶凸出的角的顶点记作Tm(m为1~8的整数).函数y=(x<0)的图象为曲线L.
(1)若L过点T1,则k= ;
(2)若L过点T4,则它必定还过另一点Tm,则m= ;
(3)若曲线L使得T1~T8这些点分布在它的两侧,每侧各4个点,则k的整数值有 个.
.
12.如图,在平面直角坐标系xOy中,矩形OABC的两边OA、OC分别在x轴、y轴的正半轴上,反比例函数的图象与AB相交于点M,与BC相交于点N,若点B的坐标为(4,2),△MON的面积是,则k的值为 .
13.如图,在平面直角坐标系中,点A,B的坐标分别为(5,0),(2,6),过点B作BC∥x轴交y轴于点C,点D为线段AB上的一点,且BD=2AD,反比例函数y=(x>0)的图象经过点D交线段BC于点E,则四边形ODBE的面积是 .
三、解答题
14.如图,一次函数y=k1x+2的图象与反比例函数y=的图象相交于A(m,4),B两点,与x,y轴分别相交于点C,D.且tan∠ACO=2.
(1)分别求这两个函数的表达式;
(2)以点D为圆心,线段DB的长为半径作弧与x轴正半轴相交于点E,连接AE,BE.求△ABE的面积;
(3)根据函数的图象直接写出关于x的不等式k1x+2>的解集.
15.小军借助反比例函数图象设计“鱼形”图案,如图,在平面直角坐标系中,以反比例函数图象上的点 和点B为顶点,分别作菱形AOCD和菱形OBEF,点D,E在x轴上,以点O为圆心,OA长为半径作,连接BF.
(1)求k的值;
(2)求扇形AOC的半径及圆心角的度数;
(3)请直接写出图中阴影部分面积之和.
16.如图,在平面直角坐标系中,一次函数的图象l与反比例函数y=的图象交于M(,4),N(n,1)两点.
(1)求反比例函数及一次函数的表达式;
(2)求△OMN的面积;
(3)若点P是y轴上一动点,连接PM,PN.当PM+PN的值最小时,求点P的坐标.
17.如图,点M、N是反比例函数的图象上的两个动点,过点M作MP⊥y轴、过点N作NQ⊥x轴,分别交反比例函数的图象于点P、Q,连接PN、QM.设点M的横坐标为m(m>0),点N的横坐标为n(n<0).
(1)若m=3,求MP的长;
(2)若MP=NQ,求mn的值;
(3)①求△MNP的面积(用含m、n的代数式表示);
②点P、Q到直线MN的距离是否相等?并说明理由.
18.如图,在平面直角坐标系xOy中,矩形OABC的顶点A在x轴上,顶点C在y轴上,D是BC的中点,过点D的反比例函数图象交AB于E点,连接DE.若OD=5,tan∠COD=.
(1)求过点D的反比例函数的解析式;
(2)求△DBE的面积;
(3)x轴上是否存在点P使△OPD为直角三角形?若存在,请直接写出P点的坐标;若不存在,请说明理由.
19.如图,△AOB是等边三角形,点B在x轴的正半轴上,OB=4,反比例函数y过AB的中点C,交OA于点E.
(1)求k的值;
(2)以O为圆心OE为半径作圆,⊙O与y的图象的另一个分支交于点D、F.求图中阴影部分面积.
20.如图,反比例函数y(k>0)与长方形OABC在第一象限相交于D、E两点,OA=2,OC=4,连接OD、OE、DE.记△OAD、△OCE的面积分别为S1、S2.
(1)填空:
①点B坐标为 ;
②S1 S2(填“>”、“<”、“=”);
(2)当S1+S2=2时,求:k的值及点D、E的坐标;试判断△ODE的形状,并求△ODE的面积.
参考答案
一、选择题
1.【解答】解:作AG⊥x轴,垂足为G,BH⊥x轴,垂足为H,
∵点A在函数y=﹣图象上,点B在反比例函数y=图象上,
∴S△AGO=,S△BOH=2,
∵∠AOB=90°,
∴∠AOG=∠HBO,∠AGO=∠OHB,
∴△AGO∽△OHB,
∴,
∴.
故选:A.
2.【解答】解:∵C(3,4),
∴OC=BC==5,
∴B(8,4),
在反比例函数y=中,当y=4时,x=2,
F(2,4),
BF=8﹣2=6.
设直线AB的解析式为y=kx+b,A(5,0)、B(8,4)在直线上,
,解得,
∴直线AB的解析式为y=x﹣,
联立方程组,解得,,
∴E(6,),
∴S△BEF==8.
故选:C.
3.【解答】解:如图,过A作AD⊥x轴于D.
由题意,设A(a,)(a>0),
∵AO=AC,AD⊥OC,
∴OC=2OD=2a.
又设直线OA为y=mx,
∴ma=.
∴m=.
∴直线OA为y=x.
联立,
∴x2=.
∴x=±.
∴B(﹣,﹣).
∴S△ABC=S△BOC+S△AOC
=OC |yB|+OC |yA|
=×2a(+)
=k.
又∵S△ABC=6,
∴k=6.
∴k=4.
故选:C.
4.【解答】解:如图,作DG⊥EF交EF的延长线于点G,DG交反比例函数图象于点H,
∵原点O为正六边形ABCDEF的中心,EF∥x轴,
∴∠EDO===60°,
∴∠EDG=30°,
∴EG=ED,GD=,
设正六边形ABCDEF的边长为a,则E(,),H(a,),
∵点E、H都在反比例函数图象上,
∴,
解得a=4,
∴H(4,),
∴k=4.
故选:A.
5.【解答】解:作FG⊥x轴,
∵P的坐标为(a,),且PN⊥OB,PM⊥OA,
∴N的坐标为(0,),M点的坐标为(a,0),
∴BN=1﹣,
在直角三角形BNF中,∠NBF=45°,
∴三角形OAB是等腰直角三角形,
∴OB=OA=1,
∴NF=BN=1﹣,
∴F点的坐标为(1﹣,),
同理可得出E点的坐标为(a,1﹣a),
∴AF2=(1﹣1+)2+()2=,BE2=(a)2+(﹣a)2=2a2,
∴AF2 BE2= 2a2=1,即AF BE=1.
故选:C.
6.【解答】解:过点E作EM⊥OC,则EM∥OB,
∴△OME∽△OCA,
∴,
设,
∵OE=2AE,
∴,
∴,
∴,
即,解得:,
故选:D.
7.【解答】解:作过A作BC的垂线垂足为D,BC与y轴交于E点,如图,
在等腰三角形ABC中,AD⊥BC,D是BC中点,
设,,
由BC中点为D,AB=AC,
在等腰三角形ABC中,
∴BD=DC=a﹣b,
∴,
∵AC的中点为M,
∴,即,
由M在反比例函数上得,
∴,
解得:b=﹣3a,
由题可知,AD∥NE,
∴,
故选:B.
8.【解答】解:过点E作EH⊥AO,垂足为H,如图,
∵直线y=x+b与y轴交于点C,交x轴于点D,
∴点C(0,b),点D(﹣b,0).
∴OC=OD=b.
∵四边形OABC是矩形,OA=2OC,
∴BC=OA=2b,AB=OC=b,BC∥OA.
∴△BEC∽△OED.
∴==2.
∴=3.
∵EH⊥OA,∠COA=90°,
∴∠EHA=∠COA=90°.
∴EH∥OC.
∴△DOC∽△DHE.
∴===3.
∴EH=,DH=.
∴OH=OD﹣DH=b﹣=.
∴点E的坐标为(﹣,).
∵点E在反比例函数上,
∴﹣×=a.
∴2b2=﹣9a.
∵反比例函数图象交AB于点M,交BC于点N,
∴点M的坐标为(﹣2b,),点N的坐标为(,b).
∴S△BMN=BM BN
=(b﹣)[2b﹣(﹣)]
=××
=
=﹣a.
∴S△OMN=S矩形OABC﹣S△AMO﹣S△OCN﹣S△BMN
=2b2﹣(﹣)﹣(﹣)﹣(﹣a)
=﹣9a+a+a
=﹣a=.
解得:a=﹣2.
∴2b2=﹣9a=﹣9×(﹣2)=18.
∴b=±3.
∵b>0,
∴b=3.
故选:C.
二、填空题
9.【解答】解:点A与B关于直线y=x对称,
设直线AB的解析式为y=﹣x+b,将点A(1,2)坐标代入得,
2=﹣1+b,解得b=3,
∴直线AB解析式为y=﹣x+3,
∵点A(1,2)在反比例函数图象上,
∴反比例函数解析式为y=,
联立方程组,解得或.
∴B(2,1).
故答案为:(2,1).
10.【解答】解:设B(m,n),则OA=BC=m,OC=AB=n,
∵双曲线分别交BC、AB于点D、E,
∴D(,n),E(m,),
∴CD=,AE=,
∵,==,
∴,
∴DE∥CA,故①正确;
∵DF∥AC,CD∥AF,
∴四边形ACDF是平行四边形,
∴S四边形ACDF=CD OC=k,故②正确;
∵DE∥CA,
∴,
∵BD=2CD,
∴=2,
∴BE=2AE,故③错误;
∵∠B=∠EAF=90°,∠BED=∠AEF,BE=AE,
∴△BED≌AEF(ASA),
∴AF=BD,S△BDE=S△AEF=3,
∴=3,
∵CD=AF,
∴=3,
∴CD AB=12,
∴k=12,故④正确.
故答案为:①②④.
11.【解答】解:(1)∵每个台阶的高和宽分别是1和2,
∴T1(﹣16,1),T2(﹣14,2),T3(﹣12,3),T4(﹣10,4),T5(﹣8,5),T6(﹣6,6),T7(﹣4,7),T8(﹣2,8),
∵L过点T1,
∴k=﹣16×1=﹣16,
故答案为:﹣16;
(2)∵L过点T4,
∴k=﹣10×4=﹣40,
∴反比例函数解析式为:y=﹣,
当x=﹣8时,y=5,
∴T5在反比例函数图象上,
∴m=5,
故答案为:5;
(3)若曲线L过点T1(﹣16,1),T8(﹣2,8)时,k=﹣16,
若曲线L过点T2(﹣14,2),T7(﹣4,7)时,k=﹣14×2=﹣28,
若曲线L过点T3(﹣12,3),T6(﹣6,6)时,k=﹣12×3=﹣36,
若曲线L过点T4(﹣10,4),T5(﹣8,5)时,k=﹣40,
∵曲线L使得T1~T8这些点分布在它的两侧,每侧各4个点,
∴﹣36<k<﹣28,
∴整数k=﹣35,﹣34,﹣33,﹣32,﹣31,﹣30,﹣29共7个,
故答案为:7.
12.【解答】解:由题意可知点M的坐标为(4,),点N的坐标为(,2,),则BM=2﹣,BN=4﹣,
由反比例函数k值的几何意义可得:S△OCN+S△OAM=k,
∴S△BMN=S矩形OABC﹣k﹣,
=8﹣k﹣,
解得:k=2.
故答案为:2.
13.【解答】解:过点B作BM⊥x轴于M,过点D作DN⊥x轴于N,如图所示:
∵点A(5,0),B(2,6),BC∥x轴,∠COM=90°,
∴四边形OMBC为矩形,
∴BC=OM=2,OC=MB=6,
∴AM=OA﹣OM=5﹣2=3,
∵BD=2AD,
∴AD:AB=1:3,
∵BM⊥x轴,DN⊥x轴,
∴BM∥DN,
∴△ADN∽△ABM,
∴DN:BM=AN:AM=AD:AB,
即DN:6=AN:3=1:3,
∴DN=2,AN=1,
∴ON=OA﹣AN=5﹣1=4,
∴点D的坐标为(4,2),
∵反比例函数(x>0)的图象经过点D,
∴k=8,
根据反比例函数比例系数的几何意义得:S△OCE=×8=4,
∵S梯形OABC=(BC+OA) OC=×(2+5)×6=21,S△AOD=OA DN=×5×2=5,
∴S四边形ODBE=S梯形OABC﹣S△OCE﹣S△AOD=21﹣4﹣5=12.
三、解答题
14.【解答】解:(1)由y=k1x+2得D(0,2),
∵tan∠ACO=2,
∴=2,
∴C(﹣1,0),
代入y=k1x+2得k1=2,
∴一次函数解析式为y=2x+2.
过A作AM⊥x轴,如图1.
∴tan∠ACO==2,
∵AM=4,
∴CM=2,
∴OM=1,
∴A(1,4),
代入y=得k2=4,
∴反比例函数解析式为y=.
(2)如图2:过A作AN∥y轴,交BE于N.
联立y=2x+2和y=得x2+x﹣2=0,
∴x=﹣2或1,
∴B(﹣2,﹣2).
∴BD==2,
∴DE=DB=2,
∴OE==4,
∴E(4,0),
设直线BE解析式为y=mx+n,
∴,
∴m=,n=﹣,
∴直线BE解析式为y=x﹣,
∴N(1,﹣1),
∴△ABE面积=(4+1)(4+2)=15.
(3)看图得:当﹣2<x<0或x>1时,k1x+2>,即2x+2>.
15.【解答】解:(1)将A(,1)代入到y=中,
得:1=,
解得:k=;
(2)过点A作OD 的垂线,交x轴于G,
∵A(,1),
∴AG=1,OG=,
OA==2,
∴半径为2;
∵AG=OA,
∴∠AOG=30°,
由菱形的性质可知,∠AOG=∠COG=30°,
∴∠AOC=60°,
∴圆心角的度数为:60°;
(3)∵OD=2OG=2,
∴S菱形AOCD=AC×OD=2,
∴S扇形AOC=×π×r2=,
在菱形OBEF中,S△FHO=S△BHO,
∵S△FHO==,
∴S△FBO=2×=,
∴S阴影=S△FBO+S菱形AOCD﹣S扇形AOC=+2﹣π=3﹣.
16.【解答】解:(1)由题意,∵M(,4)在反比例函数y=上,
∴k=×4=2.
∴反比例函数表达式为y=.
又N(n,1)在反比例函数y=上,
∴n=2.
∴N(2,1).
设一次函数表达式为y=ax+b,
∴.
∴a=﹣2,b=5.
∴一次函数的表达式为y=﹣2x+5.
(2)由题意,如图,设直线l交x轴于点A,交y轴于点B,
又直线l为y=﹣2x+5,
∴A(,0),B(0,5).
∴OA=,OB=5.
∴S△OMN=S△AOB﹣S△AON﹣S△BOM=×AO×BO﹣×AO yN﹣×BO×xM
=××5﹣××1﹣×5×
=.
(3)由题意,如图,作点M关于y轴的对称点M',连接M'N交y轴于点P,则PM+PN的最小值等于M'N的长.
∵M(,4)与M'关于y轴对称,
∴M'为(﹣,4).
又N(2,1),
∴直线M′N为y=﹣x+.
令x=0,则y=,
∴P(0,).
17.【解答】解:(1)当m=3时,
又点M的横坐标为m,M在y=上,
∴M(3,1).
又MP⊥y轴,
∴P的纵坐标为1.
又∵P在y=﹣上,
∴P(﹣2,1).
∴MP=3﹣(﹣2)=5.
(2)由题意,∵点M的横坐标为m,点N的横坐标为n,M、N都在y=上,
∴M(m,),N(n,).
又MP⊥y轴,NQ⊥x轴,
∴P的纵坐标为,Q的横坐标为n.
又∵P、Q都在y=﹣上,
∴P(﹣,),Q(n,﹣).
∴MP=m﹣(﹣m)=m,NQ=﹣﹣=﹣.
又MP=NQ,
∴=﹣.
∴mn=﹣3.
(3)①由题意,根据(2)N(n,),P(﹣,),
∴△MNP的MP边上的高h为:﹣=.
又∵MP=m,
∴S△MNP=MP h=×m×=.
②相等.理由如下:
由题意,根据(2)M(m,),Q(n,﹣).
∴△MNQ的NQ边上的高h'=m﹣n.
又∵NQ=﹣,
∴S△MNQ=NQ h'=×(m﹣n)×(﹣)=.
又由①S△MNP=,
∴S△MNP=S△MNQ.
∴当MP看作底时,点P、Q到直线MN的距离相等.
18.【解答】解:(1)∵四边形OABC是矩形,
∴BC=OA,AB=OC,
∵tan∠COD=,
∴设OC=3x,CD=4x,
∴OD=5x=5,
∴x=1,
∴OC=3,CD=4,
∴D(4,3),
设过点D的反比例函数的解析式为:y=,
∴k=12,∴反比例函数的解析式为:y=;
(2)∵点D是BC的中点,
∴B(8,3),
∴BC=8,AB=3,
∵E点在过点D的反比例函数图象上,
∴E(8,),
∴S△DBE=BD BE==3;
(3)存在,
∵△OPD为直角三角形,
∴当∠OPD=90°时,PD⊥x轴于P,
∴OP=4,
∴P(4,0),
当∠ODP=90°时,
如图,过D作DH⊥x轴于H,
∴OD2=OH OP,
∴OP==.
∴P(,O),
∴存在点P使△OPD为直角三角形,
∴P(4,0),(,0).
19.【解答】解:(1)如图,连接OC,过点C作CM⊥OB于点M,
∵△OAB是正三角形,OB=4,
∴OC⊥AB,AC=BC=2,
∴OCBC=2,
在Rt△OCM中,∠COM=30°,OC=2,
∴OMOC=3,CMOC,
∴S△COMOM CM|k|,
∵k>0,
∴k=3;
(2)由中心对称图形的性质可知,∠DOF=∠AOC=30°,OD=OF=OC=2,
∴S扇形ODFπ.
20.【解答】解:(1)①根据长方形OABC中,OA=2,OC=4,
则点B坐标为(4,2),
②∵反比例函数(k>0)与长方形OABC在第一象限相交于D、E两点,
利用△OAD、△OCE的面积分别为S1AD AO,S2 CO EC,xy=k,得出,
S1AD AOk,S2 CO ECk,
∴S1=S2;
(2)当S1+S2=2时,∵S1=S2,
∴S1=S2=1,
∴k=2,
∵S1AD AOAD×2=1,
∴AD=1,
∵S2 CO EC4×EC=1,
∴EC,
∵OA=2,OC=4,
∴BD=4﹣1=3,
BE=2,
∴DO2=AO2+AD2=4+1=5,
DE2=DB2+BE2=9,
OE2=CO2+CE2=16,
∴D的坐标为(1,2),E的坐标为(4,)
∴DO2+DE2=OE2,
∴△ODE是直角三角形,
∵DO2=5,
∴DO,
∵DE2,
∴DE,
∴△ODE的面积为:DO×DE,
故答案为:(1)①(4,2);②=.
21世纪教育网(www.21cnjy.com)
同课章节目录
