复数与几何
图片预览






文档简介
课件14张PPT。复 数 与 几 何长 春 市 第 十 一 中 学李 旭由于复数与复平面上的点的一一对应关系,使复数与解析几何存在必然的联系。利用复数解曲线与方程问题成为一种有效的手段,常用的方法是两复数相等的条件的应用、复平面上两点间距离公式的使用等。在解决有关轨迹问题时,利用解析几何求轨迹的方法和复数的有关性质,使有些问题的解决更简捷。例1、已知复数z满足: ,
argz , 解: u =z+i z=u–i
由 得
z-(1+i) = z-(1+i) =
u –(1+2i)求 u=z+i 的轨迹方程。 几何意义法:
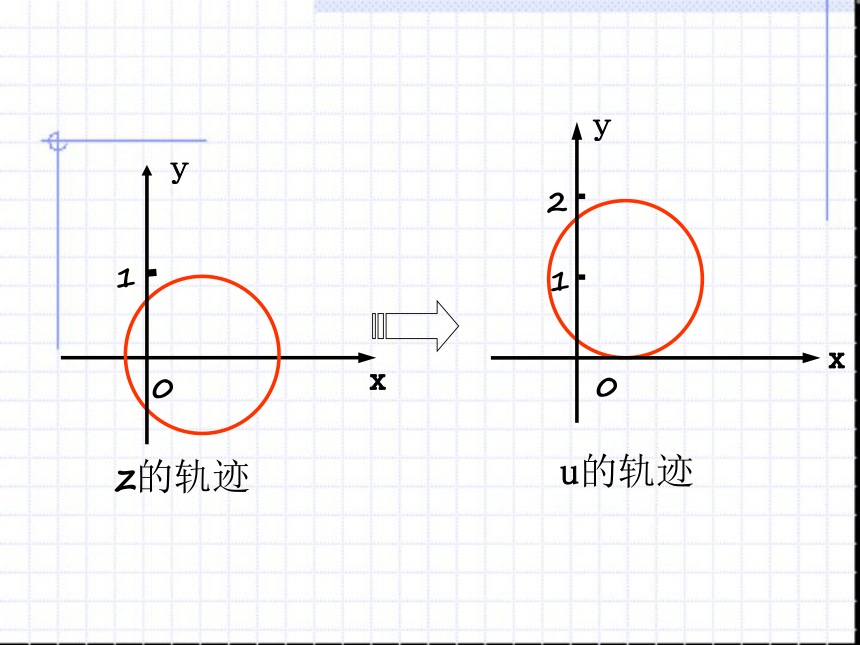
u的轨迹是由z的轨迹向上平移一个单位而得到的,
所以它的轨迹也是一个圆。
z的轨迹是一个以(1,1)为圆心, 为半径的圆,
则 u 的轨迹是以(1,2)为圆心, 为半径的圆。坐标平移的原则是什么?上加下减右减左加u的轨迹例2、B为圆x2+y2=1上的动点,A为定点(2,0),
且 ABC是以BC为斜边的等腰直角三角形,
(如图)求C点的轨迹方程。 解: 设C(x ,y),B(x’,y’)
因为zB–zA =(zC –zA)i
所以 x’ + y’ i – 2 = ( x – 2+ y i ) i
( x’ – 2 )+ i y ’ = – y + ( x + 2 ) i
x’ – 2 = – y
y’=x+2
又(x’)2+(y’)2=1
(x – 2)2+(y –2)2=1.o’例3、复数z满足不等式 , 设u=z+i,求u的辐角主角的取值范围。 又 u = z + i. 得 z = u - i解:由 已 知得即得argu例4、已知在复平面内等边三角形的两个
顶点所表示的复数为2, 。
求第三个顶点所对应的复数。 C’C分析:我们要
注意AB这条
向量的旋转
方向,可以
有两种选择。例5、已知复数z1,z2,z3满足|z1|=|z2|=|z3|,z1+z2+z3=0,求证:z1,z2,z3在复平面上对应的点A、B、C是一个内接与单位圆的正三角形的顶点。复数与几何的关系远不止上面的例子中所列举的情形,他们之间更多的联系还有待于同学们去发现和挖掘。应用复数的几何意义,解决几何中的某些问题时候,要注意变量的范围。
注意几何知识的同时使用,不一定是单纯的代数方法,注意知识的连带性。
谢谢!再见!
argz , 解: u =z+i z=u–i
由 得
z-(1+i) = z-(1+i) =
u –(1+2i)求 u=z+i 的轨迹方程。 几何意义法:
u的轨迹是由z的轨迹向上平移一个单位而得到的,
所以它的轨迹也是一个圆。
z的轨迹是一个以(1,1)为圆心, 为半径的圆,
则 u 的轨迹是以(1,2)为圆心, 为半径的圆。坐标平移的原则是什么?上加下减右减左加u的轨迹例2、B为圆x2+y2=1上的动点,A为定点(2,0),
且 ABC是以BC为斜边的等腰直角三角形,
(如图)求C点的轨迹方程。 解: 设C(x ,y),B(x’,y’)
因为zB–zA =(zC –zA)i
所以 x’ + y’ i – 2 = ( x – 2+ y i ) i
( x’ – 2 )+ i y ’ = – y + ( x + 2 ) i
x’ – 2 = – y
y’=x+2
又(x’)2+(y’)2=1
(x – 2)2+(y –2)2=1.o’例3、复数z满足不等式 , 设u=z+i,求u的辐角主角的取值范围。 又 u = z + i. 得 z = u - i解:由 已 知得即得argu例4、已知在复平面内等边三角形的两个
顶点所表示的复数为2, 。
求第三个顶点所对应的复数。 C’C分析:我们要
注意AB这条
向量的旋转
方向,可以
有两种选择。例5、已知复数z1,z2,z3满足|z1|=|z2|=|z3|,z1+z2+z3=0,求证:z1,z2,z3在复平面上对应的点A、B、C是一个内接与单位圆的正三角形的顶点。复数与几何的关系远不止上面的例子中所列举的情形,他们之间更多的联系还有待于同学们去发现和挖掘。应用复数的几何意义,解决几何中的某些问题时候,要注意变量的范围。
注意几何知识的同时使用,不一定是单纯的代数方法,注意知识的连带性。
谢谢!再见!
