苏科版2024—2025学年八年级下册数学期中考试全真模拟试卷(含答案)
文档属性
| 名称 | 苏科版2024—2025学年八年级下册数学期中考试全真模拟试卷(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 938.4KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-03-30 00:00:00 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
苏科版2024—2025学年八年级下册数学期中考试全真模拟试卷
考生注意:本试卷共三道大题,25道小题,满分120分,时量120分钟
注意事项:
1.本试卷分第I卷(选择题)和第II卷(非选择题)两部分。笞卷前,考生务必
将自己的姓名、准考证号填写在答题卡上。
2.回答第I卷时,选出每小题答案后,把答案填写在答题卡上对应题目的位置
,填空题填写在答题卡相应的位置写在本试卷上无效。
3.回答第II卷时,将答案写在第II卷答题卡上。
4.考试结束后,将本试卷和答题卡一并交回。
第I卷
一、选择题(每题只有一个正确选项,每小题3分,满分30分)
1.下列图案中,不是中心对称图形的是( )
A. B. C. D.
2.下列调查适合抽样调查的是( )
A.审核七年级上册数学书中的错别字
B.对全国中学生目前的睡眠时长进行调查
C.对乘坐飞机的乘客的安检进行调查
D.中国嫦娥六号发射之前对各部分零部件进行检测
3.一个不透明的袋子中装有2个红球、3个白球,每个球除颜色外都相同.从中任意摸出3个球,下列事件为必然事件的是( )
A.至少有1个球是红球 B.至少有1个球是白球
C.至少有2个球是红球 D.至少有2个球是白球
4.如图,小义同学想测量池塘A,B两处之间的距离.他先在A,B外选一点C,然后步测AC,BC的中点为D,E,测得DE=20m,则A,B之间的距离为( )
A.10m B.20m C.30m D.40m
5.如图,在 ABCD中,E是BC边上一点,BE=CD,连接AE,∠D=50°,则∠DAE的度数为( )
A.65° B.60° C.55° D.50°
6.一只不透明的袋中装有除颜色外都相同的红球、黄球、白球共50个.通过多次摸球试验后,发现摸到红球、黄球的频率分别是0.2、0.4.则可估计袋中白球的个数是( )
A.10 B.15 C.25 D.20
7.把分式中的x和y都扩大3倍,分式的值( )
A.不变 B.扩大3倍 C.缩小3倍 D.扩大9倍
8.如图,在四边形ABCD中,E、F、G、H分别是边AB、BC、CD、DA、的中点.请你添加一个条件,使四边形EFGH为菱形,应添加的条件是( )
A.AB=CD B.AC⊥BD C.CD=BC D.AC=BD
9.已知关于x的分式方程的解为非负数,则a的取值范围是( )
A.a≤2 B.a<2 C.a≤2且a≠﹣4 D.a<2且a≠﹣4
10.如图,在正方形OABC中,点B的坐标是(4,4),点E、F分别在边BC、BA上,OE=2.若∠EOF=45°,则F点的纵坐标是( )
A.1 B. C. D.1
二、填空题(6小题,每题3分,共18分)
11.在分式中,当x= 时,分式的值为零.
12.当2时,的值是 .
13.从某玉米种子中抽取6批,在同一条件下进行发芽试验,有关数据如下:
种子粒数 100 400 800 1000 2000 5000
发芽种子粒数 85 298 652 793 1604 4005
发芽频率 0.850 0.745 0.815 0.793 0.802 0.801
根据以上数据可以估计,该玉米种子发芽的概率约为 (精确到0.1).
14.如图,在矩形纸片ABCD中,AB=3,BC=4,将矩形纸片折叠,使点B与点D重合,则折痕EF的长为 .
15.如图,在菱形ABCD中,P是对角线AC上一动点,过点P作PE⊥BC于点E,PF⊥AB于点F.若菱形ABCD的周长为20,面积为24,则PE+PF的值为 .
16.如图,将边长为2的正方形ABCD纸片沿EF折叠,点C落在AB边上的点G处,点D与点H重合,CG与EF交于点P,取GH的中点Q,连接PQ,则△GPQ周长的最小值是 .
第II卷
苏科版2024—2025学年八年级下册数学期中考试全真模拟试卷
姓名:____________ 学号:____________准考证号:___________
一、选择题
题号 1 2 3 4 5 6 7 8 9 10
答案
二、填空题
11、_______ 12、______13、_______ 14、______15、_______ 16、______
三、解答题解答题(17、18、19题每题6分,20、21每题8分,22、23每题9分,24、25每题10分,共计72分,解答题要有必要的文字说明)
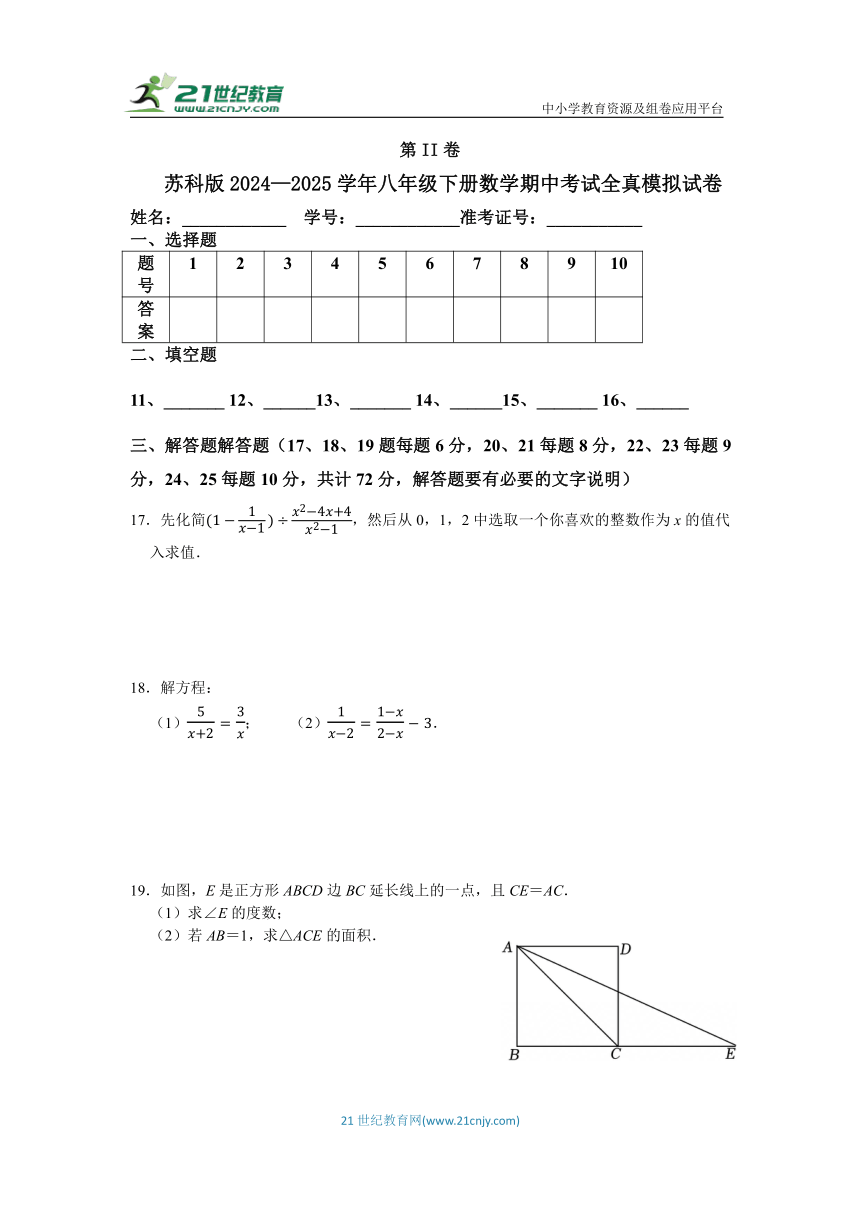
17.先化简,然后从0,1,2中选取一个你喜欢的整数作为x的值代入求值.
18.解方程:
(1); (2).
19.如图,E是正方形ABCD边BC延长线上的一点,且CE=AC.
(1)求∠E的度数;
(2)若AB=1,求△ACE的面积.
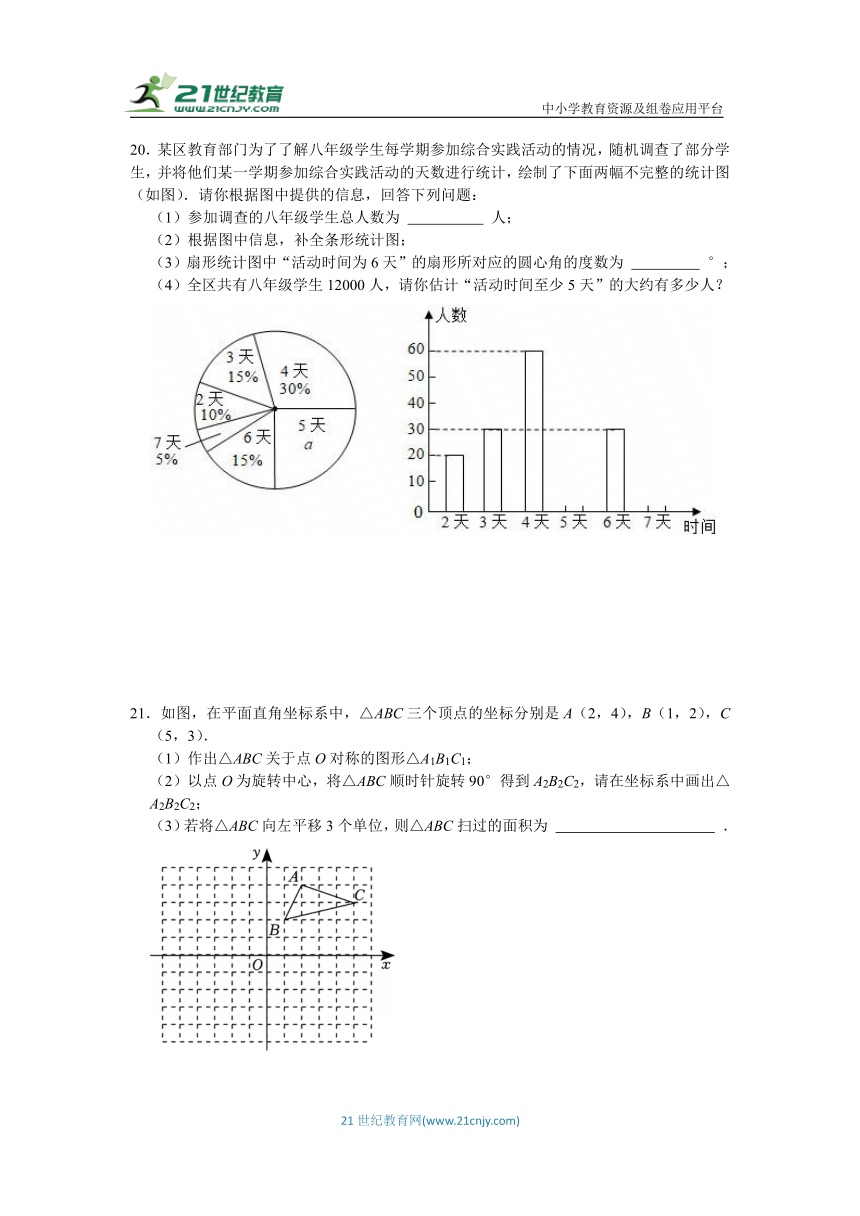
20.某区教育部门为了了解八年级学生每学期参加综合实践活动的情况,随机调查了部分学生,并将他们某一学期参加综合实践活动的天数进行统计,绘制了下面两幅不完整的统计图(如图).请你根据图中提供的信息,回答下列问题:
(1)参加调查的八年级学生总人数为 人;
(2)根据图中信息,补全条形统计图;
(3)扇形统计图中“活动时间为6天”的扇形所对应的圆心角的度数为 °;
(4)全区共有八年级学生12000人,请你估计“活动时间至少5天”的大约有多少人?
21.如图,在平面直角坐标系中,△ABC三个顶点的坐标分别是A(2,4),B(1,2),C(5,3).
(1)作出△ABC关于点O对称的图形△A1B1C1;
(2)以点O为旋转中心,将△ABC顺时针旋转90°得到A2B2C2,请在坐标系中画出△A2B2C2;
(3)若将△ABC向左平移3个单位,则△ABC扫过的面积为 .
22.佳佳果品店在批发市场购买某种水果销售,第一次用1200元购进若干千克,很快售完.由于水果畅销,第二次购买时,每千克的进价比第一次提高了10%,用1452元所购买的数量比第一次多20千克.
(1)求第一次水果的进价是每千克多少元?
(2)若第一次购进的水果以每千克8元出售,很快售完.第二次购进的水果以每千克9元售出100千克后,因出现高温天气,水果不易保鲜,为减少损失,便降价50%售完剩余的水果.该果品店在这两次销售中,总体上是盈利还是亏损?盈利或亏损了多少元?
23.如图,在四边形ABCD中,AB∥DC,AB=AD,对角线AC,BD交于点O,AC平分∠BAD,过点C作CE⊥AB交AB的延长线于点E.
(1)求证:四边形ABCD是菱形;
(2)若,BD=2,求BE的长.
24.如图1,在△ABC中,∠ACB=90°.以AC边、AB边向外分别作正方形ACDE、正方形ABGF.
(1)连接BE,CF,求证:△EAB≌△CAF;
(2)连接EF,若AC=9,AB=15,求S△EAF:S△EAB的值;
(3)若点P是BC中点,连接PA并延长交EF为点Q,求证:PQ⊥EF.
25.在矩形ABCD中,AB=6,BC=12,点E是矩形ABCD边CD上一点,连接BE,将△CEB沿BE翻折,
(1)如图1,点C刚好落在边AD上的点F处,求AF长.
(2)如图2,点C落在矩形外一点F处,连接AF,若CE=4,求△ABF的面积.
(3)如图3,点C落在点F处,∠ABF的角平分线与EF的延长线交于点M,当点E从点C运动到点D时,求点M运动的路径长.
参考答案
一、选择题
题号 1 2 3 4 5 6 7 8 9 10
答案 B B B D A D B D C B
1.【解答】解:选项A、C、D都能找到一个点,使图形绕某一点旋转180度后与原来的图形重合,所以是中心对称图形.
选项B不能找到一个点,使图形绕某一点旋转180度后与原来的图形重合,所以不是中心对称图形.
故选:B.
2.【解答】解:A、审核北师大版七年级上册数学书中的错别字,适合全面调查,不符合题意;
B、对全国中学生目前的睡眠时长进行调查,适合抽样调查,符合题意;
C、对乘坐飞机的乘客的安检进行调查,适合全面调查,不符合题意;
D、中国嫦娥六号发射之前对各部分零部件进行检测,适合全面调查,不符合题意;
故选:B.
3.【解答】解:A、至少有1个球是红球是随机事件,选项错误;
B、至少有1个球是白球是必然事件,选项正确;
C、至少有2个球是红球是随机事件,选项错误;
D、至少有2个球是白球是随机事件,选项错误.
故选:B.
4.【解答】解:∵AC,BC的中点为D,E,测得DE=20m,
∴DE是三角形ABC的中位线,
∴,
∵DE=20m,
∴AB=2DE=2×20=40(m).
故选:D.
5.【解答】解:在 ABCD中,AB=CD,∠B=∠D=50°.
∵AB=CD,BE=CD,
∴AB=BE.
∴∠BAE=∠BEA=65°,
∵AD∥BC,
∴∠DAE=65°,
故选:A.
6.【解答】解:∵通过多次摸球试验后,发现摸到红球、黄球的频率分别是0.2、0.4.
∴估计摸到白球的频率为1﹣0.2﹣0.4=0.4,
∴可估计袋中白球的个数是50×0.4=20(个).
故选:D.
7.【解答】解:分别用3x和3y去代换原分式中的x和y,得
3,
故选:B.
8.【解答】解:应添加的条件是AC=BD,理由为:
证明:∵E、F、G、H分别为AB、BC、CD、DA的中点,且AC=BD,
∴EHBD,FGBD,HGAC,EFAC,
∴EH=HG=GF=EF,
则四边形EFGH为菱形,
故选:D.
9.【解答】解:分式方程去分母得:2x+a=﹣x+2,
移项合并得:3x=2﹣a,
解得:x,
∵分式方程的解为非负数,
∴0,且2,
解得:a≤2,且a≠﹣4.
故选:C.
10.【解答】解:如图,连接EF,延长BA,使得AM=CE,
∵OA=OC,∠OCE=∠AOM,
∴△OCE≌△OAM(SAS).
∴OE=OM,∠COE=∠MOA,
∵∠EOF=45°,
∴∠COE+∠AOF=45°,
∴∠MOA+∠AOF=45°,
∴∠EOF=∠MOF,
在△OFE和△OFM中,
,
∴△OFE≌△OFM(SAS),
∴EF=FM=AF+AM=AF+CE,设AF=x,
∵CE2,
∴EF=2+x,EB=2,FB=4﹣x,
∴(2+x)2=22+(4﹣x)2,
∴x,
∴点F的纵坐标为,
故选:B.
二、填空题
11.【解答】解:由题意得:x2﹣1=0且x﹣1≠0,
解得:x=﹣1.
故答案为:﹣1.
12.【解答】解:当2时,
,
故的值是.
故答案为.
13.【解答】解:∵种子粒数5000粒时,种子发芽的频率趋近于0.801,
∴估计种子发芽的概率为0.801,精确到0.1,即为0.8.
故本题答案为:0.8.
14.【解答】解:连接BD,BE,DF,
由翻折可得,EF垂直且平分BD,BF=DF,BE=DE,∠BFE=∠DFE,
∵四边形ABCD为矩形,
∴AB=CD=3,∠C=90°,AD∥BC,
∴∠DEF=∠BFE,
∴∠DEF=∠DFE,
即DE=DF,
∴DE=BE=BF=DF,
则四边形BEDF为菱形.
在Rt△BCD中,
BD5,
设BF=x,则CF=BC﹣BF=4﹣x,
在Rt△CDF中,由勾股定理可得,
x2=(4﹣x)2+32,
解得x,
∵,
即,
∴,
解得EF.
故答案为:.
15.【解答】解:连接BP,如图,
∵四边形ABCD为菱形,菱形ABCD的周长为20,
∴BA=BC=5,S△ABCS菱形ABCD=12,
∵S△ABC=S△PAB+S△PBC,
∴5×PE5×PF=12,
∴PE+PF,
故答案为:.
16.【解答】解:如图,取CD的中点N,连接PN,PB,BN,
由翻折的性质以及对称性可知;PQ=PN,PG=PC,GH=CD=2,
∵点Q是GH的中点,
∴,
在Rt△BCN中,,
∵∠CBG=90°,PC=PG,
∴PB=PG=PC,
∴,
∴PQ+PG的最小值为,
∴△GPQ的周长的最小值为,
故答案为:.
三、解答题
17.【解答】解:原式
,
∵x﹣1≠0且x+1≠0且x﹣2≠0,
∴x可以取0,
当x=0时,原式.
18.【解答】解:(1),
去分母得:5x=3(x+2),
解得:x=3,
检验:当x=3时,x(x+2)≠0,
所以原方程的解为x=3;
(2),
去分母得:1=x﹣1﹣3(x﹣2),
解得:x=2,
检验:当x=2时x﹣2=0,
所以x=2是增根,原方程无解.
19.【解答】解:(1)∵四边形ABCD为正方形,
∴,
∴∠ACE=180°﹣45°=135°,
∵CE=AC,
∴.
(2)∵四边形ABCD为正方形,
∴AB=BC=CD=AD=1,∠B=90°,
∴,
∴,
∴.
20.【解答】解:(1)参加调查的八年级学生总人数为:20÷10%=200(人);
故答案为:200;
(2)实践活动7天的人数有:200×5%=10(人),
实践活动5天的人数有:200﹣20﹣30﹣60﹣30﹣10=50(人),
补全统计图如下:
(3)“活动时间为6天”的扇形所对应的圆心角的度数是:360°×15%=54°;
故答案为:54;
(4)根据题意得:120005400(人),
答:估计“活动时间至少5天”的大约有5400人.
21.【解答】解:(1)如图,△A1B1C1即为所求作;
(2)如图,△A2B2C2即为所求作;
(3)△ABC扫过的面积=2×71×31×41×2.
22.【解答】解:(1)设第一次购买的单价为x元,则第二次的单价为1.1x元,
根据题意得:20,
解得:x=6,
经检验,x=6是原方程的解,
(2)第一次购水果1200÷6=200(千克).
第二次购水果200+20=220(千克).
第一次赚钱为200×(8﹣6)=400(元).
第二次赚钱为100×(9﹣6.6)+120×(9×0.5﹣6×1.1)=﹣12(元).
所以两次共赚钱400﹣12=388(元),
答:第一次水果的进价为每千克6元,该老板两次卖水果总体上是赚钱了,共赚了388元.
23.【解答】(1)证明:∵AB∥DC,
∴∠OAB=∠DCA,
∵AC平分∠DAB,
∴∠OAB=∠DAC,
∴∠DCA=∠DAC,则AD=CD,
又∵AB=AD,
∴CD=AD=AB,
∵AB∥CD,
∴四边形ABCD是平行四边形,
∵AB=AD,
∴四边形ABCD是菱形.
(2)解:∵四边形ABCD是菱形,
∴,BD⊥AC,,,
由勾股定理可得:,
∵CE⊥AB,
在Rt△BCE中,CE2=BC2﹣BE2,
在Rt△ACE中,CE2=AC2﹣AE2=AC2﹣(AB+BE)2,
∴BC2﹣BE2=AC2﹣(AB+BE)2,即:,
解得:.
24.【解答】(1)证明:∵四边形ACDE,ABGF为正方形,
∴EA=CA,AB=AF,∠EAC=∠FAB=90°,
∴∠EAC+∠CAB=∠FAB+∠CAB,
即∠EAB=∠CAF,
在△EAB和△CAF中,
,
∴△EAB≌△CAF(SAS);
(2)解:在Rt△ACB中,AC=9,AB=15,
∴,
分别过点B、F作直线AE的垂线BM、FN,垂足分别为M、N,
∴∠ANF=∠AMB=∠FAB=∠ACB=90°,
∴∠1+∠2=∠3+∠2=90°,
∴∠1=∠3,
∵CA⊥EA,BM⊥EA,
∴CA∥BM,
∴∠3=∠BAC=∠1,
在正方形AFGB中,AF=AB,
∴△AFN≌△BAM≌△ABC(AAS),
∴FN=CB=12,BM=AC=9,
∵S△EAFAE×FN,S△EABAE×BM,
∴S△EAF:S△EAB=FN:BM;
(3)如图,延长AP至点H,使得PH=PA,连接BH,
∵P是BC中点,
∴CP=PB,
又∠CPA=∠BPH,
∴△ACP≌△HBP(SAS),
∴HB=CA,∠HBC=∠ACB=90°,
设∠ABC=α,∠CAB=90°﹣α,
∴∠EAF=360°﹣∠EAC﹣∠CAB﹣∠BAF=90°+α,
∵∠HBA=∠HBC+∠CBA=90°+α,
∴∠EAF=∠HBA,
在△ABH和△FAE中,
,
∴△ABH≌△FAE(SAS),
∴∠HAB=∠EFA,
∵∠HAB+∠QAF=90°,
∴∠EFA+∠QAF=90°,即∠FQA=90°,
∴EF⊥PQ,
25.【解答】解:(1)由题意得:△BCE≌△BFE,
∴∠BFE=∠C=90°,BC=BF=12,
∵四边形ABCD为矩形,
∴∠A=90°,
∴AF6.
(2)过点F作FG⊥AB,交AB的延长线于点G,延长GF交CD的延长线于点H,如图,
∵四边形ABCD为矩形,
∴AB⊥AB,AB⊥BC,CD⊥BC,CD⊥AD,
∵FG⊥AB,
∴四边形BCHG,四边形ADHG为矩形,
∴GH=AD=BC=12,AG=HD,BG=CH,
设HD=AG=x,则HE=x+2,BG=x+6,
由题意得:△BCE≌△BFE,
∴∠BFE=∠C=90°,BC=BF=12,FE=CE=4.
∴∠EFH+∠GFB=90°.
∵∠GFB+∠GBF=90°,
∴∠EFH=∠GBF.
∵∠H=∠G=90°,
∴GF=3EH=3x+6,FHBGx+2,
∵GH=12,
∴3x+6x+2=12,
∴x.
∴FG=36,
∴△ABF的面积AB FG.
(3)过点M作MG⊥AB,交AB的延长线于点G,延长GM交CD的延长线于点H,如图
∵四边形ABCD为矩形,
∴AB⊥AB,AB⊥BC,CD⊥BC,CD⊥AD,
∵MG⊥AB,
∴四边形BCHG,四边形ADHG为矩形,
∴GH=AD=BC=12,AG=HD,BG=CH,
由题意得:△BCE≌△BFE,
∴∠BFE=∠C=90°,BC=BF=12,
∴∠G=∠BFM=90°.
∵BM为∠GBF的平分线,
∴∠GBM=∠FBM.
在△BGM和△BFM中,
,
∴△BGM≌△BFM(AAS),
∴BG=BF=12,
∴AG=BG=AB=6,
∵点M在GH上,
∴点M到AD的距离等于AG=6,即点M在GH上运动,
∴点E与点C重合时,点M与点H重合.
当点E与点D重合时,如图,
∵△BGM≌△BFM,
∴MG=MF,
由题意得:△BCE≌△BFE,
∴CD=DF=6.
∵四边形ADHG为矩形,
∴DH=AG=6.
设MG=MF=x,则MD=x+6,MH=GH﹣GM=12﹣x.
∵∠H=90°,
∴MD2=MH2+DH2,
∴(x+6)2=(12﹣x)2+62.
∴x=4.
∴MH=GH﹣GM=8.
∴当点E从点C运动到点D时,点M运动的路径长为线段HM的长等于8.
21世纪教育网(www.21cnjy.com)
苏科版2024—2025学年八年级下册数学期中考试全真模拟试卷
考生注意:本试卷共三道大题,25道小题,满分120分,时量120分钟
注意事项:
1.本试卷分第I卷(选择题)和第II卷(非选择题)两部分。笞卷前,考生务必
将自己的姓名、准考证号填写在答题卡上。
2.回答第I卷时,选出每小题答案后,把答案填写在答题卡上对应题目的位置
,填空题填写在答题卡相应的位置写在本试卷上无效。
3.回答第II卷时,将答案写在第II卷答题卡上。
4.考试结束后,将本试卷和答题卡一并交回。
第I卷
一、选择题(每题只有一个正确选项,每小题3分,满分30分)
1.下列图案中,不是中心对称图形的是( )
A. B. C. D.
2.下列调查适合抽样调查的是( )
A.审核七年级上册数学书中的错别字
B.对全国中学生目前的睡眠时长进行调查
C.对乘坐飞机的乘客的安检进行调查
D.中国嫦娥六号发射之前对各部分零部件进行检测
3.一个不透明的袋子中装有2个红球、3个白球,每个球除颜色外都相同.从中任意摸出3个球,下列事件为必然事件的是( )
A.至少有1个球是红球 B.至少有1个球是白球
C.至少有2个球是红球 D.至少有2个球是白球
4.如图,小义同学想测量池塘A,B两处之间的距离.他先在A,B外选一点C,然后步测AC,BC的中点为D,E,测得DE=20m,则A,B之间的距离为( )
A.10m B.20m C.30m D.40m
5.如图,在 ABCD中,E是BC边上一点,BE=CD,连接AE,∠D=50°,则∠DAE的度数为( )
A.65° B.60° C.55° D.50°
6.一只不透明的袋中装有除颜色外都相同的红球、黄球、白球共50个.通过多次摸球试验后,发现摸到红球、黄球的频率分别是0.2、0.4.则可估计袋中白球的个数是( )
A.10 B.15 C.25 D.20
7.把分式中的x和y都扩大3倍,分式的值( )
A.不变 B.扩大3倍 C.缩小3倍 D.扩大9倍
8.如图,在四边形ABCD中,E、F、G、H分别是边AB、BC、CD、DA、的中点.请你添加一个条件,使四边形EFGH为菱形,应添加的条件是( )
A.AB=CD B.AC⊥BD C.CD=BC D.AC=BD
9.已知关于x的分式方程的解为非负数,则a的取值范围是( )
A.a≤2 B.a<2 C.a≤2且a≠﹣4 D.a<2且a≠﹣4
10.如图,在正方形OABC中,点B的坐标是(4,4),点E、F分别在边BC、BA上,OE=2.若∠EOF=45°,则F点的纵坐标是( )
A.1 B. C. D.1
二、填空题(6小题,每题3分,共18分)
11.在分式中,当x= 时,分式的值为零.
12.当2时,的值是 .
13.从某玉米种子中抽取6批,在同一条件下进行发芽试验,有关数据如下:
种子粒数 100 400 800 1000 2000 5000
发芽种子粒数 85 298 652 793 1604 4005
发芽频率 0.850 0.745 0.815 0.793 0.802 0.801
根据以上数据可以估计,该玉米种子发芽的概率约为 (精确到0.1).
14.如图,在矩形纸片ABCD中,AB=3,BC=4,将矩形纸片折叠,使点B与点D重合,则折痕EF的长为 .
15.如图,在菱形ABCD中,P是对角线AC上一动点,过点P作PE⊥BC于点E,PF⊥AB于点F.若菱形ABCD的周长为20,面积为24,则PE+PF的值为 .
16.如图,将边长为2的正方形ABCD纸片沿EF折叠,点C落在AB边上的点G处,点D与点H重合,CG与EF交于点P,取GH的中点Q,连接PQ,则△GPQ周长的最小值是 .
第II卷
苏科版2024—2025学年八年级下册数学期中考试全真模拟试卷
姓名:____________ 学号:____________准考证号:___________
一、选择题
题号 1 2 3 4 5 6 7 8 9 10
答案
二、填空题
11、_______ 12、______13、_______ 14、______15、_______ 16、______
三、解答题解答题(17、18、19题每题6分,20、21每题8分,22、23每题9分,24、25每题10分,共计72分,解答题要有必要的文字说明)
17.先化简,然后从0,1,2中选取一个你喜欢的整数作为x的值代入求值.
18.解方程:
(1); (2).
19.如图,E是正方形ABCD边BC延长线上的一点,且CE=AC.
(1)求∠E的度数;
(2)若AB=1,求△ACE的面积.
20.某区教育部门为了了解八年级学生每学期参加综合实践活动的情况,随机调查了部分学生,并将他们某一学期参加综合实践活动的天数进行统计,绘制了下面两幅不完整的统计图(如图).请你根据图中提供的信息,回答下列问题:
(1)参加调查的八年级学生总人数为 人;
(2)根据图中信息,补全条形统计图;
(3)扇形统计图中“活动时间为6天”的扇形所对应的圆心角的度数为 °;
(4)全区共有八年级学生12000人,请你估计“活动时间至少5天”的大约有多少人?
21.如图,在平面直角坐标系中,△ABC三个顶点的坐标分别是A(2,4),B(1,2),C(5,3).
(1)作出△ABC关于点O对称的图形△A1B1C1;
(2)以点O为旋转中心,将△ABC顺时针旋转90°得到A2B2C2,请在坐标系中画出△A2B2C2;
(3)若将△ABC向左平移3个单位,则△ABC扫过的面积为 .
22.佳佳果品店在批发市场购买某种水果销售,第一次用1200元购进若干千克,很快售完.由于水果畅销,第二次购买时,每千克的进价比第一次提高了10%,用1452元所购买的数量比第一次多20千克.
(1)求第一次水果的进价是每千克多少元?
(2)若第一次购进的水果以每千克8元出售,很快售完.第二次购进的水果以每千克9元售出100千克后,因出现高温天气,水果不易保鲜,为减少损失,便降价50%售完剩余的水果.该果品店在这两次销售中,总体上是盈利还是亏损?盈利或亏损了多少元?
23.如图,在四边形ABCD中,AB∥DC,AB=AD,对角线AC,BD交于点O,AC平分∠BAD,过点C作CE⊥AB交AB的延长线于点E.
(1)求证:四边形ABCD是菱形;
(2)若,BD=2,求BE的长.
24.如图1,在△ABC中,∠ACB=90°.以AC边、AB边向外分别作正方形ACDE、正方形ABGF.
(1)连接BE,CF,求证:△EAB≌△CAF;
(2)连接EF,若AC=9,AB=15,求S△EAF:S△EAB的值;
(3)若点P是BC中点,连接PA并延长交EF为点Q,求证:PQ⊥EF.
25.在矩形ABCD中,AB=6,BC=12,点E是矩形ABCD边CD上一点,连接BE,将△CEB沿BE翻折,
(1)如图1,点C刚好落在边AD上的点F处,求AF长.
(2)如图2,点C落在矩形外一点F处,连接AF,若CE=4,求△ABF的面积.
(3)如图3,点C落在点F处,∠ABF的角平分线与EF的延长线交于点M,当点E从点C运动到点D时,求点M运动的路径长.
参考答案
一、选择题
题号 1 2 3 4 5 6 7 8 9 10
答案 B B B D A D B D C B
1.【解答】解:选项A、C、D都能找到一个点,使图形绕某一点旋转180度后与原来的图形重合,所以是中心对称图形.
选项B不能找到一个点,使图形绕某一点旋转180度后与原来的图形重合,所以不是中心对称图形.
故选:B.
2.【解答】解:A、审核北师大版七年级上册数学书中的错别字,适合全面调查,不符合题意;
B、对全国中学生目前的睡眠时长进行调查,适合抽样调查,符合题意;
C、对乘坐飞机的乘客的安检进行调查,适合全面调查,不符合题意;
D、中国嫦娥六号发射之前对各部分零部件进行检测,适合全面调查,不符合题意;
故选:B.
3.【解答】解:A、至少有1个球是红球是随机事件,选项错误;
B、至少有1个球是白球是必然事件,选项正确;
C、至少有2个球是红球是随机事件,选项错误;
D、至少有2个球是白球是随机事件,选项错误.
故选:B.
4.【解答】解:∵AC,BC的中点为D,E,测得DE=20m,
∴DE是三角形ABC的中位线,
∴,
∵DE=20m,
∴AB=2DE=2×20=40(m).
故选:D.
5.【解答】解:在 ABCD中,AB=CD,∠B=∠D=50°.
∵AB=CD,BE=CD,
∴AB=BE.
∴∠BAE=∠BEA=65°,
∵AD∥BC,
∴∠DAE=65°,
故选:A.
6.【解答】解:∵通过多次摸球试验后,发现摸到红球、黄球的频率分别是0.2、0.4.
∴估计摸到白球的频率为1﹣0.2﹣0.4=0.4,
∴可估计袋中白球的个数是50×0.4=20(个).
故选:D.
7.【解答】解:分别用3x和3y去代换原分式中的x和y,得
3,
故选:B.
8.【解答】解:应添加的条件是AC=BD,理由为:
证明:∵E、F、G、H分别为AB、BC、CD、DA的中点,且AC=BD,
∴EHBD,FGBD,HGAC,EFAC,
∴EH=HG=GF=EF,
则四边形EFGH为菱形,
故选:D.
9.【解答】解:分式方程去分母得:2x+a=﹣x+2,
移项合并得:3x=2﹣a,
解得:x,
∵分式方程的解为非负数,
∴0,且2,
解得:a≤2,且a≠﹣4.
故选:C.
10.【解答】解:如图,连接EF,延长BA,使得AM=CE,
∵OA=OC,∠OCE=∠AOM,
∴△OCE≌△OAM(SAS).
∴OE=OM,∠COE=∠MOA,
∵∠EOF=45°,
∴∠COE+∠AOF=45°,
∴∠MOA+∠AOF=45°,
∴∠EOF=∠MOF,
在△OFE和△OFM中,
,
∴△OFE≌△OFM(SAS),
∴EF=FM=AF+AM=AF+CE,设AF=x,
∵CE2,
∴EF=2+x,EB=2,FB=4﹣x,
∴(2+x)2=22+(4﹣x)2,
∴x,
∴点F的纵坐标为,
故选:B.
二、填空题
11.【解答】解:由题意得:x2﹣1=0且x﹣1≠0,
解得:x=﹣1.
故答案为:﹣1.
12.【解答】解:当2时,
,
故的值是.
故答案为.
13.【解答】解:∵种子粒数5000粒时,种子发芽的频率趋近于0.801,
∴估计种子发芽的概率为0.801,精确到0.1,即为0.8.
故本题答案为:0.8.
14.【解答】解:连接BD,BE,DF,
由翻折可得,EF垂直且平分BD,BF=DF,BE=DE,∠BFE=∠DFE,
∵四边形ABCD为矩形,
∴AB=CD=3,∠C=90°,AD∥BC,
∴∠DEF=∠BFE,
∴∠DEF=∠DFE,
即DE=DF,
∴DE=BE=BF=DF,
则四边形BEDF为菱形.
在Rt△BCD中,
BD5,
设BF=x,则CF=BC﹣BF=4﹣x,
在Rt△CDF中,由勾股定理可得,
x2=(4﹣x)2+32,
解得x,
∵,
即,
∴,
解得EF.
故答案为:.
15.【解答】解:连接BP,如图,
∵四边形ABCD为菱形,菱形ABCD的周长为20,
∴BA=BC=5,S△ABCS菱形ABCD=12,
∵S△ABC=S△PAB+S△PBC,
∴5×PE5×PF=12,
∴PE+PF,
故答案为:.
16.【解答】解:如图,取CD的中点N,连接PN,PB,BN,
由翻折的性质以及对称性可知;PQ=PN,PG=PC,GH=CD=2,
∵点Q是GH的中点,
∴,
在Rt△BCN中,,
∵∠CBG=90°,PC=PG,
∴PB=PG=PC,
∴,
∴PQ+PG的最小值为,
∴△GPQ的周长的最小值为,
故答案为:.
三、解答题
17.【解答】解:原式
,
∵x﹣1≠0且x+1≠0且x﹣2≠0,
∴x可以取0,
当x=0时,原式.
18.【解答】解:(1),
去分母得:5x=3(x+2),
解得:x=3,
检验:当x=3时,x(x+2)≠0,
所以原方程的解为x=3;
(2),
去分母得:1=x﹣1﹣3(x﹣2),
解得:x=2,
检验:当x=2时x﹣2=0,
所以x=2是增根,原方程无解.
19.【解答】解:(1)∵四边形ABCD为正方形,
∴,
∴∠ACE=180°﹣45°=135°,
∵CE=AC,
∴.
(2)∵四边形ABCD为正方形,
∴AB=BC=CD=AD=1,∠B=90°,
∴,
∴,
∴.
20.【解答】解:(1)参加调查的八年级学生总人数为:20÷10%=200(人);
故答案为:200;
(2)实践活动7天的人数有:200×5%=10(人),
实践活动5天的人数有:200﹣20﹣30﹣60﹣30﹣10=50(人),
补全统计图如下:
(3)“活动时间为6天”的扇形所对应的圆心角的度数是:360°×15%=54°;
故答案为:54;
(4)根据题意得:120005400(人),
答:估计“活动时间至少5天”的大约有5400人.
21.【解答】解:(1)如图,△A1B1C1即为所求作;
(2)如图,△A2B2C2即为所求作;
(3)△ABC扫过的面积=2×71×31×41×2.
22.【解答】解:(1)设第一次购买的单价为x元,则第二次的单价为1.1x元,
根据题意得:20,
解得:x=6,
经检验,x=6是原方程的解,
(2)第一次购水果1200÷6=200(千克).
第二次购水果200+20=220(千克).
第一次赚钱为200×(8﹣6)=400(元).
第二次赚钱为100×(9﹣6.6)+120×(9×0.5﹣6×1.1)=﹣12(元).
所以两次共赚钱400﹣12=388(元),
答:第一次水果的进价为每千克6元,该老板两次卖水果总体上是赚钱了,共赚了388元.
23.【解答】(1)证明:∵AB∥DC,
∴∠OAB=∠DCA,
∵AC平分∠DAB,
∴∠OAB=∠DAC,
∴∠DCA=∠DAC,则AD=CD,
又∵AB=AD,
∴CD=AD=AB,
∵AB∥CD,
∴四边形ABCD是平行四边形,
∵AB=AD,
∴四边形ABCD是菱形.
(2)解:∵四边形ABCD是菱形,
∴,BD⊥AC,,,
由勾股定理可得:,
∵CE⊥AB,
在Rt△BCE中,CE2=BC2﹣BE2,
在Rt△ACE中,CE2=AC2﹣AE2=AC2﹣(AB+BE)2,
∴BC2﹣BE2=AC2﹣(AB+BE)2,即:,
解得:.
24.【解答】(1)证明:∵四边形ACDE,ABGF为正方形,
∴EA=CA,AB=AF,∠EAC=∠FAB=90°,
∴∠EAC+∠CAB=∠FAB+∠CAB,
即∠EAB=∠CAF,
在△EAB和△CAF中,
,
∴△EAB≌△CAF(SAS);
(2)解:在Rt△ACB中,AC=9,AB=15,
∴,
分别过点B、F作直线AE的垂线BM、FN,垂足分别为M、N,
∴∠ANF=∠AMB=∠FAB=∠ACB=90°,
∴∠1+∠2=∠3+∠2=90°,
∴∠1=∠3,
∵CA⊥EA,BM⊥EA,
∴CA∥BM,
∴∠3=∠BAC=∠1,
在正方形AFGB中,AF=AB,
∴△AFN≌△BAM≌△ABC(AAS),
∴FN=CB=12,BM=AC=9,
∵S△EAFAE×FN,S△EABAE×BM,
∴S△EAF:S△EAB=FN:BM;
(3)如图,延长AP至点H,使得PH=PA,连接BH,
∵P是BC中点,
∴CP=PB,
又∠CPA=∠BPH,
∴△ACP≌△HBP(SAS),
∴HB=CA,∠HBC=∠ACB=90°,
设∠ABC=α,∠CAB=90°﹣α,
∴∠EAF=360°﹣∠EAC﹣∠CAB﹣∠BAF=90°+α,
∵∠HBA=∠HBC+∠CBA=90°+α,
∴∠EAF=∠HBA,
在△ABH和△FAE中,
,
∴△ABH≌△FAE(SAS),
∴∠HAB=∠EFA,
∵∠HAB+∠QAF=90°,
∴∠EFA+∠QAF=90°,即∠FQA=90°,
∴EF⊥PQ,
25.【解答】解:(1)由题意得:△BCE≌△BFE,
∴∠BFE=∠C=90°,BC=BF=12,
∵四边形ABCD为矩形,
∴∠A=90°,
∴AF6.
(2)过点F作FG⊥AB,交AB的延长线于点G,延长GF交CD的延长线于点H,如图,
∵四边形ABCD为矩形,
∴AB⊥AB,AB⊥BC,CD⊥BC,CD⊥AD,
∵FG⊥AB,
∴四边形BCHG,四边形ADHG为矩形,
∴GH=AD=BC=12,AG=HD,BG=CH,
设HD=AG=x,则HE=x+2,BG=x+6,
由题意得:△BCE≌△BFE,
∴∠BFE=∠C=90°,BC=BF=12,FE=CE=4.
∴∠EFH+∠GFB=90°.
∵∠GFB+∠GBF=90°,
∴∠EFH=∠GBF.
∵∠H=∠G=90°,
∴GF=3EH=3x+6,FHBGx+2,
∵GH=12,
∴3x+6x+2=12,
∴x.
∴FG=36,
∴△ABF的面积AB FG.
(3)过点M作MG⊥AB,交AB的延长线于点G,延长GM交CD的延长线于点H,如图
∵四边形ABCD为矩形,
∴AB⊥AB,AB⊥BC,CD⊥BC,CD⊥AD,
∵MG⊥AB,
∴四边形BCHG,四边形ADHG为矩形,
∴GH=AD=BC=12,AG=HD,BG=CH,
由题意得:△BCE≌△BFE,
∴∠BFE=∠C=90°,BC=BF=12,
∴∠G=∠BFM=90°.
∵BM为∠GBF的平分线,
∴∠GBM=∠FBM.
在△BGM和△BFM中,
,
∴△BGM≌△BFM(AAS),
∴BG=BF=12,
∴AG=BG=AB=6,
∵点M在GH上,
∴点M到AD的距离等于AG=6,即点M在GH上运动,
∴点E与点C重合时,点M与点H重合.
当点E与点D重合时,如图,
∵△BGM≌△BFM,
∴MG=MF,
由题意得:△BCE≌△BFE,
∴CD=DF=6.
∵四边形ADHG为矩形,
∴DH=AG=6.
设MG=MF=x,则MD=x+6,MH=GH﹣GM=12﹣x.
∵∠H=90°,
∴MD2=MH2+DH2,
∴(x+6)2=(12﹣x)2+62.
∴x=4.
∴MH=GH﹣GM=8.
∴当点E从点C运动到点D时,点M运动的路径长为线段HM的长等于8.
21世纪教育网(www.21cnjy.com)
同课章节目录
