9.1平移 同步练(含答案) 2024-2025学年数学苏科版七年级下册
文档属性
| 名称 | 9.1平移 同步练(含答案) 2024-2025学年数学苏科版七年级下册 |  | |
| 格式 | docx | ||
| 文件大小 | 387.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-03-29 22:06:18 | ||
图片预览

文档简介
9.1 平 移
第1课时 平移的概念
1. 甲骨文是我国的一种古代文字,是汉字的早期形式.下列甲骨文中,能用其中一部分平移得到的是 ( )
2. 如图,把△ABC沿着射线BC的方向平移到△DEF的位置.下列说法错误的是 ( )
A. 点B与点C是对应点 B. AB与DE是对应线段
C. ∠ACB与∠F是对应角 D. 平移的距离是线段CF的长
3. 身高1.62m的小明乘升降电梯从1楼上升到3楼,则此时小明的身高为 m.
4. 如图,把右面涂色部分的方格块先向 (填“上”或“下”)平移 格,再向 (填“左”或“右”)平移 格即可与左面两块涂色部分的方格块合成一个长方形的整体.
5. 如图,在△ABE中,AB=4cm,AE=3cm,∠BAE=20°.将△ABE沿着MN的方向平移2cm到△FCD的位置,则BC= cm,CF= cm,∠CFD的度数为 .
6. (2024·苏州期中)如图,将长为6、宽为4的长方形ABCD先向右平移2,再向下平移1,得到长方形A'B'C'D',则涂色部分的面积为 .
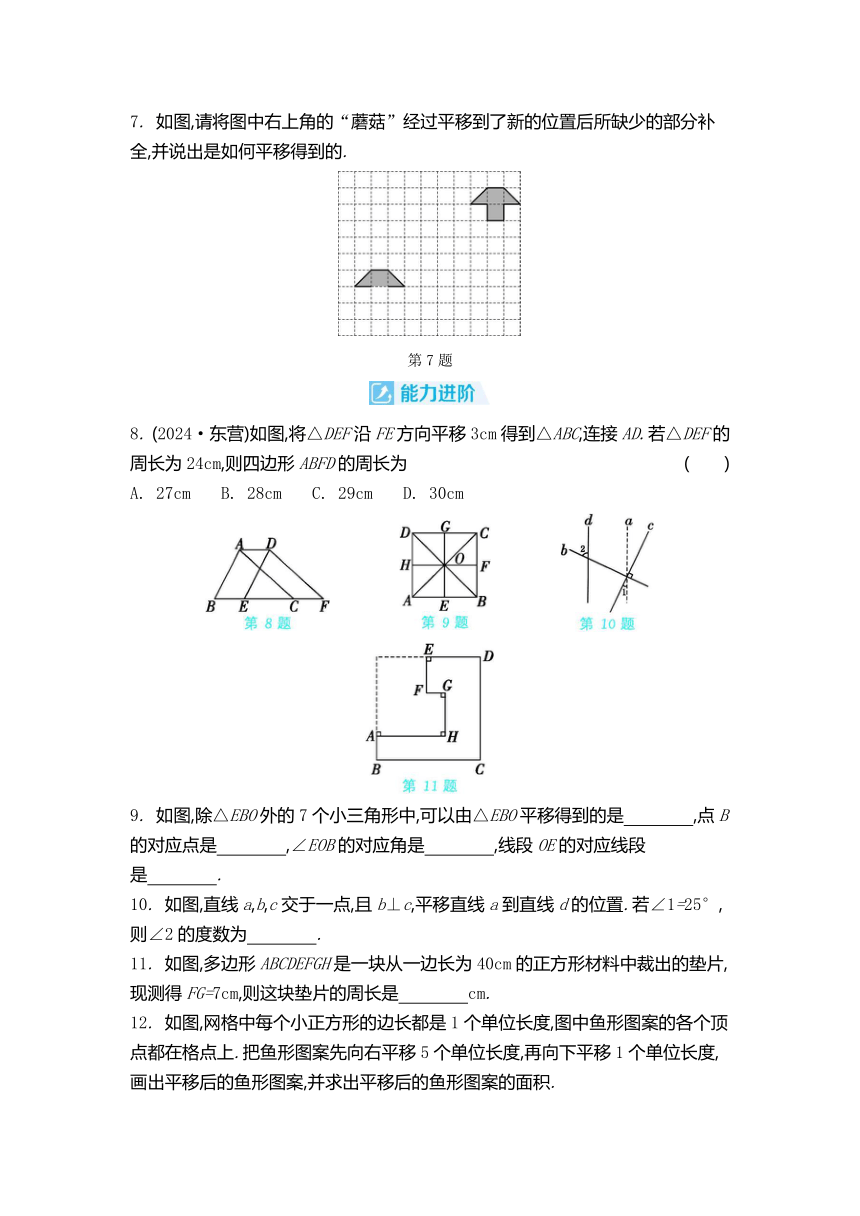
7. 如图,请将图中右上角的“蘑菇”经过平移到了新的位置后所缺少的部分补全,并说出是如何平移得到的.
第7题
8. (2024·东营)如图,将△DEF沿FE方向平移3cm得到△ABC,连接AD.若△DEF的周长为24cm,则四边形ABFD的周长为 ( )
A. 27cm B. 28cm C. 29cm D. 30cm
9. 如图,除△EBO外的7个小三角形中,可以由△EBO平移得到的是 ,点B的对应点是 ,∠EOB的对应角是 ,线段OE的对应线段是 .
10. 如图,直线a,b,c交于一点,且b⊥c,平移直线a到直线d的位置.若∠1=25°,则∠2的度数为 .
11. 如图,多边形ABCDEFGH是一块从一边长为40cm的正方形材料中裁出的垫片,现测得FG=7cm,则这块垫片的周长是 cm.
12. 如图,网格中每个小正方形的边长都是1个单位长度,图中鱼形图案的各个顶点都在格点上.把鱼形图案先向右平移5个单位长度,再向下平移1个单位长度,画出平移后的鱼形图案,并求出平移后的鱼形图案的面积.
第12题
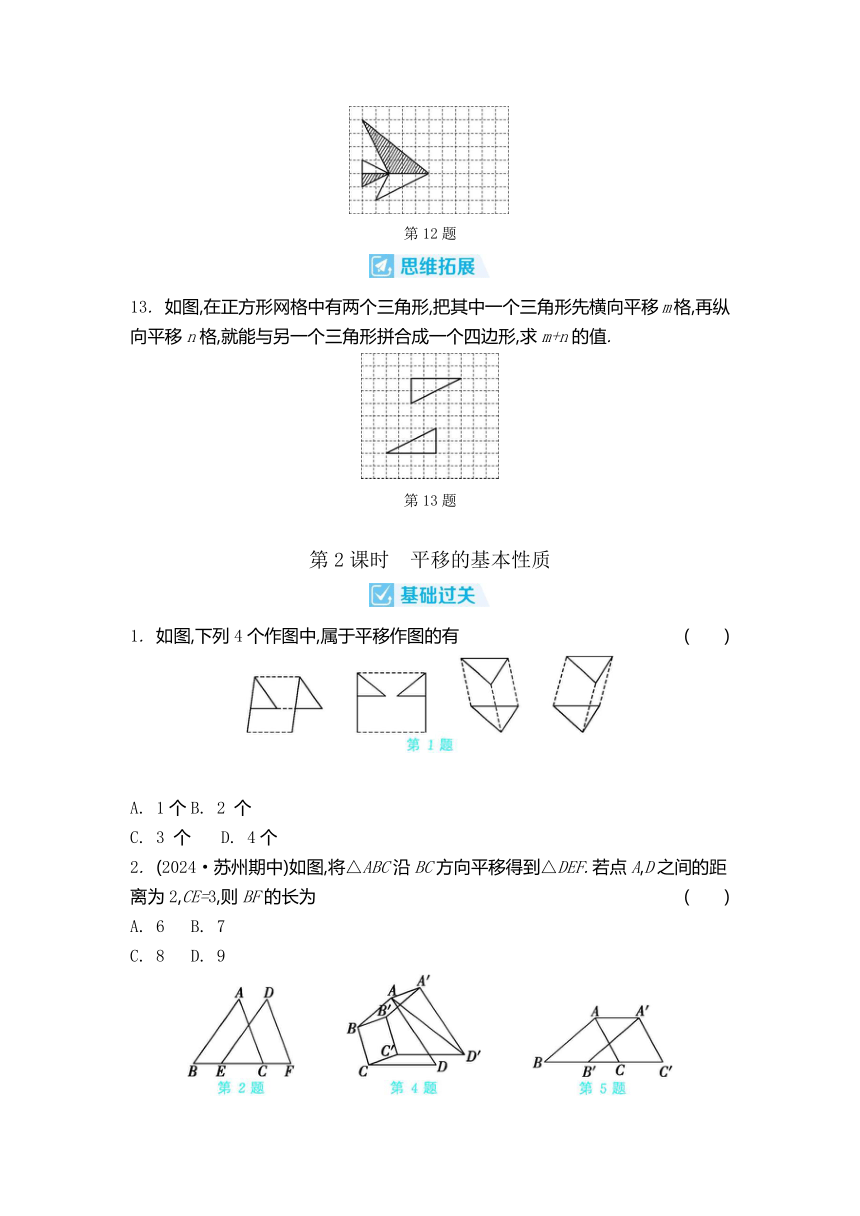
13. 如图,在正方形网格中有两个三角形,把其中一个三角形先横向平移m格,再纵向平移n格,就能与另一个三角形拼合成一个四边形,求m+n的值.
第13题
第2课时 平移的基本性质
1. 如图,下列4个作图中,属于平移作图的有 ( )
A. 1个 B. 2 个
C. 3 个 D. 4个
2. (2024·苏州期中)如图,将△ABC沿BC方向平移得到△DEF.若点A,D之间的距离为2,CE=3,则BF的长为 ( )
A. 6 B. 7
C. 8 D. 9
3. 将字母“N”沿着某一方向平移一定的距离,在作图中,第一步是在字母上找出关键的 个点.
4. 如图,四边形A'B'C'D'是由四边形ABCD平移得到的.
(1) 若BB'=3,AD=7,则AD'长的取值范围是 ;
(2) 分别连接CC',AA',则CC'与AA'的关系为 .
5. 如图,将△ABC沿BC方向平移,A',B'分别是点A,B的对应点,且BB'=3,连接AA'.若四边形ABC'A'的周长为16,则△ABC的周长是 .
6. 如图,△DEF是由△ABC平移得到的,△ABC的顶点A平移到了点D处,请画出平移前的△ABC.
第7题
7. 如图,在△ABC中,∠BAC=90°,把△ABC沿着直线BC向右平移5cm后得到△DEF,连接AE,AD.有以下结论:① AC∥DF;② ∠ADE=∠DEF;③ CF=5cm;④ DE⊥AC.其中,正确的有 ( )
A. 1个 B. 2个
C. 3个 D. 4个
8. “方胜”是我国古代妇女的一种发饰,其图案由两个能完全重合的正方形相叠组成,寓意是同心吉祥.如图,将正方形ABCD沿对角线BD方向平移1cm得到正方形A'B'C'D',形成一个“方胜”图案.若BD'=3.8cm,则点D,B'之间的距离为 ( )
A. 2cm B. 1.4cm C. 0.4cm D. 1.8cm
9. 如图,将△ABE沿着MN的方向平移到△FCD的位置.若∠BAE=20°,∠ABE=41°,则∠CDE+∠CFA的度数为 .
10. 如图,在△ABC中,AB=4cm,BC=5cm,AC=3cm,将△ABC沿BC方向平移acm(a<5)得到△DEF,且AC与DE相交于点G,连接AD,则涂色部分的周长为 cm.
11. 如图,在△ABC中,∠B=90°,AB=7,将△ABC沿BC方向平移至△DEF的位置,AC交DE于点G.若四边形DGCF的面积为30,且DG=2,则CF的长为 .
12. 如图,将面积为5的△ABC沿BC方向平移至△DEF的位置,平移的距离是边BC长的2倍.
(1) 线段AC与DF的关系是 ;
(2) 求四边形ACED的面积.
第12题
13. 如图①,将△ABD沿BD所在直线向右平移,得到△A'B'D',C为BD的延长线上一点,A'B'交AC于点E,AD平分∠BAC.
(1) 猜想∠B'EC与∠A'之间的数量关系,并说明理由.
(2) 如图②,将△ABD平移至△A'B'D'的位置,点A'在AC上,则A'D'平分∠B'A'C吗 为什么
9.1 平 移
第1课时 平移的概念
1. D 2. A 3. 1.62 4. 下 2 左 5 5. 2 4 20°
6. 12
7. 如图所示 答案不唯一,如先向下平移5格,再向左平移7格
8. D 9. △HOD 点O ∠HDO DH 10. 65° 11. 174
12. 画出平移后的鱼形图案如图所示 平移后的鱼形图案的面积为×2×2+×3×4+×3×2=11
13. 当两斜边重合时可组成一个长方形,此时m=2,n=4,则m+n=6.当两直角边重合时有两种情况:① 短直角边重合,此时m=2,n=4,则m+n=6;② 长直角边重合,此时m=2,n=6,则m+n=8.综上所述,m+n=6或8
第2课时 平移的基本性质
1. C 2. B 3. 4 4. (1) 46. 如图所示
7. D 8. D 9. 41°
10. 12 解析:因为△ABC沿BC方向平移acm(a<5)得到△DEF,所以AD=BE=acm,DE=AB=4cm.因为CE=BC-BE=(5-a)cm,所以涂色部分的周长为AD+CE+AC+DE=a+5-a+3+4=12(cm).
11. 5 解析:根据题意,可知△ABC的面积与△DEF的面积相等,AB∥DE,AB=DE=7,BC=EF.所以梯形ABEG的面积与四边形DGCF的面积相等,GE=DE-DG=5,所以×(7+5)·BE=30,解得BE=5.由平移的基本性质,得BE=CF,所以CF=5.
12. (1) 平行且相等 (2) 设点A到BC的距离为h,则△ABC的面积为BC·h=5.因为平移的距离是边BC长的2倍,所以AD=2BC,CE=BC.根据平移的基本性质,得AD∥CE,所以四边形ACED的面积为(AD+CE)·h=(2BC+BC)·h=3×BC·h=3×5=15
13. (1) ∠B'EC=2∠A' 理由:因为△A'B'D'是由△ABD沿BD所在直线向右平移得到的,所以∠BAD=∠A',AB∥A'B',所以∠BAC=∠B'EC.因为AD平分∠BAC,所以∠BAC=2∠BAD,所以∠B'EC=2∠A'. (2) A'D'平分∠B'A'C 因为△A'B'D'是由△ABD平移得到的,所以∠B'A'D'=∠BAD,AB∥A'B',所以∠BAC=∠B'A'C.因为AD平分∠BAC,所以∠BAD=∠BAC,所以∠B'A'D'=∠B'A'C,所以A'D'平分∠B'A'C
第1课时 平移的概念
1. 甲骨文是我国的一种古代文字,是汉字的早期形式.下列甲骨文中,能用其中一部分平移得到的是 ( )
2. 如图,把△ABC沿着射线BC的方向平移到△DEF的位置.下列说法错误的是 ( )
A. 点B与点C是对应点 B. AB与DE是对应线段
C. ∠ACB与∠F是对应角 D. 平移的距离是线段CF的长
3. 身高1.62m的小明乘升降电梯从1楼上升到3楼,则此时小明的身高为 m.
4. 如图,把右面涂色部分的方格块先向 (填“上”或“下”)平移 格,再向 (填“左”或“右”)平移 格即可与左面两块涂色部分的方格块合成一个长方形的整体.
5. 如图,在△ABE中,AB=4cm,AE=3cm,∠BAE=20°.将△ABE沿着MN的方向平移2cm到△FCD的位置,则BC= cm,CF= cm,∠CFD的度数为 .
6. (2024·苏州期中)如图,将长为6、宽为4的长方形ABCD先向右平移2,再向下平移1,得到长方形A'B'C'D',则涂色部分的面积为 .
7. 如图,请将图中右上角的“蘑菇”经过平移到了新的位置后所缺少的部分补全,并说出是如何平移得到的.
第7题
8. (2024·东营)如图,将△DEF沿FE方向平移3cm得到△ABC,连接AD.若△DEF的周长为24cm,则四边形ABFD的周长为 ( )
A. 27cm B. 28cm C. 29cm D. 30cm
9. 如图,除△EBO外的7个小三角形中,可以由△EBO平移得到的是 ,点B的对应点是 ,∠EOB的对应角是 ,线段OE的对应线段是 .
10. 如图,直线a,b,c交于一点,且b⊥c,平移直线a到直线d的位置.若∠1=25°,则∠2的度数为 .
11. 如图,多边形ABCDEFGH是一块从一边长为40cm的正方形材料中裁出的垫片,现测得FG=7cm,则这块垫片的周长是 cm.
12. 如图,网格中每个小正方形的边长都是1个单位长度,图中鱼形图案的各个顶点都在格点上.把鱼形图案先向右平移5个单位长度,再向下平移1个单位长度,画出平移后的鱼形图案,并求出平移后的鱼形图案的面积.
第12题
13. 如图,在正方形网格中有两个三角形,把其中一个三角形先横向平移m格,再纵向平移n格,就能与另一个三角形拼合成一个四边形,求m+n的值.
第13题
第2课时 平移的基本性质
1. 如图,下列4个作图中,属于平移作图的有 ( )
A. 1个 B. 2 个
C. 3 个 D. 4个
2. (2024·苏州期中)如图,将△ABC沿BC方向平移得到△DEF.若点A,D之间的距离为2,CE=3,则BF的长为 ( )
A. 6 B. 7
C. 8 D. 9
3. 将字母“N”沿着某一方向平移一定的距离,在作图中,第一步是在字母上找出关键的 个点.
4. 如图,四边形A'B'C'D'是由四边形ABCD平移得到的.
(1) 若BB'=3,AD=7,则AD'长的取值范围是 ;
(2) 分别连接CC',AA',则CC'与AA'的关系为 .
5. 如图,将△ABC沿BC方向平移,A',B'分别是点A,B的对应点,且BB'=3,连接AA'.若四边形ABC'A'的周长为16,则△ABC的周长是 .
6. 如图,△DEF是由△ABC平移得到的,△ABC的顶点A平移到了点D处,请画出平移前的△ABC.
第7题
7. 如图,在△ABC中,∠BAC=90°,把△ABC沿着直线BC向右平移5cm后得到△DEF,连接AE,AD.有以下结论:① AC∥DF;② ∠ADE=∠DEF;③ CF=5cm;④ DE⊥AC.其中,正确的有 ( )
A. 1个 B. 2个
C. 3个 D. 4个
8. “方胜”是我国古代妇女的一种发饰,其图案由两个能完全重合的正方形相叠组成,寓意是同心吉祥.如图,将正方形ABCD沿对角线BD方向平移1cm得到正方形A'B'C'D',形成一个“方胜”图案.若BD'=3.8cm,则点D,B'之间的距离为 ( )
A. 2cm B. 1.4cm C. 0.4cm D. 1.8cm
9. 如图,将△ABE沿着MN的方向平移到△FCD的位置.若∠BAE=20°,∠ABE=41°,则∠CDE+∠CFA的度数为 .
10. 如图,在△ABC中,AB=4cm,BC=5cm,AC=3cm,将△ABC沿BC方向平移acm(a<5)得到△DEF,且AC与DE相交于点G,连接AD,则涂色部分的周长为 cm.
11. 如图,在△ABC中,∠B=90°,AB=7,将△ABC沿BC方向平移至△DEF的位置,AC交DE于点G.若四边形DGCF的面积为30,且DG=2,则CF的长为 .
12. 如图,将面积为5的△ABC沿BC方向平移至△DEF的位置,平移的距离是边BC长的2倍.
(1) 线段AC与DF的关系是 ;
(2) 求四边形ACED的面积.
第12题
13. 如图①,将△ABD沿BD所在直线向右平移,得到△A'B'D',C为BD的延长线上一点,A'B'交AC于点E,AD平分∠BAC.
(1) 猜想∠B'EC与∠A'之间的数量关系,并说明理由.
(2) 如图②,将△ABD平移至△A'B'D'的位置,点A'在AC上,则A'D'平分∠B'A'C吗 为什么
9.1 平 移
第1课时 平移的概念
1. D 2. A 3. 1.62 4. 下 2 左 5 5. 2 4 20°
6. 12
7. 如图所示 答案不唯一,如先向下平移5格,再向左平移7格
8. D 9. △HOD 点O ∠HDO DH 10. 65° 11. 174
12. 画出平移后的鱼形图案如图所示 平移后的鱼形图案的面积为×2×2+×3×4+×3×2=11
13. 当两斜边重合时可组成一个长方形,此时m=2,n=4,则m+n=6.当两直角边重合时有两种情况:① 短直角边重合,此时m=2,n=4,则m+n=6;② 长直角边重合,此时m=2,n=6,则m+n=8.综上所述,m+n=6或8
第2课时 平移的基本性质
1. C 2. B 3. 4 4. (1) 4
7. D 8. D 9. 41°
10. 12 解析:因为△ABC沿BC方向平移acm(a<5)得到△DEF,所以AD=BE=acm,DE=AB=4cm.因为CE=BC-BE=(5-a)cm,所以涂色部分的周长为AD+CE+AC+DE=a+5-a+3+4=12(cm).
11. 5 解析:根据题意,可知△ABC的面积与△DEF的面积相等,AB∥DE,AB=DE=7,BC=EF.所以梯形ABEG的面积与四边形DGCF的面积相等,GE=DE-DG=5,所以×(7+5)·BE=30,解得BE=5.由平移的基本性质,得BE=CF,所以CF=5.
12. (1) 平行且相等 (2) 设点A到BC的距离为h,则△ABC的面积为BC·h=5.因为平移的距离是边BC长的2倍,所以AD=2BC,CE=BC.根据平移的基本性质,得AD∥CE,所以四边形ACED的面积为(AD+CE)·h=(2BC+BC)·h=3×BC·h=3×5=15
13. (1) ∠B'EC=2∠A' 理由:因为△A'B'D'是由△ABD沿BD所在直线向右平移得到的,所以∠BAD=∠A',AB∥A'B',所以∠BAC=∠B'EC.因为AD平分∠BAC,所以∠BAC=2∠BAD,所以∠B'EC=2∠A'. (2) A'D'平分∠B'A'C 因为△A'B'D'是由△ABD平移得到的,所以∠B'A'D'=∠BAD,AB∥A'B',所以∠BAC=∠B'A'C.因为AD平分∠BAC,所以∠BAD=∠BAC,所以∠B'A'D'=∠B'A'C,所以A'D'平分∠B'A'C
同课章节目录
- 第7章 平面图形的认识(二)
- 7.1 探索直线平行的条件
- 7.2 探索平行线的性质
- 7.3 图形的平移
- 7.4 认识三角形
- 7.5 多边形的内角和与外角和
- 第8章 幂的运算
- 8.1 同底数幂的乘法
- 8.2 幂的乘方与积的乘方
- 8.3 同底数幂的除法
- 第9章 整式乘法与因式分解
- 9.1 单项式乘单项式
- 9.2 单项式乘多项式
- 9.3 多项式乘多项式
- 9.4 乘法公式
- 9.5 多项式的因式分解
- 第10章 二元一次方程组
- 10.1 二元一次方程
- 10.2 二元一次方程组
- 10.3 解二元一次方程组
- 10.4 三元一次方程组
- 10.5 用二元一次方程解决问题
- 第11章 一元一次不等式
- 11.1 生活中的不等式
- 11.2 不等式的解集
- 11.3 不等式的性质
- 11.4 解一元一次不等式
- 11.5 用一元一次不等式解决问题
- 11.6 一元一次不等式组
- 第12章 证明
- 12.1 定义与命题
- 12.2 证明
- 12.3 互逆命题
