9.2轴对称 同步练(含答案) 2024-2025学年数学苏科版七年级下册
文档属性
| 名称 | 9.2轴对称 同步练(含答案) 2024-2025学年数学苏科版七年级下册 |
|
|
| 格式 | docx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-03-29 00:00:00 | ||
图片预览


文档简介
9.2 轴 对 称
第1课时 轴对称的概念
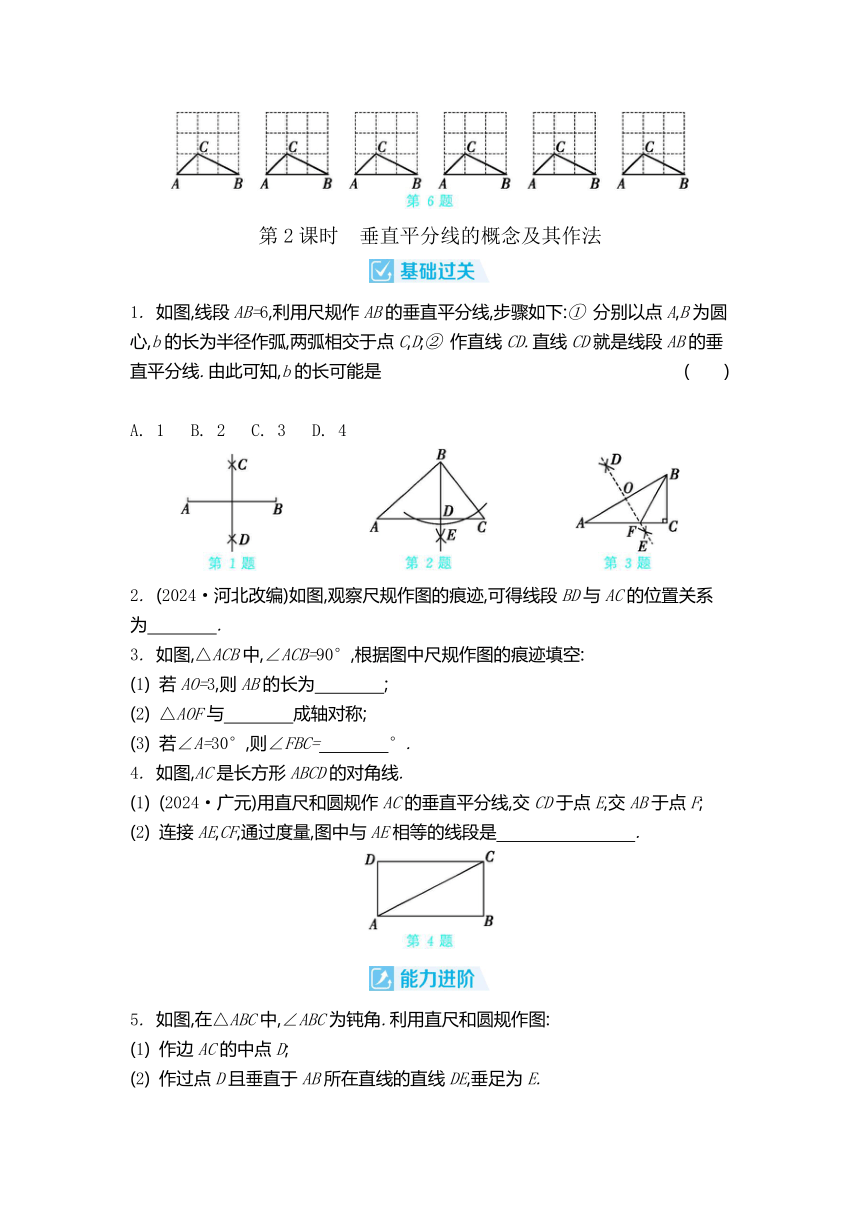
1. (2024·盐城)下列生活现象里的主体事物,在现实运动中属于翻折的是 ( )
A. 工作中的雨刮器 B. 移动中的黑板
C. 折叠中的纸片 D. 骑行中的自行车
2. 在下列四组图中,左右两图成轴对称的是 ( )
3. 若在镜子中看到的一串数字是“”,则这串数字是“ ”.
4. 如图,将△ABC折叠,使点A与边BC上的中点D重合,折痕为MN.若AB=9,BC=6,则△DNB的周长为 .
5. 如图,网格图中每个小正方形的边长均为1,点A,B,C都在格点上.
(1) 画出△ABC关于直线MN对称的△A1B1C1;
(2) 求△A1B1C1的面积;
(3) 连接AA1,CC1,求四边形CAA1C1的面积.
第5题
6. 如图,在3×3的正方形格点图中,△ABC是格点三角形,若有另一个格点△DFE与△ABC关于某条直线成轴对称,请在下面的图中尽可能多地画出△DFE.
第2课时 垂直平分线的概念及其作法
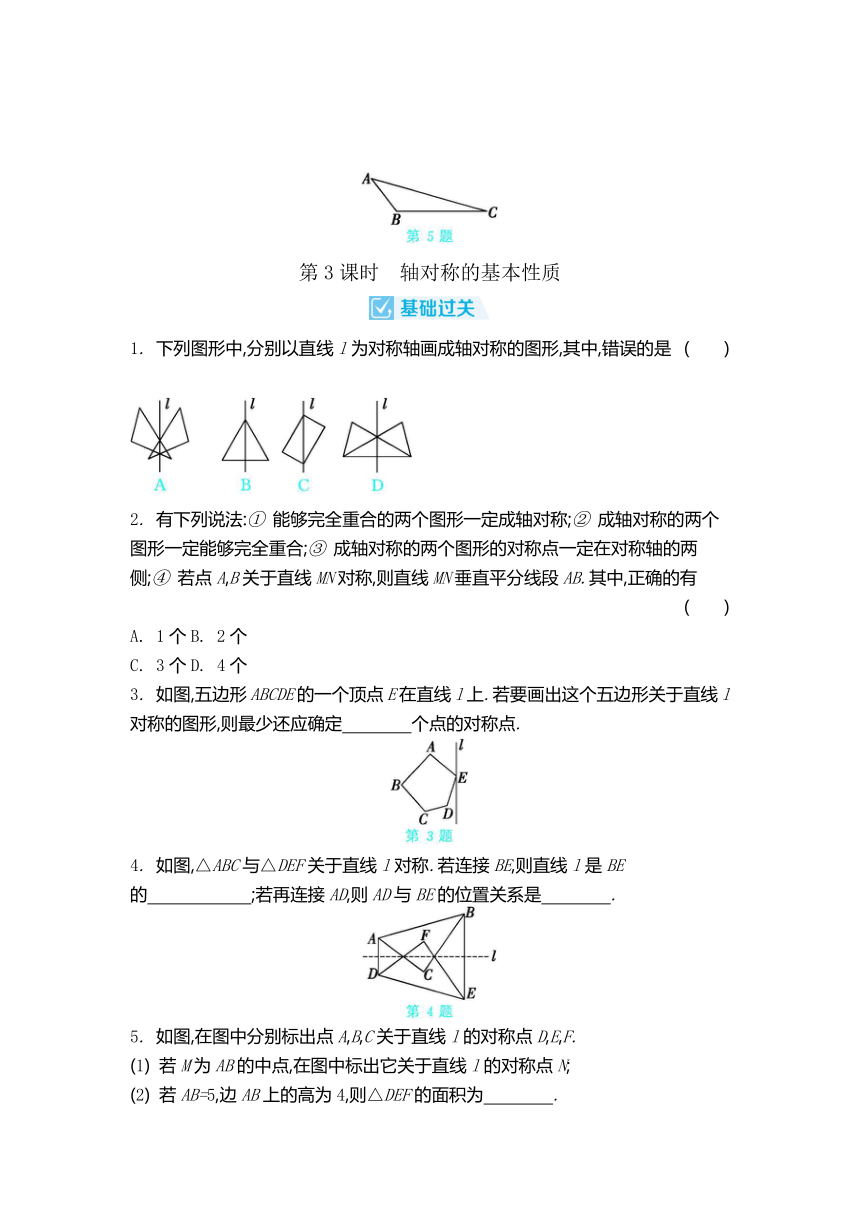
1. 如图,线段AB=6,利用尺规作AB的垂直平分线,步骤如下:① 分别以点A,B为圆心,b的长为半径作弧,两弧相交于点C,D;② 作直线CD.直线CD就是线段AB的垂直平分线.由此可知,b的长可能是 ( )
A. 1 B. 2 C. 3 D. 4
2. (2024·河北改编)如图,观察尺规作图的痕迹,可得线段BD与AC的位置关系为 .
3. 如图,△ACB中,∠ACB=90°,根据图中尺规作图的痕迹填空:
(1) 若AO=3,则AB的长为 ;
(2) △AOF与 成轴对称;
(3) 若∠A=30°,则∠FBC= °.
4. 如图,AC是长方形ABCD的对角线.
(1) (2024·广元)用直尺和圆规作AC的垂直平分线,交CD于点E,交AB于点F;
(2) 连接AE,CF,通过度量,图中与AE相等的线段是 .
5. 如图,在△ABC中,∠ABC为钝角.利用直尺和圆规作图:
(1) 作边AC的中点D;
(2) 作过点D且垂直于AB所在直线的直线DE,垂足为E.
第3课时 轴对称的基本性质
1. 下列图形中,分别以直线l为对称轴画成轴对称的图形,其中,错误的是 ( )
2. 有下列说法:① 能够完全重合的两个图形一定成轴对称;② 成轴对称的两个图形一定能够完全重合;③ 成轴对称的两个图形的对称点一定在对称轴的两侧;④ 若点A,B关于直线MN对称,则直线MN垂直平分线段AB.其中,正确的有 ( )
A. 1个 B. 2个
C. 3个 D. 4个
3. 如图,五边形ABCDE的一个顶点E在直线l上.若要画出这个五边形关于直线l对称的图形,则最少还应确定 个点的对称点.
4. 如图,△ABC与△DEF关于直线l对称.若连接BE,则直线l是BE的 ;若再连接AD,则AD与BE的位置关系是 .
5. 如图,在图中分别标出点A,B,C关于直线l的对称点D,E,F.
(1) 若M为AB的中点,在图中标出它关于直线l的对称点N;
(2) 若AB=5,边AB上的高为4,则△DEF的面积为 .
6. 如图,以直线l为对称轴,画出图形的另一半.
7. (2024·河北)如图,AD与BC交于点O,△ABO和△CDO关于直线PQ对称,点A,B的对称点分别是C,D.下列结论不一定正确的是 ( )
A. AD⊥BC B. 若连接AC,则AC⊥PQ
C. △ABO与△CDO能完全重合 D. 若连接AC,BD,则AC∥BD
8. 如图,有一个英语单词,四个字母都关于直线l对称.若补全字母,则这个单词所指的物品是 .
9. 如图,直线l1⊥l2,分别画出线段MN关于直线l1和l2的对称线段M1N1和M2N2,则线段M1N1和M2N2 (填“成”或“不成”)轴对称.
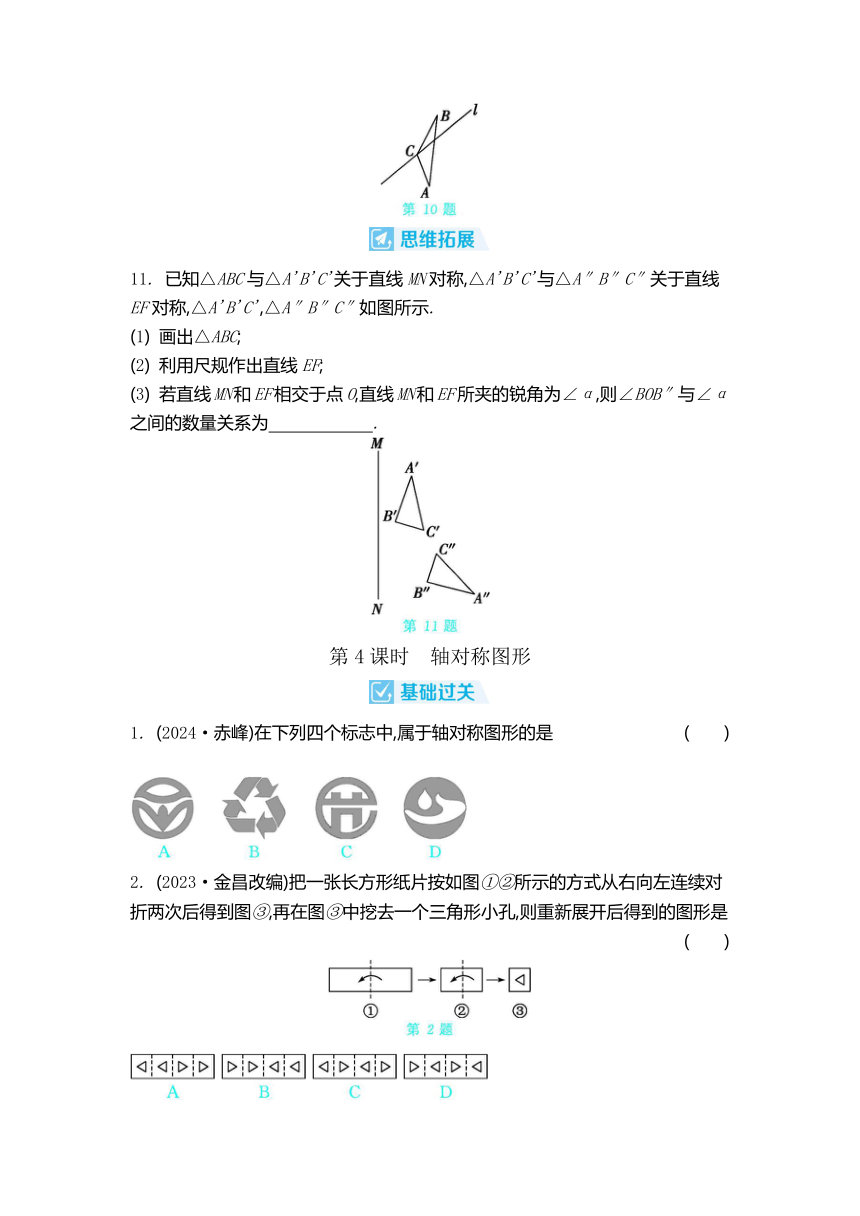
10. 如图,△ABC的顶点C在直线l上,用直尺和圆规作△ABC关于直线l对称的△EDC.
11. 已知△ABC与△A'B'C'关于直线MN对称,△A'B'C'与△A″B″C″关于直线EF对称,△A'B'C',△A″B″C″如图所示.
(1) 画出△ABC;
(2) 利用尺规作出直线EF;
(3) 若直线MN和EF相交于点O,直线MN和EF所夹的锐角为∠α,则∠BOB″与∠α之间的数量关系为 .
第4课时 轴对称图形
1. (2024·赤峰)在下列四个标志中,属于轴对称图形的是 ( )
2. (2023·金昌改编)把一张长方形纸片按如图①②所示的方式从右向左连续对折两次后得到图③,再在图③中挖去一个三角形小孔,则重新展开后得到的图形是 ( )
3. (2023·长沙改编)在如图所示的图形中,对称轴条数最多的是 (填序号),共有 条对称轴;只有1条对称轴的是 (填序号).
① ② ③ ④
4. 如图①②③所示为由小正方形组成的“7”字形图案,请你用不同的方法分别在图中添画一个小正方形,使它们成为轴对称图形.
5. 某居民小区进行绿化建设,要在一块长方形空地上建花坛(如图).现征集设计方案,要求设计的图案由圆和正方形组成(圆和正方形的个数不限),并且使整块长方形空地成为轴对称图形.请你画出一种符合要求的图案.
6. (2024·天津)如图,在△ABC中,∠C=90°,∠B=40°,根据尺规作图的痕迹作射线AP,与BC相交于点D,则∠ADC的度数为 ( )
第6题
A. 60°
B. 65°
C. 70°
D. 75°
7. (2024·甘肃)围棋起源于中国,古代称为“弈”.如图所示为两位同学的部分对弈图,轮到白方落子,观察棋盘,白方如果落子于点 的位置,那么所得的对弈图是轴对称图形(点A,B,C,D位于棋盘的格点上).
8. 如图,在4×4的正方形网格中,已有三个小正方形被涂灰,再将网格中其余小正方形任意涂灰一个,使整个涂灰部分组成的图案构成一个轴对称图形的方法有 种.
9. 如图,三角形④与哪些三角形成轴对称 整个图形是轴对称图形吗 如果是,那么它共有几条对称轴 请把它们画出来.
第9题
10. 如图,现有两张完全一样的直角三角形纸片,将它们的一组对应边重合在一起能组成轴对称图形,请画出所有组成的轴对称图形及其对称轴(三角形不重叠).
第10题
9.3 旋 转
第1课时 旋转的概念
1. 下列运动中,属于旋转的是 ( )
A. 小明向北走了4米 B. 树叶从空中落下
C. 电梯从1楼到12楼 D. 小明在荡秋千
2. 如图,将正方形ABCD中的涂色三角形绕点A按顺时针方向旋转90°后,得到的图形为 ( )
3. 如图,△ABC和△DEC都是直角三角形,其中一个三角形是由另一个三角形旋转得到的.下列说法中,错误的是 ( )
A. 旋转中心是点C B. 旋转的角度是90°或270°
C. 既可以逆时针旋转,也可以顺时针旋转 D. 旋转中心是点B,旋转的角度是180°
4. 如图所示的图案由三个叶片组成,绕点O旋转120°后可以和自身重合.若每个叶片的面积为4cm2,∠AOB为120°,则图中阴影部分的面积为 cm2.
5. 如图,将△AOC 逆时针旋转到△BOD,其中∠AOC=120°,点A,O,D在同一条直线上.
(1) 点A的对应点是 ;
(2) ∠AOC的对应角是 ;
(3) 线段AC的对应线段是 ;
(4) 旋转的角度为 °.
6. (2024·济宁改编)如图,△ABC的三个顶点均在格点上.
(1) 将△ABC向下平移2个单位长度得到△A1B1C1,画出平移后的图形;
(2) 将△A1B1C1绕点B1逆时针旋转90°得到△A2B1C2,画出旋转后的图形.
7. 如图,在△ABC中,AB=AC.若M是BC边上任意一点,将△ABM绕点A按逆时针方向旋转得到△ACN,点M的对应点为N,连接MN,则下列结论一定正确的是 ( )
A. AB=AN B. AB∥NC C. ∠AMN=∠ACN D. MN⊥AC
8. 如图,在△ABC中,∠ABC=∠ACB=75°.将△ABC绕点C旋转,得到△DEC,点A的对应点D在BC的延长线上,则旋转的方向和旋转的角度可能为 ( )
A. 逆时针,30° B. 逆时针,105° C. 顺时针,30° D. 顺时针,105°
9. (2024·雅安)如图,在△ABC和△ADE中,∠ABC=70°,∠BAC=∠DAE=40°,将△ADE绕点A顺时针旋转一定角度,当AD∥BC时,∠BAE的度数是 .
10. (2024·安徽)如图,在由边长为1个单位长度的小正方形组成的网格中,点A,B,C,D均在格点上.
(1) 以点D为旋转中心,将△ABC旋转180°得到△A1B1C1,画出△A1B1C1;
(2) 求出以B,C1,B1,C为顶点的四边形的面积;
(3) 在BC上确定一个格点E,使得BC=2BE.
第10题
11. (2023·宁夏改编)如图,在△ABC中,∠ABC=∠C=45°,BC=2,点D在边BC上,且BD∶CD=1∶3,连接AD,将△ADC绕点A顺时针旋转90°得到△AEB,连接DE,求△BDE的面积.
第11题
第2课时 旋转的基本性质
1. 下列说法中,正确的是 ( )
A. 旋转改变图形的形状和大小
B. 在旋转过程中,图形的每个点移动的距离相等
C. 经过旋转,图形的对应线段、对应角分别相等
D. 经过旋转,图形的对应点的连线平行且相等
2. 如图,在△ABC中,∠BAC=90°,将其绕点C逆时针旋转48°得到△A'B'C,点A在边B'C上,则∠B'的度数为 ( )
A. 42° B. 48°
C. 52° D. 58°
3. 如图,△ABC为直角三角形,∠ACB=90°,BC=3cm,AC=4cm,将△ABC绕点C逆时针旋转90°后得到△EDC,则∠B=∠ ,CE= cm,AD= cm,DE与AB的位置关系是 .
4. (2023·张家界)如图,AO为∠BAC的平分线,且∠BAC=50°,将四边形ABOC绕点A按逆时针方向旋转后,得到四边形AB'O'C',且∠OAC'=100°,则四边形ABOC旋转的角度为 .
5. 在如图所示的由相同小正方形组成的网格图中,点O和△ABC的三个顶点均在格点(网格线的交点)上,画出△ABC绕点O顺时针旋转90°后得到的△A1B1C1.
6. (2024·陕西改编)如图,在△AOB中,∠AOB=90°,将△AOB绕点O顺时针旋转45°,得到△A'OB',图中互相垂直的两条线段所在的直线有 ( )
A. 1组 B. 2组 C. 3组 D. 4组
7. 如图,在4×4的方格纸中,△MNP绕某点旋转一定的角度,得到△M1N1P1,则其旋转中心一定是点 .
8. 如图,教室里有一只倒地的簸箕,BC与地面的夹角为50°,∠DCB=25°,小明同学将它扶起平放在地面上(点C不动),则簸箕柄AB绕点C转动的角度为 .
9. 将一副三角尺按如图所示的方式叠放在一起,其中点B,D重合.若固定三角尺AOB,将三角尺ACD绕点A顺时针旋转一周,则当旋转的角度为 时,CD∥AO.
10. 如图,四边形ABCD绕点O旋转后,顶点A的对应点为E,试确定点B,C,D的对应点的位置,并画出旋转后的四边形.
11. 如图,在由边长均为1个单位长度的小正方形组成的网格中,△A'B'C'是由△ABC通过图形变换或变换组合(平移、轴对称、旋转)得到的,请你写出一种方案.
第11题
第3课时 中心对称与中心对称图形
1. (2024·德州)下列图形是中心对称图形的为 ( )
2. 若点M,N关于点O中心对称,则下列说法不正确的是 ( )
A. OM=ON B. 点M,O,N在同一条直线上
C. △OMN是等腰三角形 D. 线段OM绕点O旋转180°能与线段ON重合
3. 如图,△AOB与△DOC成中心对称,△AOB的面积是6,AB=3,则△DOC的边CD上的高是 .
4. (2024·牡丹江改编)如图所示为四个图形,其中图④是等腰三角形.
(1) 属于轴对称图形的有 (填序号),它们的对称轴分别有 条;
(2) 图①②分别至少旋转 °, °时,能与原图形互相重合;
(3) 属于中心对称图形的有 (填序号).
5. (1) 如图①所示为由边长为1的小等边三角形构成的网格,现有5个小等边三角形已涂上阴影,请在余下的空白小等边三角形中选取1个涂上阴影,使得6个阴影小等边三角形组成一个中心对称图形.
(2) 在如图②所示的网格中,选取2个空白小正方形涂上阴影,使6个阴影小正方形组成一个中心对称图形;在如图③所示的网格中,选取2个空白小正方形涂上阴影,使6个阴影小正方形组成一个轴对称图形,但不是中心对称图形.
6. 如图,△ABC与△A'B'C'关于点O成中心对称,则下列结论不一定成立的是 ( )
A. A'是点A关于点O的对称点 B. BO=B'O
C. AB∥A'B' D. ∠ABC=∠C'A'B'
7. 如图,直线a,b互相垂直且相交于点O,曲线C关于点O成中心对称,点A的对称点是A',AB⊥a于点B,A'D⊥b于点D.若OB=3,OD=2,则涂色部分的面积之和为 .
8. 如图所示为两张完全重合在一起的等边三角形硬纸片,点O是它们的中心.若按住下面的硬纸片不动,将上面的硬纸片绕点O按顺时针方向旋转,则旋转的角度至少为 时,两张硬纸片所构成的图形是中心对称图形.
9. 在正方形网格中,△ABC的顶点在格点上.请仅用无刻度的直尺完成以下作图.
(1) 如图①,作△ABC关于点O对称的△A'B'C';
(2) 如图②,作△ABC绕点A按顺时针方向旋转一定角度后,顶点仍在格点上的△AB'C'.
10. 如图,在△ABC中,D是边BC上的中点,连接AD.
(1) 画出与△ACD关于点D成中心对称的三角形;
(2) 在(1)的基础上找出与AC相等的线段;
(3) 在△ABC中,探索AB+AC与AD之间的数量关系,并说明理由.
第10题
9.2 轴 对 称
第1课时 轴对称的概念
1. C 2. C 3. 309087 4. 12
5. (1) 如图所示 (2) △A1B1C1的面积为3×5-×3×3-×2×2-×5×1=6 (3) 如图,四边形CAA1C1的面积为×(4+10)×3=21
6. 如图所示
第2课时 垂直平分线的概念及其作法
1. D 2. BD⊥AC 3. (1) 6 (2) △BOF (3) 30
4. (1) 如图,直线EF即为所求 (2) EC,CF,AF
5. (1) 如图,点D即为所求 (2) 如图,直线DE即为所求
第3课时 轴对称的基本性质
1. C 2. B 3. 4 4. 垂直平分线 平行
5. 如图所示 (1) 如图所示
(2) 10 解析:S△DEF=S△ABC=×5×4=10.
6. 如图所示
7. A 8. 书
9. 如图,线段M1N1和M2N2即为所求 不成
10. 如图,△EDC即为所求
11. (1) 如图,△ABC即为所求 (2) 如图,直线EF即为所求
(3) ∠BOB″=2∠α 解析:如图,连接BO,B'O,B″O.因为△ABC与△A'B'C'关于直线MN对称,所以∠BOM=∠B'OM.又因为△A'B'C'与△A″B″C″关于直线EF对称,所以∠B'OE=∠B″OE,所以∠BOB″=∠BOM+∠B'OM+∠B'OE+∠B″OE=2(∠B'OM+∠B'OE)=2∠MOE=2∠α.
第4课时 轴对称图形
1. A 2. C
3. ③ 8 ②⑥⑦⑧ 解析:如图,对称轴条数最多的是③,共有8条对称轴;只有1条对称轴的是②⑥⑦⑧.
① ② ③ ④
4. 如图①②③所示
5. 答案不唯一,如图所示
6. B 7. A或C
8. 4 解析:如图,涂灰①~④中任意一个均满足题意.
9. 三角形④分别与三角形②、三角形③成轴对称 整个图形是轴对称图形,它共有2条对称轴 如图,直线l1,l2就是整个图形的对称轴
10. 如图所示
9.3 旋 转
第1课时 旋转的概念
1. D 2. A 3. D 4. 4 5. (1) B (2) ∠BOD (3) BD (4) 60
6. (1) 如图,△A1B1C1即为所求 (2) 如图,△A2B1C2即为所求
7. C 8. D
9. 30°或150° 解析:当点D在点A的左侧时,∠BAE=30°;当点D在点A的右侧时,∠BAE=150°.
10. (1) 如图,△A1B1C1即为所求 (2) 以B,C1,B1,C为顶点的四边形的面积为10×8-2××2×4-2××4×8=40 (3) 如图,点E即为所求
11. 因为BC=2,BD∶CD=1∶3,所以BD=×BC=,DC=×BC=.因为将△ADC绕点A顺时针旋转90°得到△AEB,所以DC=EB=,∠ABE=∠C=45°.因为∠ABC=45°,所以∠EBD=90°,所以△BDE的面积为BD·EB=××=
第2课时 旋转的基本性质
1. C 2. A 3. EDC 4 1 垂直 4. 75°
5. 如图所示
6. D 7. B 8. 105°
9. 75°或255° 解析:如图①,当CD在OA的左侧,CD∥AO时,易得旋转的角度为45°+30°=75°;如图②,当CD在OA的右侧,CD∥OA时,易得旋转的角度为45°+180°+30°=255°.综上所述,当旋转的角度为75°或255°时,CD∥AO.
10. 如图,点B的对应点为F,点C的对应点为G,点D的对应点为H,四边形EFGH即为旋转后的四边形
11. 答案不唯一,如先将△ABC绕点A逆时针旋转90°,再向下平移2个单位长度,最后向右平移2个单位长度
第3课时 中心对称与中心对称图形
1. B 2. C 3. 4 4. (1) ①②③④ 4,3,2,1
(2) 90 120 (3) ①③
5. 答案不唯一,如(1) 如图①所示 (2) 如图②③所示
6. D 7. 6
8. 60° 解析:如图,至少旋转60°,两张硬纸片所构成的图形是中心对称图形.
9. (1) 如图①,△A'B'C'即为所求 (2) 如图②,△AB'C'即为所求
10. (1) 如图,延长AD至点A',使A'D=AD,连接A'B,则△A'BD就是与△ACD关于点D成中心对称的三角形 (2) A'B=AC (3) AB+AC>2AD 理由:因为△ACD与△A'BD关于点D成中心对称,所以AD=A'D,AC=A'B.在△ABA'中,根据两点之间,线段最短,得AB+A'B>AA',所以AB+AC>AD+A'D,即AB+AC>2AD.
第1课时 轴对称的概念
1. (2024·盐城)下列生活现象里的主体事物,在现实运动中属于翻折的是 ( )
A. 工作中的雨刮器 B. 移动中的黑板
C. 折叠中的纸片 D. 骑行中的自行车
2. 在下列四组图中,左右两图成轴对称的是 ( )
3. 若在镜子中看到的一串数字是“”,则这串数字是“ ”.
4. 如图,将△ABC折叠,使点A与边BC上的中点D重合,折痕为MN.若AB=9,BC=6,则△DNB的周长为 .
5. 如图,网格图中每个小正方形的边长均为1,点A,B,C都在格点上.
(1) 画出△ABC关于直线MN对称的△A1B1C1;
(2) 求△A1B1C1的面积;
(3) 连接AA1,CC1,求四边形CAA1C1的面积.
第5题
6. 如图,在3×3的正方形格点图中,△ABC是格点三角形,若有另一个格点△DFE与△ABC关于某条直线成轴对称,请在下面的图中尽可能多地画出△DFE.
第2课时 垂直平分线的概念及其作法
1. 如图,线段AB=6,利用尺规作AB的垂直平分线,步骤如下:① 分别以点A,B为圆心,b的长为半径作弧,两弧相交于点C,D;② 作直线CD.直线CD就是线段AB的垂直平分线.由此可知,b的长可能是 ( )
A. 1 B. 2 C. 3 D. 4
2. (2024·河北改编)如图,观察尺规作图的痕迹,可得线段BD与AC的位置关系为 .
3. 如图,△ACB中,∠ACB=90°,根据图中尺规作图的痕迹填空:
(1) 若AO=3,则AB的长为 ;
(2) △AOF与 成轴对称;
(3) 若∠A=30°,则∠FBC= °.
4. 如图,AC是长方形ABCD的对角线.
(1) (2024·广元)用直尺和圆规作AC的垂直平分线,交CD于点E,交AB于点F;
(2) 连接AE,CF,通过度量,图中与AE相等的线段是 .
5. 如图,在△ABC中,∠ABC为钝角.利用直尺和圆规作图:
(1) 作边AC的中点D;
(2) 作过点D且垂直于AB所在直线的直线DE,垂足为E.
第3课时 轴对称的基本性质
1. 下列图形中,分别以直线l为对称轴画成轴对称的图形,其中,错误的是 ( )
2. 有下列说法:① 能够完全重合的两个图形一定成轴对称;② 成轴对称的两个图形一定能够完全重合;③ 成轴对称的两个图形的对称点一定在对称轴的两侧;④ 若点A,B关于直线MN对称,则直线MN垂直平分线段AB.其中,正确的有 ( )
A. 1个 B. 2个
C. 3个 D. 4个
3. 如图,五边形ABCDE的一个顶点E在直线l上.若要画出这个五边形关于直线l对称的图形,则最少还应确定 个点的对称点.
4. 如图,△ABC与△DEF关于直线l对称.若连接BE,则直线l是BE的 ;若再连接AD,则AD与BE的位置关系是 .
5. 如图,在图中分别标出点A,B,C关于直线l的对称点D,E,F.
(1) 若M为AB的中点,在图中标出它关于直线l的对称点N;
(2) 若AB=5,边AB上的高为4,则△DEF的面积为 .
6. 如图,以直线l为对称轴,画出图形的另一半.
7. (2024·河北)如图,AD与BC交于点O,△ABO和△CDO关于直线PQ对称,点A,B的对称点分别是C,D.下列结论不一定正确的是 ( )
A. AD⊥BC B. 若连接AC,则AC⊥PQ
C. △ABO与△CDO能完全重合 D. 若连接AC,BD,则AC∥BD
8. 如图,有一个英语单词,四个字母都关于直线l对称.若补全字母,则这个单词所指的物品是 .
9. 如图,直线l1⊥l2,分别画出线段MN关于直线l1和l2的对称线段M1N1和M2N2,则线段M1N1和M2N2 (填“成”或“不成”)轴对称.
10. 如图,△ABC的顶点C在直线l上,用直尺和圆规作△ABC关于直线l对称的△EDC.
11. 已知△ABC与△A'B'C'关于直线MN对称,△A'B'C'与△A″B″C″关于直线EF对称,△A'B'C',△A″B″C″如图所示.
(1) 画出△ABC;
(2) 利用尺规作出直线EF;
(3) 若直线MN和EF相交于点O,直线MN和EF所夹的锐角为∠α,则∠BOB″与∠α之间的数量关系为 .
第4课时 轴对称图形
1. (2024·赤峰)在下列四个标志中,属于轴对称图形的是 ( )
2. (2023·金昌改编)把一张长方形纸片按如图①②所示的方式从右向左连续对折两次后得到图③,再在图③中挖去一个三角形小孔,则重新展开后得到的图形是 ( )
3. (2023·长沙改编)在如图所示的图形中,对称轴条数最多的是 (填序号),共有 条对称轴;只有1条对称轴的是 (填序号).
① ② ③ ④
4. 如图①②③所示为由小正方形组成的“7”字形图案,请你用不同的方法分别在图中添画一个小正方形,使它们成为轴对称图形.
5. 某居民小区进行绿化建设,要在一块长方形空地上建花坛(如图).现征集设计方案,要求设计的图案由圆和正方形组成(圆和正方形的个数不限),并且使整块长方形空地成为轴对称图形.请你画出一种符合要求的图案.
6. (2024·天津)如图,在△ABC中,∠C=90°,∠B=40°,根据尺规作图的痕迹作射线AP,与BC相交于点D,则∠ADC的度数为 ( )
第6题
A. 60°
B. 65°
C. 70°
D. 75°
7. (2024·甘肃)围棋起源于中国,古代称为“弈”.如图所示为两位同学的部分对弈图,轮到白方落子,观察棋盘,白方如果落子于点 的位置,那么所得的对弈图是轴对称图形(点A,B,C,D位于棋盘的格点上).
8. 如图,在4×4的正方形网格中,已有三个小正方形被涂灰,再将网格中其余小正方形任意涂灰一个,使整个涂灰部分组成的图案构成一个轴对称图形的方法有 种.
9. 如图,三角形④与哪些三角形成轴对称 整个图形是轴对称图形吗 如果是,那么它共有几条对称轴 请把它们画出来.
第9题
10. 如图,现有两张完全一样的直角三角形纸片,将它们的一组对应边重合在一起能组成轴对称图形,请画出所有组成的轴对称图形及其对称轴(三角形不重叠).
第10题
9.3 旋 转
第1课时 旋转的概念
1. 下列运动中,属于旋转的是 ( )
A. 小明向北走了4米 B. 树叶从空中落下
C. 电梯从1楼到12楼 D. 小明在荡秋千
2. 如图,将正方形ABCD中的涂色三角形绕点A按顺时针方向旋转90°后,得到的图形为 ( )
3. 如图,△ABC和△DEC都是直角三角形,其中一个三角形是由另一个三角形旋转得到的.下列说法中,错误的是 ( )
A. 旋转中心是点C B. 旋转的角度是90°或270°
C. 既可以逆时针旋转,也可以顺时针旋转 D. 旋转中心是点B,旋转的角度是180°
4. 如图所示的图案由三个叶片组成,绕点O旋转120°后可以和自身重合.若每个叶片的面积为4cm2,∠AOB为120°,则图中阴影部分的面积为 cm2.
5. 如图,将△AOC 逆时针旋转到△BOD,其中∠AOC=120°,点A,O,D在同一条直线上.
(1) 点A的对应点是 ;
(2) ∠AOC的对应角是 ;
(3) 线段AC的对应线段是 ;
(4) 旋转的角度为 °.
6. (2024·济宁改编)如图,△ABC的三个顶点均在格点上.
(1) 将△ABC向下平移2个单位长度得到△A1B1C1,画出平移后的图形;
(2) 将△A1B1C1绕点B1逆时针旋转90°得到△A2B1C2,画出旋转后的图形.
7. 如图,在△ABC中,AB=AC.若M是BC边上任意一点,将△ABM绕点A按逆时针方向旋转得到△ACN,点M的对应点为N,连接MN,则下列结论一定正确的是 ( )
A. AB=AN B. AB∥NC C. ∠AMN=∠ACN D. MN⊥AC
8. 如图,在△ABC中,∠ABC=∠ACB=75°.将△ABC绕点C旋转,得到△DEC,点A的对应点D在BC的延长线上,则旋转的方向和旋转的角度可能为 ( )
A. 逆时针,30° B. 逆时针,105° C. 顺时针,30° D. 顺时针,105°
9. (2024·雅安)如图,在△ABC和△ADE中,∠ABC=70°,∠BAC=∠DAE=40°,将△ADE绕点A顺时针旋转一定角度,当AD∥BC时,∠BAE的度数是 .
10. (2024·安徽)如图,在由边长为1个单位长度的小正方形组成的网格中,点A,B,C,D均在格点上.
(1) 以点D为旋转中心,将△ABC旋转180°得到△A1B1C1,画出△A1B1C1;
(2) 求出以B,C1,B1,C为顶点的四边形的面积;
(3) 在BC上确定一个格点E,使得BC=2BE.
第10题
11. (2023·宁夏改编)如图,在△ABC中,∠ABC=∠C=45°,BC=2,点D在边BC上,且BD∶CD=1∶3,连接AD,将△ADC绕点A顺时针旋转90°得到△AEB,连接DE,求△BDE的面积.
第11题
第2课时 旋转的基本性质
1. 下列说法中,正确的是 ( )
A. 旋转改变图形的形状和大小
B. 在旋转过程中,图形的每个点移动的距离相等
C. 经过旋转,图形的对应线段、对应角分别相等
D. 经过旋转,图形的对应点的连线平行且相等
2. 如图,在△ABC中,∠BAC=90°,将其绕点C逆时针旋转48°得到△A'B'C,点A在边B'C上,则∠B'的度数为 ( )
A. 42° B. 48°
C. 52° D. 58°
3. 如图,△ABC为直角三角形,∠ACB=90°,BC=3cm,AC=4cm,将△ABC绕点C逆时针旋转90°后得到△EDC,则∠B=∠ ,CE= cm,AD= cm,DE与AB的位置关系是 .
4. (2023·张家界)如图,AO为∠BAC的平分线,且∠BAC=50°,将四边形ABOC绕点A按逆时针方向旋转后,得到四边形AB'O'C',且∠OAC'=100°,则四边形ABOC旋转的角度为 .
5. 在如图所示的由相同小正方形组成的网格图中,点O和△ABC的三个顶点均在格点(网格线的交点)上,画出△ABC绕点O顺时针旋转90°后得到的△A1B1C1.
6. (2024·陕西改编)如图,在△AOB中,∠AOB=90°,将△AOB绕点O顺时针旋转45°,得到△A'OB',图中互相垂直的两条线段所在的直线有 ( )
A. 1组 B. 2组 C. 3组 D. 4组
7. 如图,在4×4的方格纸中,△MNP绕某点旋转一定的角度,得到△M1N1P1,则其旋转中心一定是点 .
8. 如图,教室里有一只倒地的簸箕,BC与地面的夹角为50°,∠DCB=25°,小明同学将它扶起平放在地面上(点C不动),则簸箕柄AB绕点C转动的角度为 .
9. 将一副三角尺按如图所示的方式叠放在一起,其中点B,D重合.若固定三角尺AOB,将三角尺ACD绕点A顺时针旋转一周,则当旋转的角度为 时,CD∥AO.
10. 如图,四边形ABCD绕点O旋转后,顶点A的对应点为E,试确定点B,C,D的对应点的位置,并画出旋转后的四边形.
11. 如图,在由边长均为1个单位长度的小正方形组成的网格中,△A'B'C'是由△ABC通过图形变换或变换组合(平移、轴对称、旋转)得到的,请你写出一种方案.
第11题
第3课时 中心对称与中心对称图形
1. (2024·德州)下列图形是中心对称图形的为 ( )
2. 若点M,N关于点O中心对称,则下列说法不正确的是 ( )
A. OM=ON B. 点M,O,N在同一条直线上
C. △OMN是等腰三角形 D. 线段OM绕点O旋转180°能与线段ON重合
3. 如图,△AOB与△DOC成中心对称,△AOB的面积是6,AB=3,则△DOC的边CD上的高是 .
4. (2024·牡丹江改编)如图所示为四个图形,其中图④是等腰三角形.
(1) 属于轴对称图形的有 (填序号),它们的对称轴分别有 条;
(2) 图①②分别至少旋转 °, °时,能与原图形互相重合;
(3) 属于中心对称图形的有 (填序号).
5. (1) 如图①所示为由边长为1的小等边三角形构成的网格,现有5个小等边三角形已涂上阴影,请在余下的空白小等边三角形中选取1个涂上阴影,使得6个阴影小等边三角形组成一个中心对称图形.
(2) 在如图②所示的网格中,选取2个空白小正方形涂上阴影,使6个阴影小正方形组成一个中心对称图形;在如图③所示的网格中,选取2个空白小正方形涂上阴影,使6个阴影小正方形组成一个轴对称图形,但不是中心对称图形.
6. 如图,△ABC与△A'B'C'关于点O成中心对称,则下列结论不一定成立的是 ( )
A. A'是点A关于点O的对称点 B. BO=B'O
C. AB∥A'B' D. ∠ABC=∠C'A'B'
7. 如图,直线a,b互相垂直且相交于点O,曲线C关于点O成中心对称,点A的对称点是A',AB⊥a于点B,A'D⊥b于点D.若OB=3,OD=2,则涂色部分的面积之和为 .
8. 如图所示为两张完全重合在一起的等边三角形硬纸片,点O是它们的中心.若按住下面的硬纸片不动,将上面的硬纸片绕点O按顺时针方向旋转,则旋转的角度至少为 时,两张硬纸片所构成的图形是中心对称图形.
9. 在正方形网格中,△ABC的顶点在格点上.请仅用无刻度的直尺完成以下作图.
(1) 如图①,作△ABC关于点O对称的△A'B'C';
(2) 如图②,作△ABC绕点A按顺时针方向旋转一定角度后,顶点仍在格点上的△AB'C'.
10. 如图,在△ABC中,D是边BC上的中点,连接AD.
(1) 画出与△ACD关于点D成中心对称的三角形;
(2) 在(1)的基础上找出与AC相等的线段;
(3) 在△ABC中,探索AB+AC与AD之间的数量关系,并说明理由.
第10题
9.2 轴 对 称
第1课时 轴对称的概念
1. C 2. C 3. 309087 4. 12
5. (1) 如图所示 (2) △A1B1C1的面积为3×5-×3×3-×2×2-×5×1=6 (3) 如图,四边形CAA1C1的面积为×(4+10)×3=21
6. 如图所示
第2课时 垂直平分线的概念及其作法
1. D 2. BD⊥AC 3. (1) 6 (2) △BOF (3) 30
4. (1) 如图,直线EF即为所求 (2) EC,CF,AF
5. (1) 如图,点D即为所求 (2) 如图,直线DE即为所求
第3课时 轴对称的基本性质
1. C 2. B 3. 4 4. 垂直平分线 平行
5. 如图所示 (1) 如图所示
(2) 10 解析:S△DEF=S△ABC=×5×4=10.
6. 如图所示
7. A 8. 书
9. 如图,线段M1N1和M2N2即为所求 不成
10. 如图,△EDC即为所求
11. (1) 如图,△ABC即为所求 (2) 如图,直线EF即为所求
(3) ∠BOB″=2∠α 解析:如图,连接BO,B'O,B″O.因为△ABC与△A'B'C'关于直线MN对称,所以∠BOM=∠B'OM.又因为△A'B'C'与△A″B″C″关于直线EF对称,所以∠B'OE=∠B″OE,所以∠BOB″=∠BOM+∠B'OM+∠B'OE+∠B″OE=2(∠B'OM+∠B'OE)=2∠MOE=2∠α.
第4课时 轴对称图形
1. A 2. C
3. ③ 8 ②⑥⑦⑧ 解析:如图,对称轴条数最多的是③,共有8条对称轴;只有1条对称轴的是②⑥⑦⑧.
① ② ③ ④
4. 如图①②③所示
5. 答案不唯一,如图所示
6. B 7. A或C
8. 4 解析:如图,涂灰①~④中任意一个均满足题意.
9. 三角形④分别与三角形②、三角形③成轴对称 整个图形是轴对称图形,它共有2条对称轴 如图,直线l1,l2就是整个图形的对称轴
10. 如图所示
9.3 旋 转
第1课时 旋转的概念
1. D 2. A 3. D 4. 4 5. (1) B (2) ∠BOD (3) BD (4) 60
6. (1) 如图,△A1B1C1即为所求 (2) 如图,△A2B1C2即为所求
7. C 8. D
9. 30°或150° 解析:当点D在点A的左侧时,∠BAE=30°;当点D在点A的右侧时,∠BAE=150°.
10. (1) 如图,△A1B1C1即为所求 (2) 以B,C1,B1,C为顶点的四边形的面积为10×8-2××2×4-2××4×8=40 (3) 如图,点E即为所求
11. 因为BC=2,BD∶CD=1∶3,所以BD=×BC=,DC=×BC=.因为将△ADC绕点A顺时针旋转90°得到△AEB,所以DC=EB=,∠ABE=∠C=45°.因为∠ABC=45°,所以∠EBD=90°,所以△BDE的面积为BD·EB=××=
第2课时 旋转的基本性质
1. C 2. A 3. EDC 4 1 垂直 4. 75°
5. 如图所示
6. D 7. B 8. 105°
9. 75°或255° 解析:如图①,当CD在OA的左侧,CD∥AO时,易得旋转的角度为45°+30°=75°;如图②,当CD在OA的右侧,CD∥OA时,易得旋转的角度为45°+180°+30°=255°.综上所述,当旋转的角度为75°或255°时,CD∥AO.
10. 如图,点B的对应点为F,点C的对应点为G,点D的对应点为H,四边形EFGH即为旋转后的四边形
11. 答案不唯一,如先将△ABC绕点A逆时针旋转90°,再向下平移2个单位长度,最后向右平移2个单位长度
第3课时 中心对称与中心对称图形
1. B 2. C 3. 4 4. (1) ①②③④ 4,3,2,1
(2) 90 120 (3) ①③
5. 答案不唯一,如(1) 如图①所示 (2) 如图②③所示
6. D 7. 6
8. 60° 解析:如图,至少旋转60°,两张硬纸片所构成的图形是中心对称图形.
9. (1) 如图①,△A'B'C'即为所求 (2) 如图②,△AB'C'即为所求
10. (1) 如图,延长AD至点A',使A'D=AD,连接A'B,则△A'BD就是与△ACD关于点D成中心对称的三角形 (2) A'B=AC (3) AB+AC>2AD 理由:因为△ACD与△A'BD关于点D成中心对称,所以AD=A'D,AC=A'B.在△ABA'中,根据两点之间,线段最短,得AB+A'B>AA',所以AB+AC>AD+A'D,即AB+AC>2AD.
同课章节目录
- 第7章 平面图形的认识(二)
- 7.1 探索直线平行的条件
- 7.2 探索平行线的性质
- 7.3 图形的平移
- 7.4 认识三角形
- 7.5 多边形的内角和与外角和
- 第8章 幂的运算
- 8.1 同底数幂的乘法
- 8.2 幂的乘方与积的乘方
- 8.3 同底数幂的除法
- 第9章 整式乘法与因式分解
- 9.1 单项式乘单项式
- 9.2 单项式乘多项式
- 9.3 多项式乘多项式
- 9.4 乘法公式
- 9.5 多项式的因式分解
- 第10章 二元一次方程组
- 10.1 二元一次方程
- 10.2 二元一次方程组
- 10.3 解二元一次方程组
- 10.4 三元一次方程组
- 10.5 用二元一次方程解决问题
- 第11章 一元一次不等式
- 11.1 生活中的不等式
- 11.2 不等式的解集
- 11.3 不等式的性质
- 11.4 解一元一次不等式
- 11.5 用一元一次不等式解决问题
- 11.6 一元一次不等式组
- 第12章 证明
- 12.1 定义与命题
- 12.2 证明
- 12.3 互逆命题
