第12章定义命题证明 同步练 (含答案)2024-2025学年数学苏科版七年级下册
文档属性
| 名称 | 第12章定义命题证明 同步练 (含答案)2024-2025学年数学苏科版七年级下册 |

|
|
| 格式 | docx | ||
| 文件大小 | 194.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-03-29 22:24:45 | ||
图片预览

文档简介
第12章 定义 命题 证明
考点一 定义与命题
1. 下列句子中,属于定义的是 ( )
A. 多边形相邻两边组成的角叫作多边形的内角
B. 五边形的外角和为360°
C. 两点之间,线段最短
D. 在△ABC中,若∠A∶∠B∶∠C=3∶4∶5,则△ABC是直角三角形
2. 下列语句中,属于命题的是 ( )
A. ∠1=∠2吗 B. 过点A作直线MN C. 同角的余角相等 D. 取线段AB的中点
3. 下列说法中,正确的是 ( )
A. 每个定理的逆命题均为真命题 B. 每个命题都有逆命题
C. 假命题的逆命题一定是假命题 D. 真命题的逆命题一定是真命题
4. (1) (2024·无锡)命题“若a>b,则a-3(2) 改写命题“等角的补角相等”:如果 ,那么 .
5. 如图,∠B+∠D=∠BED.
(1) 求证:AB∥CD.
(2) 在(1)的证明过程中,有没有运用到互逆的真命题 若有,请指出来.
第5题
考点二 三角形内角和定理及其推论
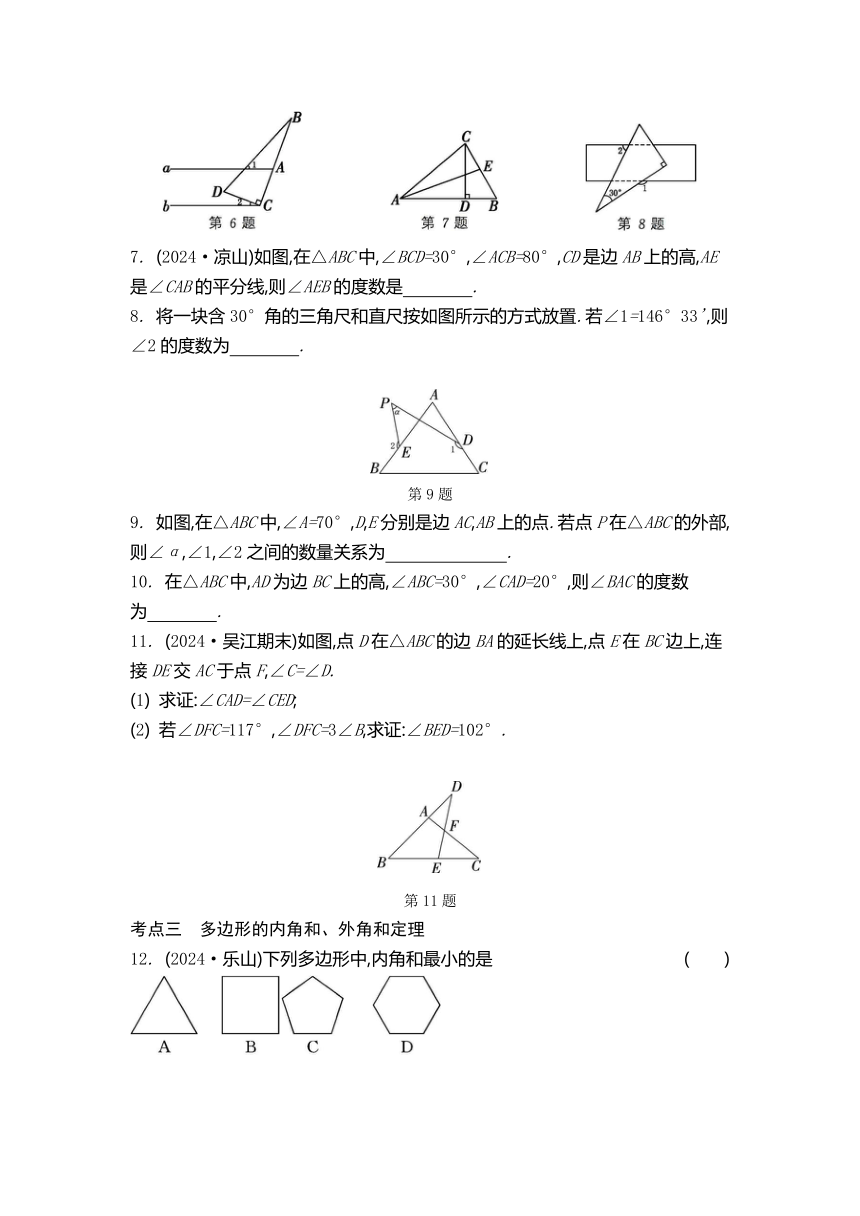
6. 如图,直线a∥b,将△BCD按如图所示的方式放置,其中∠DCB=90°.若∠1+∠B=70°,则∠2的度数为 ( )
A. 20° B. 40° C. 30° D. 25°
7. (2024·凉山)如图,在△ABC中,∠BCD=30°,∠ACB=80°,CD是边AB上的高,AE是∠CAB的平分线,则∠AEB的度数是 .
8. 将一块含30°角的三角尺和直尺按如图所示的方式放置.若∠1=146°33',则∠2的度数为 .
第9题
9. 如图,在△ABC中,∠A=70°,D,E分别是边AC,AB上的点.若点P在△ABC的外部,则∠α,∠1,∠2之间的数量关系为 .
10. 在△ABC中,AD为边BC上的高,∠ABC=30°,∠CAD=20°,则∠BAC的度数为 .
11. (2024·吴江期末)如图,点D在△ABC的边BA的延长线上,点E在BC边上,连接DE交AC于点F,∠C=∠D.
(1) 求证:∠CAD=∠CED;
(2) 若∠DFC=117°,∠DFC=3∠B,求证:∠BED=102°.
第11题
考点三 多边形的内角和、外角和定理
12. (2024·乐山)下列多边形中,内角和最小的是 ( )
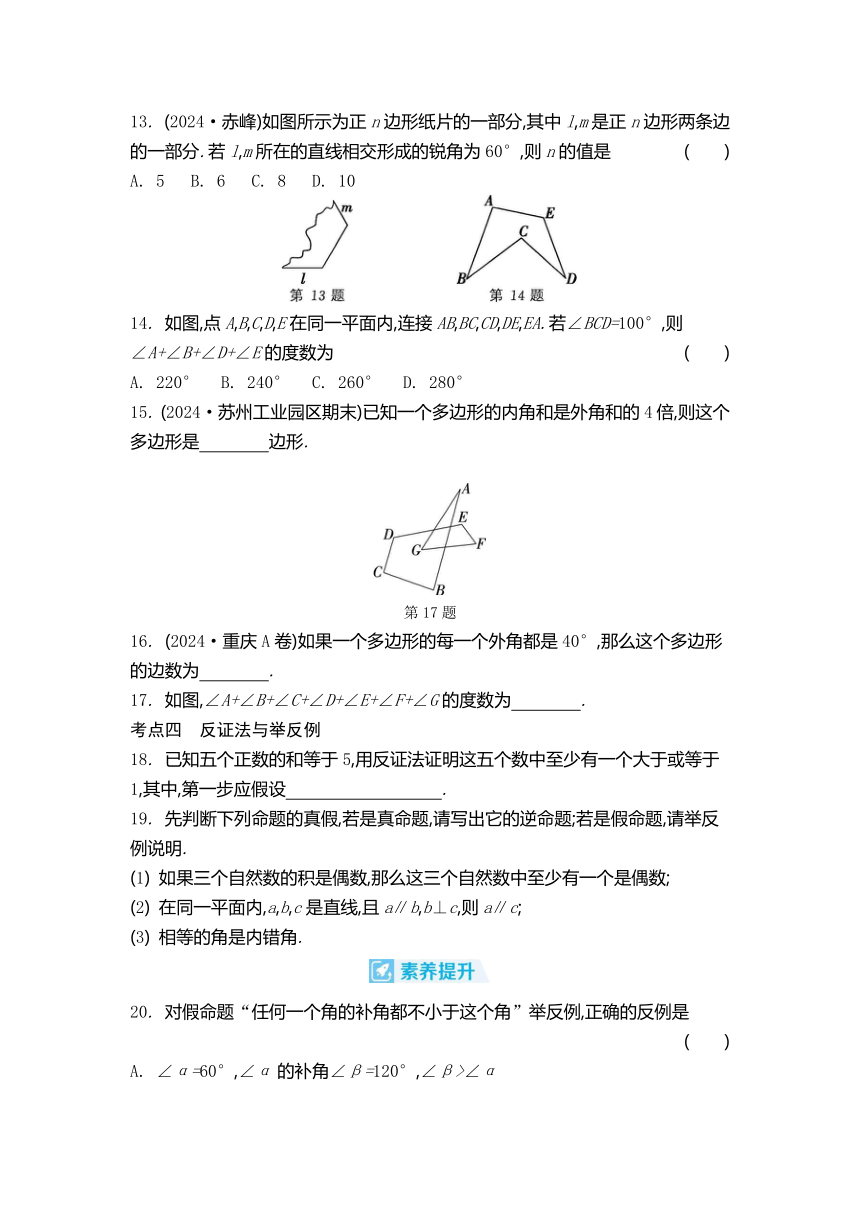
13. (2024·赤峰)如图所示为正n边形纸片的一部分,其中l,m是正n边形两条边的一部分.若l,m所在的直线相交形成的锐角为60°,则n的值是 ( )
A. 5 B. 6 C. 8 D. 10
14. 如图,点A,B,C,D,E在同一平面内,连接AB,BC,CD,DE,EA.若∠BCD=100°,则∠A+∠B+∠D+∠E的度数为 ( )
A. 220° B. 240° C. 260° D. 280°
15. (2024·苏州工业园区期末)已知一个多边形的内角和是外角和的4倍,则这个多边形是 边形.
第17题
16. (2024·重庆A卷)如果一个多边形的每一个外角都是40°,那么这个多边形的边数为 .
17. 如图,∠A+∠B+∠C+∠D+∠E+∠F+∠G的度数为 .
考点四 反证法与举反例
18. 已知五个正数的和等于5,用反证法证明这五个数中至少有一个大于或等于1,其中,第一步应假设 .
19. 先判断下列命题的真假,若是真命题,请写出它的逆命题;若是假命题,请举反例说明.
(1) 如果三个自然数的积是偶数,那么这三个自然数中至少有一个是偶数;
(2) 在同一平面内,a,b,c是直线,且a∥b,b⊥c,则a∥c;
(3) 相等的角是内错角.
20. 对假命题“任何一个角的补角都不小于这个角”举反例,正确的反例是 ( )
A. ∠α=60°,∠α的补角∠β=120°,∠β>∠α
B. ∠α=90°,∠α的补角∠β=90°,∠β=∠α
C. ∠α=100°,∠α的补角∠β=80°,∠β<∠α
D. 互补的两个角有一条公共边
21. 如图,D为△ABC边BC的延长线上一点.若∠A∶∠ABC=3∶4,∠ACD=140°,∠ABC的平分线与∠ACD的平分线交于点M,则∠M= °.
22. (2024·苏州期中)如图,在三角形纸片ABC中,∠A=58°,∠B=83°,将纸片的一角折叠,使点C落在△ABC内.若∠1=38°,则∠2的度数为 .
23. (2023·苏州市区期中)如图所示为可调躺椅示意图,AE与BD的交点为C,且∠A,∠B,∠E保持不变.为了舒适,需调整∠D的大小,使∠EFD=110°,则图中∠D应 (填“增加”或“减少”) .
24. (2024·苏州期中)在平面内有n个点,其中每三个点都能构成等腰三角形,我们把具有这样性质的n个点构成的点集称为“爱尔特希点集”.如图,四边形ABCD的四个顶点构成“爱尔特希点集”.若平面内存在一个点P与A,B,C,D四个点也构成“爱尔特希点集”,则∠APB的度数为 .
25. (2023·苏州市区期中)如图,AB∥EF,∠BAC与∠CDE的平分线交于点G,且GF∥DE,已知∠ACD=90°,若∠AGD=α,∠GFE=β,则α与β的数量关系为 .
26. 在△ABC中,D为边BC上一点,请回答下列问题:
(1) 如图①,∠B=∠DAC,CE平分∠ACB,交AD于点F,交AB于点E.求证:∠AEF=∠AFE.
(2) 在(1)的条件下,如图②,△ABC的外角∠ACQ的平分线CP交BA的延长线于点P,则∠P与∠CFD之间有怎样的数量关系 请给出证明.
(3) 如图③,点P在BA的延长线上,PD交AC于点F,且∠B=∠CFD,PE平分∠BPD,过点C作CE⊥PE,垂足为E,交PD于点G.求证:CE平分∠ACB.
第12章 定义 命题 证明
1. A 2. C 3. B 4. (1) 假 (2) 两个角相等 这两个角的补角相等
5. (1) 过点E作EF∥AB(点F在点E的右侧),则∠B=∠BEF.∵ ∠B+∠D=∠BED,∠BEF+∠DEF=∠BED,∴ ∠D=∠DEF,∴ EF∥CD,∴ AB∥CD (2) 有 运用了“两直线平行,内错角相等”和“内错角相等,两直线平行”这两个互逆的真命题
6. A 7. 100° 8. 63°27' 9. ∠2-∠1=∠α-70° 10. 80°或40°
11. (1) ∵ ∠CAD是△ABC的外角,∴ ∠CAD=∠B+∠C.∵ ∠CED是△BDE的外角,∴ ∠CED=∠B+∠D.∵ ∠C=∠D,∴ ∠CAD=∠CED (2) 设∠D=x,则∠C=x.∵ ∠DFC=117°,∠DFC=3∠B,∴ ∠B=∠DFC=×117°=39°.∵ ∠CFE+∠DFC=180°,∴ ∠CFE=180°-117°=63°.由(1),得∠CED=∠B+∠D=39°+x.∵ △CEF的内角和为180°,∴ ∠C+∠CFE+∠CED=180°,∴ x+63°+(39°+x)=180°,解得x=39°,即∠C=39°.∵ ∠BED是△CEF的外角,∴ ∠BED=∠CFE+∠C=63°+39°=102°
12. A 13. B 14. D 15. 十 16. 9
17. 540° 解析:连接BF,则∠A+∠G=∠ABF+∠GFB,从而将题中待求角度的和转化为五边形DCBFE的内角和.
18. 这五个正数都小于1
19. (1) 真命题 逆命题:如果三个自然数中至少有一个是偶数,那么这三个自然数的积是偶数 (2) 假命题 如图①,满足a∥b,b⊥c,但a与c不平行,∴ 该命题为假命题 (3) 假命题 反例不唯一,如图②,直线a与b相交于点O,∠1=∠2(对顶角相等),但∠1与∠2不是内错角,∴ 该命题为假命题
20. C 21. 30 22. 40° 23. 减少 10°
24. 72°或36° 解析:由题意,知当A,B,C,D四个点为某正五边形的四个顶点时,构成“爱尔特希点集”.当点P为正五边形的中心时,与A,B,C,D四个点构成“爱尔特希点集”,此时∠APB=72°;当点P在正五边形的顶点处(除A,B,C,D四个顶点外的另一个顶点)时,∠APB=36°.综上所述,∠APB的度数为72°或36°.
25. 2α+β=90° 解析:如图,过点D作DP∥EF,连接GC并延长至点H.∵ AB∥EF,∴ AB∥DP,∴ 易得∠ACD=∠BAC+∠PDC=90°.∵ ∠ACH是△ACG的外角,∠DCH是△DCG的外角,∴ ∠ACD=∠CAG+∠CDG+∠AGD,∴ ∠CAG+∠CDG=90°-α.∵ ∠BAC与∠CDE的平分线交于点G,∴ ∠BAC=2∠GAC,∠CDG=∠EDG,∴ 2∠GAC+∠CDG+(∠EDG-∠EDP)=90°.∵ DP∥EF,DE∥GF,∴ 易得∠EDP=∠F=β,∴ 2∠GAC+∠CDG+(∠EDG-β)=90°,即2∠GAC+2∠CDG-β=90°,∴ 2(90°-α)-β=90°,化简,得2α+β=90°.
26. (1) ∵ CE平分∠ACB,∴ ∠ECB=∠ACE.又∵ ∠AEF=∠B+∠ECB,∠AFE=∠FAC+∠ACE,∠B=∠FAC,∴ ∠AEF=∠AFE (2) ∠P+∠CFD=90° ∵ CP是∠ACQ的平分线,∴ ∠ACP=∠ACQ.∵ ∠ACE=∠ACB,∴ ∠ECP=∠ACE+∠ACP=(∠ACB+∠ACQ)=90°,∴ ∠P+∠AEC=90°.∵ ∠AEF=∠AFE,∠AFE=∠CFD,∴ ∠AEF=∠CFD,∴ ∠P+∠CFD=90° (3) 延长PE交BC于点H,设PE交AC于点K.∵ PE平分∠BPD,∴ ∠BPK=∠KPF.又∵ ∠EKC=∠KPF+∠PFA,∠EHC=∠B+∠BPK,∠B=∠CFD=∠PFA,∴ ∠EKC=∠EHC.∵ CE⊥KH,∴ ∠CEK=∠CEH=90°,∴ ∠EKC+∠ECK=90°,∠EHC+∠ECH=90°,∴ ∠ECK=∠ECH,∴ CE平分∠ACB
考点一 定义与命题
1. 下列句子中,属于定义的是 ( )
A. 多边形相邻两边组成的角叫作多边形的内角
B. 五边形的外角和为360°
C. 两点之间,线段最短
D. 在△ABC中,若∠A∶∠B∶∠C=3∶4∶5,则△ABC是直角三角形
2. 下列语句中,属于命题的是 ( )
A. ∠1=∠2吗 B. 过点A作直线MN C. 同角的余角相等 D. 取线段AB的中点
3. 下列说法中,正确的是 ( )
A. 每个定理的逆命题均为真命题 B. 每个命题都有逆命题
C. 假命题的逆命题一定是假命题 D. 真命题的逆命题一定是真命题
4. (1) (2024·无锡)命题“若a>b,则a-3
5. 如图,∠B+∠D=∠BED.
(1) 求证:AB∥CD.
(2) 在(1)的证明过程中,有没有运用到互逆的真命题 若有,请指出来.
第5题
考点二 三角形内角和定理及其推论
6. 如图,直线a∥b,将△BCD按如图所示的方式放置,其中∠DCB=90°.若∠1+∠B=70°,则∠2的度数为 ( )
A. 20° B. 40° C. 30° D. 25°
7. (2024·凉山)如图,在△ABC中,∠BCD=30°,∠ACB=80°,CD是边AB上的高,AE是∠CAB的平分线,则∠AEB的度数是 .
8. 将一块含30°角的三角尺和直尺按如图所示的方式放置.若∠1=146°33',则∠2的度数为 .
第9题
9. 如图,在△ABC中,∠A=70°,D,E分别是边AC,AB上的点.若点P在△ABC的外部,则∠α,∠1,∠2之间的数量关系为 .
10. 在△ABC中,AD为边BC上的高,∠ABC=30°,∠CAD=20°,则∠BAC的度数为 .
11. (2024·吴江期末)如图,点D在△ABC的边BA的延长线上,点E在BC边上,连接DE交AC于点F,∠C=∠D.
(1) 求证:∠CAD=∠CED;
(2) 若∠DFC=117°,∠DFC=3∠B,求证:∠BED=102°.
第11题
考点三 多边形的内角和、外角和定理
12. (2024·乐山)下列多边形中,内角和最小的是 ( )
13. (2024·赤峰)如图所示为正n边形纸片的一部分,其中l,m是正n边形两条边的一部分.若l,m所在的直线相交形成的锐角为60°,则n的值是 ( )
A. 5 B. 6 C. 8 D. 10
14. 如图,点A,B,C,D,E在同一平面内,连接AB,BC,CD,DE,EA.若∠BCD=100°,则∠A+∠B+∠D+∠E的度数为 ( )
A. 220° B. 240° C. 260° D. 280°
15. (2024·苏州工业园区期末)已知一个多边形的内角和是外角和的4倍,则这个多边形是 边形.
第17题
16. (2024·重庆A卷)如果一个多边形的每一个外角都是40°,那么这个多边形的边数为 .
17. 如图,∠A+∠B+∠C+∠D+∠E+∠F+∠G的度数为 .
考点四 反证法与举反例
18. 已知五个正数的和等于5,用反证法证明这五个数中至少有一个大于或等于1,其中,第一步应假设 .
19. 先判断下列命题的真假,若是真命题,请写出它的逆命题;若是假命题,请举反例说明.
(1) 如果三个自然数的积是偶数,那么这三个自然数中至少有一个是偶数;
(2) 在同一平面内,a,b,c是直线,且a∥b,b⊥c,则a∥c;
(3) 相等的角是内错角.
20. 对假命题“任何一个角的补角都不小于这个角”举反例,正确的反例是 ( )
A. ∠α=60°,∠α的补角∠β=120°,∠β>∠α
B. ∠α=90°,∠α的补角∠β=90°,∠β=∠α
C. ∠α=100°,∠α的补角∠β=80°,∠β<∠α
D. 互补的两个角有一条公共边
21. 如图,D为△ABC边BC的延长线上一点.若∠A∶∠ABC=3∶4,∠ACD=140°,∠ABC的平分线与∠ACD的平分线交于点M,则∠M= °.
22. (2024·苏州期中)如图,在三角形纸片ABC中,∠A=58°,∠B=83°,将纸片的一角折叠,使点C落在△ABC内.若∠1=38°,则∠2的度数为 .
23. (2023·苏州市区期中)如图所示为可调躺椅示意图,AE与BD的交点为C,且∠A,∠B,∠E保持不变.为了舒适,需调整∠D的大小,使∠EFD=110°,则图中∠D应 (填“增加”或“减少”) .
24. (2024·苏州期中)在平面内有n个点,其中每三个点都能构成等腰三角形,我们把具有这样性质的n个点构成的点集称为“爱尔特希点集”.如图,四边形ABCD的四个顶点构成“爱尔特希点集”.若平面内存在一个点P与A,B,C,D四个点也构成“爱尔特希点集”,则∠APB的度数为 .
25. (2023·苏州市区期中)如图,AB∥EF,∠BAC与∠CDE的平分线交于点G,且GF∥DE,已知∠ACD=90°,若∠AGD=α,∠GFE=β,则α与β的数量关系为 .
26. 在△ABC中,D为边BC上一点,请回答下列问题:
(1) 如图①,∠B=∠DAC,CE平分∠ACB,交AD于点F,交AB于点E.求证:∠AEF=∠AFE.
(2) 在(1)的条件下,如图②,△ABC的外角∠ACQ的平分线CP交BA的延长线于点P,则∠P与∠CFD之间有怎样的数量关系 请给出证明.
(3) 如图③,点P在BA的延长线上,PD交AC于点F,且∠B=∠CFD,PE平分∠BPD,过点C作CE⊥PE,垂足为E,交PD于点G.求证:CE平分∠ACB.
第12章 定义 命题 证明
1. A 2. C 3. B 4. (1) 假 (2) 两个角相等 这两个角的补角相等
5. (1) 过点E作EF∥AB(点F在点E的右侧),则∠B=∠BEF.∵ ∠B+∠D=∠BED,∠BEF+∠DEF=∠BED,∴ ∠D=∠DEF,∴ EF∥CD,∴ AB∥CD (2) 有 运用了“两直线平行,内错角相等”和“内错角相等,两直线平行”这两个互逆的真命题
6. A 7. 100° 8. 63°27' 9. ∠2-∠1=∠α-70° 10. 80°或40°
11. (1) ∵ ∠CAD是△ABC的外角,∴ ∠CAD=∠B+∠C.∵ ∠CED是△BDE的外角,∴ ∠CED=∠B+∠D.∵ ∠C=∠D,∴ ∠CAD=∠CED (2) 设∠D=x,则∠C=x.∵ ∠DFC=117°,∠DFC=3∠B,∴ ∠B=∠DFC=×117°=39°.∵ ∠CFE+∠DFC=180°,∴ ∠CFE=180°-117°=63°.由(1),得∠CED=∠B+∠D=39°+x.∵ △CEF的内角和为180°,∴ ∠C+∠CFE+∠CED=180°,∴ x+63°+(39°+x)=180°,解得x=39°,即∠C=39°.∵ ∠BED是△CEF的外角,∴ ∠BED=∠CFE+∠C=63°+39°=102°
12. A 13. B 14. D 15. 十 16. 9
17. 540° 解析:连接BF,则∠A+∠G=∠ABF+∠GFB,从而将题中待求角度的和转化为五边形DCBFE的内角和.
18. 这五个正数都小于1
19. (1) 真命题 逆命题:如果三个自然数中至少有一个是偶数,那么这三个自然数的积是偶数 (2) 假命题 如图①,满足a∥b,b⊥c,但a与c不平行,∴ 该命题为假命题 (3) 假命题 反例不唯一,如图②,直线a与b相交于点O,∠1=∠2(对顶角相等),但∠1与∠2不是内错角,∴ 该命题为假命题
20. C 21. 30 22. 40° 23. 减少 10°
24. 72°或36° 解析:由题意,知当A,B,C,D四个点为某正五边形的四个顶点时,构成“爱尔特希点集”.当点P为正五边形的中心时,与A,B,C,D四个点构成“爱尔特希点集”,此时∠APB=72°;当点P在正五边形的顶点处(除A,B,C,D四个顶点外的另一个顶点)时,∠APB=36°.综上所述,∠APB的度数为72°或36°.
25. 2α+β=90° 解析:如图,过点D作DP∥EF,连接GC并延长至点H.∵ AB∥EF,∴ AB∥DP,∴ 易得∠ACD=∠BAC+∠PDC=90°.∵ ∠ACH是△ACG的外角,∠DCH是△DCG的外角,∴ ∠ACD=∠CAG+∠CDG+∠AGD,∴ ∠CAG+∠CDG=90°-α.∵ ∠BAC与∠CDE的平分线交于点G,∴ ∠BAC=2∠GAC,∠CDG=∠EDG,∴ 2∠GAC+∠CDG+(∠EDG-∠EDP)=90°.∵ DP∥EF,DE∥GF,∴ 易得∠EDP=∠F=β,∴ 2∠GAC+∠CDG+(∠EDG-β)=90°,即2∠GAC+2∠CDG-β=90°,∴ 2(90°-α)-β=90°,化简,得2α+β=90°.
26. (1) ∵ CE平分∠ACB,∴ ∠ECB=∠ACE.又∵ ∠AEF=∠B+∠ECB,∠AFE=∠FAC+∠ACE,∠B=∠FAC,∴ ∠AEF=∠AFE (2) ∠P+∠CFD=90° ∵ CP是∠ACQ的平分线,∴ ∠ACP=∠ACQ.∵ ∠ACE=∠ACB,∴ ∠ECP=∠ACE+∠ACP=(∠ACB+∠ACQ)=90°,∴ ∠P+∠AEC=90°.∵ ∠AEF=∠AFE,∠AFE=∠CFD,∴ ∠AEF=∠CFD,∴ ∠P+∠CFD=90° (3) 延长PE交BC于点H,设PE交AC于点K.∵ PE平分∠BPD,∴ ∠BPK=∠KPF.又∵ ∠EKC=∠KPF+∠PFA,∠EHC=∠B+∠BPK,∠B=∠CFD=∠PFA,∴ ∠EKC=∠EHC.∵ CE⊥KH,∴ ∠CEK=∠CEH=90°,∴ ∠EKC+∠ECK=90°,∠EHC+∠ECH=90°,∴ ∠ECK=∠ECH,∴ CE平分∠ACB
同课章节目录
- 第7章 平面图形的认识(二)
- 7.1 探索直线平行的条件
- 7.2 探索平行线的性质
- 7.3 图形的平移
- 7.4 认识三角形
- 7.5 多边形的内角和与外角和
- 第8章 幂的运算
- 8.1 同底数幂的乘法
- 8.2 幂的乘方与积的乘方
- 8.3 同底数幂的除法
- 第9章 整式乘法与因式分解
- 9.1 单项式乘单项式
- 9.2 单项式乘多项式
- 9.3 多项式乘多项式
- 9.4 乘法公式
- 9.5 多项式的因式分解
- 第10章 二元一次方程组
- 10.1 二元一次方程
- 10.2 二元一次方程组
- 10.3 解二元一次方程组
- 10.4 三元一次方程组
- 10.5 用二元一次方程解决问题
- 第11章 一元一次不等式
- 11.1 生活中的不等式
- 11.2 不等式的解集
- 11.3 不等式的性质
- 11.4 解一元一次不等式
- 11.5 用一元一次不等式解决问题
- 11.6 一元一次不等式组
- 第12章 证明
- 12.1 定义与命题
- 12.2 证明
- 12.3 互逆命题
