第12章定义命题证明 单元测试(含答案) 2024-2025学年数学苏科版七年级下册
文档属性
| 名称 | 第12章定义命题证明 单元测试(含答案) 2024-2025学年数学苏科版七年级下册 |

|
|
| 格式 | docx | ||
| 文件大小 | 189.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-03-29 22:31:07 | ||
图片预览


文档简介
第12章定义命题证明
时间:60分钟
一、 选择题(每小题3分,共24分)
1. 下列语句中,不属于命题的是 ( )
A. 延长线段AB到点C B. 自然数都是整数
C. 有两条边相等的三角形是等腰三角形 D. 平行于同一条直线的两条直线平行
2. 如图,∠A的两条边被一条直线所截,用含α和β的式子表示∠A为 ( )
A. α-β B. β-α
C. 180°-α+β D. 180°-α-β
3. 如图,∠ACB=90°,CD⊥AB,垂足为D,则下列结论错误的是 ( )
A. 图中有三个直角三角形 B. ∠1=∠2
C. ∠1和∠B都是∠A的余角 D. ∠2=∠A
4. 下列命题中,属于真命题的是 ( )
A. 锐角小于它的余角 B. 锐角小于它的补角
C. 锐角与锐角的和是钝角 D. 锐角与钝角的和等于平角
5. 游戏中有数学智慧,找起点游戏规定:从起点走五段相等直路之后回到起点,要求每走完一段直路后向右边偏行.成功的招数不止一招,可助我们成功的一招是 ( )
A. 每走完一段直路后沿向右偏72°方向行走 B. 每段直路要短
C. 每走完一段直路后沿向右偏108°方向行走 D. 每段直路要长
6. 能说明“锐角α、锐角β的和是锐角”是假命题的例证图是 ( )
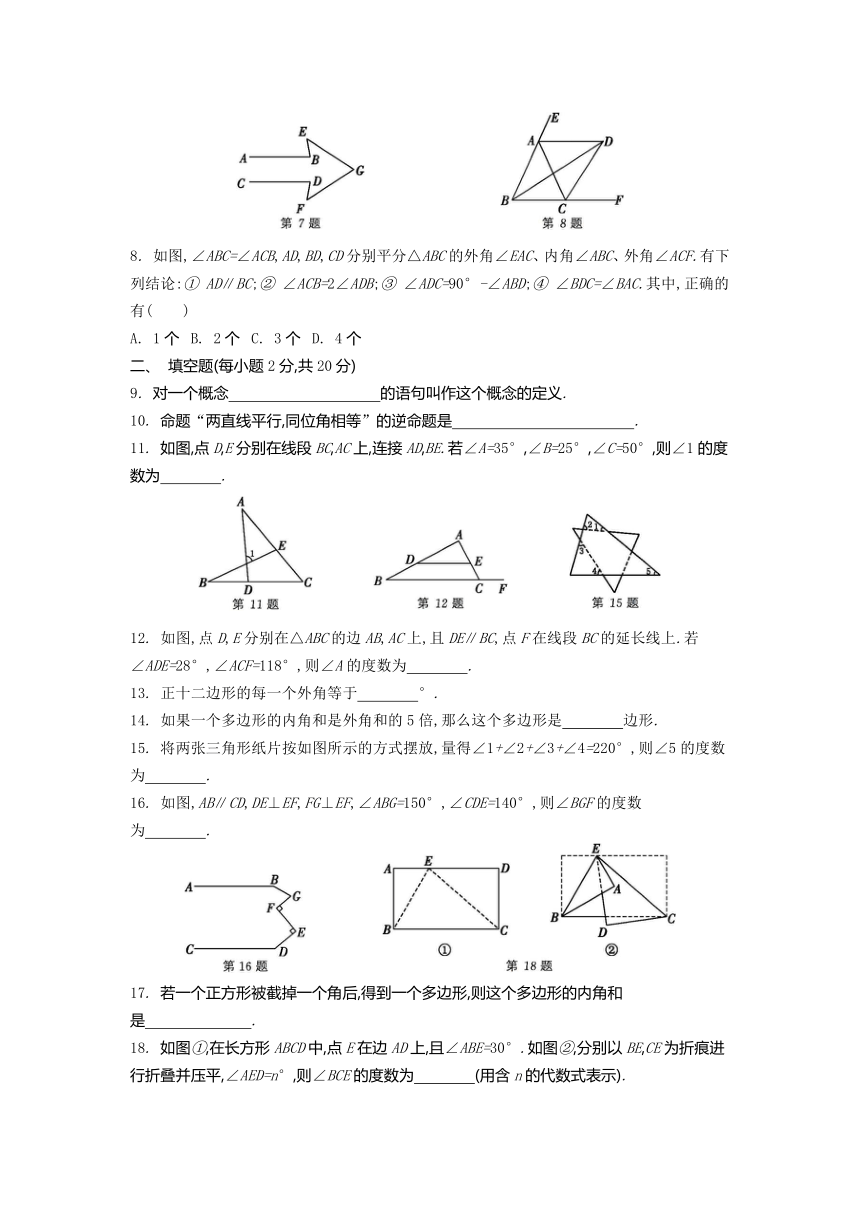
7. 在如图所示的“箭头”图形中,AB∥CD,∠ABE=∠CDF=80°,∠E=∠F=47°,则∠G的度数是 ( )
A. 80° B. 76° C. 66° D. 56°
8. 如图,∠ABC=∠ACB,AD,BD,CD分别平分△ABC的外角∠EAC、内角∠ABC、外角∠ACF.有下列结论:① AD∥BC;② ∠ACB=2∠ADB;③ ∠ADC=90°-∠ABD;④ ∠BDC=∠BAC.其中,正确的有( )
A. 1个 B. 2个 C. 3个 D. 4个
二、 填空题(每小题2分,共20分)
9. 对一个概念 的语句叫作这个概念的定义.
10. 命题“两直线平行,同位角相等”的逆命题是 .
11. 如图,点D,E分别在线段BC,AC上,连接AD,BE.若∠A=35°,∠B=25°,∠C=50°,则∠1的度数为 .
12. 如图,点D,E分别在△ABC的边AB,AC上,且DE∥BC,点F在线段BC的延长线上.若∠ADE=28°,∠ACF=118°,则∠A的度数为 .
13. 正十二边形的每一个外角等于 °.
14. 如果一个多边形的内角和是外角和的5倍,那么这个多边形是 边形.
15. 将两张三角形纸片按如图所示的方式摆放,量得∠1+∠2+∠3+∠4=220°,则∠5的度数为 .
16. 如图,AB∥CD,DE⊥EF,FG⊥EF,∠ABG=150°,∠CDE=140°,则∠BGF的度数为 .
17. 若一个正方形被截掉一个角后,得到一个多边形,则这个多边形的内角和是 .
18. 如图①,在长方形ABCD中,点E在边AD上,且∠ABE=30°.如图②,分别以BE,CE为折痕进行折叠并压平,∠AED=n°,则∠BCE的度数为 (用含n的代数式表示).
三、 解答题(共56分)
19. (6分)已知命题“如果a>1,那么a2>1”.
(1) 写出这个命题的逆命题;
(2) 举反例说明(1)中得到的逆命题是假命题.
20. (10分)如图,在△ABC中,AC⊥BC,DG⊥BC于点G,EF⊥AB于点E,∠1=∠2.求证:CD⊥AB.
第20题
证明:∵ DG⊥BC,AC⊥BC(已知),
∴ ∠DGB=∠ACB=90°(垂直的定义),
∴ DG∥AC( ),
∴ ∠2= ( ).
∵ ∠1=∠2(已知),
∴ ∠1= (等量代换),
∴ EF∥CD( ),
∴ ∠AEF= ( ).
∵ EF⊥AB(已知),
∴ ∠AEF=90°( ),
∴ ∠ADC=90°( ),
∴ CD⊥AB( ).
21. (10分)如图,在△ABC中,AD⊥BC于点D,BF平分∠ABC交AC于点F,交AD于点E.若∠AEF=∠AFB,试猜想△ABC的形状,并证明你的结论.
第21题
22. (10分)如图,如果直线AB,CD被直线EF所截,EF分别交AB,CD于点O,O',AB∥CD.请用反证法求证:∠EOB=∠EO'D.
第22题
23. (10分)研究一个问题:多边形的一个外角与它不相邻的内角之和具有怎样的数量关系
【探究1】 如图①,请直接写出∠ACD与∠A,∠B之间的数量关系: .
【探究2】 如图②,∠DCE是四边形ABCD的一个外角.求证:∠DCE=∠A+∠B+∠D-180°.
【结论】 若n边形的某一个外角的度数为x°,与这个外角不相邻的内角之和为y°,则x,y与n之间的数量关系为 .
24. (10分)已知∠MON=40°,OE平分∠MON,A,B,C分别是射线OM,OE,ON上的动点(点A,B,C不与点O重合),连接AB,AC,AC交射线OE于点D,设∠BAC=α.
(1) 如图①,若AB∥ON.
① ∠ABO的度数是 .
② 当∠BAD=∠ABD时,∠OAC的度数是 ;当∠BAD=∠BDA时,∠OAC的度数是 .
(2) 在一个四边形中,若存在一个内角是它的对角的2倍,我们称这样的四边形为“完美四边形”.如图②,若AB⊥OM,延长AB交射线ON于点F,当四边形DCFB为“完美四边形”时,求α.
第12章素能测评
一、 1. A 2. B 3. B 4. B 5. A 6. C
7. C 解析:延长AB交EG于点M,延长CD交FG于点N,过点G向左作GK∥AB,得∠KGM=∠EMB.结合AB∥CD,得GK∥CD,从而∠KGN=∠DNF,∴ ∠EGF=∠EMB+∠DNF.由三角形内角和定理的推论可求得∠EMB=33°,∠DNF=33°,∴ ∠EGF=∠EMB+∠DNF=33°+33°=66°.
8. C 解析:① 由AD平分△ABC的外角∠EAC,得∠EAD=∠DAC.由三角形内角和定理的推论,得∠EAC=∠ACB+∠ABC.结合∠ABC=∠ACB,得∠EAD=∠ABC.利用“同位角相等,两直线平行”得AD∥BC.故①正确.② 由AD∥BC,得∠ADB=∠DBC.由BD平分∠ABC,得∠ABD=∠DBC.∴ ∠ABC=2∠ADB,∴ ∠ACB=2∠ADB.故②正确.③ 在△ADC中,∠ADC+∠CAD+∠ACD=180°,利用角的关系,易得∠ADC+∠CAD+∠ACD=∠ADC+2∠ABD+∠ADC=2∠ADC+2∠ABD=180°,∴ ∠ADC=90°-∠ABD.故③正确.④ 由∠BAC+∠ABC=∠ACF,得∠BAC+∠ABC=∠ACF.结合∠BDC+∠DBC=∠ACF,得∠BAC=∠BDC.故④错误.
二、 9. 作出明确规定 10. 同位角相等,两直线平行 11. 70° 12. 90° 13. 30 14. 十二 15. 40° 16. 70° 17. 180°或360°或540° 18. °
三、 19. (1) 如果a2>1,那么a>1 (2) 举反例不唯一,如当a=-2时,a2=4>1,但a<1,故逆命题是假命题
20. 同位角相等,两直线平行 ∠ACD 两直线平行,内错角相等 ∠ACD 同位角相等,两直线平行 ∠ADC 两直线平行,同位角相等 垂直的定义 等量代换 垂直的定义
21. △ABC为直角三角形 ∵ BF平分∠ABC,∴ ∠ABF=∠EBD.∵ AD⊥BC,∴ 在△BDE中,∠EBD+∠BED=90°.∵ ∠AEF=∠BED,∴ ∠ABF+∠AEF=90°.∵ ∠AEF=∠AFB,∴ ∠ABF+∠AFB=90°,∴ ∠BAF=90°,∴ △ABC为直角三角形
22. 假设∠EOB≠∠EO'D.如图,过点O作直线A'B',使∠EOB'=∠EO'D.∴ A'B'∥CD.∵ AB∥CD,∴ 过点O有两条直线AB,A'B'都平行于直线CD.这与基本事实“过直线外一点有且只有一条直线与这条直线平行”矛盾.∴ 假设∠EOB≠∠EO'D不成立,∴ ∠EOB=∠EO'D
23. 【探究1】 ∠ACD=∠A+∠B 【探究2】 ∵ ∠A+∠B+∠D+∠BCD=360°,∠DCE+∠BCD=180°,∴ ∠BCD=360°-(∠A+∠B+∠D),∠BCD=180°-∠DCE,∴ 360°-(∠A+∠B+∠D)=180°-∠DCE,即∠DCE=∠A+∠B+∠D-180°
【结论】 y-x=180(n-3) 解析:∵ n边形的某一个外角的度数是x°,∴ 与这个外角相邻的内角的度数是(180-x)°.∵ 与这个外角不相邻的所有内角之和是y°,∴ (180-x)+y=(n-2)·180,整理,得y-x=180(n-3).
24. (1) ① 20° ② 120° 60° (2) ∵ OE平分∠MON,∠MON=40°,∴ ∠MOE=∠NOE=∠MON=20°.情况1:当∠BDC=2∠BFC时,如图①.∵ AB⊥OM,∠MON=40°,∴ ∠BFC=50°,∴ ∠BDC=2∠BFC=100°.∵ ∠ABO=∠BFC+∠BON=50°+20°=70°,∴ ∠BAC=∠BDC-∠ABO=100°-70°=30°,此时α=30°.情况2:当点C在F的左边,∠DBF=2∠DCF时,如图②.∵ AB⊥OM,∠AOB=20°,∠MON=40°,∴ ∠DBF=∠AOB+∠OAB=20°+90°=110°,∠BFC=50°,∴ ∠DCF=∠DBF=55°,∴ ∠BAC=180°-∠BFC-∠ACF=180°-50°-55°=75°,此时α=75°.情况3:当点C在点F的右边,∠DBF=2∠DCF时,如图③.∵ AB⊥OM,∠AOB=20°,∠MON=40°,∴ ∠DBF=∠ABO=90°-∠AOB=90°-20°=70°,∠AFO=50°,∴ ∠DCF=∠DBF=35°,∠AFC=130°,∴ ∠BAC=180°-∠DCF-∠AFC=180°-35°-130°=15°,此时α=15°.综上所述,当四边形DCFB为“完美四边形”时,α=30°或75°或15°
时间:60分钟
一、 选择题(每小题3分,共24分)
1. 下列语句中,不属于命题的是 ( )
A. 延长线段AB到点C B. 自然数都是整数
C. 有两条边相等的三角形是等腰三角形 D. 平行于同一条直线的两条直线平行
2. 如图,∠A的两条边被一条直线所截,用含α和β的式子表示∠A为 ( )
A. α-β B. β-α
C. 180°-α+β D. 180°-α-β
3. 如图,∠ACB=90°,CD⊥AB,垂足为D,则下列结论错误的是 ( )
A. 图中有三个直角三角形 B. ∠1=∠2
C. ∠1和∠B都是∠A的余角 D. ∠2=∠A
4. 下列命题中,属于真命题的是 ( )
A. 锐角小于它的余角 B. 锐角小于它的补角
C. 锐角与锐角的和是钝角 D. 锐角与钝角的和等于平角
5. 游戏中有数学智慧,找起点游戏规定:从起点走五段相等直路之后回到起点,要求每走完一段直路后向右边偏行.成功的招数不止一招,可助我们成功的一招是 ( )
A. 每走完一段直路后沿向右偏72°方向行走 B. 每段直路要短
C. 每走完一段直路后沿向右偏108°方向行走 D. 每段直路要长
6. 能说明“锐角α、锐角β的和是锐角”是假命题的例证图是 ( )
7. 在如图所示的“箭头”图形中,AB∥CD,∠ABE=∠CDF=80°,∠E=∠F=47°,则∠G的度数是 ( )
A. 80° B. 76° C. 66° D. 56°
8. 如图,∠ABC=∠ACB,AD,BD,CD分别平分△ABC的外角∠EAC、内角∠ABC、外角∠ACF.有下列结论:① AD∥BC;② ∠ACB=2∠ADB;③ ∠ADC=90°-∠ABD;④ ∠BDC=∠BAC.其中,正确的有( )
A. 1个 B. 2个 C. 3个 D. 4个
二、 填空题(每小题2分,共20分)
9. 对一个概念 的语句叫作这个概念的定义.
10. 命题“两直线平行,同位角相等”的逆命题是 .
11. 如图,点D,E分别在线段BC,AC上,连接AD,BE.若∠A=35°,∠B=25°,∠C=50°,则∠1的度数为 .
12. 如图,点D,E分别在△ABC的边AB,AC上,且DE∥BC,点F在线段BC的延长线上.若∠ADE=28°,∠ACF=118°,则∠A的度数为 .
13. 正十二边形的每一个外角等于 °.
14. 如果一个多边形的内角和是外角和的5倍,那么这个多边形是 边形.
15. 将两张三角形纸片按如图所示的方式摆放,量得∠1+∠2+∠3+∠4=220°,则∠5的度数为 .
16. 如图,AB∥CD,DE⊥EF,FG⊥EF,∠ABG=150°,∠CDE=140°,则∠BGF的度数为 .
17. 若一个正方形被截掉一个角后,得到一个多边形,则这个多边形的内角和是 .
18. 如图①,在长方形ABCD中,点E在边AD上,且∠ABE=30°.如图②,分别以BE,CE为折痕进行折叠并压平,∠AED=n°,则∠BCE的度数为 (用含n的代数式表示).
三、 解答题(共56分)
19. (6分)已知命题“如果a>1,那么a2>1”.
(1) 写出这个命题的逆命题;
(2) 举反例说明(1)中得到的逆命题是假命题.
20. (10分)如图,在△ABC中,AC⊥BC,DG⊥BC于点G,EF⊥AB于点E,∠1=∠2.求证:CD⊥AB.
第20题
证明:∵ DG⊥BC,AC⊥BC(已知),
∴ ∠DGB=∠ACB=90°(垂直的定义),
∴ DG∥AC( ),
∴ ∠2= ( ).
∵ ∠1=∠2(已知),
∴ ∠1= (等量代换),
∴ EF∥CD( ),
∴ ∠AEF= ( ).
∵ EF⊥AB(已知),
∴ ∠AEF=90°( ),
∴ ∠ADC=90°( ),
∴ CD⊥AB( ).
21. (10分)如图,在△ABC中,AD⊥BC于点D,BF平分∠ABC交AC于点F,交AD于点E.若∠AEF=∠AFB,试猜想△ABC的形状,并证明你的结论.
第21题
22. (10分)如图,如果直线AB,CD被直线EF所截,EF分别交AB,CD于点O,O',AB∥CD.请用反证法求证:∠EOB=∠EO'D.
第22题
23. (10分)研究一个问题:多边形的一个外角与它不相邻的内角之和具有怎样的数量关系
【探究1】 如图①,请直接写出∠ACD与∠A,∠B之间的数量关系: .
【探究2】 如图②,∠DCE是四边形ABCD的一个外角.求证:∠DCE=∠A+∠B+∠D-180°.
【结论】 若n边形的某一个外角的度数为x°,与这个外角不相邻的内角之和为y°,则x,y与n之间的数量关系为 .
24. (10分)已知∠MON=40°,OE平分∠MON,A,B,C分别是射线OM,OE,ON上的动点(点A,B,C不与点O重合),连接AB,AC,AC交射线OE于点D,设∠BAC=α.
(1) 如图①,若AB∥ON.
① ∠ABO的度数是 .
② 当∠BAD=∠ABD时,∠OAC的度数是 ;当∠BAD=∠BDA时,∠OAC的度数是 .
(2) 在一个四边形中,若存在一个内角是它的对角的2倍,我们称这样的四边形为“完美四边形”.如图②,若AB⊥OM,延长AB交射线ON于点F,当四边形DCFB为“完美四边形”时,求α.
第12章素能测评
一、 1. A 2. B 3. B 4. B 5. A 6. C
7. C 解析:延长AB交EG于点M,延长CD交FG于点N,过点G向左作GK∥AB,得∠KGM=∠EMB.结合AB∥CD,得GK∥CD,从而∠KGN=∠DNF,∴ ∠EGF=∠EMB+∠DNF.由三角形内角和定理的推论可求得∠EMB=33°,∠DNF=33°,∴ ∠EGF=∠EMB+∠DNF=33°+33°=66°.
8. C 解析:① 由AD平分△ABC的外角∠EAC,得∠EAD=∠DAC.由三角形内角和定理的推论,得∠EAC=∠ACB+∠ABC.结合∠ABC=∠ACB,得∠EAD=∠ABC.利用“同位角相等,两直线平行”得AD∥BC.故①正确.② 由AD∥BC,得∠ADB=∠DBC.由BD平分∠ABC,得∠ABD=∠DBC.∴ ∠ABC=2∠ADB,∴ ∠ACB=2∠ADB.故②正确.③ 在△ADC中,∠ADC+∠CAD+∠ACD=180°,利用角的关系,易得∠ADC+∠CAD+∠ACD=∠ADC+2∠ABD+∠ADC=2∠ADC+2∠ABD=180°,∴ ∠ADC=90°-∠ABD.故③正确.④ 由∠BAC+∠ABC=∠ACF,得∠BAC+∠ABC=∠ACF.结合∠BDC+∠DBC=∠ACF,得∠BAC=∠BDC.故④错误.
二、 9. 作出明确规定 10. 同位角相等,两直线平行 11. 70° 12. 90° 13. 30 14. 十二 15. 40° 16. 70° 17. 180°或360°或540° 18. °
三、 19. (1) 如果a2>1,那么a>1 (2) 举反例不唯一,如当a=-2时,a2=4>1,但a<1,故逆命题是假命题
20. 同位角相等,两直线平行 ∠ACD 两直线平行,内错角相等 ∠ACD 同位角相等,两直线平行 ∠ADC 两直线平行,同位角相等 垂直的定义 等量代换 垂直的定义
21. △ABC为直角三角形 ∵ BF平分∠ABC,∴ ∠ABF=∠EBD.∵ AD⊥BC,∴ 在△BDE中,∠EBD+∠BED=90°.∵ ∠AEF=∠BED,∴ ∠ABF+∠AEF=90°.∵ ∠AEF=∠AFB,∴ ∠ABF+∠AFB=90°,∴ ∠BAF=90°,∴ △ABC为直角三角形
22. 假设∠EOB≠∠EO'D.如图,过点O作直线A'B',使∠EOB'=∠EO'D.∴ A'B'∥CD.∵ AB∥CD,∴ 过点O有两条直线AB,A'B'都平行于直线CD.这与基本事实“过直线外一点有且只有一条直线与这条直线平行”矛盾.∴ 假设∠EOB≠∠EO'D不成立,∴ ∠EOB=∠EO'D
23. 【探究1】 ∠ACD=∠A+∠B 【探究2】 ∵ ∠A+∠B+∠D+∠BCD=360°,∠DCE+∠BCD=180°,∴ ∠BCD=360°-(∠A+∠B+∠D),∠BCD=180°-∠DCE,∴ 360°-(∠A+∠B+∠D)=180°-∠DCE,即∠DCE=∠A+∠B+∠D-180°
【结论】 y-x=180(n-3) 解析:∵ n边形的某一个外角的度数是x°,∴ 与这个外角相邻的内角的度数是(180-x)°.∵ 与这个外角不相邻的所有内角之和是y°,∴ (180-x)+y=(n-2)·180,整理,得y-x=180(n-3).
24. (1) ① 20° ② 120° 60° (2) ∵ OE平分∠MON,∠MON=40°,∴ ∠MOE=∠NOE=∠MON=20°.情况1:当∠BDC=2∠BFC时,如图①.∵ AB⊥OM,∠MON=40°,∴ ∠BFC=50°,∴ ∠BDC=2∠BFC=100°.∵ ∠ABO=∠BFC+∠BON=50°+20°=70°,∴ ∠BAC=∠BDC-∠ABO=100°-70°=30°,此时α=30°.情况2:当点C在F的左边,∠DBF=2∠DCF时,如图②.∵ AB⊥OM,∠AOB=20°,∠MON=40°,∴ ∠DBF=∠AOB+∠OAB=20°+90°=110°,∠BFC=50°,∴ ∠DCF=∠DBF=55°,∴ ∠BAC=180°-∠BFC-∠ACF=180°-50°-55°=75°,此时α=75°.情况3:当点C在点F的右边,∠DBF=2∠DCF时,如图③.∵ AB⊥OM,∠AOB=20°,∠MON=40°,∴ ∠DBF=∠ABO=90°-∠AOB=90°-20°=70°,∠AFO=50°,∴ ∠DCF=∠DBF=35°,∠AFC=130°,∴ ∠BAC=180°-∠DCF-∠AFC=180°-35°-130°=15°,此时α=15°.综上所述,当四边形DCFB为“完美四边形”时,α=30°或75°或15°
同课章节目录
- 第7章 平面图形的认识(二)
- 7.1 探索直线平行的条件
- 7.2 探索平行线的性质
- 7.3 图形的平移
- 7.4 认识三角形
- 7.5 多边形的内角和与外角和
- 第8章 幂的运算
- 8.1 同底数幂的乘法
- 8.2 幂的乘方与积的乘方
- 8.3 同底数幂的除法
- 第9章 整式乘法与因式分解
- 9.1 单项式乘单项式
- 9.2 单项式乘多项式
- 9.3 多项式乘多项式
- 9.4 乘法公式
- 9.5 多项式的因式分解
- 第10章 二元一次方程组
- 10.1 二元一次方程
- 10.2 二元一次方程组
- 10.3 解二元一次方程组
- 10.4 三元一次方程组
- 10.5 用二元一次方程解决问题
- 第11章 一元一次不等式
- 11.1 生活中的不等式
- 11.2 不等式的解集
- 11.3 不等式的性质
- 11.4 解一元一次不等式
- 11.5 用一元一次不等式解决问题
- 11.6 一元一次不等式组
- 第12章 证明
- 12.1 定义与命题
- 12.2 证明
- 12.3 互逆命题
