期中素能测评(含答案) 2024-2025学年数学苏科版七年级下册
文档属性
| 名称 | 期中素能测评(含答案) 2024-2025学年数学苏科版七年级下册 |
|
|
| 格式 | docx | ||
| 文件大小 | 497.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-03-29 00:00:00 | ||
图片预览



文档简介
期中素能测评满分:130分
时间:120分钟
一、 选择题(每小题3分,共24分)
1. 下列计算正确的是 ( )
A. a·a3=a4 B. a2+a3=a5
C. a6÷a=a6 D. (a3)4=a7
2. 下列运算正确的是 ( )
A. a(4a+1)=4a2+1 B. (x-2)2=x2+4
C. -60=-1 D. =
3. 下列计算正确的是 ( )
A. (-3x)2=-9x2 B. 7x+5x=12x2
C. (x-3)2=x2-6x+9 D. (x-2y)(x+2y)=x2+4y2
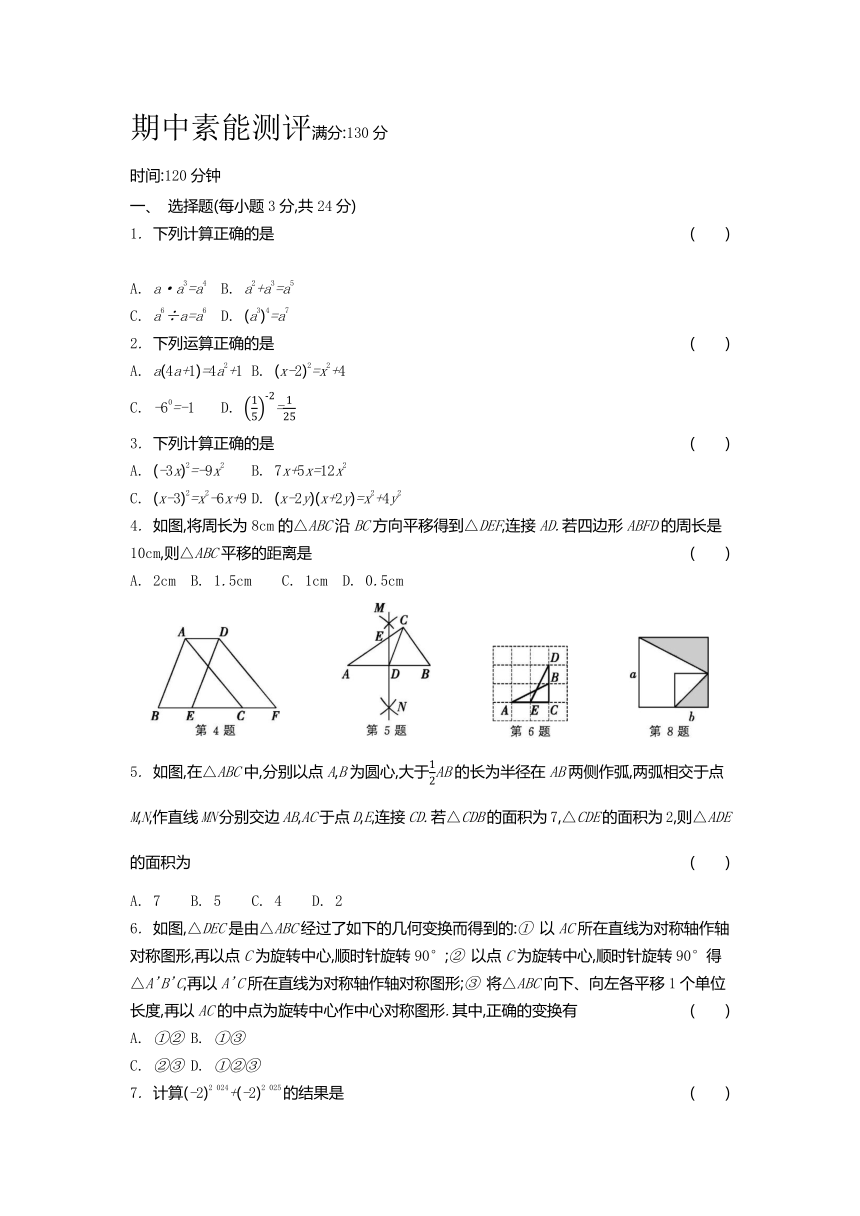
4. 如图,将周长为8cm的△ABC沿BC方向平移得到△DEF,连接AD.若四边形ABFD的周长是10cm,则△ABC平移的距离是 ( )
A. 2cm B. 1.5cm C. 1cm D. 0.5cm
5. 如图,在△ABC中,分别以点A,B为圆心,大于AB的长为半径在AB两侧作弧,两弧相交于点M,N,作直线MN分别交边AB,AC于点D,E,连接CD.若△CDB的面积为7,△CDE的面积为2,则△ADE的面积为 ( )
A. 7 B. 5 C. 4 D. 2
6. 如图,△DEC是由△ABC经过了如下的几何变换而得到的:① 以AC所在直线为对称轴作轴对称图形,再以点C为旋转中心,顺时针旋转90°;② 以点C为旋转中心,顺时针旋转90°得△A'B'C,再以A'C所在直线为对称轴作轴对称图形;③ 将△ABC向下、向左各平移1个单位长度,再以AC的中点为旋转中心作中心对称图形.其中,正确的变换有 ( )
A. ①② B. ①③
C. ②③ D. ①②③
7. 计算(-2)2 024+(-2)2 025的结果是 ( )
A. -2 B. 2
C. 22 024 D. -22 024
8. 如图,两个正方形的边长分别为a和b.若a+b=10,ab=22,则涂色部分的面积是 ( )
A. 15 B. 17 C. 20 D. 22
二、 填空题(每小题3分,共24分)
9. 已知1 nm=0.000 000 001m,则0.5nm用科学记数法表示为 m.
10. 如图,△ABC和△AB'C'关于直线l对称,l交CC'于点D.若AB=4,B'C'=2,CD=0.5,则五边形ABCC'B'的周长为 .
11. 若2m×3n=(4×27)7,则m-n的值为 .
12. 设a=-0.52,b=-5-2,c=,d=,用“<”连接a,b,c,d,得 .
13. 数学课上,老师讲了单项式乘多项式.放学回到家,小明拿出课堂笔记复习,发现一道题:-3xy(7y-5x+1)=-21xy2+15x2y■,■的地方被污染了,你认为■内应填写 .
14. 化简(x+4)(x-4)+(x-3)2的结果为 .
15. 如图,△ABC的边BC的长为4cm.将△ABC平移2cm得到△A'B'C',且BB'⊥BC,则涂色部分的面积为 cm2.
16. 如图,△ABC绕格点O顺时针旋转,旋转的角度为α(0°<α<360°),使旋转后所得三角形的顶点也在格点上,则旋转前后的图形成轴对称时,符合条件的α的度数为 .
三、 解答题(共82分)
17. (6分)计算:
(1) (x+2)(x-3); (2) (2x-7y)2.
18. (12分)计算:
(1) (-a5)÷(-a)3·(-a); (2) (x+y)(x2-xy+y2);
(3) (2a+b)(b-2a)-(a-3b)2; (4) -5x(-x2+2x+1)-(2x+3)(5-x2).
19. (6分)先化简,再求值:(2a+b)(2a-b)-(a+b)(4a-b),其中a=-1.4,b=2.
20. (6分)在网格中,每个小正方形的边长均为1个单位长度,△ABC的三个顶点的位置如图所示,现将△ABC平移,使点A到点A'的位置,B',C'分别是点B,C的对应点.
(1) 请画出平移后的△A'B'C',则△A'B'C'的面积为 ;
(2) 若连接AA',CC',则这两条线段之间的关系是 ;
(3) 在网格中,找一个格点P,能使S△PAC=2S△ABC.
21. (6分)如图,△ACB中,∠ACB=90°,利用直尺与圆规作图(不写作法,保留作图痕迹).
(1) 作∠CAB的平分线,交BC于点D;
(2) 过点D作AB的垂线,垂足为H.
22. (6分)在由相同小正方形组成的网格图中,每个小正方形的顶点称为格点.
(1) △ABC的三个顶点都在格点上.
① 在图①中,画出一个与△ABC成中心对称的格点三角形;
② 在图②中,画出△ABC绕点C逆时针旋转90°后的三角形.
(2) 如图③所示为由5个边长为1的小正方形拼成的图形,请用无刻度的直尺画经过点P的一条直线,使它平分该图形的面积,保留连线的痕迹,不要求说明理由.
23. (6分)现各有甲、乙、丙三种长方形卡片若干张,卡片的边长如图①所示(a>1).某同学分别用6张卡片拼出了两个长方形(不重叠无缝隙),如图②③,其面积分别为S1,S2.
(1) 请用含a的式子分别表示S1,S2,当a=2时,求S1+S2的值;
(2) 比较S1与S2的大小,并说明理由.
24. (6分)已知2a=3,2b=5,2c=75.
(1) 求22a与2c-b+a的值;
(2) 试说明:a+2b=c.
25. (8分)如图,四边形ABCD是正方形,点E在边DC上,将△ADE经顺时针旋转后与△ABF重合,再将△ABF向右平移后与△DCH重合.
(1) 旋转中心为 ,旋转的角度为 °.
(2) 如果连接EF,那么△AEF是怎样的三角形 请说明理由.
(3) 试猜想线段AE和DH之间的数量关系和位置关系,并说明理由.
第25题
26. (10分)如图①,现有A,B,C三种不同的卡片若干张,其中A型卡片是边长为a的正方形,B型卡片是边长为b(b(1) 用上述三种卡片拼出图②,通过两种方法计算图②的面积,可以得到一个代数恒等式,请写出这个代数恒等式: .
(2) 将2张C型卡片沿如图③所示的虚线剪开后,拼成如图④所示的大正方形,请用含a,b的代数式表示涂色部分的面积,即S涂色部分= .
(3) 如图⑤,在长为2a+b、宽为a+2b的长方形中挖去A型、B型卡片各2张.若第(2)问中图④的涂色部分的面积为9,而图⑤的涂色部分的面积为17.5,求图⑤的涂色部分的周长.
27. (10分)将一副三角尺(在△ABC中,∠ACB=90°,∠BAC=30°,在△ADE中,∠ADE=90°,∠CAD=45°,AC=AE)按如图①所示的方式放置.如图②,将△ADE绕点A按逆时针方向以每秒5°的速度旋转,设旋转的时间为t秒(0≤t≤36).
(1) 图①中,∠BAD= °;
(2) 在△ADE绕点A旋转的过程中,当DE与△ABC的一边平行时,求t的值;
(3) 在△ADE绕点A旋转的过程中,探究∠CAE与∠BAD之间的数量关系.
期中素能测评
一、 1. A 2. C 3. C 4. C 5. B 6. A 7. D
8. B 解析:由题意,得涂色部分的面积为(a-b)·a+b2=(a2+b2)-ab.因为a+b=10,ab=22,所以a2+b2=(a+b)2-2ab=102-2×22=56,所以涂色部分的面积是×56-×22=28-11=17.
二、 9. 5×10-10 10. 13 11. -7 12. a16. 90°或180°或270° 解析:如图,符合条件的α的度数为90°或180°或270°.
三、 17. (1) x2-x-6 (2) 4x2-28xy+49y2
18. (1) -a3 (2) x3+y3 (3) -5a2+6ab-8b2 (4) 7x3-7x2-15x-15
19. 原式=4a2-b2-(4a2-ab+4ab-b2)=4a2-b2-4a2+ab-4ab+b2=-3ab.当a=-1.4,b=2时,原式=-3×(-1.4)×2=8.4
20. (1) 如图,△A'B'C'即为所求 3.5 (2) 平行且相等 (3) 如图,点P即为所求(答案不唯一)
21. (1) 如图,射线AD即为所求 (2) 如图,直线DH即为所求
22. (1) ① 答案不唯一,如图①,△A1B1C即为所求 ② 如图②,△A2B2C即为所求 (2) 如图③,直线l即为所求
23. (1) 根据题意,得S1=(a+2)(a+1)=a2+3a+2,S2=(5a+1)×1=5a+1.当a=2时,S1+S2=4+6+2+10+1=23 (2) S1>S2 理由:S1-S2=a2+3a+2-5a-1=a2-2a+1=(a-1)2.因为a>1,所以(a-1)2>0,所以S1-S2>0,所以S1>S2.
24. (1) 22a=(2a)2=32=9,2c-b+a=2c÷2b×2a=75÷5×3=45 (2) 因为22b=52=25,所以2a+2b=2a×22b=3×25=75.因为2c=75,所以2a+2b=2c,即a+2b=c
25. (1) 点A 90 (2) △AEF是等腰直角三角形 理由:连接EF.根据题意,得△ADE绕点A顺时针旋转90°后与△ABF重合,所以AF=AE,∠FAE=∠BAD=90°,所以△AEF是等腰直角三角形. (3) AE=DH,AE⊥DH 理由:因为△ABF向右平移后与△DCH重合,所以AF=DH,AF∥DH,所以∠FAE=∠HGE.由(2),得∠FAE=90°,AF=AE,所以∠HGE=90°,AE=DH,所以AE⊥DH.
26. (1) (a+b)2=a2+2ab+b2 (2) (a+b)2-2ab(或a2+b2) (3) 由题图⑤,可知(2a+b)(a+2b)-2a2-2b2=17.5,化简,得ab=3.5.由题图④,可知(a+b)2-2ab=9.把ab=3.5代入,得(a+b)2=16.因为a+b>0,所以a+b=4.所以题图⑤的涂色部分的周长为2(2a+b)+2(a+2b)+2(2a+2b)=10(a+b)=10×4=40
27. (1) 15 (2) 根据题意,得∠CAE=(5t)°(0≤t≤36).如图①,当DE∥AC时,∠DEA=∠CAE=45°=(5t)°,解得t=9.如图②,当DE∥AB时,∠DEA=∠BAE=45°,所以∠CAE=∠BAE+∠BAC=75°=(5t)°,解得t=15.如图③,当DE∥BC时,易得D,A,C三点在同一条直线上,所以∠CAE=180°-∠DAE=135°=(5t)°,解得t=27.综上所述,当DE与△ABC的一边平行时,t的值为9或15或27 (3) 当点E在AB边上时,由(5t)°=30°,得t=6;当点D在BA的延长线上时,由(5t)°=180°-45°+30°,得t=33.分3种情况讨论:当0≤t≤6时,如图④,因为∠BAD=∠DAE-∠BAE=45°-(∠BAC-∠CAE),所以∠BAD=15°+∠CAE.当6
时间:120分钟
一、 选择题(每小题3分,共24分)
1. 下列计算正确的是 ( )
A. a·a3=a4 B. a2+a3=a5
C. a6÷a=a6 D. (a3)4=a7
2. 下列运算正确的是 ( )
A. a(4a+1)=4a2+1 B. (x-2)2=x2+4
C. -60=-1 D. =
3. 下列计算正确的是 ( )
A. (-3x)2=-9x2 B. 7x+5x=12x2
C. (x-3)2=x2-6x+9 D. (x-2y)(x+2y)=x2+4y2
4. 如图,将周长为8cm的△ABC沿BC方向平移得到△DEF,连接AD.若四边形ABFD的周长是10cm,则△ABC平移的距离是 ( )
A. 2cm B. 1.5cm C. 1cm D. 0.5cm
5. 如图,在△ABC中,分别以点A,B为圆心,大于AB的长为半径在AB两侧作弧,两弧相交于点M,N,作直线MN分别交边AB,AC于点D,E,连接CD.若△CDB的面积为7,△CDE的面积为2,则△ADE的面积为 ( )
A. 7 B. 5 C. 4 D. 2
6. 如图,△DEC是由△ABC经过了如下的几何变换而得到的:① 以AC所在直线为对称轴作轴对称图形,再以点C为旋转中心,顺时针旋转90°;② 以点C为旋转中心,顺时针旋转90°得△A'B'C,再以A'C所在直线为对称轴作轴对称图形;③ 将△ABC向下、向左各平移1个单位长度,再以AC的中点为旋转中心作中心对称图形.其中,正确的变换有 ( )
A. ①② B. ①③
C. ②③ D. ①②③
7. 计算(-2)2 024+(-2)2 025的结果是 ( )
A. -2 B. 2
C. 22 024 D. -22 024
8. 如图,两个正方形的边长分别为a和b.若a+b=10,ab=22,则涂色部分的面积是 ( )
A. 15 B. 17 C. 20 D. 22
二、 填空题(每小题3分,共24分)
9. 已知1 nm=0.000 000 001m,则0.5nm用科学记数法表示为 m.
10. 如图,△ABC和△AB'C'关于直线l对称,l交CC'于点D.若AB=4,B'C'=2,CD=0.5,则五边形ABCC'B'的周长为 .
11. 若2m×3n=(4×27)7,则m-n的值为 .
12. 设a=-0.52,b=-5-2,c=,d=,用“<”连接a,b,c,d,得 .
13. 数学课上,老师讲了单项式乘多项式.放学回到家,小明拿出课堂笔记复习,发现一道题:-3xy(7y-5x+1)=-21xy2+15x2y■,■的地方被污染了,你认为■内应填写 .
14. 化简(x+4)(x-4)+(x-3)2的结果为 .
15. 如图,△ABC的边BC的长为4cm.将△ABC平移2cm得到△A'B'C',且BB'⊥BC,则涂色部分的面积为 cm2.
16. 如图,△ABC绕格点O顺时针旋转,旋转的角度为α(0°<α<360°),使旋转后所得三角形的顶点也在格点上,则旋转前后的图形成轴对称时,符合条件的α的度数为 .
三、 解答题(共82分)
17. (6分)计算:
(1) (x+2)(x-3); (2) (2x-7y)2.
18. (12分)计算:
(1) (-a5)÷(-a)3·(-a); (2) (x+y)(x2-xy+y2);
(3) (2a+b)(b-2a)-(a-3b)2; (4) -5x(-x2+2x+1)-(2x+3)(5-x2).
19. (6分)先化简,再求值:(2a+b)(2a-b)-(a+b)(4a-b),其中a=-1.4,b=2.
20. (6分)在网格中,每个小正方形的边长均为1个单位长度,△ABC的三个顶点的位置如图所示,现将△ABC平移,使点A到点A'的位置,B',C'分别是点B,C的对应点.
(1) 请画出平移后的△A'B'C',则△A'B'C'的面积为 ;
(2) 若连接AA',CC',则这两条线段之间的关系是 ;
(3) 在网格中,找一个格点P,能使S△PAC=2S△ABC.
21. (6分)如图,△ACB中,∠ACB=90°,利用直尺与圆规作图(不写作法,保留作图痕迹).
(1) 作∠CAB的平分线,交BC于点D;
(2) 过点D作AB的垂线,垂足为H.
22. (6分)在由相同小正方形组成的网格图中,每个小正方形的顶点称为格点.
(1) △ABC的三个顶点都在格点上.
① 在图①中,画出一个与△ABC成中心对称的格点三角形;
② 在图②中,画出△ABC绕点C逆时针旋转90°后的三角形.
(2) 如图③所示为由5个边长为1的小正方形拼成的图形,请用无刻度的直尺画经过点P的一条直线,使它平分该图形的面积,保留连线的痕迹,不要求说明理由.
23. (6分)现各有甲、乙、丙三种长方形卡片若干张,卡片的边长如图①所示(a>1).某同学分别用6张卡片拼出了两个长方形(不重叠无缝隙),如图②③,其面积分别为S1,S2.
(1) 请用含a的式子分别表示S1,S2,当a=2时,求S1+S2的值;
(2) 比较S1与S2的大小,并说明理由.
24. (6分)已知2a=3,2b=5,2c=75.
(1) 求22a与2c-b+a的值;
(2) 试说明:a+2b=c.
25. (8分)如图,四边形ABCD是正方形,点E在边DC上,将△ADE经顺时针旋转后与△ABF重合,再将△ABF向右平移后与△DCH重合.
(1) 旋转中心为 ,旋转的角度为 °.
(2) 如果连接EF,那么△AEF是怎样的三角形 请说明理由.
(3) 试猜想线段AE和DH之间的数量关系和位置关系,并说明理由.
第25题
26. (10分)如图①,现有A,B,C三种不同的卡片若干张,其中A型卡片是边长为a的正方形,B型卡片是边长为b(b
(2) 将2张C型卡片沿如图③所示的虚线剪开后,拼成如图④所示的大正方形,请用含a,b的代数式表示涂色部分的面积,即S涂色部分= .
(3) 如图⑤,在长为2a+b、宽为a+2b的长方形中挖去A型、B型卡片各2张.若第(2)问中图④的涂色部分的面积为9,而图⑤的涂色部分的面积为17.5,求图⑤的涂色部分的周长.
27. (10分)将一副三角尺(在△ABC中,∠ACB=90°,∠BAC=30°,在△ADE中,∠ADE=90°,∠CAD=45°,AC=AE)按如图①所示的方式放置.如图②,将△ADE绕点A按逆时针方向以每秒5°的速度旋转,设旋转的时间为t秒(0≤t≤36).
(1) 图①中,∠BAD= °;
(2) 在△ADE绕点A旋转的过程中,当DE与△ABC的一边平行时,求t的值;
(3) 在△ADE绕点A旋转的过程中,探究∠CAE与∠BAD之间的数量关系.
期中素能测评
一、 1. A 2. C 3. C 4. C 5. B 6. A 7. D
8. B 解析:由题意,得涂色部分的面积为(a-b)·a+b2=(a2+b2)-ab.因为a+b=10,ab=22,所以a2+b2=(a+b)2-2ab=102-2×22=56,所以涂色部分的面积是×56-×22=28-11=17.
二、 9. 5×10-10 10. 13 11. -7 12. a
三、 17. (1) x2-x-6 (2) 4x2-28xy+49y2
18. (1) -a3 (2) x3+y3 (3) -5a2+6ab-8b2 (4) 7x3-7x2-15x-15
19. 原式=4a2-b2-(4a2-ab+4ab-b2)=4a2-b2-4a2+ab-4ab+b2=-3ab.当a=-1.4,b=2时,原式=-3×(-1.4)×2=8.4
20. (1) 如图,△A'B'C'即为所求 3.5 (2) 平行且相等 (3) 如图,点P即为所求(答案不唯一)
21. (1) 如图,射线AD即为所求 (2) 如图,直线DH即为所求
22. (1) ① 答案不唯一,如图①,△A1B1C即为所求 ② 如图②,△A2B2C即为所求 (2) 如图③,直线l即为所求
23. (1) 根据题意,得S1=(a+2)(a+1)=a2+3a+2,S2=(5a+1)×1=5a+1.当a=2时,S1+S2=4+6+2+10+1=23 (2) S1>S2 理由:S1-S2=a2+3a+2-5a-1=a2-2a+1=(a-1)2.因为a>1,所以(a-1)2>0,所以S1-S2>0,所以S1>S2.
24. (1) 22a=(2a)2=32=9,2c-b+a=2c÷2b×2a=75÷5×3=45 (2) 因为22b=52=25,所以2a+2b=2a×22b=3×25=75.因为2c=75,所以2a+2b=2c,即a+2b=c
25. (1) 点A 90 (2) △AEF是等腰直角三角形 理由:连接EF.根据题意,得△ADE绕点A顺时针旋转90°后与△ABF重合,所以AF=AE,∠FAE=∠BAD=90°,所以△AEF是等腰直角三角形. (3) AE=DH,AE⊥DH 理由:因为△ABF向右平移后与△DCH重合,所以AF=DH,AF∥DH,所以∠FAE=∠HGE.由(2),得∠FAE=90°,AF=AE,所以∠HGE=90°,AE=DH,所以AE⊥DH.
26. (1) (a+b)2=a2+2ab+b2 (2) (a+b)2-2ab(或a2+b2) (3) 由题图⑤,可知(2a+b)(a+2b)-2a2-2b2=17.5,化简,得ab=3.5.由题图④,可知(a+b)2-2ab=9.把ab=3.5代入,得(a+b)2=16.因为a+b>0,所以a+b=4.所以题图⑤的涂色部分的周长为2(2a+b)+2(a+2b)+2(2a+2b)=10(a+b)=10×4=40
27. (1) 15 (2) 根据题意,得∠CAE=(5t)°(0≤t≤36).如图①,当DE∥AC时,∠DEA=∠CAE=45°=(5t)°,解得t=9.如图②,当DE∥AB时,∠DEA=∠BAE=45°,所以∠CAE=∠BAE+∠BAC=75°=(5t)°,解得t=15.如图③,当DE∥BC时,易得D,A,C三点在同一条直线上,所以∠CAE=180°-∠DAE=135°=(5t)°,解得t=27.综上所述,当DE与△ABC的一边平行时,t的值为9或15或27 (3) 当点E在AB边上时,由(5t)°=30°,得t=6;当点D在BA的延长线上时,由(5t)°=180°-45°+30°,得t=33.分3种情况讨论:当0≤t≤6时,如图④,因为∠BAD=∠DAE-∠BAE=45°-(∠BAC-∠CAE),所以∠BAD=15°+∠CAE.当6
同课章节目录
