浙江省宁波市宋诏桥中学2024-2025学年第二学期九年级数学三月模拟考试(含答案)
文档属性
| 名称 | 浙江省宁波市宋诏桥中学2024-2025学年第二学期九年级数学三月模拟考试(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 338.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-03-30 12:15:04 | ||
图片预览



文档简介
2024学年第二学期九年级数学学科测试
一. 选择题 (每题 3 分, 共 30 分)
1. -2 的绝对值为 ( )
A. 2 B. -2 C. D.
2. 下列图形属于中心对称图形的是( )
A. B. C. D.
3. 下列运算正确的是( )
A. B. C. D.
4. 一个不透明的袋中有 4 个白球, 3 个黄球和 2 个红球, 这些球除颜色外其余都相同, 则从袋中随机摸出一个球是黄球的概率为( )
A. B. C. D.
5. 已知 、 、c都是实数,并且 ,那么下列式子中正确的是( )
A. B. C. D.
6. 某班要从 9 名 400 米跑成绩各不相同的同学中选 4 名参加 米接力赛,而这 9 名同学只知道自己的成绩,要想让他们知道自己是否入选,老师只需公布他们成绩的( )
A. 平均数 B. 众数 C. 中位数 D. 方差
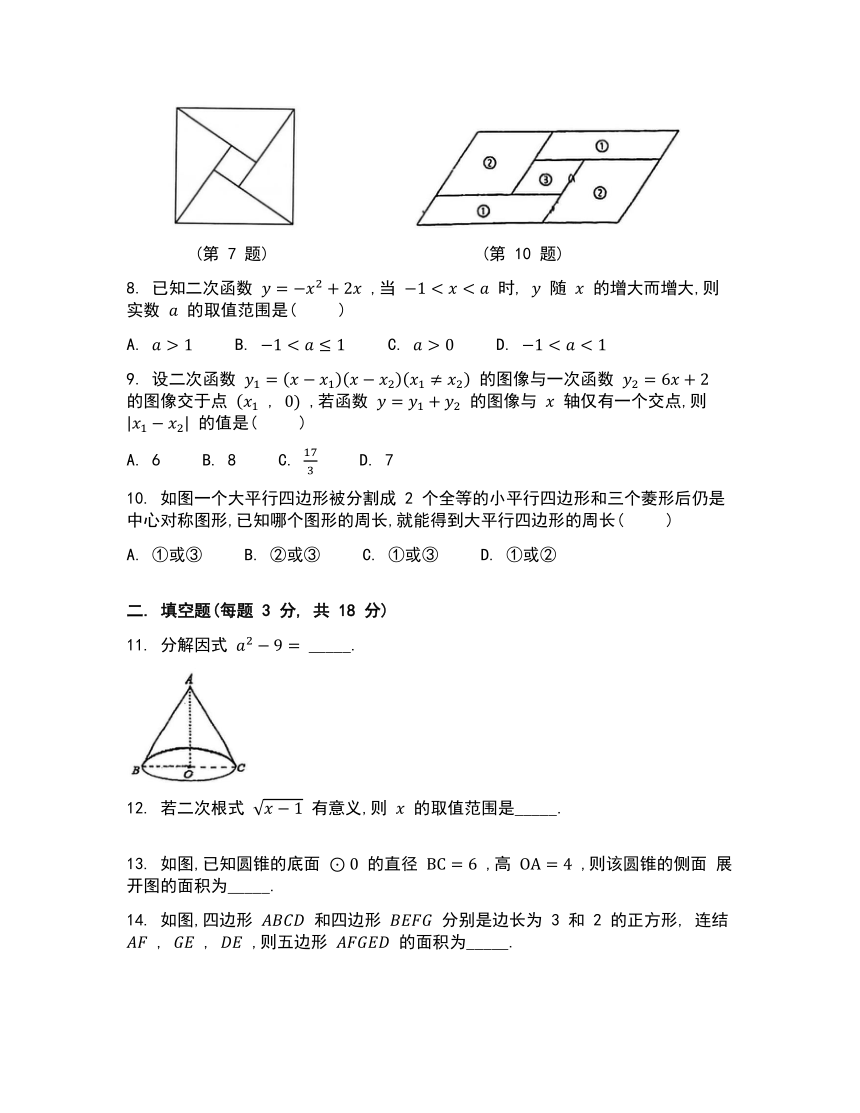
7. 四个全等的直角三角形围成一个大正方形, 中间空出的部分是一个小正方形, 这样就组成了一个 “赵爽弦图” (如图). 如果小正方形面积为 1 , 大正方形面积为 25 , 直角三角形中较小的锐角为 ,那么 的值是 ( )
A. B. C. D.
(第 7 题) (第 10 题)
8. 已知二次函数 ,当 时, 随 的增大而增大,则实数 的取值范围是( )
A. B. C. D.
9. 设二次函数 的图像与一次函数 的图像交于点 , ,若函数 的图像与 轴仅有一个交点,则 的值是( )
A. 6 B. 8 C. D. 7
10. 如图一个大平行四边形被分割成 2 个全等的小平行四边形和三个菱形后仍是中心对称图形,已知哪个图形的周长,就能得到大平行四边形的周长( )
A. ①或③ B. ②或③ C. ①或③ D. ①或②
二. 填空题(每题 3 分, 共 18 分)
11. 分解因式 _____.
12. 若二次根式 有意义,则 的取值范围是_____.
13. 如图,已知圆锥的底面 的直径 ,高 ,则该圆锥的侧面 展开图的面积为_____.
14. 如图,四边形 和四边形 分别是边长为 3 和 2 的正方形, 连结 , , ,则五边形 的面积为_____.
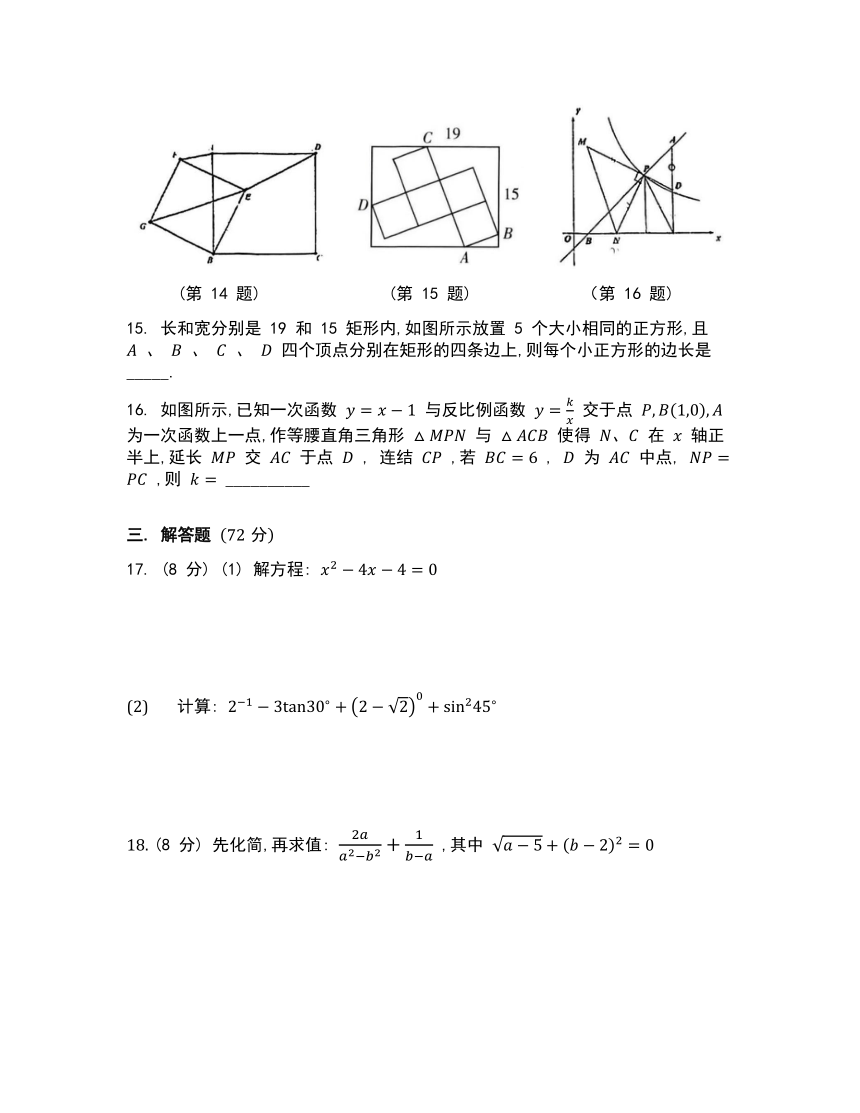
(第 14 题) (第 15 题) (第 16 题)
15. 长和宽分别是 19 和 15 矩形内,如图所示放置 5 个大小相同的正方形,且 、 、 、 四个顶点分别在矩形的四条边上,则每个小正方形的边长是_____.
16. 如图所示,已知一次函数 与反比例函数 交于点 为一次函数上一点,作等腰直角三角形 与 使得 在 轴正半上,延长 交 于点 , 连结 ,若 , 为 中点, ,则 __________
三. 解答题
17. (8 分) (1) 解方程:
计算:
(8 分) 先化简,再求值: ,其中
19. (8 分)为了迎接体育中考,某中学对全校初三男生进行了立定跳远项目测试,并从参加测试的 200 名男生中随机抽取了部分男生的测试成绩(单位:米,精确到 0.01 米)作为样本进行分析, 绘制了如图所示的频数分布直方图(每组含最低值, 不含最高值). 已知图中从左到右每个小长方形的高的比依次为 ,其中 这一小组的频数为 8 ,
请根据有关信息解答下列问题:
(1)填空:这次调查的样本容量为_____,
2.40~2.60 这一小组的频率为_____;
(2)请指出样本成绩的中位数落在哪一小组内;
( 3 )样本中男生立定跳远的人均成绩不低于多少米
请估计该校初三男生立定跳远成绩在 2.00 米以上 (包括 2.00 米) 的约有多少人
20. (8分)如果二次函数 的图像经过点(-1,0),那么称此二次函数为 “定点抛物线”.
(1)试判断二次函数 的图像是否为 “定点抛物线” .
( 2 )若定点抛物线 与 轴只有一个公共点,求 的值.
21. (8分)“超速已成为马路主要安全隐患之一”. 如图,一条公路建成通车,在某笔直路段 MN 限速 100 千米/小时,为了检测车辆是否超速,在公路 MN 旁设立了观测点 ,从观测点 测得一小车从点 行驶到点 用了 5 秒钟,已知 米, 则此车超速了吗 请说明理由. (参考数据: )
22. (10分) 冰糖心苹果是阿克苏的特色农产品,它色泽光亮自然,水分足,果肉脆,口味甜, 深受市民喜爱。上市时, 王经理按市场价格 6 元/千克收购了 2000 千克苹果放入冷库中。 据预测,苹果的市场价格每天每千克将上涨 0.2 元,但冷库存放这批苹果每天需要支出各种费用 160 元,而且苹果在冷库中最多可以保存 50 天,同时,每天有 10 千克的苹果损坏不能出售。
(1)若存放 天后,将这批苹果一次性出售,设这批苹果的销售总金额为 元,试写出 与 之间的函数解析式;
(2)王经理想获得 3850 元的利润,需将这批苹果存放多少天后出售?(利润=销售总金额- 收购成本-各种费用)
(3)王经理将这批苹果存放多少天后出售可获得最大利润?最大利润是多少?
23.(10分)根据以下素材,探索完成任务
设计弹弹珠游戏
素材 1: 某班级组织趣味弹弹珠游戏, 设计如下: (1)距离水平地面 米处有一带弹簧的装置; (2)每次将弹簧向左挤压相同距离,松手后弹珠从 点水平飞出, 研究路径时弹珠直径可忽略, 如图 1. 图 1
素材 2: 某班进行试玩, 发现: 当弹珠从 点飞出后形成的路径是抛物线的一 半, 并正好从挡板 1 的顶部经过, 此时带弹簧的装置 距离水平地面的高度 米,挡板 1 至 点距离为 0.6 米,挡板 1 的高度为 0.4 米,如图 2. 图 2
素材 3: 弹珠游戏装置变化,如图 3: (1)在距离 点 0.8 米处新增长度为 0.2 米的挡板 2, 挡板 1 与挡板 2 之间记为区域 I : (2)在距离 点 1 米处新增长度为 0.1 米的挡板 3 , 挡板 2 与挡板 3 之间记为区域 II. 图 3
问题解决
任务 1: 确定弹珠路径. 请在图 2 中以 点为原点建立直角坐标系,并求出弹珠飞出路径对 应的抛物线解析式.
任务 2: 确定移动方案. 要想让弹珠飞出后落入区域 I 内,该弹簧装置向上移动的距离 要 满足什么条件?
任务 3:灵活变通. 根据同学们的实际游戏情况,上下移动装置很难精准将弹珠落入固定区 域内, 希望作出调整. 现做出如下改动, 在任务 1 的基础上, 先将装置向上移动 0.3 米, 再 通过左右移动三块挡板(区域 I 和区域 II 的宽度不改变),让弹珠落入得分更高的区域 II 内, 请计算挡板 3 横坐标的取值范围。
24. (12分)如图 1,四边形 是 的内接四边形, 为对角线,且 为 的直径, ,已知 , .
(1)求 的长;
(2)如图 2, 为 上一点,过 作 ,其反向延长线交 于点 ,连结 、 、 ,若 ,
① 求 的值;
②试求 的长.
图 1 图 2 (备用图)
2024学年第二学期九年级数学学科测试答案
一.选择题(30分)
1. A 2. C 3.D 4. B 5. B 6. C 7. A 8. B 9. A 10.D
二.填空题(18分)
11.(a+3)(a-3)
12.
13.
14. 4.5
15.
16. 20
三.解答题(72分)
17.(1), (3分)
(2)
(4分)
(5分)
18.解: (2分)
(3分)
(4分)
(6分)
(8分)
19.解:(1)40,0.15 (2分)
(2)2.00~2.20 (4分)
(3)2.03米 (6分)
(4)140人 (8分)
20.(1)∵当x=-1时,y=2+5-7=0,
∴二次函数图像经过点(-1,0),
∴二次函数y=2x2-5x-7是定点抛物线. (3分)
由题意得, (6分)
∴
∴ (8分)
21. 解:此车超速.
理由如下:过C作CH⊥MN,
∵∠CBN=60°,BC=400米,
∴CH=BC sin60°=400×=200(米), (2分)
BH=BC cos60°=200(米), (3分)
∵∠CAN=45°,
∴AH=CH=200米, (4分)
∴AB=200﹣200≈146.4(m), (5分)
∵100千米/小时=m/s,
∴(m)<146.4(m), (7分)
∴此车超速. (8分)
22.(1) (3分)
(2)
(不合题意,舍去)
答:需将这批苹果存放35天后出售。 (6分)
(3)
所以当x=45时,W最大=4050,即存放45天后出售可获得最大利润,最大利润为4050元。 (10分)
23.任务1:() (2分)
任务2:设
把代入得,.
∴ (5分)
任务3:由题意得, (6分)
当时,(负值舍去) (7分)
此时挡板1横坐标,,不会被挡板1挡住.(8分)
当时,(负值舍去) (9分)
∴ (10分)
24.(1)连结OD、OC,设OD与AC交于点P
∵AD=DC,∴,∴AC⊥OD,∴P为AC中点,
又O为圆心,AB为直径∴OP=BC=,
由S△ADC=S△ACB可知DP=BC=1,∴AB=3,从而AC=2 (4分)
(2)①∵GF⊥AC,AG⊥BG,∠ACG=∠ABG
∴∠BAG=∠FGC,又∠CAB=∠CGB=∠AGF,
∴∠CAG=∠CGA,∴CG=AC=2.
设AF=a,由tan∠CAB=tan∠AGF=可知,
FG=2a,AG=3a,∴FC=2-a,
∴(2-a)2+(2a)2=(2)2,
解得a=,从而AG=,∴=. (8分)
②由△AFE∽△ACB,∴,
∴EF=,AE=,∴EG=FG-EF=,EB=
又由①得∠BCH=∠BAG=∠FGC,
∴△BCH∽△EGH,∴,解得BH=. (12分)
一. 选择题 (每题 3 分, 共 30 分)
1. -2 的绝对值为 ( )
A. 2 B. -2 C. D.
2. 下列图形属于中心对称图形的是( )
A. B. C. D.
3. 下列运算正确的是( )
A. B. C. D.
4. 一个不透明的袋中有 4 个白球, 3 个黄球和 2 个红球, 这些球除颜色外其余都相同, 则从袋中随机摸出一个球是黄球的概率为( )
A. B. C. D.
5. 已知 、 、c都是实数,并且 ,那么下列式子中正确的是( )
A. B. C. D.
6. 某班要从 9 名 400 米跑成绩各不相同的同学中选 4 名参加 米接力赛,而这 9 名同学只知道自己的成绩,要想让他们知道自己是否入选,老师只需公布他们成绩的( )
A. 平均数 B. 众数 C. 中位数 D. 方差
7. 四个全等的直角三角形围成一个大正方形, 中间空出的部分是一个小正方形, 这样就组成了一个 “赵爽弦图” (如图). 如果小正方形面积为 1 , 大正方形面积为 25 , 直角三角形中较小的锐角为 ,那么 的值是 ( )
A. B. C. D.
(第 7 题) (第 10 题)
8. 已知二次函数 ,当 时, 随 的增大而增大,则实数 的取值范围是( )
A. B. C. D.
9. 设二次函数 的图像与一次函数 的图像交于点 , ,若函数 的图像与 轴仅有一个交点,则 的值是( )
A. 6 B. 8 C. D. 7
10. 如图一个大平行四边形被分割成 2 个全等的小平行四边形和三个菱形后仍是中心对称图形,已知哪个图形的周长,就能得到大平行四边形的周长( )
A. ①或③ B. ②或③ C. ①或③ D. ①或②
二. 填空题(每题 3 分, 共 18 分)
11. 分解因式 _____.
12. 若二次根式 有意义,则 的取值范围是_____.
13. 如图,已知圆锥的底面 的直径 ,高 ,则该圆锥的侧面 展开图的面积为_____.
14. 如图,四边形 和四边形 分别是边长为 3 和 2 的正方形, 连结 , , ,则五边形 的面积为_____.
(第 14 题) (第 15 题) (第 16 题)
15. 长和宽分别是 19 和 15 矩形内,如图所示放置 5 个大小相同的正方形,且 、 、 、 四个顶点分别在矩形的四条边上,则每个小正方形的边长是_____.
16. 如图所示,已知一次函数 与反比例函数 交于点 为一次函数上一点,作等腰直角三角形 与 使得 在 轴正半上,延长 交 于点 , 连结 ,若 , 为 中点, ,则 __________
三. 解答题
17. (8 分) (1) 解方程:
计算:
(8 分) 先化简,再求值: ,其中
19. (8 分)为了迎接体育中考,某中学对全校初三男生进行了立定跳远项目测试,并从参加测试的 200 名男生中随机抽取了部分男生的测试成绩(单位:米,精确到 0.01 米)作为样本进行分析, 绘制了如图所示的频数分布直方图(每组含最低值, 不含最高值). 已知图中从左到右每个小长方形的高的比依次为 ,其中 这一小组的频数为 8 ,
请根据有关信息解答下列问题:
(1)填空:这次调查的样本容量为_____,
2.40~2.60 这一小组的频率为_____;
(2)请指出样本成绩的中位数落在哪一小组内;
( 3 )样本中男生立定跳远的人均成绩不低于多少米
请估计该校初三男生立定跳远成绩在 2.00 米以上 (包括 2.00 米) 的约有多少人
20. (8分)如果二次函数 的图像经过点(-1,0),那么称此二次函数为 “定点抛物线”.
(1)试判断二次函数 的图像是否为 “定点抛物线” .
( 2 )若定点抛物线 与 轴只有一个公共点,求 的值.
21. (8分)“超速已成为马路主要安全隐患之一”. 如图,一条公路建成通车,在某笔直路段 MN 限速 100 千米/小时,为了检测车辆是否超速,在公路 MN 旁设立了观测点 ,从观测点 测得一小车从点 行驶到点 用了 5 秒钟,已知 米, 则此车超速了吗 请说明理由. (参考数据: )
22. (10分) 冰糖心苹果是阿克苏的特色农产品,它色泽光亮自然,水分足,果肉脆,口味甜, 深受市民喜爱。上市时, 王经理按市场价格 6 元/千克收购了 2000 千克苹果放入冷库中。 据预测,苹果的市场价格每天每千克将上涨 0.2 元,但冷库存放这批苹果每天需要支出各种费用 160 元,而且苹果在冷库中最多可以保存 50 天,同时,每天有 10 千克的苹果损坏不能出售。
(1)若存放 天后,将这批苹果一次性出售,设这批苹果的销售总金额为 元,试写出 与 之间的函数解析式;
(2)王经理想获得 3850 元的利润,需将这批苹果存放多少天后出售?(利润=销售总金额- 收购成本-各种费用)
(3)王经理将这批苹果存放多少天后出售可获得最大利润?最大利润是多少?
23.(10分)根据以下素材,探索完成任务
设计弹弹珠游戏
素材 1: 某班级组织趣味弹弹珠游戏, 设计如下: (1)距离水平地面 米处有一带弹簧的装置; (2)每次将弹簧向左挤压相同距离,松手后弹珠从 点水平飞出, 研究路径时弹珠直径可忽略, 如图 1. 图 1
素材 2: 某班进行试玩, 发现: 当弹珠从 点飞出后形成的路径是抛物线的一 半, 并正好从挡板 1 的顶部经过, 此时带弹簧的装置 距离水平地面的高度 米,挡板 1 至 点距离为 0.6 米,挡板 1 的高度为 0.4 米,如图 2. 图 2
素材 3: 弹珠游戏装置变化,如图 3: (1)在距离 点 0.8 米处新增长度为 0.2 米的挡板 2, 挡板 1 与挡板 2 之间记为区域 I : (2)在距离 点 1 米处新增长度为 0.1 米的挡板 3 , 挡板 2 与挡板 3 之间记为区域 II. 图 3
问题解决
任务 1: 确定弹珠路径. 请在图 2 中以 点为原点建立直角坐标系,并求出弹珠飞出路径对 应的抛物线解析式.
任务 2: 确定移动方案. 要想让弹珠飞出后落入区域 I 内,该弹簧装置向上移动的距离 要 满足什么条件?
任务 3:灵活变通. 根据同学们的实际游戏情况,上下移动装置很难精准将弹珠落入固定区 域内, 希望作出调整. 现做出如下改动, 在任务 1 的基础上, 先将装置向上移动 0.3 米, 再 通过左右移动三块挡板(区域 I 和区域 II 的宽度不改变),让弹珠落入得分更高的区域 II 内, 请计算挡板 3 横坐标的取值范围。
24. (12分)如图 1,四边形 是 的内接四边形, 为对角线,且 为 的直径, ,已知 , .
(1)求 的长;
(2)如图 2, 为 上一点,过 作 ,其反向延长线交 于点 ,连结 、 、 ,若 ,
① 求 的值;
②试求 的长.
图 1 图 2 (备用图)
2024学年第二学期九年级数学学科测试答案
一.选择题(30分)
1. A 2. C 3.D 4. B 5. B 6. C 7. A 8. B 9. A 10.D
二.填空题(18分)
11.(a+3)(a-3)
12.
13.
14. 4.5
15.
16. 20
三.解答题(72分)
17.(1), (3分)
(2)
(4分)
(5分)
18.解: (2分)
(3分)
(4分)
(6分)
(8分)
19.解:(1)40,0.15 (2分)
(2)2.00~2.20 (4分)
(3)2.03米 (6分)
(4)140人 (8分)
20.(1)∵当x=-1时,y=2+5-7=0,
∴二次函数图像经过点(-1,0),
∴二次函数y=2x2-5x-7是定点抛物线. (3分)
由题意得, (6分)
∴
∴ (8分)
21. 解:此车超速.
理由如下:过C作CH⊥MN,
∵∠CBN=60°,BC=400米,
∴CH=BC sin60°=400×=200(米), (2分)
BH=BC cos60°=200(米), (3分)
∵∠CAN=45°,
∴AH=CH=200米, (4分)
∴AB=200﹣200≈146.4(m), (5分)
∵100千米/小时=m/s,
∴(m)<146.4(m), (7分)
∴此车超速. (8分)
22.(1) (3分)
(2)
(不合题意,舍去)
答:需将这批苹果存放35天后出售。 (6分)
(3)
所以当x=45时,W最大=4050,即存放45天后出售可获得最大利润,最大利润为4050元。 (10分)
23.任务1:() (2分)
任务2:设
把代入得,.
∴ (5分)
任务3:由题意得, (6分)
当时,(负值舍去) (7分)
此时挡板1横坐标,,不会被挡板1挡住.(8分)
当时,(负值舍去) (9分)
∴ (10分)
24.(1)连结OD、OC,设OD与AC交于点P
∵AD=DC,∴,∴AC⊥OD,∴P为AC中点,
又O为圆心,AB为直径∴OP=BC=,
由S△ADC=S△ACB可知DP=BC=1,∴AB=3,从而AC=2 (4分)
(2)①∵GF⊥AC,AG⊥BG,∠ACG=∠ABG
∴∠BAG=∠FGC,又∠CAB=∠CGB=∠AGF,
∴∠CAG=∠CGA,∴CG=AC=2.
设AF=a,由tan∠CAB=tan∠AGF=可知,
FG=2a,AG=3a,∴FC=2-a,
∴(2-a)2+(2a)2=(2)2,
解得a=,从而AG=,∴=. (8分)
②由△AFE∽△ACB,∴,
∴EF=,AE=,∴EG=FG-EF=,EB=
又由①得∠BCH=∠BAG=∠FGC,
∴△BCH∽△EGH,∴,解得BH=. (12分)
同课章节目录
