第二十八章 锐角三角函数 基础闯关卷 (含答案)人教版九年级数学下册
文档属性
| 名称 | 第二十八章 锐角三角函数 基础闯关卷 (含答案)人教版九年级数学下册 |  | |
| 格式 | docx | ||
| 文件大小 | 138.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-03-30 07:55:29 | ||
图片预览

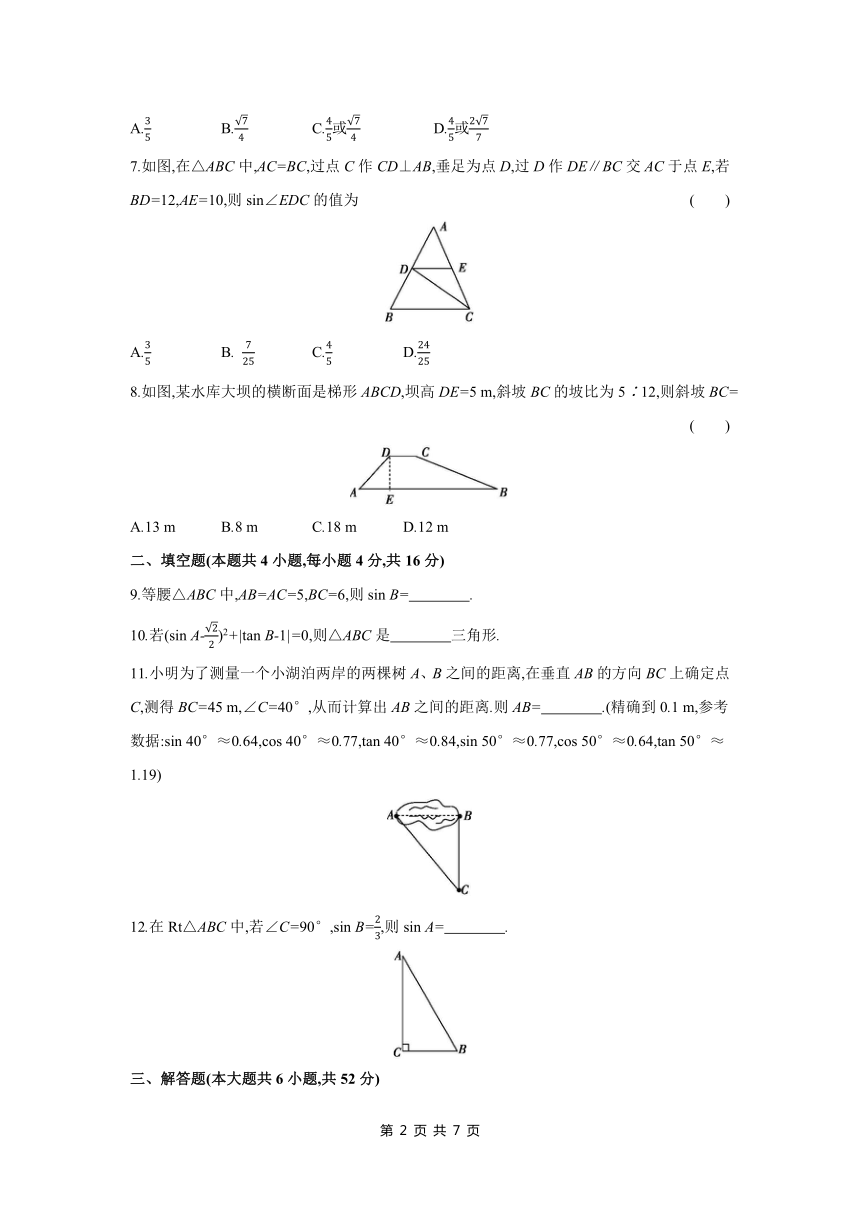
文档简介
第二十八章 锐角三角函数
时间:60分钟 满分:100分
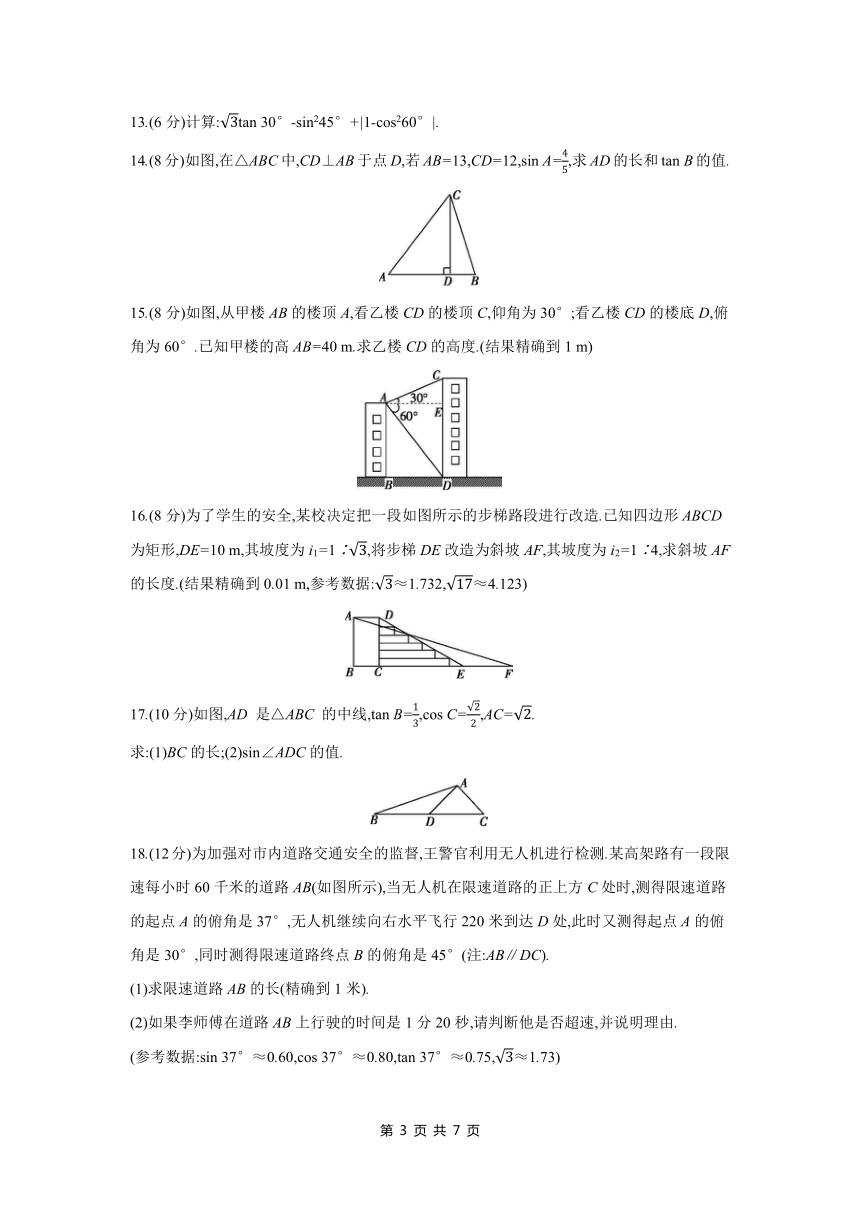
一、选择题(本题共8小题,每小题4分,共32分)
1.tan 45°的值为 ( )
A. B. C.1 D.
2.如图,在地面上的点A处测得树顶B的仰角为α,AC=2,则树高BC为 ( )
A.2sin α B.2cos α C. D.2tan α
3.如图,在△ABC中,∠C=90°,设∠A,∠B,∠C所对的边分别为a,b,c,则下列等式成立的是 ( )
A.c=bsin B B.b=csin B C.a=bcos B D.b=ctan B
4.如图,在3×3的正方形网格中,△ABC的顶点都在格点上,则sin∠CAB= ( )
A. B. C. D.
5.如图,在A处测得点P在北偏东60°方向上,在B处测得点P在北偏东30°方向上,若AB=2米,则点P到直线AB的距离PC为 ( )
A.3米 B.米 C.2米 D.1米
6.在Rt△ABC中,AC=8,BC=6,则cos A的值等于 ( )
A. B. C.或 D.或
7.如图,在△ABC中,AC=BC,过点C作CD⊥AB,垂足为点D,过D作DE∥BC交AC于点E,若BD=12,AE=10,则sin∠EDC的值为 ( )
A. B. C. D.
8.如图,某水库大坝的横断面是梯形ABCD,坝高DE=5 m,斜坡BC的坡比为5∶12,则斜坡BC= ( )
A.13 m B.8 m C.18 m D.12 m
二、填空题(本题共4小题,每小题4分,共16分)
9.等腰△ABC中,AB=AC=5,BC=6,则sin B= .
10.若(sin A-)2+|tan B-1|=0,则△ABC是 三角形.
11.小明为了测量一个小湖泊两岸的两棵树A、B之间的距离,在垂直AB的方向BC上确定点C,测得BC=45 m,∠C=40°,从而计算出AB之间的距离.则AB= .(精确到0.1 m,参考数据:sin 40°≈0.64,cos 40°≈0.77,tan 40°≈0.84,sin 50°≈0.77,cos 50°≈0.64,tan 50°≈1.19)
12.在Rt△ABC中,若∠C=90°,sin B=,则sin A= .
三、解答题(本大题共6小题,共52分)
13.(6分)计算:tan 30°-sin245°+|1-cos260°|.
14.(8分)如图,在△ABC中,CD⊥AB于点D,若AB=13,CD=12,sin A=,求AD的长和tan B的值.
15.(8分)如图,从甲楼AB的楼顶A,看乙楼CD的楼顶C,仰角为30°;看乙楼CD的楼底D,俯角为60°.已知甲楼的高AB=40 m.求乙楼CD的高度.(结果精确到1 m)
16.(8分)为了学生的安全,某校决定把一段如图所示的步梯路段进行改造.已知四边形ABCD为矩形,DE=10 m,其坡度为i1=1∶,将步梯DE改造为斜坡AF,其坡度为i2=1∶4,求斜坡AF的长度.(结果精确到0.01 m,参考数据:≈1.732,≈4.123)
17.(10分)如图,AD 是△ABC 的中线,tan B=,cos C=,AC=.
求:(1)BC的长;(2)sin∠ADC的值.
18.(12分)为加强对市内道路交通安全的监督,王警官利用无人机进行检测.某高架路有一段限速每小时60千米的道路AB(如图所示),当无人机在限速道路的正上方C处时,测得限速道路的起点A的俯角是37°,无人机继续向右水平飞行220米到达D处,此时又测得起点A的俯角是30°,同时测得限速道路终点B的俯角是45°(注:AB∥DC).
(1)求限速道路AB的长(精确到1米).
(2)如果李师傅在道路AB上行驶的时间是1分20秒,请判断他是否超速,并说明理由.
(参考数据:sin 37°≈0.60,cos 37°≈0.80,tan 37°≈0.75,≈1.73)
参考答案
一、选择题
1 2 3 4 5 6 7 8
C D B B B C A A
4.B 【解析】由勾股定理,得AC==,BC==,AB==,∵AB2+BC2=AC2,∴∠ACB=90°,在Rt△ABC中,sin∠BAC===.
5.B 【解析】设点P到直线AB的距离PC为x米,在Rt△APC中,AC==x,在Rt△BPC中,BC==x,由题意得x-x=2,解得x=(米).
6.C 【解析】当△ABC为直角三角形时,存在两种情况:①当AB为斜边,∠C=90°,∵AC=8,BC=6,
∴AB===10.∴cos A===;②当AC为斜边,∠B=90°,由勾股定理得AB===2,
∴cos A===;综上所述,cos A的值等于或.
7.A 【解析】∵AC=BC,CD⊥AB,∴AD=BD=AB,∵DE∥BC,∴==,∴AC=2AE=20,∴AC=BC=20,∵DE∥BC,∴∠EDC=∠DCB,在Rt△BDC中,sin∠DCB===,∴sin∠EDC=.
8.A 【解析】过点C作CF⊥AB于点F,∵DC∥AB,∴CF=DE=5 m,∵斜坡BC的坡比为5∶12,CF=5 m,∴BF=12 m,由勾股定理得BC=13 m.
二、填空题
9 10 11 12
等腰直角 37.8 m
12. 【解析】因为sin B==,所以设AC=2k,AB=3k,则BC==k,所以sin A===.
三、解答题
13.解:原式=×-()2+|1-()2|(3分)
=1-+
=.(6分)
14.解:∵CD⊥AB,∴∠CDA=∠CDB=90°, 在Rt△ACD中,sin A=,
∵sin A=,CD=12,∴=, ∴AC=15,
在Rt△ACD中,由勾股定理得AD===9.(5分)
∴BD=AB-AD=13-9=4,
∴在Rt△BCD中,tan B===3.(8分)
15.解:∵AB⊥BD,CD⊥BD,∴四边形ABDE是矩形,∴DE=AB=40 m,
在Rt△AED中,AE===(m) .(4分)
在Rt△ACE中,CE=AE·tan 30°=×=(m),
∴CD=DE+CE=40+≈53(m).
答:乙楼CD的高约为53 m.(8分)
16.解:∵DE=10 m,其坡度为i1=1∶,
∴在Rt△DCE中,DE==2DC=10 m,∴解得DC=5 m.
∵四边形ABCD为矩形,∴AB=CD=5 m,(3分)
∵斜坡AF的坡度为i2=1∶4,∴=,∴BF=4AB=20 m,
∴在Rt△ABF中,AF==5≈20.62(m).
故斜坡AF的长度约为20.62米.(8分)
17.解:(1)如图,过点A作AE⊥BC于点E.
∵cos C=,∴∠C=45°.
在Rt△ACE中,CE=AC·cos C=1,∴AE=CE=1.
在Rt△ABE中,∵tan B=,∴=,
∴BE=3AE=3,∴BC=BE+CE=3+1=4.(6分)
(2)∵AD是△ABC的中线,∴CD=BC=2.
∴DE=CD-CE=2-1=1.
∵AE⊥BC,∴∠ADC=45°.∴sin∠ADC=.(10分)
18.解:(1)根据题意,得∠CAB=37°,CD=220米,∠DAB=30°,∠DBA=45°,
如图,过点C和点D作CE和DF垂直AB于点E和点F,
∵CD∥AB,∴四边形CDFE是矩形,∴CE=DF,CD=EF,
∵∠DBA=45°,∴DF=BF,设DF=BF=CE=x米,
在Rt△ADF中,∠DAF=30°,DF=x米,
∴AF=DF=x(米),∴AE=AF-EF=(x-220)米.(4分)
在Rt△AEC中,∠CAE=37°,
∵CE=AE·tan 37°,∴x=180+240(米),∴AB=AE+EF+FB=320+240+220+180+240=780+420≈1507(米),
答:限速道路AB的长约为1507米;(8分)
(2)因为1分20秒等于小时,
所以李师傅在道路AB上行驶速度为1507÷1000÷≈67.8 km/h>60 km/h,
所以李师傅超速了.(12分)
时间:60分钟 满分:100分
一、选择题(本题共8小题,每小题4分,共32分)
1.tan 45°的值为 ( )
A. B. C.1 D.
2.如图,在地面上的点A处测得树顶B的仰角为α,AC=2,则树高BC为 ( )
A.2sin α B.2cos α C. D.2tan α
3.如图,在△ABC中,∠C=90°,设∠A,∠B,∠C所对的边分别为a,b,c,则下列等式成立的是 ( )
A.c=bsin B B.b=csin B C.a=bcos B D.b=ctan B
4.如图,在3×3的正方形网格中,△ABC的顶点都在格点上,则sin∠CAB= ( )
A. B. C. D.
5.如图,在A处测得点P在北偏东60°方向上,在B处测得点P在北偏东30°方向上,若AB=2米,则点P到直线AB的距离PC为 ( )
A.3米 B.米 C.2米 D.1米
6.在Rt△ABC中,AC=8,BC=6,则cos A的值等于 ( )
A. B. C.或 D.或
7.如图,在△ABC中,AC=BC,过点C作CD⊥AB,垂足为点D,过D作DE∥BC交AC于点E,若BD=12,AE=10,则sin∠EDC的值为 ( )
A. B. C. D.
8.如图,某水库大坝的横断面是梯形ABCD,坝高DE=5 m,斜坡BC的坡比为5∶12,则斜坡BC= ( )
A.13 m B.8 m C.18 m D.12 m
二、填空题(本题共4小题,每小题4分,共16分)
9.等腰△ABC中,AB=AC=5,BC=6,则sin B= .
10.若(sin A-)2+|tan B-1|=0,则△ABC是 三角形.
11.小明为了测量一个小湖泊两岸的两棵树A、B之间的距离,在垂直AB的方向BC上确定点C,测得BC=45 m,∠C=40°,从而计算出AB之间的距离.则AB= .(精确到0.1 m,参考数据:sin 40°≈0.64,cos 40°≈0.77,tan 40°≈0.84,sin 50°≈0.77,cos 50°≈0.64,tan 50°≈1.19)
12.在Rt△ABC中,若∠C=90°,sin B=,则sin A= .
三、解答题(本大题共6小题,共52分)
13.(6分)计算:tan 30°-sin245°+|1-cos260°|.
14.(8分)如图,在△ABC中,CD⊥AB于点D,若AB=13,CD=12,sin A=,求AD的长和tan B的值.
15.(8分)如图,从甲楼AB的楼顶A,看乙楼CD的楼顶C,仰角为30°;看乙楼CD的楼底D,俯角为60°.已知甲楼的高AB=40 m.求乙楼CD的高度.(结果精确到1 m)
16.(8分)为了学生的安全,某校决定把一段如图所示的步梯路段进行改造.已知四边形ABCD为矩形,DE=10 m,其坡度为i1=1∶,将步梯DE改造为斜坡AF,其坡度为i2=1∶4,求斜坡AF的长度.(结果精确到0.01 m,参考数据:≈1.732,≈4.123)
17.(10分)如图,AD 是△ABC 的中线,tan B=,cos C=,AC=.
求:(1)BC的长;(2)sin∠ADC的值.
18.(12分)为加强对市内道路交通安全的监督,王警官利用无人机进行检测.某高架路有一段限速每小时60千米的道路AB(如图所示),当无人机在限速道路的正上方C处时,测得限速道路的起点A的俯角是37°,无人机继续向右水平飞行220米到达D处,此时又测得起点A的俯角是30°,同时测得限速道路终点B的俯角是45°(注:AB∥DC).
(1)求限速道路AB的长(精确到1米).
(2)如果李师傅在道路AB上行驶的时间是1分20秒,请判断他是否超速,并说明理由.
(参考数据:sin 37°≈0.60,cos 37°≈0.80,tan 37°≈0.75,≈1.73)
参考答案
一、选择题
1 2 3 4 5 6 7 8
C D B B B C A A
4.B 【解析】由勾股定理,得AC==,BC==,AB==,∵AB2+BC2=AC2,∴∠ACB=90°,在Rt△ABC中,sin∠BAC===.
5.B 【解析】设点P到直线AB的距离PC为x米,在Rt△APC中,AC==x,在Rt△BPC中,BC==x,由题意得x-x=2,解得x=(米).
6.C 【解析】当△ABC为直角三角形时,存在两种情况:①当AB为斜边,∠C=90°,∵AC=8,BC=6,
∴AB===10.∴cos A===;②当AC为斜边,∠B=90°,由勾股定理得AB===2,
∴cos A===;综上所述,cos A的值等于或.
7.A 【解析】∵AC=BC,CD⊥AB,∴AD=BD=AB,∵DE∥BC,∴==,∴AC=2AE=20,∴AC=BC=20,∵DE∥BC,∴∠EDC=∠DCB,在Rt△BDC中,sin∠DCB===,∴sin∠EDC=.
8.A 【解析】过点C作CF⊥AB于点F,∵DC∥AB,∴CF=DE=5 m,∵斜坡BC的坡比为5∶12,CF=5 m,∴BF=12 m,由勾股定理得BC=13 m.
二、填空题
9 10 11 12
等腰直角 37.8 m
12. 【解析】因为sin B==,所以设AC=2k,AB=3k,则BC==k,所以sin A===.
三、解答题
13.解:原式=×-()2+|1-()2|(3分)
=1-+
=.(6分)
14.解:∵CD⊥AB,∴∠CDA=∠CDB=90°, 在Rt△ACD中,sin A=,
∵sin A=,CD=12,∴=, ∴AC=15,
在Rt△ACD中,由勾股定理得AD===9.(5分)
∴BD=AB-AD=13-9=4,
∴在Rt△BCD中,tan B===3.(8分)
15.解:∵AB⊥BD,CD⊥BD,∴四边形ABDE是矩形,∴DE=AB=40 m,
在Rt△AED中,AE===(m) .(4分)
在Rt△ACE中,CE=AE·tan 30°=×=(m),
∴CD=DE+CE=40+≈53(m).
答:乙楼CD的高约为53 m.(8分)
16.解:∵DE=10 m,其坡度为i1=1∶,
∴在Rt△DCE中,DE==2DC=10 m,∴解得DC=5 m.
∵四边形ABCD为矩形,∴AB=CD=5 m,(3分)
∵斜坡AF的坡度为i2=1∶4,∴=,∴BF=4AB=20 m,
∴在Rt△ABF中,AF==5≈20.62(m).
故斜坡AF的长度约为20.62米.(8分)
17.解:(1)如图,过点A作AE⊥BC于点E.
∵cos C=,∴∠C=45°.
在Rt△ACE中,CE=AC·cos C=1,∴AE=CE=1.
在Rt△ABE中,∵tan B=,∴=,
∴BE=3AE=3,∴BC=BE+CE=3+1=4.(6分)
(2)∵AD是△ABC的中线,∴CD=BC=2.
∴DE=CD-CE=2-1=1.
∵AE⊥BC,∴∠ADC=45°.∴sin∠ADC=.(10分)
18.解:(1)根据题意,得∠CAB=37°,CD=220米,∠DAB=30°,∠DBA=45°,
如图,过点C和点D作CE和DF垂直AB于点E和点F,
∵CD∥AB,∴四边形CDFE是矩形,∴CE=DF,CD=EF,
∵∠DBA=45°,∴DF=BF,设DF=BF=CE=x米,
在Rt△ADF中,∠DAF=30°,DF=x米,
∴AF=DF=x(米),∴AE=AF-EF=(x-220)米.(4分)
在Rt△AEC中,∠CAE=37°,
∵CE=AE·tan 37°,∴x=180+240(米),∴AB=AE+EF+FB=320+240+220+180+240=780+420≈1507(米),
答:限速道路AB的长约为1507米;(8分)
(2)因为1分20秒等于小时,
所以李师傅在道路AB上行驶速度为1507÷1000÷≈67.8 km/h>60 km/h,
所以李师傅超速了.(12分)
