第二十九章 投影与视图 能力提优卷 (含答案)人教版九年级数学下册
文档属性
| 名称 | 第二十九章 投影与视图 能力提优卷 (含答案)人教版九年级数学下册 |
|
|
| 格式 | docx | ||
| 文件大小 | 138.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-03-30 00:00:00 | ||
图片预览


文档简介
第二十九章 投影与视图
一、选择题(本题共4小题,每小题5分,共20分)
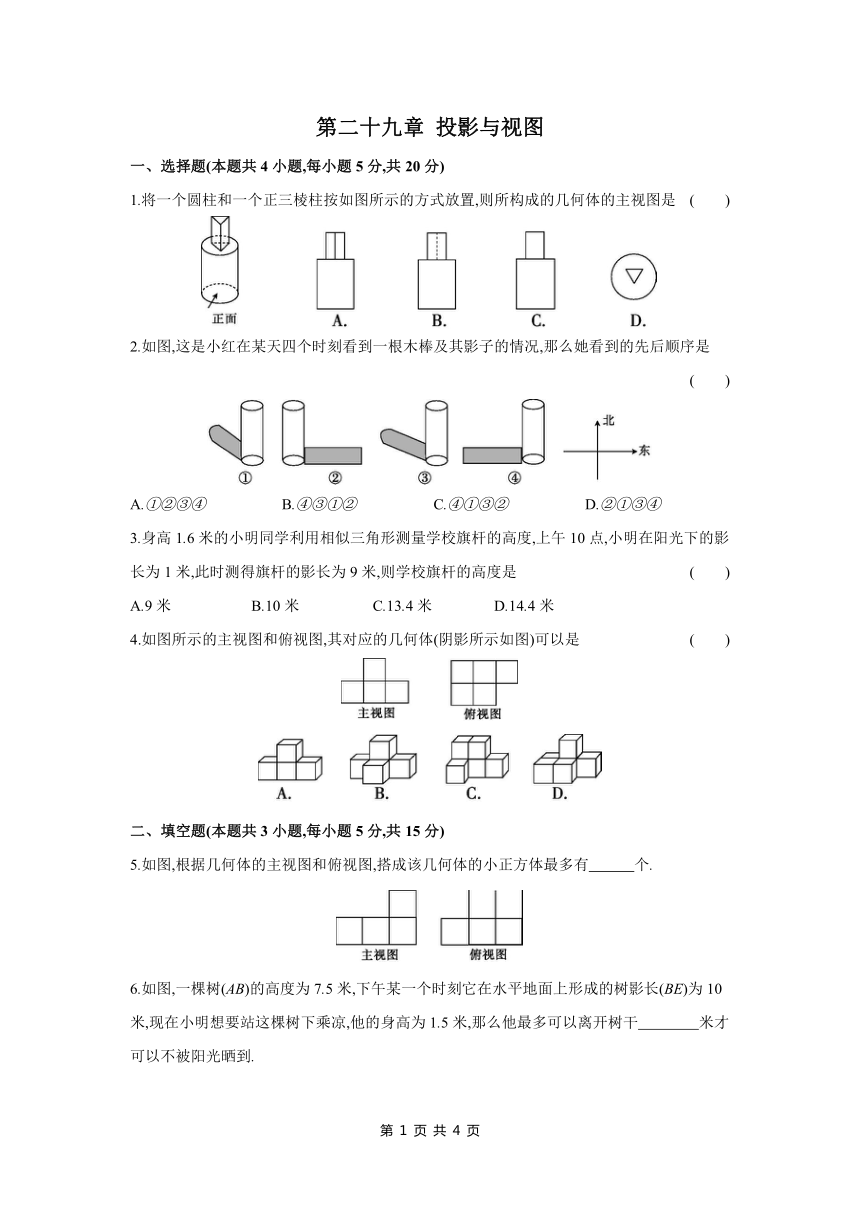
1.将一个圆柱和一个正三棱柱按如图所示的方式放置,则所构成的几何体的主视图是 ( )
2.如图,这是小红在某天四个时刻看到一根木棒及其影子的情况,那么她看到的先后顺序是 ( )
A.①②③④ B.④③①② C.④①③② D.②①③④
3.身高1.6米的小明同学利用相似三角形测量学校旗杆的高度,上午10点,小明在阳光下的影长为1米,此时测得旗杆的影长为9米,则学校旗杆的高度是 ( )
A.9米 B.10米 C.13.4米 D.14.4米
4.如图所示的主视图和俯视图,其对应的几何体(阴影所示如图)可以是 ( )
二、填空题(本题共3小题,每小题5分,共15分)
5.如图,根据几何体的主视图和俯视图,搭成该几何体的小正方体最多有 个.
6.如图,一棵树(AB)的高度为7.5米,下午某一个时刻它在水平地面上形成的树影长(BE)为10米,现在小明想要站这棵树下乘凉,他的身高为1.5米,那么他最多可以离开树干 米才可以不被阳光晒到.
7.张师傅按1∶1的比例画出某直三棱柱零件的三视图,如图所示,已知在△EFG中,EF=12 cm,EG=18 cm,∠EFG=45°,则AB的长为 cm.
三、解答题(本大题共2小题,共15分)
8.(6分)已知一个几何体的三视图如图所示,描述该几何体的形状,并根据图中数据计算它的表面积.(结果精确到1 cm2)
9.(9分)在阳光下,小玲同学测得一根长为1米的垂直地面的竹竿的影长为0.6米,同时小强同学测量树的高度时,发现树的影子有一部分0.2米落在教学楼的第一级台阶上,落在地面上的影长为4.42米,每级台阶高为0.3米.小玲说:“要是没有台阶遮挡的话,树的影子长度应该是4.62米”;小强说:“要是没有台阶遮挡的话,树的影子长度肯定比4.62米要长”.
(1)你认为小玲和小强的说法对吗
(2)请根据小玲和小强的测量数据计算树的高度.
(3)要是没有台阶遮挡的话,树的影子长度是多少米
参考答案
一、选择题
1 2 3 4
A B D D
二、填空题
5 6 7
7 8 6
6.8 【解析】设小明这个时刻在水平地面上形成的影长为x米,根据题意得=,解得x=2,小明这个时刻在水平地面上形成的影长为2米,因为10-2=8(米),所以他最多离开树干8米才可以不被阳光晒到.
7.6 【解析】如图,作EH⊥FG,∵∠EHF=90°,∠EFG=45°,∴∠EFG=∠FEH=45°,∴EH=HF=EF,∵EF=12 cm,∴EH=6,根据三视图的意义可知,AB=EH=6.
三、解答题
8.解:∵有2个视图为长方形,∴该几何体为柱体,
∵第3个视图为直角三角形,
∴该柱体为直三棱柱,(3分)
∵直角三角形斜边长为=30cm,
∴表面积为2××30×30+2×50×30+50×30≈6021 cm2.(6分)
9.解:(1)小玲的说法不对,小强的说法对,理由如下(2)可得;(2分)
(2)根据题意画出图形,如图所示,(4分)
根据平行投影可知=,DE=0.3,∴EH=0.3×0.6=0.18,
∵四边形DGFH是平行四边形,∴FH=DG=0.2,
∵AE=4.42,∴AF=AE+EH+FH=4.42+0.18+0.2=4.8,
∵=,∴AB==8(米).
答:树的高度为8米.(7分)
(3)由(2)可知AF=4.8(米),
答:树的影子长度是4.8米.(9分)
一、选择题(本题共4小题,每小题5分,共20分)
1.将一个圆柱和一个正三棱柱按如图所示的方式放置,则所构成的几何体的主视图是 ( )
2.如图,这是小红在某天四个时刻看到一根木棒及其影子的情况,那么她看到的先后顺序是 ( )
A.①②③④ B.④③①② C.④①③② D.②①③④
3.身高1.6米的小明同学利用相似三角形测量学校旗杆的高度,上午10点,小明在阳光下的影长为1米,此时测得旗杆的影长为9米,则学校旗杆的高度是 ( )
A.9米 B.10米 C.13.4米 D.14.4米
4.如图所示的主视图和俯视图,其对应的几何体(阴影所示如图)可以是 ( )
二、填空题(本题共3小题,每小题5分,共15分)
5.如图,根据几何体的主视图和俯视图,搭成该几何体的小正方体最多有 个.
6.如图,一棵树(AB)的高度为7.5米,下午某一个时刻它在水平地面上形成的树影长(BE)为10米,现在小明想要站这棵树下乘凉,他的身高为1.5米,那么他最多可以离开树干 米才可以不被阳光晒到.
7.张师傅按1∶1的比例画出某直三棱柱零件的三视图,如图所示,已知在△EFG中,EF=12 cm,EG=18 cm,∠EFG=45°,则AB的长为 cm.
三、解答题(本大题共2小题,共15分)
8.(6分)已知一个几何体的三视图如图所示,描述该几何体的形状,并根据图中数据计算它的表面积.(结果精确到1 cm2)
9.(9分)在阳光下,小玲同学测得一根长为1米的垂直地面的竹竿的影长为0.6米,同时小强同学测量树的高度时,发现树的影子有一部分0.2米落在教学楼的第一级台阶上,落在地面上的影长为4.42米,每级台阶高为0.3米.小玲说:“要是没有台阶遮挡的话,树的影子长度应该是4.62米”;小强说:“要是没有台阶遮挡的话,树的影子长度肯定比4.62米要长”.
(1)你认为小玲和小强的说法对吗
(2)请根据小玲和小强的测量数据计算树的高度.
(3)要是没有台阶遮挡的话,树的影子长度是多少米
参考答案
一、选择题
1 2 3 4
A B D D
二、填空题
5 6 7
7 8 6
6.8 【解析】设小明这个时刻在水平地面上形成的影长为x米,根据题意得=,解得x=2,小明这个时刻在水平地面上形成的影长为2米,因为10-2=8(米),所以他最多离开树干8米才可以不被阳光晒到.
7.6 【解析】如图,作EH⊥FG,∵∠EHF=90°,∠EFG=45°,∴∠EFG=∠FEH=45°,∴EH=HF=EF,∵EF=12 cm,∴EH=6,根据三视图的意义可知,AB=EH=6.
三、解答题
8.解:∵有2个视图为长方形,∴该几何体为柱体,
∵第3个视图为直角三角形,
∴该柱体为直三棱柱,(3分)
∵直角三角形斜边长为=30cm,
∴表面积为2××30×30+2×50×30+50×30≈6021 cm2.(6分)
9.解:(1)小玲的说法不对,小强的说法对,理由如下(2)可得;(2分)
(2)根据题意画出图形,如图所示,(4分)
根据平行投影可知=,DE=0.3,∴EH=0.3×0.6=0.18,
∵四边形DGFH是平行四边形,∴FH=DG=0.2,
∵AE=4.42,∴AF=AE+EH+FH=4.42+0.18+0.2=4.8,
∵=,∴AB==8(米).
答:树的高度为8米.(7分)
(3)由(2)可知AF=4.8(米),
答:树的影子长度是4.8米.(9分)
