第二十六章 反比例函数 能力提优卷(含答案) 人教版九年级数学下册
文档属性
| 名称 | 第二十六章 反比例函数 能力提优卷(含答案) 人教版九年级数学下册 |
|
|
| 格式 | docx | ||
| 文件大小 | 175.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-03-30 00:00:00 | ||
图片预览




文档简介
第二十六章 反比例函数
时间:60分钟 满分:100分
一、选择题(本题共8小题,每小题5分,共40分)
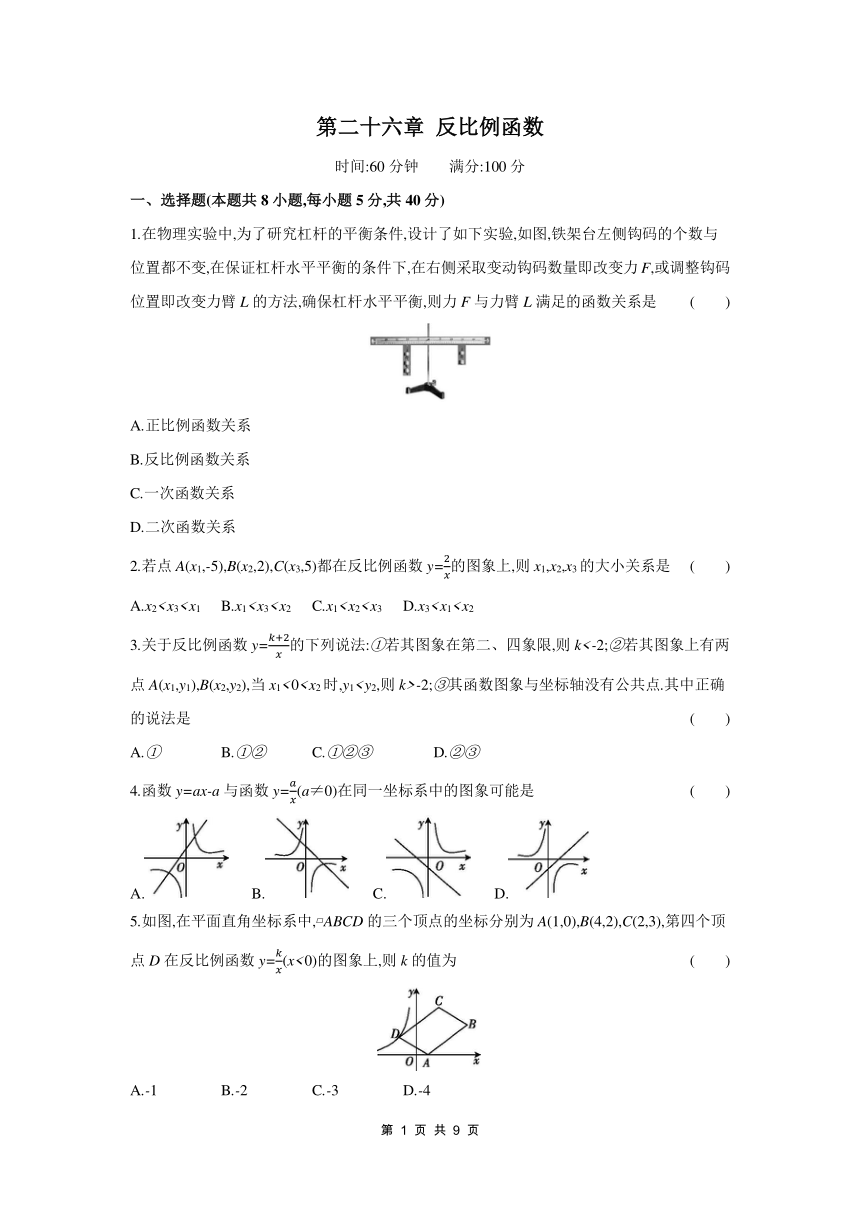
1.在物理实验中,为了研究杠杆的平衡条件,设计了如下实验,如图,铁架台左侧钩码的个数与位置都不变,在保证杠杆水平平衡的条件下,在右侧采取变动钩码数量即改变力F,或调整钩码位置即改变力臂L的方法,确保杠杆水平平衡,则力F与力臂L满足的函数关系是 ( )
A.正比例函数关系
B.反比例函数关系
C.一次函数关系
D.二次函数关系
2.若点A(x1,-5),B(x2,2),C(x3,5)都在反比例函数y=的图象上,则x1,x2,x3的大小关系是 ( )
A.x23.关于反比例函数y=的下列说法:①若其图象在第二、四象限,则k<-2;②若其图象上有两点A(x1,y1),B(x2,y2),当x1<0-2;③其函数图象与坐标轴没有公共点.其中正确的说法是 ( )
A.① B.①② C.①②③ D.②③
4.函数y=ax-a与函数y=(a≠0)在同一坐标系中的图象可能是 ( )
A. B. C. D.
5.如图,在平面直角坐标系中, ABCD的三个顶点的坐标分别为A(1,0),B(4,2),C(2,3),第四个顶点D在反比例函数y=(x<0)的图象上,则k的值为 ( )
A.-1 B.-2 C.-3 D.-4
6.如图,直线l⊥x轴于点P,且与反比例函数y1=(x>0)及y2=(x>0)的图象分别交于点A,B,连接OA,OB,若△OAB的面积为3,则k1-k2= ( )
A. B.3 C.6 D.9
7.在平面直角坐标系中,函数y=kx-1与y=的图象相交,其中有一个交点为P(2,m),点A(x1,y1)在y=kx-1的图象上,点B(x2,y2)在y=的图象上,下列说法正确的是 ( )
A.当x1=x2<2时,y12时,y1C.当y1=y2<1时,x1>x2 D.当y1=y2>1时,x1>x2
8.如图,直线y=kx(k>0)与双曲线y=交于A、B两点,若A、B两点的坐标分别为A(x1,y1),B(x2,y2),则x1y2+x2y1的值为 ( )
A.3 B.-3 C.6 D.-6
二、填空题(本题共4小题,每小题5分,共20分)
9.在照明系统模拟控制电路实验中,研究人员发现光敏电阻值R(单位:Ω)与光照度E(单位:lx)之间成反比例函数关系,部分数据如下表所示:
光照度E/lx 0.5 1 1.5 2 2.5 3
光敏电阻值R/Ω 60 30 20 15 12 10
则光敏电阻值R与光照度E的函数表达式为 .
10.若一次函数y=kx+b(b<0)与反比例函数y=的图象都经过点A(b,3b),则b= .
11.如图,点A,C均在双曲线y=上运动,AB⊥x轴,AC=BC,则△ABC的面积是 .
12.如图,点A,B在反比例函数y=(x>0)的图象上,点C在反比例函数y=(x>0)的图象上,连接AC,BC,且AC∥x轴,BC∥y轴,AC=BC,若点A的横坐标为2,则k的值为 .
三、解答题(本大题共4小题,共40分)
13.(8分)已知点A(2,m+3)在双曲线y=上.
(1)求此双曲线的表达式与点A的坐标.
(2)如果点B(a,5-a)在此双曲线上,图象经过点A、B的一次函数的函数值y随x的增大而增大,求此一次函数的解析式.
14.(10分)已知直线l:y=kx(k≠0)经过点A(-1,2),点P为直线l上一点,其横坐标为m,过点P作y轴的垂线,与函数y=(x>0)的图象交于点Q.
(1)求k的值.
(2)①求点Q的坐标(用含m的式子表示).
②若△POQ的面积大于3,直接写出点P的横坐标m的取值范围.
15.(10分)电灭蚊器的电阻y(kΩ)随温度x(℃)变化的大致图象如图所示,通电后温度由室温10℃上升到30℃时,电阻与温度成反比例函数关系,且在温度达到30℃时,电阻下降到最小值,随后电阻随温度的升高而增加,温度每上升1℃,电阻增加 kΩ.
(1)当10≤x≤30时,求y与x的关系式.
(2)当x=30时,求y的值,并求x>30时,y与x的关系式;
(3)电灭蚊器在使用过程中,温度x在什么范围内时,电阻不超过5 kΩ
16.(12分)如图,反比例函数y=(k≠0)与一次函数y=-x+b的图象在第一象限交于A(1,3)、B(3,1)两点.
(1)求反比例函数和一次函数的解析式.
(2)已知点P(a,0)(a>0),过点P作平行于y轴的直线,在第一象限内交一次函数y=-x+b的图象于点M,交反比例函数y=的图象于点N.若PM>PN,结合函数图象直接写出a的取值范围.
(3)若Q为y轴上的一点,要使QA+QB的值最小,求点Q的坐标.
参考答案
一、选择题
1 2 3 4 5 6 7 8
B B C B A C D D
1.B 【解析】∵要确保杠杆水平平衡,∴力F与力臂L满足的函数关系是反比例函数关系.
2.B 【解析】∵点A(x1,-5),B(x2,2),C(x3,5)都在反比例函数y=的图象上,∴x1=-,x2=1,x3=,∴x13.C 【解析】∵反比例函数的图象在第二、四象限,∴k+2<0,得k<-2,故①正确;∵当x1<00,得k>-2,故②正确;其图象与坐标轴没有公共点,故③正确.
4.B 【解析】A.由函数y=ax-a的图象可知a>0,-a>0,矛盾;B.由函数y=ax-a的图象可知a<0,-a>0,由函数y=(a≠0)的图象可知a<0,一致;C.由函数y=ax-a的图象可知a<0,-a<0,矛盾;D.由函数y=ax-a的图象可知a>0,-a<0,由函数y=(a≠0)的图象可知a<0,矛盾.
5.A 【解析】过点D作DE⊥x轴于点E,CF⊥x轴于点F,作BH∥x轴,交CF于点H,∵A(1,0),B(4,2),C(2,3),∴BH=4-2=2,CH=3-2=1,∵四边形ABCD为平行四边形,∴BC=AD,BC∥AD,∴∠DAB+∠ABC=180°,∵BH∥x轴,∴∠ABH=∠BAF,∵∠DAE+∠BAF+∠DAB=180°=∠CBH+∠ABH+∠DAB,∴∠DAE=∠CBH,∵∠AED=∠BHC=90°,AD=BC,∴△ADE≌△BCH(AAS),∴AE=BH=2,DE=CH=1,∴OE=1,∴D(-1,1),∴k=-1×1=-1.
6.C 【解析】∵反比例函数y1=(x>0)及y2=(x>0)的图象均在第一象限内,∴k1>0,k2>0.∵AP⊥x轴,∴S△OAP=k1,S△OBP=k2,∴S△OAB=S△OAP-S△OBP=(k1-k2)=3,解得k1-k2=6.
7.D 【解析】将点P的坐标代入反比例函数表达式,得m==1,故P(2,1),如图,画直线x=2和y=1,A.当x1=x2<2时,A、B在平行于y轴的直线上,且在直线x=2的左侧,当x<2时, y1、y2的大小不确定,故A错误;B.当x1=x2>2时,A、B在平行于y轴的直线上,且在直线x=2的右侧,从图象看,当x>2时,y1>y2,故B错误;C.当y1=y2<1时,即点A、B在平行于x轴的直线上,且在直线y=1的下方,此时x1、x2的大小不确定,故C错误;D.当y1=y2>1时,即点A、B在平行于x轴的直线上,且在直线y=1的上方,此时x1>x2,故D正确.
8.D 【解析】根据题意得x1y1=x2y2=3,∵点A,B关于原点对称,∴x1=-x2,y1=-y2,∴x1y2+x2y1=-x1y1-x2y2=-3-3=-6.
二、填空题
9 10 11 12
R= - 2 36
9.R= 【解析】由题意得RE=30,则R=.
10.- 【解析】将A(b,3b)代入y=kx+b得3b=k×b+b,∴k=2,将A(b,3b)代入y=,得b=±,∵b<0,∴b=-.
11.2 【解析】如图,过点C作CD⊥AB于点D,CE⊥x轴于点E,设A(a,),C(b,),∴OB=a,OE=b,AB=,CE=,∴BE=OE-OB=b-a.∵CD⊥AB,CE⊥x轴,AB⊥x轴,∴四边形DBEC为矩形,∴BD=CE=,CD=BE=b-a,∵AC=BC,CD⊥AB,∴AB=2BD,∴=2×,∴b=2a,∴S△ABC=AB×CD=××(b-a)=××a=2.
12.36 【解析】当x=2时,y==6,则A(2,6),∵AC∥x轴,∴C点的纵坐标为6,则C(,6),∵BC∥y轴,∴B点的横坐标为,∴B(,),∵CA=CB,∴-2=6-,解得k1=36,k2=12,经检验k1=36,k2=12都为原方程的解,∵当k=12时,点A,B,C重合,∴k=36.
三、解答题
13.解:(1)∵点A(2,m+3)在双曲线y=上,
∴m+3=,解得m=-6,
∴m+3=-3,
∴此双曲线的表达式为y=-, A(2,-3).(3分)
(2)∵点B(a,5-a)在此双曲线y=-上,
∴5-a=-,解得a=-1或a=6,∴点B的坐标为(-1,6)或(6,-1),
由(1)知A(2,-3),
设一次函数的解析式为y=kx+b,
当B的坐标为(-1,6)时,,解得,∴一次函数的解析式为y=-3x+3,
∵k<0,∴一次函数的函数值y随x的增大而减小,不合题意,舍去.
当B的坐标为(6,-1)时,,解得,∴一次函数的解析式为y=x-4,
∵k>0,∴一次函数的函数值y随x的增大而增大,符合题意,
∴一次函数的解析式为y=x-4.(8分)
14.解:(1)将点A的坐标代入y=kx,得2=-k,即k=-2.(2分)
(2)如图.①由(1)知y=-2x,设P(m,-2m),
当-2m=时,x=-,故点Q的坐标为(-,-2m).(5分)
②△POQ的面积=PQ×yP=××>3,
解得m>1或m<-1,由函数y=(x>0),得m<0,
故m<-1.(10分)
15.解:(1)设y=,∴m=xy=10×6=60.
∴当10≤x≤30时,y与x的关系式为y=.(3分)
(2)当x=30时,y==2;
当x>30时,设y=kx+b,
∵函数图象过点(30,2),温度每上升1 ℃,电阻增加 kΩ,∴图象过点(31,),
∴,解得,
故x>30时,y与x的关系式为y=x-6.(8分)
(3)当y=5时,5=,解得x=12;5=x-6,解得x=.
答:温度x的取值范围是12≤x≤.(10分)
16.解:(1)根据题意得3=,3=-1+b,∴k=3,b=4,
∴反比例函数和一次函数的解析式分别为y=,y=-x+4.(4分)
(2)由图象得,当PM>PN时,1(3)∵A(1,3),∴A关于y轴的对称点A'的坐标为(-1,3),如图,A'B为QA+QB的最小值,
设直线A'B的解析式为y=mx+n,
∴,解得,
∴直线A'B的解析式为y=-x+,
令x=0,则y=,∴Q(0,).(12分)
时间:60分钟 满分:100分
一、选择题(本题共8小题,每小题5分,共40分)
1.在物理实验中,为了研究杠杆的平衡条件,设计了如下实验,如图,铁架台左侧钩码的个数与位置都不变,在保证杠杆水平平衡的条件下,在右侧采取变动钩码数量即改变力F,或调整钩码位置即改变力臂L的方法,确保杠杆水平平衡,则力F与力臂L满足的函数关系是 ( )
A.正比例函数关系
B.反比例函数关系
C.一次函数关系
D.二次函数关系
2.若点A(x1,-5),B(x2,2),C(x3,5)都在反比例函数y=的图象上,则x1,x2,x3的大小关系是 ( )
A.x2
A.① B.①② C.①②③ D.②③
4.函数y=ax-a与函数y=(a≠0)在同一坐标系中的图象可能是 ( )
A. B. C. D.
5.如图,在平面直角坐标系中, ABCD的三个顶点的坐标分别为A(1,0),B(4,2),C(2,3),第四个顶点D在反比例函数y=(x<0)的图象上,则k的值为 ( )
A.-1 B.-2 C.-3 D.-4
6.如图,直线l⊥x轴于点P,且与反比例函数y1=(x>0)及y2=(x>0)的图象分别交于点A,B,连接OA,OB,若△OAB的面积为3,则k1-k2= ( )
A. B.3 C.6 D.9
7.在平面直角坐标系中,函数y=kx-1与y=的图象相交,其中有一个交点为P(2,m),点A(x1,y1)在y=kx-1的图象上,点B(x2,y2)在y=的图象上,下列说法正确的是 ( )
A.当x1=x2<2时,y1
8.如图,直线y=kx(k>0)与双曲线y=交于A、B两点,若A、B两点的坐标分别为A(x1,y1),B(x2,y2),则x1y2+x2y1的值为 ( )
A.3 B.-3 C.6 D.-6
二、填空题(本题共4小题,每小题5分,共20分)
9.在照明系统模拟控制电路实验中,研究人员发现光敏电阻值R(单位:Ω)与光照度E(单位:lx)之间成反比例函数关系,部分数据如下表所示:
光照度E/lx 0.5 1 1.5 2 2.5 3
光敏电阻值R/Ω 60 30 20 15 12 10
则光敏电阻值R与光照度E的函数表达式为 .
10.若一次函数y=kx+b(b<0)与反比例函数y=的图象都经过点A(b,3b),则b= .
11.如图,点A,C均在双曲线y=上运动,AB⊥x轴,AC=BC,则△ABC的面积是 .
12.如图,点A,B在反比例函数y=(x>0)的图象上,点C在反比例函数y=(x>0)的图象上,连接AC,BC,且AC∥x轴,BC∥y轴,AC=BC,若点A的横坐标为2,则k的值为 .
三、解答题(本大题共4小题,共40分)
13.(8分)已知点A(2,m+3)在双曲线y=上.
(1)求此双曲线的表达式与点A的坐标.
(2)如果点B(a,5-a)在此双曲线上,图象经过点A、B的一次函数的函数值y随x的增大而增大,求此一次函数的解析式.
14.(10分)已知直线l:y=kx(k≠0)经过点A(-1,2),点P为直线l上一点,其横坐标为m,过点P作y轴的垂线,与函数y=(x>0)的图象交于点Q.
(1)求k的值.
(2)①求点Q的坐标(用含m的式子表示).
②若△POQ的面积大于3,直接写出点P的横坐标m的取值范围.
15.(10分)电灭蚊器的电阻y(kΩ)随温度x(℃)变化的大致图象如图所示,通电后温度由室温10℃上升到30℃时,电阻与温度成反比例函数关系,且在温度达到30℃时,电阻下降到最小值,随后电阻随温度的升高而增加,温度每上升1℃,电阻增加 kΩ.
(1)当10≤x≤30时,求y与x的关系式.
(2)当x=30时,求y的值,并求x>30时,y与x的关系式;
(3)电灭蚊器在使用过程中,温度x在什么范围内时,电阻不超过5 kΩ
16.(12分)如图,反比例函数y=(k≠0)与一次函数y=-x+b的图象在第一象限交于A(1,3)、B(3,1)两点.
(1)求反比例函数和一次函数的解析式.
(2)已知点P(a,0)(a>0),过点P作平行于y轴的直线,在第一象限内交一次函数y=-x+b的图象于点M,交反比例函数y=的图象于点N.若PM>PN,结合函数图象直接写出a的取值范围.
(3)若Q为y轴上的一点,要使QA+QB的值最小,求点Q的坐标.
参考答案
一、选择题
1 2 3 4 5 6 7 8
B B C B A C D D
1.B 【解析】∵要确保杠杆水平平衡,∴力F与力臂L满足的函数关系是反比例函数关系.
2.B 【解析】∵点A(x1,-5),B(x2,2),C(x3,5)都在反比例函数y=的图象上,∴x1=-,x2=1,x3=,∴x1
4.B 【解析】A.由函数y=ax-a的图象可知a>0,-a>0,矛盾;B.由函数y=ax-a的图象可知a<0,-a>0,由函数y=(a≠0)的图象可知a<0,一致;C.由函数y=ax-a的图象可知a<0,-a<0,矛盾;D.由函数y=ax-a的图象可知a>0,-a<0,由函数y=(a≠0)的图象可知a<0,矛盾.
5.A 【解析】过点D作DE⊥x轴于点E,CF⊥x轴于点F,作BH∥x轴,交CF于点H,∵A(1,0),B(4,2),C(2,3),∴BH=4-2=2,CH=3-2=1,∵四边形ABCD为平行四边形,∴BC=AD,BC∥AD,∴∠DAB+∠ABC=180°,∵BH∥x轴,∴∠ABH=∠BAF,∵∠DAE+∠BAF+∠DAB=180°=∠CBH+∠ABH+∠DAB,∴∠DAE=∠CBH,∵∠AED=∠BHC=90°,AD=BC,∴△ADE≌△BCH(AAS),∴AE=BH=2,DE=CH=1,∴OE=1,∴D(-1,1),∴k=-1×1=-1.
6.C 【解析】∵反比例函数y1=(x>0)及y2=(x>0)的图象均在第一象限内,∴k1>0,k2>0.∵AP⊥x轴,∴S△OAP=k1,S△OBP=k2,∴S△OAB=S△OAP-S△OBP=(k1-k2)=3,解得k1-k2=6.
7.D 【解析】将点P的坐标代入反比例函数表达式,得m==1,故P(2,1),如图,画直线x=2和y=1,A.当x1=x2<2时,A、B在平行于y轴的直线上,且在直线x=2的左侧,当x<2时, y1、y2的大小不确定,故A错误;B.当x1=x2>2时,A、B在平行于y轴的直线上,且在直线x=2的右侧,从图象看,当x>2时,y1>y2,故B错误;C.当y1=y2<1时,即点A、B在平行于x轴的直线上,且在直线y=1的下方,此时x1、x2的大小不确定,故C错误;D.当y1=y2>1时,即点A、B在平行于x轴的直线上,且在直线y=1的上方,此时x1>x2,故D正确.
8.D 【解析】根据题意得x1y1=x2y2=3,∵点A,B关于原点对称,∴x1=-x2,y1=-y2,∴x1y2+x2y1=-x1y1-x2y2=-3-3=-6.
二、填空题
9 10 11 12
R= - 2 36
9.R= 【解析】由题意得RE=30,则R=.
10.- 【解析】将A(b,3b)代入y=kx+b得3b=k×b+b,∴k=2,将A(b,3b)代入y=,得b=±,∵b<0,∴b=-.
11.2 【解析】如图,过点C作CD⊥AB于点D,CE⊥x轴于点E,设A(a,),C(b,),∴OB=a,OE=b,AB=,CE=,∴BE=OE-OB=b-a.∵CD⊥AB,CE⊥x轴,AB⊥x轴,∴四边形DBEC为矩形,∴BD=CE=,CD=BE=b-a,∵AC=BC,CD⊥AB,∴AB=2BD,∴=2×,∴b=2a,∴S△ABC=AB×CD=××(b-a)=××a=2.
12.36 【解析】当x=2时,y==6,则A(2,6),∵AC∥x轴,∴C点的纵坐标为6,则C(,6),∵BC∥y轴,∴B点的横坐标为,∴B(,),∵CA=CB,∴-2=6-,解得k1=36,k2=12,经检验k1=36,k2=12都为原方程的解,∵当k=12时,点A,B,C重合,∴k=36.
三、解答题
13.解:(1)∵点A(2,m+3)在双曲线y=上,
∴m+3=,解得m=-6,
∴m+3=-3,
∴此双曲线的表达式为y=-, A(2,-3).(3分)
(2)∵点B(a,5-a)在此双曲线y=-上,
∴5-a=-,解得a=-1或a=6,∴点B的坐标为(-1,6)或(6,-1),
由(1)知A(2,-3),
设一次函数的解析式为y=kx+b,
当B的坐标为(-1,6)时,,解得,∴一次函数的解析式为y=-3x+3,
∵k<0,∴一次函数的函数值y随x的增大而减小,不合题意,舍去.
当B的坐标为(6,-1)时,,解得,∴一次函数的解析式为y=x-4,
∵k>0,∴一次函数的函数值y随x的增大而增大,符合题意,
∴一次函数的解析式为y=x-4.(8分)
14.解:(1)将点A的坐标代入y=kx,得2=-k,即k=-2.(2分)
(2)如图.①由(1)知y=-2x,设P(m,-2m),
当-2m=时,x=-,故点Q的坐标为(-,-2m).(5分)
②△POQ的面积=PQ×yP=××>3,
解得m>1或m<-1,由函数y=(x>0),得m<0,
故m<-1.(10分)
15.解:(1)设y=,∴m=xy=10×6=60.
∴当10≤x≤30时,y与x的关系式为y=.(3分)
(2)当x=30时,y==2;
当x>30时,设y=kx+b,
∵函数图象过点(30,2),温度每上升1 ℃,电阻增加 kΩ,∴图象过点(31,),
∴,解得,
故x>30时,y与x的关系式为y=x-6.(8分)
(3)当y=5时,5=,解得x=12;5=x-6,解得x=.
答:温度x的取值范围是12≤x≤.(10分)
16.解:(1)根据题意得3=,3=-1+b,∴k=3,b=4,
∴反比例函数和一次函数的解析式分别为y=,y=-x+4.(4分)
(2)由图象得,当PM>PN时,1
设直线A'B的解析式为y=mx+n,
∴,解得,
∴直线A'B的解析式为y=-x+,
令x=0,则y=,∴Q(0,).(12分)
