第二十七章 相似 基础闯关卷 (含答案)人教版九年级数学下册
文档属性
| 名称 | 第二十七章 相似 基础闯关卷 (含答案)人教版九年级数学下册 |  | |
| 格式 | docx | ||
| 文件大小 | 219.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-03-30 07:57:50 | ||
图片预览

文档简介
第二十七章 相似
时间:60分钟 满分:100分
一、选择题(本题共8小题,每小题4分,共32分)
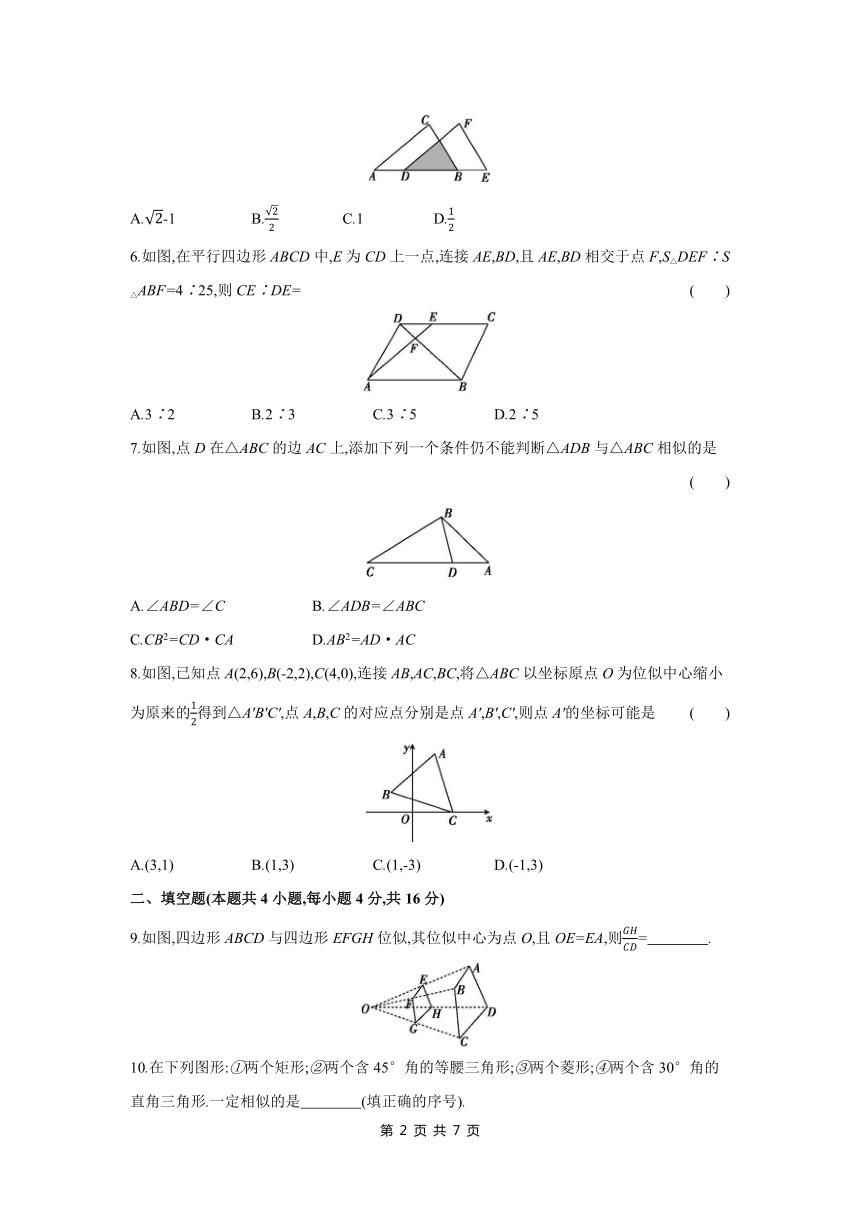
1.如图,在△ABC中,DE∥BC,若AD=2,AB=3,则等于 ( )
A. B. C. D.
2.如图所示的4×4的正方形网格中,小正方形的边长均为1,三角形的顶点都在格点上.相似的三角形是 ( )
A.①和② B.①和③ C.②和③ D.②和④
3.如图,小明在地面上放了一个平面镜,选择合适的位置,刚好在平面镜中看到旗杆的顶部,此时小明与平面镜的水平距离为2米,旗杆底部与平面镜的水平距离为16米,若小明的眼睛与地面距离为1.5米,则旗杆的高度为 ( )
A.米 B.12米 C.9米 D.米
4.如图,在平行四边形ABCD中,点E,F分别为AB,BC的中点,则三角形BEF与多边形EFCDA的面积之比为 ( )
A.1∶4 B.1∶5 C.1∶7 D.1∶8
5.如图,把△ABC沿AB边平移到△DEF的位置,它们重叠部分的面积是△ABC面积的一半,若AB=,则此三角形移动的距离是 ( )
A.-1 B. C.1 D.
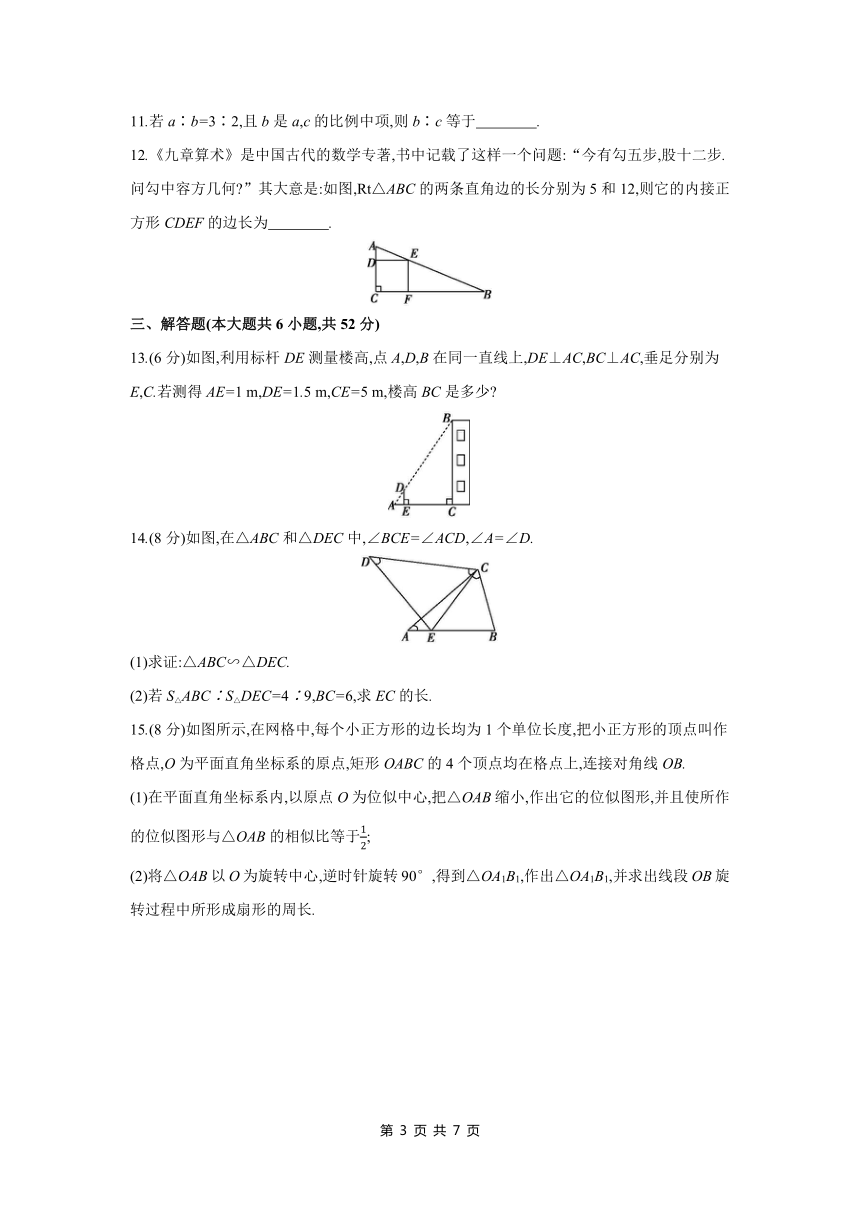
6.如图,在平行四边形ABCD中,E为CD上一点,连接AE,BD,且AE,BD相交于点F,S△DEF∶S△ABF=4∶25,则CE∶DE= ( )
A.3∶2 B.2∶3 C.3∶5 D.2∶5
7.如图,点D在△ABC的边AC上,添加下列一个条件仍不能判断△ADB与△ABC相似的是 ( )
A.∠ABD=∠C B.∠ADB=∠ABC
C.CB2=CD·CA D.AB2=AD·AC
8.如图,已知点A(2,6),B(-2,2),C(4,0),连接AB,AC,BC,将△ABC以坐标原点O为位似中心缩小为原来的得到△A'B'C',点A,B,C的对应点分别是点A',B',C',则点A'的坐标可能是 ( )
A.(3,1) B.(1,3) C.(1,-3) D.(-1,3)
二、填空题(本题共4小题,每小题4分,共16分)
9.如图,四边形ABCD与四边形EFGH位似,其位似中心为点O,且OE=EA,则= .
10.在下列图形:①两个矩形;②两个含45°角的等腰三角形;③两个菱形;④两个含30°角的直角三角形.一定相似的是 (填正确的序号).
11.若a∶b=3∶2,且b是a,c的比例中项,则b∶c等于 .
12.《九章算术》是中国古代的数学专著,书中记载了这样一个问题:“今有勾五步,股十二步.问勾中容方几何 ”其大意是:如图,Rt△ABC的两条直角边的长分别为5和12,则它的内接正方形CDEF的边长为 .
三、解答题(本大题共6小题,共52分)
13.(6分)如图,利用标杆DE测量楼高,点A,D,B在同一直线上,DE⊥AC,BC⊥AC,垂足分别为E,C.若测得AE=1 m,DE=1.5 m,CE=5 m,楼高BC是多少
14.(8分)如图,在△ABC和△DEC中,∠BCE=∠ACD,∠A=∠D.
(1)求证:△ABC∽△DEC.
(2)若S△ABC∶S△DEC=4∶9,BC=6,求EC的长.
15.(8分)如图所示,在网格中,每个小正方形的边长均为1个单位长度,把小正方形的顶点叫作格点,O为平面直角坐标系的原点,矩形OABC的4个顶点均在格点上,连接对角线OB.
(1)在平面直角坐标系内,以原点O为位似中心,把△OAB缩小,作出它的位似图形,并且使所作的位似图形与△OAB的相似比等于;
(2)将△OAB以O为旋转中心,逆时针旋转90°,得到△OA1B1,作出△OA1B1,并求出线段OB旋转过程中所形成扇形的周长.
16.(8分)如图,在菱形ABCD中,对角线AC与BD相交于点O,AC=4,BD=8,点E在边AD上,AE=AD,连接BE交AC于点M.
(1)求AM的长;(2)tan∠MBO的值为 .
17.(10分)如图,在△ABC中,点D,E,F分别在AB,BC,AC边上,DE∥AC,EF∥AB.
(1)求证:△BDE∽△EFC.
(2)设=,①若BC=12,求线段BE的长.②若△EFC的面积是20,求△ABC的面积.
18.(12分)如图,在 ABCD中,点E、F分别在边AD、BC上,且∠ABE=∠CDF.
(1)探究四边形BEDF的形状,并说明理由;
(2)连接AC,分别交BE、DF于点G、H,连接BD交AC于点O.若=,AE=4,求BC的长.
参考答案
一、选择题
1 2 3 4 5 6 7 8
D B B C A A C B
4.C 【解析】连接AC,∵点E,F分别为AB,BC的中点,∴EF是△BAC的中位线,∴EF∥AC,EF=AC,∴△BEF∽△BAC,∴S△BEF∶S△BAC=1∶4,∴S△BEF∶S四边形AEFC=1∶3,∵四边形ABCD是平行四边形,∵S△ABC=S△ADC,∴三角形BEF与多边形EFCDA的面积之比=1∶7.
5.A 【解析】∵△ABC沿AB边平移到△DEF的位置,∴AC∥DF,∴△ABC∽△DBG,∴=()2=,∴AB∶DB=∶1,∵AB=,∴DB=1,∴AD=-1.
6.A 【解析】∵四边形ABCD为平行四边形,∴DE∥AB,∴△DEF∽△BAF,∴=()2=,∴=,∴CE∶DE=3∶2.
7.C 【解析】∵∠A是公共角,∴当∠ABD=∠C或∠ADB=∠ABC时,△ADB∽△ABC(有两角对应相等的三角形相似),故A与B正确;当=,即AB2=AD·AC时,△ADB∽△ABC(两组对应边的比相等且夹角对应相等的两个三角形相似),故D正确;当CB2=CD·CA时,∠A不是夹角,故不能判定△ADB与△ABC相似,故C错误.
8.B 【解析】∵将△ABC以坐标原点O为位似中心缩小为原来的得到△A'B'C',点A的坐标为(2,6),∴点A'的坐标是(2×,6×)或(-2×,-6×),即(1,3)或(-1,-3),∴点A'的坐标可能是(1,3).
二、填空题
9 10 11 12
④ 3∶2
11.3∶2 【解析】∵b是a、c的比例中项,∴b2=ac,即=,∵a∶b=3∶2,∴b∶c=3∶2.
12. 【解析】设正方形CDEF边长为x,则CD=DE=x,由Rt△ABC的两条直角边的长分别为5和12可知AC=5,AD=5-x,BC=12,∵正方形CDEF,∴DE∥BC,∴∠ADE=∠ACB,又∠A=∠A,∴△ADE∽△ACB,∴=,即=,解得x=.
三、解答题
13.解:∵DE⊥AC,BC⊥AC,∴DE∥BC,∴△ADE∽△ABC,(3分)
∴=,∴=,∴BC=9 m.
答:楼高BC是9 m.(6分)
14.(1)证明:∵∠BCE=∠ACD,
∴∠BCE+∠ACE=∠ACD+∠ACE,即∠DCE=∠ACB,
又∵∠A=∠D,∴△ABC∽△DEC;(4分)
(2)∵△ABC∽△DEC,∴=()2=,∴=,
又∵BC=6,∴CE=9.(8分)
15.解:(1)如图,△OA'B'或△OA''B''即为所求.
(4分)
(2)如图,△OA1B1即为所求.OB==2,
线段OB旋转过程中所形成扇形的周长=2×2+=4+π.(8分)
16.解:(1)在菱形ABCD中,AD∥BC,AD=BC,
∴△AEM∽△CBM,∴=,
∵AE=AD,∴AE=BC,
∴==,∴AM=CM=AC=1.(4分)
(2)∵AO=AC=2,BO=BD=4,AC⊥BD,
∴∠BOM=90°,AM=OM=AO=1,
∴tan∠MBO==.(8分)
17.解: (1)证明:∵DE∥AC,∴∠BED=∠C.
∵EF∥AB,∴∠B=∠FEC,∴△BDE∽△EFC.(3分)
(2)①∵EF∥AB,DE∥AC,∴AF=DE,∴==.
∵BC=12,∴=,∴BE=4.(6分)
②∵EF∥AB,∴∠B=∠FEC,∠C=∠C,∴△EFC∽△BAC,∴=()2.
∵=,∴=.又∵△EFC的面积是20,
∴=()2,∴S△ABC=45,即△ABC的面积是45.(10分)
18.解:(1)四边形BEDF为平行四边形,理由如下:
∵四边形ABCD为平行四边形,∴∠ABC=∠ADC,
∵∠ABE=∠CDF,∴∠EBF=∠EDF,
∵四边形ABCD为平行四边形,∴AD∥BC,
∴∠EDF=∠DFC=∠EBF,∴BE∥DF,
∵AD∥BC,∴四边形BEDF为平行四边形;(6分)
(2)设AG=2a,∵=,∴OG=3a,AO=5a,
∵四边形ABCD为平行四边形,∴AO=CO=5a,AC=10a,CG=8a,
∵AD∥BC,∴△AGE∽△CGB,∴==,
∵AE=4,∴BC=16.(12分)
时间:60分钟 满分:100分
一、选择题(本题共8小题,每小题4分,共32分)
1.如图,在△ABC中,DE∥BC,若AD=2,AB=3,则等于 ( )
A. B. C. D.
2.如图所示的4×4的正方形网格中,小正方形的边长均为1,三角形的顶点都在格点上.相似的三角形是 ( )
A.①和② B.①和③ C.②和③ D.②和④
3.如图,小明在地面上放了一个平面镜,选择合适的位置,刚好在平面镜中看到旗杆的顶部,此时小明与平面镜的水平距离为2米,旗杆底部与平面镜的水平距离为16米,若小明的眼睛与地面距离为1.5米,则旗杆的高度为 ( )
A.米 B.12米 C.9米 D.米
4.如图,在平行四边形ABCD中,点E,F分别为AB,BC的中点,则三角形BEF与多边形EFCDA的面积之比为 ( )
A.1∶4 B.1∶5 C.1∶7 D.1∶8
5.如图,把△ABC沿AB边平移到△DEF的位置,它们重叠部分的面积是△ABC面积的一半,若AB=,则此三角形移动的距离是 ( )
A.-1 B. C.1 D.
6.如图,在平行四边形ABCD中,E为CD上一点,连接AE,BD,且AE,BD相交于点F,S△DEF∶S△ABF=4∶25,则CE∶DE= ( )
A.3∶2 B.2∶3 C.3∶5 D.2∶5
7.如图,点D在△ABC的边AC上,添加下列一个条件仍不能判断△ADB与△ABC相似的是 ( )
A.∠ABD=∠C B.∠ADB=∠ABC
C.CB2=CD·CA D.AB2=AD·AC
8.如图,已知点A(2,6),B(-2,2),C(4,0),连接AB,AC,BC,将△ABC以坐标原点O为位似中心缩小为原来的得到△A'B'C',点A,B,C的对应点分别是点A',B',C',则点A'的坐标可能是 ( )
A.(3,1) B.(1,3) C.(1,-3) D.(-1,3)
二、填空题(本题共4小题,每小题4分,共16分)
9.如图,四边形ABCD与四边形EFGH位似,其位似中心为点O,且OE=EA,则= .
10.在下列图形:①两个矩形;②两个含45°角的等腰三角形;③两个菱形;④两个含30°角的直角三角形.一定相似的是 (填正确的序号).
11.若a∶b=3∶2,且b是a,c的比例中项,则b∶c等于 .
12.《九章算术》是中国古代的数学专著,书中记载了这样一个问题:“今有勾五步,股十二步.问勾中容方几何 ”其大意是:如图,Rt△ABC的两条直角边的长分别为5和12,则它的内接正方形CDEF的边长为 .
三、解答题(本大题共6小题,共52分)
13.(6分)如图,利用标杆DE测量楼高,点A,D,B在同一直线上,DE⊥AC,BC⊥AC,垂足分别为E,C.若测得AE=1 m,DE=1.5 m,CE=5 m,楼高BC是多少
14.(8分)如图,在△ABC和△DEC中,∠BCE=∠ACD,∠A=∠D.
(1)求证:△ABC∽△DEC.
(2)若S△ABC∶S△DEC=4∶9,BC=6,求EC的长.
15.(8分)如图所示,在网格中,每个小正方形的边长均为1个单位长度,把小正方形的顶点叫作格点,O为平面直角坐标系的原点,矩形OABC的4个顶点均在格点上,连接对角线OB.
(1)在平面直角坐标系内,以原点O为位似中心,把△OAB缩小,作出它的位似图形,并且使所作的位似图形与△OAB的相似比等于;
(2)将△OAB以O为旋转中心,逆时针旋转90°,得到△OA1B1,作出△OA1B1,并求出线段OB旋转过程中所形成扇形的周长.
16.(8分)如图,在菱形ABCD中,对角线AC与BD相交于点O,AC=4,BD=8,点E在边AD上,AE=AD,连接BE交AC于点M.
(1)求AM的长;(2)tan∠MBO的值为 .
17.(10分)如图,在△ABC中,点D,E,F分别在AB,BC,AC边上,DE∥AC,EF∥AB.
(1)求证:△BDE∽△EFC.
(2)设=,①若BC=12,求线段BE的长.②若△EFC的面积是20,求△ABC的面积.
18.(12分)如图,在 ABCD中,点E、F分别在边AD、BC上,且∠ABE=∠CDF.
(1)探究四边形BEDF的形状,并说明理由;
(2)连接AC,分别交BE、DF于点G、H,连接BD交AC于点O.若=,AE=4,求BC的长.
参考答案
一、选择题
1 2 3 4 5 6 7 8
D B B C A A C B
4.C 【解析】连接AC,∵点E,F分别为AB,BC的中点,∴EF是△BAC的中位线,∴EF∥AC,EF=AC,∴△BEF∽△BAC,∴S△BEF∶S△BAC=1∶4,∴S△BEF∶S四边形AEFC=1∶3,∵四边形ABCD是平行四边形,∵S△ABC=S△ADC,∴三角形BEF与多边形EFCDA的面积之比=1∶7.
5.A 【解析】∵△ABC沿AB边平移到△DEF的位置,∴AC∥DF,∴△ABC∽△DBG,∴=()2=,∴AB∶DB=∶1,∵AB=,∴DB=1,∴AD=-1.
6.A 【解析】∵四边形ABCD为平行四边形,∴DE∥AB,∴△DEF∽△BAF,∴=()2=,∴=,∴CE∶DE=3∶2.
7.C 【解析】∵∠A是公共角,∴当∠ABD=∠C或∠ADB=∠ABC时,△ADB∽△ABC(有两角对应相等的三角形相似),故A与B正确;当=,即AB2=AD·AC时,△ADB∽△ABC(两组对应边的比相等且夹角对应相等的两个三角形相似),故D正确;当CB2=CD·CA时,∠A不是夹角,故不能判定△ADB与△ABC相似,故C错误.
8.B 【解析】∵将△ABC以坐标原点O为位似中心缩小为原来的得到△A'B'C',点A的坐标为(2,6),∴点A'的坐标是(2×,6×)或(-2×,-6×),即(1,3)或(-1,-3),∴点A'的坐标可能是(1,3).
二、填空题
9 10 11 12
④ 3∶2
11.3∶2 【解析】∵b是a、c的比例中项,∴b2=ac,即=,∵a∶b=3∶2,∴b∶c=3∶2.
12. 【解析】设正方形CDEF边长为x,则CD=DE=x,由Rt△ABC的两条直角边的长分别为5和12可知AC=5,AD=5-x,BC=12,∵正方形CDEF,∴DE∥BC,∴∠ADE=∠ACB,又∠A=∠A,∴△ADE∽△ACB,∴=,即=,解得x=.
三、解答题
13.解:∵DE⊥AC,BC⊥AC,∴DE∥BC,∴△ADE∽△ABC,(3分)
∴=,∴=,∴BC=9 m.
答:楼高BC是9 m.(6分)
14.(1)证明:∵∠BCE=∠ACD,
∴∠BCE+∠ACE=∠ACD+∠ACE,即∠DCE=∠ACB,
又∵∠A=∠D,∴△ABC∽△DEC;(4分)
(2)∵△ABC∽△DEC,∴=()2=,∴=,
又∵BC=6,∴CE=9.(8分)
15.解:(1)如图,△OA'B'或△OA''B''即为所求.
(4分)
(2)如图,△OA1B1即为所求.OB==2,
线段OB旋转过程中所形成扇形的周长=2×2+=4+π.(8分)
16.解:(1)在菱形ABCD中,AD∥BC,AD=BC,
∴△AEM∽△CBM,∴=,
∵AE=AD,∴AE=BC,
∴==,∴AM=CM=AC=1.(4分)
(2)∵AO=AC=2,BO=BD=4,AC⊥BD,
∴∠BOM=90°,AM=OM=AO=1,
∴tan∠MBO==.(8分)
17.解: (1)证明:∵DE∥AC,∴∠BED=∠C.
∵EF∥AB,∴∠B=∠FEC,∴△BDE∽△EFC.(3分)
(2)①∵EF∥AB,DE∥AC,∴AF=DE,∴==.
∵BC=12,∴=,∴BE=4.(6分)
②∵EF∥AB,∴∠B=∠FEC,∠C=∠C,∴△EFC∽△BAC,∴=()2.
∵=,∴=.又∵△EFC的面积是20,
∴=()2,∴S△ABC=45,即△ABC的面积是45.(10分)
18.解:(1)四边形BEDF为平行四边形,理由如下:
∵四边形ABCD为平行四边形,∴∠ABC=∠ADC,
∵∠ABE=∠CDF,∴∠EBF=∠EDF,
∵四边形ABCD为平行四边形,∴AD∥BC,
∴∠EDF=∠DFC=∠EBF,∴BE∥DF,
∵AD∥BC,∴四边形BEDF为平行四边形;(6分)
(2)设AG=2a,∵=,∴OG=3a,AO=5a,
∵四边形ABCD为平行四边形,∴AO=CO=5a,AC=10a,CG=8a,
∵AD∥BC,∴△AGE∽△CGB,∴==,
∵AE=4,∴BC=16.(12分)
