第二十七章 相似 能力提优卷 (含答案)人教版九年级数学下册
文档属性
| 名称 | 第二十七章 相似 能力提优卷 (含答案)人教版九年级数学下册 |  | |
| 格式 | docx | ||
| 文件大小 | 242.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-03-30 07:58:03 | ||
图片预览



文档简介
第二十七章 相似
时间:60分钟 满分:100分
一、选择题(本题共8小题,每小题4分,共32分)
1.下列各组中的四条线段成比例的是 ( )
A.3 cm、6 cm、8 cm、9 cm B.3 cm、5 cm、6 cm、9 cm
C.3 cm、6 cm、7 cm、9 cm D.3 cm、9 cm、10 cm、30 cm
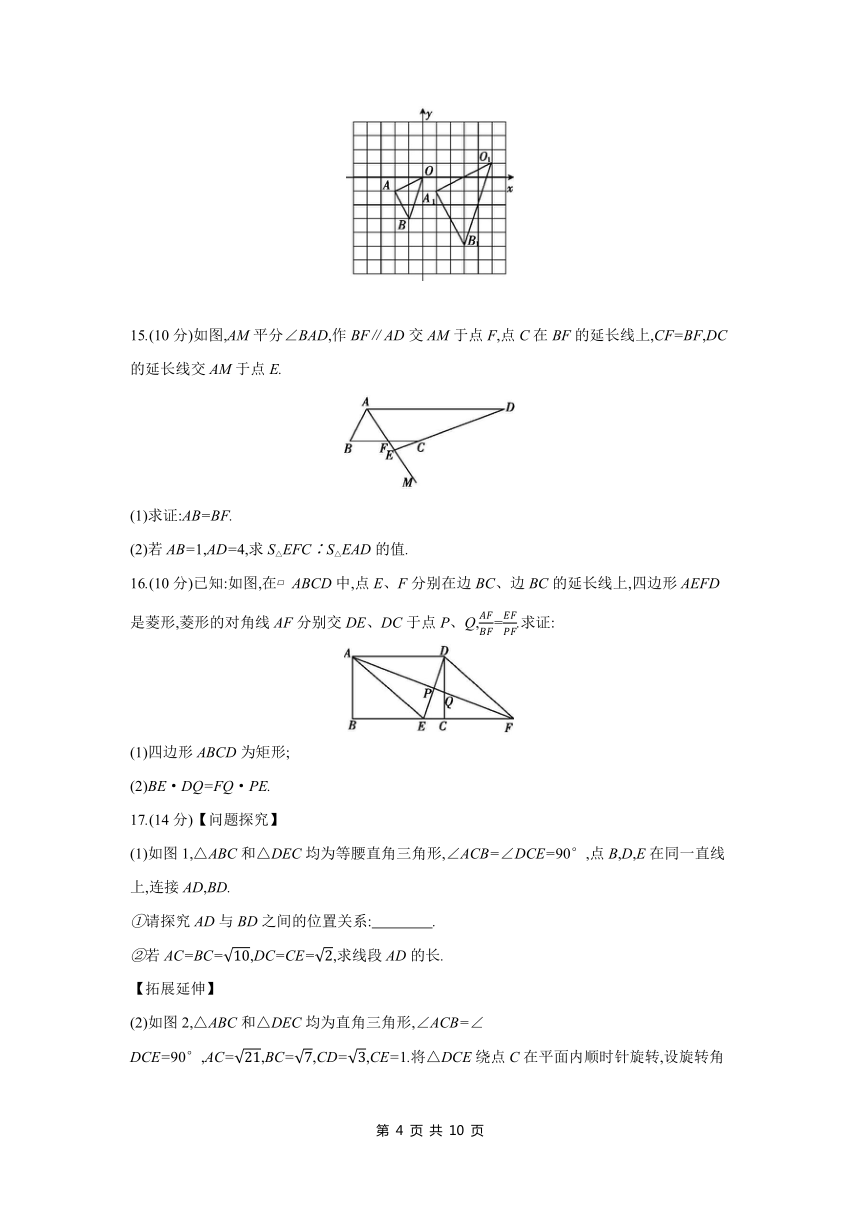
2.如图,在平面直角坐标系中,矩形OEFG与矩形ABCD是位似图形,其中对应点C和F的坐标分别为(-4,4),(2,1),则位似中心的坐标是 ( )
A.(0,2) B.(0,2.5) C.(0,3) D.(0,4)
3.如图,在△ABC中,点P在边AB上,则在下列四个条件中:①∠ACP=∠B;②∠APC=∠ACB;③AC2=AP·AB;④AB·CP=AP·CB.不能判定△APC与△ACB相似的是 ( )
A.① B.② C.③ D.④
4.如图,已知点D、E分别在△ABC的边AB、AC上,DE∥BC,点F在CD的延长线上,AF∥BC,则下列结论错误的是 ( )
A.= B.= C.= D.=
5.如图,在△ABC中,P是AB边上一点,在AC边上求作一点Q,使得△AQP∽△ABC.
甲的作法:过点P作PQ∥BC,交AC于点Q,则点Q即为所求.
乙的作法:经过点P,B,C作☉O,交AC于点Q,则点Q即为所求.
对于甲、乙的作法,下列判断正确的是 ( )
A.甲错误,乙正确 B.甲正确,乙错误
C.甲、乙都错误 D.甲、乙都正确
6.如图,这是一块矩形场地ABCD,宽AB=8米,长BC=12米.若在其对角线AC,BD所在的直线上取点E,F,G,H,扩建为新的矩形场地,左、右各增加了0.6米,上、下各增加了x米,则x的值为 ( )
A.0.2 B.0.3 C.0.4 D.0.5
7.一个直角三角形木架的两条直角边的边长分别是30 cm,40 cm.现要做一个与其相似的三角形木架,如果以60 cm长的木条为其中一边,那么另两边中长度最大的一边最多可达到 ( )
A.60 cm B.75 cm C.100 cm D.120 cm
8.如图,在矩形ABCD中,AB=6,BC=3,E是对角线BD上一动点,过点E作MN⊥BD,交AB于点M,交CD于点N,当点E在BD上移动时,MN的长是 ( )
A.3 B. C. D.无法确定
二、填空题(本题共4小题,每小题4分,共16分)
9.如图,为了确定一条河的宽度,测量人员观察到在对岸岸边P点处有一根柱子,再在他们所在的这一侧岸上选点A和点B,使得B,A,P在同一条直线上,且与河岸垂直,随后确定点C,点D,使AC⊥BP,BD⊥BP,由观测可以确定AC与DP的交点C.他们测得AB=20 m,AC=40 m,BD=50 m,从而确定河宽PA为 m.
10.如图,在△ABC中,D、E为边AB的三等分点,EF∥DG∥AC,H为AF与DG的交点.若AC=6,则DH= .
11.如图,有一正方形ABCD,边长为4,点E是边CD上的中点,对角线BD上有一动点F,当顶点为A、B、F的三角形与顶点为D、E、F的三角形相似时,BF的值为 .
12.如图,在平面直角坐标系中,正方形A1B1C1A2与正方形A2B2C2A3是以点O为位似中心的位似图形,且位似比为,点A1,A2,A3在x轴上,延长A3C2交射线OB1于点B3,以A3B3为边作正方形A3B3C3A4;延长A4C3交射线OB1于点B4,以A4B4为边作正方形A4B4C4A5;….按照这样的规律继续作下去,若OA1=1,则正方形A2022B2022C2022A2023的面积为 .
三、解答题(本大题共5小题,共52分)
13.(8分)已知==.
(1)求的值;(2)若2x+3y-z=17,求x+2y-z的值.
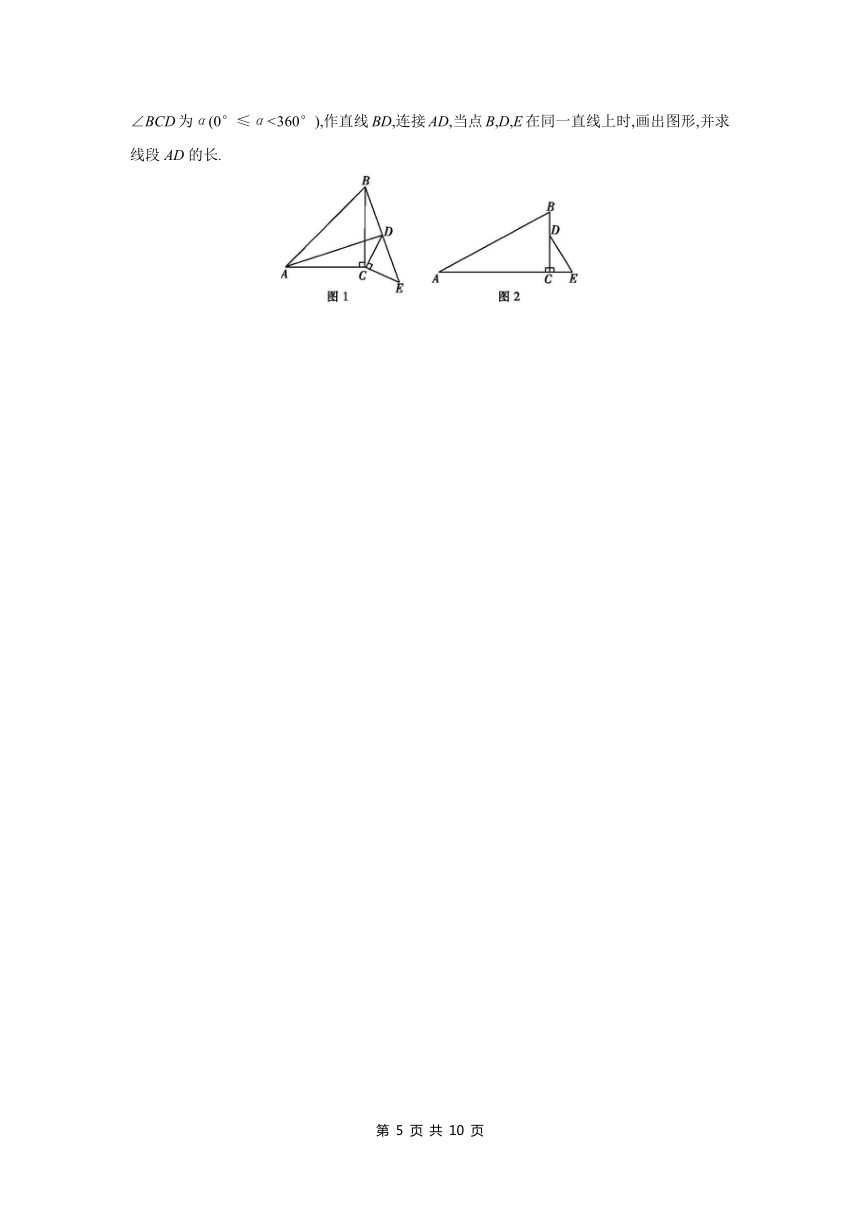
14.(10分)在如图所示的方格纸中,△OAB的顶点坐标分别为O(0,0),A(-2,-1),B(-1,-3),△O1A1B1与△OAB是关于点P为位似中心的位似图形.
(1)在图中标出位似中心点P的位置,并写出点P及点B的对应点B1的坐标;
(2)以原点O为位似中心,在位似中心的同侧画出△OAB的一个位似△OA2B2,使它与△OAB的位似比为2∶1,并写出点B的对应点B2的坐标.
15.(10分)如图,AM平分∠BAD,作BF∥AD交AM于点F,点C在BF的延长线上,CF=BF,DC的延长线交AM于点E.
(1)求证:AB=BF.
(2)若AB=1,AD=4,求S△EFC∶S△EAD的值.
16.(10分)已知:如图,在 ABCD中,点E、F分别在边BC、边BC的延长线上,四边形AEFD是菱形,菱形的对角线AF分别交DE、DC于点P、Q,=.求证:
(1)四边形ABCD为矩形;
(2)BE·DQ=FQ·PE.
17.(14分)【问题探究】
(1)如图1,△ABC和△DEC均为等腰直角三角形,∠ACB=∠DCE=90°,点B,D,E在同一直线上,连接AD,BD.
①请探究AD与BD之间的位置关系: .
②若AC=BC=,DC=CE=,求线段AD的长.
【拓展延伸】
(2)如图2,△ABC和△DEC均为直角三角形,∠ACB=∠DCE=90°,AC=,BC=,CD=,CE=1.将△DCE绕点C在平面内顺时针旋转,设旋转角∠BCD为α(0°≤α<360°),作直线BD,连接AD,当点B,D,E在同一直线上时,画出图形,并求线段AD的长.
参考答案
一、选择题
1 2 3 4 5 6 7 8
D A D D A C C C
1.D 【解析】A.∵3×9≠6×8,∴四条线段不成比例;B.∵3×9≠5×6,∴四条线段不成比例;C.∵3×9≠6×7,∴四条线段不成比例;D.∵3×30=9×10,∴四条线段成比例.
2.A 【解析】如图,连接CF,交y轴于点P,则点P为位似中心,由题意得CD=4,GF=2,DG=3,OG=1,∵CD∥GF,∴△CDP∽△FGP,∴=,即=,解得GP=1,∴OP=2,∴位似中心点P的坐标为(0,2).
3.D 【解析】①当∠ACP=∠B时,∵∠A=∠A,∴△APC∽△ACB,∴①不符合题意;②当∠APC=∠ACB时,∵∠A=∠A,∴△APC∽△ACB,∴②不符合题意;③当AC2=AP·AB时,即AC∶AB=AP∶AC,∵∠A=∠A,∴△APC∽△ACB,∴③不符合题意;④∵当AB·CP=AP·CB,即PC∶BC=AP∶AB,而∠APC≠∠ABC,∴不能判断△APC和△ACB相似,∴④符合题意.
4.D 【解析】∵DE∥BC,∴=,∵DE∥BC,AF∥BC,∴DE∥AF,∴∠DEC=∠FAC,∵∠DCE=∠FCA,∴△FAC∽△DEC,∴=,∴=,故A正确;∵DE∥AF,∴=,即=,故B正确;∵DE∥BC,∴=,故C正确;∵AF∥BC,∴∠FAD=∠CBD,∵∠ADF=∠BDC,∴△ADF∽△BDC,∴=,∵△FAC∽△DEC,∴=.∵与不一定相等,故D错误.
5.A 【解析】乙的作法正确.理由:∵B,C,Q,P四点共圆,∴∠B+∠CQP=180°,∵∠AQP+∠CQP=180°,∴∠AQP=∠B,∵∠A=∠A,∴△AQP∽△ABC.甲的作法,无法证明∠AQP=∠B,故甲的作法错误.
6.C 【解析】由题意得,AD∥EH,AB∥EF,∴△AOD∽△EOH,△AOB∽△EOF,∴=,=,∴=,∵左、右各增加了0.6米,上、下各增加了x米,AB=8米,BC=12米.∴EH=12+2×0.6=13.2,EF=8+2x,∴=,解得x=0.4.
7.C 【解析】∵一个直角三角形木架的两条直角边的边长分别是30 cm,40 cm,∴三角形的斜边长为=50(cm),∵现要做一个与其相似的三角形木架,以60 cm长的木条为其中一边,∴当另两边中长度最大的一边最长,则两三角形的相似比为30∶60=1∶2,故设要做的三角形最长边长为50×2=100(cm).
8.C 【解析】如图,过点M作MH⊥DC于点H,∴∠MHC=∠C=∠ABC=90°,∴四边形BCHM是矩形,∴MH=BC=3,∵AB=CD=6,BC=AD=3,∴BD===3,∵MN⊥BD,∴∠DEN=∠MHN=∠C=90°,∴∠MNH+∠BDC=∠BDC+∠DBC=90°,∴∠DBC=∠MNH,∴△DBC∽△MNH,∴=,∴=,∴MN=.
二、填空题
9 10 11 12
80 1 2或 24042
9.80 【解析】∵AC⊥BP,BD⊥BP,∴AC∥BD,∴△PBD∽△PAC,∴=,∵AB=20 m,AC=40 m,BD=50 m,即=,解得PA=80 m.
10.1 【解析】∵D、E为边AB的三等分点,EF∥DG∥AC,∴BE=DE=AD,BF=GF=CG,AH=HF,∴AB=3BE,DH是△AEF的中位线,∴DH=EF,∵EF∥AC,∴△BEF∽△BAC,∴=,即=,解得EF=2,∴DH=EF=×2=1.
11.2或 【解析】依题意可得BD===4,设BF=x,则有DF=4-x.①当△ABF∽△FDE时,如图1,由=,得=,解得x1=x2=2;②当△ABF∽△EDF时,如图2,由=,得=,解得x=.综上所述,BF的值为2或.
图1 图2
12.24042 【解析】∵正方形A1B1C1A2与正方形A2B2C2A3是以原点O为位似中心的位似图形,且相似比为,∴=,∵A1B1⊥x轴,A2B2⊥x轴,∴A1B1∥A2B2,∴△OA1B1∽△OA2B2,∴==,∵OA1=1,∴OA2=2,∴A1A2=1,∴正方形A1B1C1A2的面积=1=40,∵OA1=A1A2=A1B1=1,∴∠B1OA1=45°,∴OA2=A2B2=2,∴正方形A2B2C2A3的面积=2×2=41,∵A3B3⊥x轴,OA3=A3B3=4,∴正方形A3B3C3A4的面积=4×4=16=42,…,则正方形A2022B2022C2022A2023的面积为42022-1=24042.
三、解答题
13.解:设===k(k≠0),则x=3k,y=5k,z=4k.
(1)==-.(4分)
(2)∵2x+3y-z=17,
∴6k+15k-4k=17,∴k=1,
∴x+2y-z=3k+10k-4k=9k=9×1=9.(8分)
14.解:(1)如图,P(-5,-1),B1(3,-5).(4分)
(2)如图,△OA2B2即为所求作.B2(-2,-6).(10分)
15.解:(1)证明:∵AM平分∠BAD,
∴∠BAM=∠DAM,
∵BF∥AD,∴∠BFA=∠DAM,∴∠BAM=∠BFA,
∴AB=BF.(4分)
(2)∵AB=1,∴AB=BF=CF=1,
∵BF∥AD,∴△CEF∽△DEA,∴==.(10分)
16.证明:(1)∵四边形ADFE是菱形,∴AF⊥DE,
∴∠EPF=90°,
∵=,∠PFE=∠AFB,∴△ABF∽△EPF,
∴∠ABE=∠EPF=90°,
∴平行四边形ABCD是矩形;(5分)
(2)∵四边形ABCD是矩形,
∴AD=BC=EF,∴EC+CF=BE+CE,∴BE=CF,
∵四边形AEFD是菱形,∴DP=EP,
∵∠DPF=∠QCF=90°,∠CQF=∠PQD,∴△DPQ∽△FCQ,
∴=,∴=,∴BE·DQ=FQ·PE.(10分)
17.解:【问题探究】
(1)①∵△ABC和△DEC均为等腰直角三角形,
∴AC=BC,CE=CD,∠ABC=∠DEC=45°=∠CDE,
∵∠ACB=∠DCE=90°,∴∠ACD=∠BCE,且AC=BC,CE=CD,
∴△ACD≌△BCE(SAS),∴∠ADC=∠BEC=45°,
∴∠ADE=∠ADC+∠CDE=90°,∴AD⊥BD.故答案为AD⊥BD.(3分)
②如图,过点C作CF⊥AD于点F,
∵∠ADC=45°,CF⊥AD,CD=,∴DF=CF=1,
∴AF==3,∴AD=AF+DF=4.(8分)
【拓展延伸】
(2)①若点D在BC右侧,如图,过点C作CF⊥AD于点F,
∵∠ACB=∠DCE=90°,AC=,BC=,CD=,CE=1.
∴∠ACD=∠BCE,==,
∴△ACD∽△BCE,∴∠ADC=∠BEC,
∵CD=,CE=1,∴DE==2,
∵∠ADC=∠BEC,∠DCE=∠CFD=90°,
∴△DCE∽△CFD,
∴==,即==,
∴CF=,DF=,∴AF==,∴AD=DF+AF=3.
②若点D在BC左侧,如图,过点C作CF⊥AD交AD的延长线于点F,
与①类似得CF=,DF=,AF=,
∴AD=AF-DF=2.
综上所述,AD的长为2或3.(14分)
时间:60分钟 满分:100分
一、选择题(本题共8小题,每小题4分,共32分)
1.下列各组中的四条线段成比例的是 ( )
A.3 cm、6 cm、8 cm、9 cm B.3 cm、5 cm、6 cm、9 cm
C.3 cm、6 cm、7 cm、9 cm D.3 cm、9 cm、10 cm、30 cm
2.如图,在平面直角坐标系中,矩形OEFG与矩形ABCD是位似图形,其中对应点C和F的坐标分别为(-4,4),(2,1),则位似中心的坐标是 ( )
A.(0,2) B.(0,2.5) C.(0,3) D.(0,4)
3.如图,在△ABC中,点P在边AB上,则在下列四个条件中:①∠ACP=∠B;②∠APC=∠ACB;③AC2=AP·AB;④AB·CP=AP·CB.不能判定△APC与△ACB相似的是 ( )
A.① B.② C.③ D.④
4.如图,已知点D、E分别在△ABC的边AB、AC上,DE∥BC,点F在CD的延长线上,AF∥BC,则下列结论错误的是 ( )
A.= B.= C.= D.=
5.如图,在△ABC中,P是AB边上一点,在AC边上求作一点Q,使得△AQP∽△ABC.
甲的作法:过点P作PQ∥BC,交AC于点Q,则点Q即为所求.
乙的作法:经过点P,B,C作☉O,交AC于点Q,则点Q即为所求.
对于甲、乙的作法,下列判断正确的是 ( )
A.甲错误,乙正确 B.甲正确,乙错误
C.甲、乙都错误 D.甲、乙都正确
6.如图,这是一块矩形场地ABCD,宽AB=8米,长BC=12米.若在其对角线AC,BD所在的直线上取点E,F,G,H,扩建为新的矩形场地,左、右各增加了0.6米,上、下各增加了x米,则x的值为 ( )
A.0.2 B.0.3 C.0.4 D.0.5
7.一个直角三角形木架的两条直角边的边长分别是30 cm,40 cm.现要做一个与其相似的三角形木架,如果以60 cm长的木条为其中一边,那么另两边中长度最大的一边最多可达到 ( )
A.60 cm B.75 cm C.100 cm D.120 cm
8.如图,在矩形ABCD中,AB=6,BC=3,E是对角线BD上一动点,过点E作MN⊥BD,交AB于点M,交CD于点N,当点E在BD上移动时,MN的长是 ( )
A.3 B. C. D.无法确定
二、填空题(本题共4小题,每小题4分,共16分)
9.如图,为了确定一条河的宽度,测量人员观察到在对岸岸边P点处有一根柱子,再在他们所在的这一侧岸上选点A和点B,使得B,A,P在同一条直线上,且与河岸垂直,随后确定点C,点D,使AC⊥BP,BD⊥BP,由观测可以确定AC与DP的交点C.他们测得AB=20 m,AC=40 m,BD=50 m,从而确定河宽PA为 m.
10.如图,在△ABC中,D、E为边AB的三等分点,EF∥DG∥AC,H为AF与DG的交点.若AC=6,则DH= .
11.如图,有一正方形ABCD,边长为4,点E是边CD上的中点,对角线BD上有一动点F,当顶点为A、B、F的三角形与顶点为D、E、F的三角形相似时,BF的值为 .
12.如图,在平面直角坐标系中,正方形A1B1C1A2与正方形A2B2C2A3是以点O为位似中心的位似图形,且位似比为,点A1,A2,A3在x轴上,延长A3C2交射线OB1于点B3,以A3B3为边作正方形A3B3C3A4;延长A4C3交射线OB1于点B4,以A4B4为边作正方形A4B4C4A5;….按照这样的规律继续作下去,若OA1=1,则正方形A2022B2022C2022A2023的面积为 .
三、解答题(本大题共5小题,共52分)
13.(8分)已知==.
(1)求的值;(2)若2x+3y-z=17,求x+2y-z的值.
14.(10分)在如图所示的方格纸中,△OAB的顶点坐标分别为O(0,0),A(-2,-1),B(-1,-3),△O1A1B1与△OAB是关于点P为位似中心的位似图形.
(1)在图中标出位似中心点P的位置,并写出点P及点B的对应点B1的坐标;
(2)以原点O为位似中心,在位似中心的同侧画出△OAB的一个位似△OA2B2,使它与△OAB的位似比为2∶1,并写出点B的对应点B2的坐标.
15.(10分)如图,AM平分∠BAD,作BF∥AD交AM于点F,点C在BF的延长线上,CF=BF,DC的延长线交AM于点E.
(1)求证:AB=BF.
(2)若AB=1,AD=4,求S△EFC∶S△EAD的值.
16.(10分)已知:如图,在 ABCD中,点E、F分别在边BC、边BC的延长线上,四边形AEFD是菱形,菱形的对角线AF分别交DE、DC于点P、Q,=.求证:
(1)四边形ABCD为矩形;
(2)BE·DQ=FQ·PE.
17.(14分)【问题探究】
(1)如图1,△ABC和△DEC均为等腰直角三角形,∠ACB=∠DCE=90°,点B,D,E在同一直线上,连接AD,BD.
①请探究AD与BD之间的位置关系: .
②若AC=BC=,DC=CE=,求线段AD的长.
【拓展延伸】
(2)如图2,△ABC和△DEC均为直角三角形,∠ACB=∠DCE=90°,AC=,BC=,CD=,CE=1.将△DCE绕点C在平面内顺时针旋转,设旋转角∠BCD为α(0°≤α<360°),作直线BD,连接AD,当点B,D,E在同一直线上时,画出图形,并求线段AD的长.
参考答案
一、选择题
1 2 3 4 5 6 7 8
D A D D A C C C
1.D 【解析】A.∵3×9≠6×8,∴四条线段不成比例;B.∵3×9≠5×6,∴四条线段不成比例;C.∵3×9≠6×7,∴四条线段不成比例;D.∵3×30=9×10,∴四条线段成比例.
2.A 【解析】如图,连接CF,交y轴于点P,则点P为位似中心,由题意得CD=4,GF=2,DG=3,OG=1,∵CD∥GF,∴△CDP∽△FGP,∴=,即=,解得GP=1,∴OP=2,∴位似中心点P的坐标为(0,2).
3.D 【解析】①当∠ACP=∠B时,∵∠A=∠A,∴△APC∽△ACB,∴①不符合题意;②当∠APC=∠ACB时,∵∠A=∠A,∴△APC∽△ACB,∴②不符合题意;③当AC2=AP·AB时,即AC∶AB=AP∶AC,∵∠A=∠A,∴△APC∽△ACB,∴③不符合题意;④∵当AB·CP=AP·CB,即PC∶BC=AP∶AB,而∠APC≠∠ABC,∴不能判断△APC和△ACB相似,∴④符合题意.
4.D 【解析】∵DE∥BC,∴=,∵DE∥BC,AF∥BC,∴DE∥AF,∴∠DEC=∠FAC,∵∠DCE=∠FCA,∴△FAC∽△DEC,∴=,∴=,故A正确;∵DE∥AF,∴=,即=,故B正确;∵DE∥BC,∴=,故C正确;∵AF∥BC,∴∠FAD=∠CBD,∵∠ADF=∠BDC,∴△ADF∽△BDC,∴=,∵△FAC∽△DEC,∴=.∵与不一定相等,故D错误.
5.A 【解析】乙的作法正确.理由:∵B,C,Q,P四点共圆,∴∠B+∠CQP=180°,∵∠AQP+∠CQP=180°,∴∠AQP=∠B,∵∠A=∠A,∴△AQP∽△ABC.甲的作法,无法证明∠AQP=∠B,故甲的作法错误.
6.C 【解析】由题意得,AD∥EH,AB∥EF,∴△AOD∽△EOH,△AOB∽△EOF,∴=,=,∴=,∵左、右各增加了0.6米,上、下各增加了x米,AB=8米,BC=12米.∴EH=12+2×0.6=13.2,EF=8+2x,∴=,解得x=0.4.
7.C 【解析】∵一个直角三角形木架的两条直角边的边长分别是30 cm,40 cm,∴三角形的斜边长为=50(cm),∵现要做一个与其相似的三角形木架,以60 cm长的木条为其中一边,∴当另两边中长度最大的一边最长,则两三角形的相似比为30∶60=1∶2,故设要做的三角形最长边长为50×2=100(cm).
8.C 【解析】如图,过点M作MH⊥DC于点H,∴∠MHC=∠C=∠ABC=90°,∴四边形BCHM是矩形,∴MH=BC=3,∵AB=CD=6,BC=AD=3,∴BD===3,∵MN⊥BD,∴∠DEN=∠MHN=∠C=90°,∴∠MNH+∠BDC=∠BDC+∠DBC=90°,∴∠DBC=∠MNH,∴△DBC∽△MNH,∴=,∴=,∴MN=.
二、填空题
9 10 11 12
80 1 2或 24042
9.80 【解析】∵AC⊥BP,BD⊥BP,∴AC∥BD,∴△PBD∽△PAC,∴=,∵AB=20 m,AC=40 m,BD=50 m,即=,解得PA=80 m.
10.1 【解析】∵D、E为边AB的三等分点,EF∥DG∥AC,∴BE=DE=AD,BF=GF=CG,AH=HF,∴AB=3BE,DH是△AEF的中位线,∴DH=EF,∵EF∥AC,∴△BEF∽△BAC,∴=,即=,解得EF=2,∴DH=EF=×2=1.
11.2或 【解析】依题意可得BD===4,设BF=x,则有DF=4-x.①当△ABF∽△FDE时,如图1,由=,得=,解得x1=x2=2;②当△ABF∽△EDF时,如图2,由=,得=,解得x=.综上所述,BF的值为2或.
图1 图2
12.24042 【解析】∵正方形A1B1C1A2与正方形A2B2C2A3是以原点O为位似中心的位似图形,且相似比为,∴=,∵A1B1⊥x轴,A2B2⊥x轴,∴A1B1∥A2B2,∴△OA1B1∽△OA2B2,∴==,∵OA1=1,∴OA2=2,∴A1A2=1,∴正方形A1B1C1A2的面积=1=40,∵OA1=A1A2=A1B1=1,∴∠B1OA1=45°,∴OA2=A2B2=2,∴正方形A2B2C2A3的面积=2×2=41,∵A3B3⊥x轴,OA3=A3B3=4,∴正方形A3B3C3A4的面积=4×4=16=42,…,则正方形A2022B2022C2022A2023的面积为42022-1=24042.
三、解答题
13.解:设===k(k≠0),则x=3k,y=5k,z=4k.
(1)==-.(4分)
(2)∵2x+3y-z=17,
∴6k+15k-4k=17,∴k=1,
∴x+2y-z=3k+10k-4k=9k=9×1=9.(8分)
14.解:(1)如图,P(-5,-1),B1(3,-5).(4分)
(2)如图,△OA2B2即为所求作.B2(-2,-6).(10分)
15.解:(1)证明:∵AM平分∠BAD,
∴∠BAM=∠DAM,
∵BF∥AD,∴∠BFA=∠DAM,∴∠BAM=∠BFA,
∴AB=BF.(4分)
(2)∵AB=1,∴AB=BF=CF=1,
∵BF∥AD,∴△CEF∽△DEA,∴==.(10分)
16.证明:(1)∵四边形ADFE是菱形,∴AF⊥DE,
∴∠EPF=90°,
∵=,∠PFE=∠AFB,∴△ABF∽△EPF,
∴∠ABE=∠EPF=90°,
∴平行四边形ABCD是矩形;(5分)
(2)∵四边形ABCD是矩形,
∴AD=BC=EF,∴EC+CF=BE+CE,∴BE=CF,
∵四边形AEFD是菱形,∴DP=EP,
∵∠DPF=∠QCF=90°,∠CQF=∠PQD,∴△DPQ∽△FCQ,
∴=,∴=,∴BE·DQ=FQ·PE.(10分)
17.解:【问题探究】
(1)①∵△ABC和△DEC均为等腰直角三角形,
∴AC=BC,CE=CD,∠ABC=∠DEC=45°=∠CDE,
∵∠ACB=∠DCE=90°,∴∠ACD=∠BCE,且AC=BC,CE=CD,
∴△ACD≌△BCE(SAS),∴∠ADC=∠BEC=45°,
∴∠ADE=∠ADC+∠CDE=90°,∴AD⊥BD.故答案为AD⊥BD.(3分)
②如图,过点C作CF⊥AD于点F,
∵∠ADC=45°,CF⊥AD,CD=,∴DF=CF=1,
∴AF==3,∴AD=AF+DF=4.(8分)
【拓展延伸】
(2)①若点D在BC右侧,如图,过点C作CF⊥AD于点F,
∵∠ACB=∠DCE=90°,AC=,BC=,CD=,CE=1.
∴∠ACD=∠BCE,==,
∴△ACD∽△BCE,∴∠ADC=∠BEC,
∵CD=,CE=1,∴DE==2,
∵∠ADC=∠BEC,∠DCE=∠CFD=90°,
∴△DCE∽△CFD,
∴==,即==,
∴CF=,DF=,∴AF==,∴AD=DF+AF=3.
②若点D在BC左侧,如图,过点C作CF⊥AD交AD的延长线于点F,
与①类似得CF=,DF=,AF=,
∴AD=AF-DF=2.
综上所述,AD的长为2或3.(14分)
