第二十三章 旋转 基础闯关卷(含答案) 人教版九年级数学上册
文档属性
| 名称 | 第二十三章 旋转 基础闯关卷(含答案) 人教版九年级数学上册 |  | |
| 格式 | docx | ||
| 文件大小 | 230.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-03-30 07:58:16 | ||
图片预览


文档简介
第二十三章 旋转
时间:60分钟 满分:100分
一、选择题(本题共8小题,每小题4分,共32分)
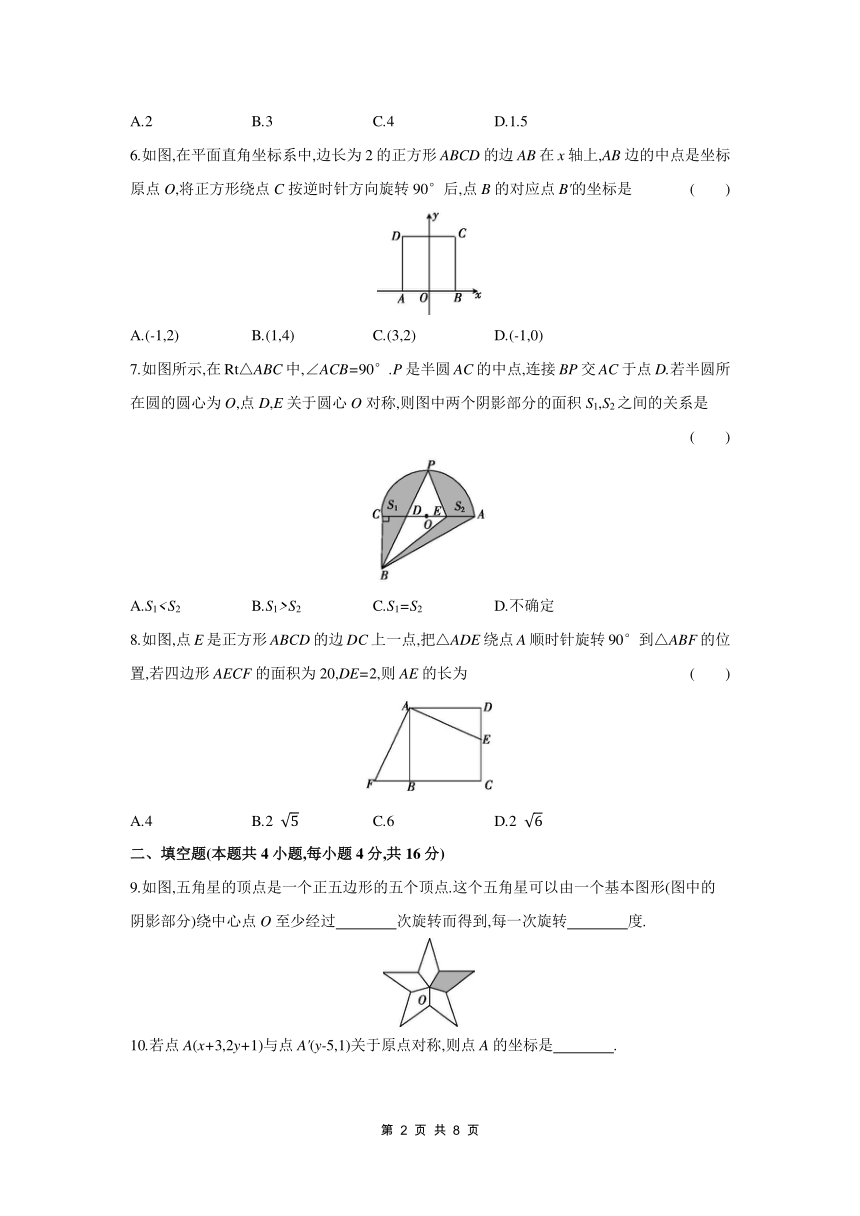
1.下列图形中,不是中心对称图形的是 ( )
2.如图所示,将△AOB绕点O按逆时针方向旋转45°后得到△A'OB',若∠AOB'=30°,那么∠AOB的度数是 ( )
A.15° B.30° C.45° D.60°
3.如果要将图中的甲图案变成乙图案,可经过的变换正确的是 ( )
A.轴对称、平移 B.平移、轴对称 C.旋转、轴对称 D.平移、旋转
4.如图所示,在4×4的正方形网格中,△MNP绕某点旋转一定的角度,得到△M1N1P1,则其旋转中心是 ( )
A.点A B.点B C.点C D.点D
如图,将△ABC以点O为旋转中心旋转180°后得到△A'B'C'.ED是△ABC的中位线,经旋转后变为线段E'D'.已知BC=4,则线段E'D'的长度为 ( )
A.2 B.3 C.4 D.1.5
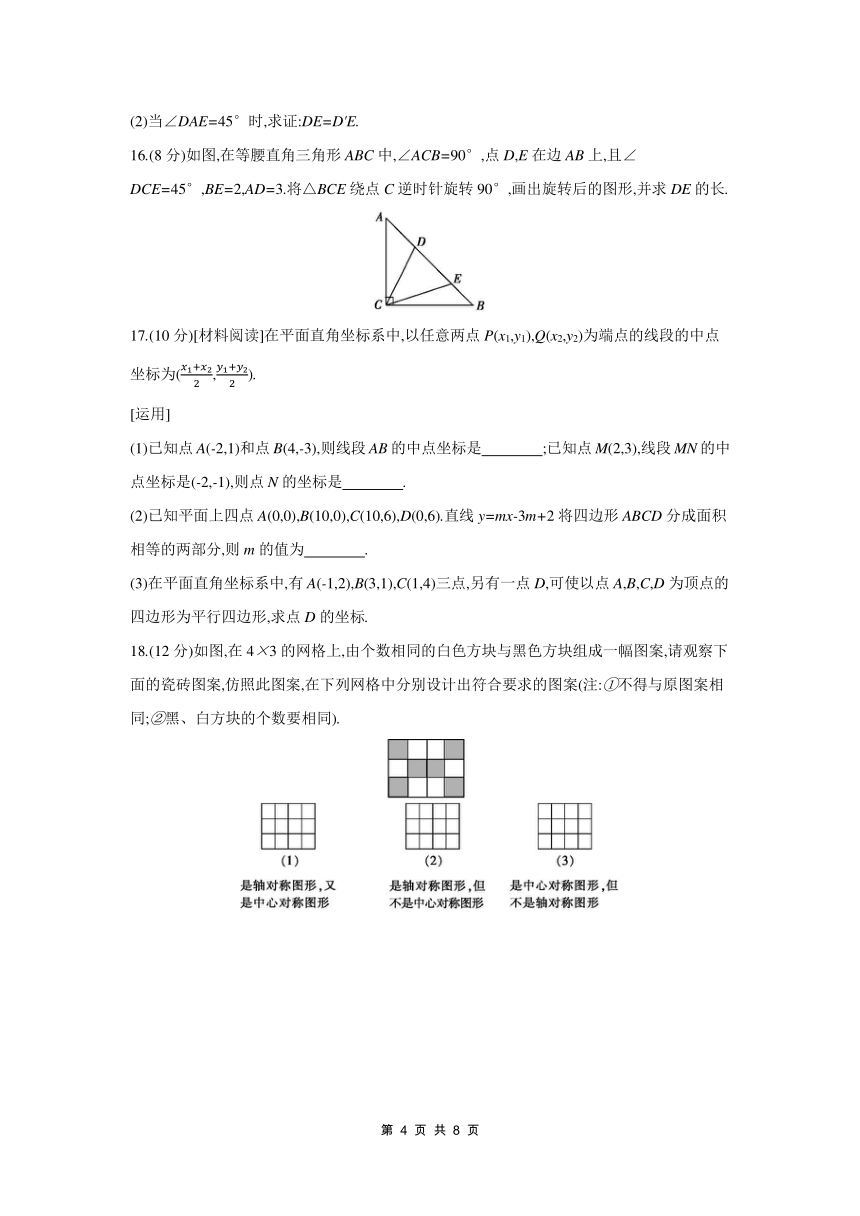
6.如图,在平面直角坐标系中,边长为2的正方形ABCD的边AB在x轴上,AB边的中点是坐标原点O,将正方形绕点C按逆时针方向旋转90°后,点B的对应点B'的坐标是 ( )
A.(-1,2) B.(1,4) C.(3,2) D.(-1,0)
7.如图所示,在Rt△ABC中,∠ACB=90°.P是半圆AC的中点,连接BP交AC于点D.若半圆所在圆的圆心为O,点D,E关于圆心O对称,则图中两个阴影部分的面积S1,S2之间的关系是 ( )
A.S1S2 C.S1=S2 D.不确定
8.如图,点E是正方形ABCD的边DC上一点,把△ADE绕点A顺时针旋转90°到△ABF的位置,若四边形AECF的面积为20,DE=2,则AE的长为 ( )
A.4 B.2 C.6 D.2
二、填空题(本题共4小题,每小题4分,共16分)
9.如图,五角星的顶点是一个正五边形的五个顶点.这个五角星可以由一个基本图形(图中的阴影部分)绕中心点O至少经过 次旋转而得到,每一次旋转 度.
10.若点A(x+3,2y+1)与点A'(y-5,1)关于原点对称,则点A的坐标是 .
11.如图,将△ABC绕点C(0,1)旋转180°得到△A'B'C,设点A的坐标为(a,b),则点A'的坐标为 .
12.一副三角尺按如图所示的方式放置,将三角尺ADE绕点A逆时针旋转α(0°<α<90°),使得三角尺ADE的一边所在的直线与BC垂直,则α的度数为 .
三、解答题(本大题共6小题,共52分)
13.(6分)如图,△ABO与△CDO关于点O中心对称,点E,F在线段AC上,且AF=CE.求证:DF=BE.
14.(8分)如图,将一个钝角三角形ABC(其中∠ABC=120°)绕点B顺时针旋转得到△A1BC1,使得点C落在AB的延长线上的点C1处,连接AA1.
(1)写出旋转角的度数;
(2)求证:∠A1AC=∠C1.
15.(8分)如图,在△ABC中,∠BAC=90°,AB=AC,D,E是BC边上的点,将△ABD绕点A逆时针旋转得到△ACD'.
(1)求∠DAD'的度数.
(2)当∠DAE=45°时,求证:DE=D'E.
16.(8分)如图,在等腰直角三角形ABC中,∠ACB=90°,点D,E在边AB上,且∠DCE=45°,BE=2,AD=3.将△BCE绕点C逆时针旋转90°,画出旋转后的图形,并求DE的长.
17.(10分)[材料阅读]在平面直角坐标系中,以任意两点P(x1,y1),Q(x2,y2)为端点的线段的中点坐标为(,).
[运用]
(1)已知点A(-2,1)和点B(4,-3),则线段AB的中点坐标是 ;已知点M(2,3),线段MN的中点坐标是(-2,-1),则点N的坐标是 .
(2)已知平面上四点A(0,0),B(10,0),C(10,6),D(0,6).直线y=mx-3m+2将四边形ABCD分成面积相等的两部分,则m的值为 .
(3)在平面直角坐标系中,有A(-1,2),B(3,1),C(1,4)三点,另有一点D,可使以点A,B,C,D为顶点的四边形为平行四边形,求点D的坐标.
18.(12分)如图,在4×3的网格上,由个数相同的白色方块与黑色方块组成一幅图案,请观察下面的瓷砖图案,仿照此图案,在下列网格中分别设计出符合要求的图案(注:①不得与原图案相同;②黑、白方块的个数要相同).
参考答案
一、选择题
1 2 3 4 5 6 7 8
C A D B A C C D
2.A 【解析】∵将△AOB绕点O按逆时针方向旋转45°后得到△A'OB',∴∠A'OA=45°,∠AOB=∠A'OB',∴∠AOB=∠A'OB'=∠A'OA-∠AOB'=45°-30°=15°.
4.B 【解析】旋转中心到对应点的距离相等.
5.A 【解析】∵ED是△ABC的中位线,BC=4,∴ED=2.又∵△A'B'C'和△ABC关于点O中心对称,∴E'D'=ED=2.
7.C 【解析】∵P是半圆AC的中点,∴半圆关于直线OP对称,且点D,E关于圆心O对称,因而S1,S2在直径AC上面的部分面积相等.∵OD=OE,∴CD=AE.∵△CDB的底边CD与△AEB的底边AE相等,高相同,∴它们的面积相等,∴S1=S2.
8.D 【解析】由旋转可得,S正方形ABCD=S四边形AECF=20,即AD2=20,∴AD=2 .∵DE=2,∴在Rt△ADE中,AE==2 .
二、填空题
9 10 11 12
4 72 (6,-1) (-a,-b+2) 15°或60°
10.(6,-1) 【解析】依题意,得,解得,∴点A的坐标为(6,-1).
11.(-a,-b+2) 【解析】如图,过点A作AD⊥y轴于点D,过点A'作A'D'⊥y轴于点D',则△ACD≌△A'CD',∴A'D'=AD=a,CD'=CD=-b+1,∴OD'=-b+2,∴点A'的坐标为(-a,-b+2).
12.15°或60° 【解析】分情况讨论:①若DE⊥BC,设此时直线AD与BC交于点F,则∠BFA=90°-45°=45°,∴∠BAD=180°-60°-45°=75°,∴α=90°-∠BAD=15°;②若AD⊥BC,则∠BAD=30°,∴α=90°-∠BAD=60°.
三、解答题
13.证明:∵△ABO与△CDO关于点O中心对称,
∴BO=DO,AO=CO.
∵AF=CE,∴AO-AF=CO-CE,即FO=EO.(2分)
在△FOD和△EOB中,
∴△FOD≌△EOB(SAS),∴DF=BE.(6分)
14.解:(1)旋转角的度数为60°.(3分)
(2)证明:由旋转的性质知∠ABC=∠A1BC1=120°,∠C=∠C1,AB=A1B.
∵点A,B,C1在同一直线上,∴∠ABC1=180°,
∴∠ABA1=∠CBC1=60°,∴∠A1BC=60°,
∵AB=A1B,∴△ABA1是等边三角形,(6分)
∴∠AA1B=∠A1BC=60°,∴AA1∥BC,∴∠A1AC=∠C.
又∵∠C=∠C1,∴∠A1AC=∠C1.(8分)
15.解:(1)∵将△ABD绕点A逆时针旋转,得到△ACD',
∴∠DAD'=∠BAC.
∵∠BAC=90°,∴∠DAD'=90°.(3分)
(2)证明:∵△ABD绕点A逆时针旋转得到△ACD',
∴AD=AD',∠DAD'=∠BAC=90°.
∵∠DAE=45°,∴∠D'AE=∠DAD'-∠DAE=90°-45°=45°,
∴∠D'AE=∠DAE.(5分)
在△AED与△AED'中,
∴△AED≌△AED'(SAS),∴DE=D'E.(8分)
16.解:将△BCE绕点C逆时针旋转90°,得到△ACF,作图如图所示:(2分)
连接DF.由旋转的性质,得CE=CF,AF=BE=2,∠ACF=∠BCE,∠CAF=∠B=45°.
∵∠ACB=90°,∠DCE=45°,
∴∠DCF=∠ACD+∠ACF=∠ACD+∠BCE=∠ACB-∠DCE=90°-45°=45°,
∴∠DCE=∠DCF.(4分)
在△CDE和△CDF中,
∴△CDE≌△CDF(SAS),∴DE=DF.(6分)
∵∠DAF=∠BAC+∠CAF=45°+45°=90°,
∴△ADF是直角三角形,∴DF2=AD2+AF2,
∴DE2=AD2+BE2=32+22=13,∴DE=.(8分)
17.解:(1)(1,-1) (-6,-5);(2分)
(2);(4分)
(3)设点D的坐标为(x,y).
若以AB为对角线,AC,BC为邻边的四边形为平行四边形,则AB,CD的中点重合,
∴解得(6分)
若以BC为对角线,AB,AC为邻边的四边形为平行四边形,则AD,BC的中点重合,
∴解得(8分)
若以AC为对角线,AB,BC为邻边的四边形为平行四边形,则BD,AC的中点重合,
∴解得
综上可知,点D的坐标为(1,-1)或(5,3)或(-3,5).(10分)
18.解:如图(1),是轴对称图形,又是中心对称图形;
如图(2),是轴对称图形,但不是中心对称图形;
如图(3),是中心对称图形,但不是轴对称图形.
每组画对一个即可,每个图形4分.
时间:60分钟 满分:100分
一、选择题(本题共8小题,每小题4分,共32分)
1.下列图形中,不是中心对称图形的是 ( )
2.如图所示,将△AOB绕点O按逆时针方向旋转45°后得到△A'OB',若∠AOB'=30°,那么∠AOB的度数是 ( )
A.15° B.30° C.45° D.60°
3.如果要将图中的甲图案变成乙图案,可经过的变换正确的是 ( )
A.轴对称、平移 B.平移、轴对称 C.旋转、轴对称 D.平移、旋转
4.如图所示,在4×4的正方形网格中,△MNP绕某点旋转一定的角度,得到△M1N1P1,则其旋转中心是 ( )
A.点A B.点B C.点C D.点D
如图,将△ABC以点O为旋转中心旋转180°后得到△A'B'C'.ED是△ABC的中位线,经旋转后变为线段E'D'.已知BC=4,则线段E'D'的长度为 ( )
A.2 B.3 C.4 D.1.5
6.如图,在平面直角坐标系中,边长为2的正方形ABCD的边AB在x轴上,AB边的中点是坐标原点O,将正方形绕点C按逆时针方向旋转90°后,点B的对应点B'的坐标是 ( )
A.(-1,2) B.(1,4) C.(3,2) D.(-1,0)
7.如图所示,在Rt△ABC中,∠ACB=90°.P是半圆AC的中点,连接BP交AC于点D.若半圆所在圆的圆心为O,点D,E关于圆心O对称,则图中两个阴影部分的面积S1,S2之间的关系是 ( )
A.S1
8.如图,点E是正方形ABCD的边DC上一点,把△ADE绕点A顺时针旋转90°到△ABF的位置,若四边形AECF的面积为20,DE=2,则AE的长为 ( )
A.4 B.2 C.6 D.2
二、填空题(本题共4小题,每小题4分,共16分)
9.如图,五角星的顶点是一个正五边形的五个顶点.这个五角星可以由一个基本图形(图中的阴影部分)绕中心点O至少经过 次旋转而得到,每一次旋转 度.
10.若点A(x+3,2y+1)与点A'(y-5,1)关于原点对称,则点A的坐标是 .
11.如图,将△ABC绕点C(0,1)旋转180°得到△A'B'C,设点A的坐标为(a,b),则点A'的坐标为 .
12.一副三角尺按如图所示的方式放置,将三角尺ADE绕点A逆时针旋转α(0°<α<90°),使得三角尺ADE的一边所在的直线与BC垂直,则α的度数为 .
三、解答题(本大题共6小题,共52分)
13.(6分)如图,△ABO与△CDO关于点O中心对称,点E,F在线段AC上,且AF=CE.求证:DF=BE.
14.(8分)如图,将一个钝角三角形ABC(其中∠ABC=120°)绕点B顺时针旋转得到△A1BC1,使得点C落在AB的延长线上的点C1处,连接AA1.
(1)写出旋转角的度数;
(2)求证:∠A1AC=∠C1.
15.(8分)如图,在△ABC中,∠BAC=90°,AB=AC,D,E是BC边上的点,将△ABD绕点A逆时针旋转得到△ACD'.
(1)求∠DAD'的度数.
(2)当∠DAE=45°时,求证:DE=D'E.
16.(8分)如图,在等腰直角三角形ABC中,∠ACB=90°,点D,E在边AB上,且∠DCE=45°,BE=2,AD=3.将△BCE绕点C逆时针旋转90°,画出旋转后的图形,并求DE的长.
17.(10分)[材料阅读]在平面直角坐标系中,以任意两点P(x1,y1),Q(x2,y2)为端点的线段的中点坐标为(,).
[运用]
(1)已知点A(-2,1)和点B(4,-3),则线段AB的中点坐标是 ;已知点M(2,3),线段MN的中点坐标是(-2,-1),则点N的坐标是 .
(2)已知平面上四点A(0,0),B(10,0),C(10,6),D(0,6).直线y=mx-3m+2将四边形ABCD分成面积相等的两部分,则m的值为 .
(3)在平面直角坐标系中,有A(-1,2),B(3,1),C(1,4)三点,另有一点D,可使以点A,B,C,D为顶点的四边形为平行四边形,求点D的坐标.
18.(12分)如图,在4×3的网格上,由个数相同的白色方块与黑色方块组成一幅图案,请观察下面的瓷砖图案,仿照此图案,在下列网格中分别设计出符合要求的图案(注:①不得与原图案相同;②黑、白方块的个数要相同).
参考答案
一、选择题
1 2 3 4 5 6 7 8
C A D B A C C D
2.A 【解析】∵将△AOB绕点O按逆时针方向旋转45°后得到△A'OB',∴∠A'OA=45°,∠AOB=∠A'OB',∴∠AOB=∠A'OB'=∠A'OA-∠AOB'=45°-30°=15°.
4.B 【解析】旋转中心到对应点的距离相等.
5.A 【解析】∵ED是△ABC的中位线,BC=4,∴ED=2.又∵△A'B'C'和△ABC关于点O中心对称,∴E'D'=ED=2.
7.C 【解析】∵P是半圆AC的中点,∴半圆关于直线OP对称,且点D,E关于圆心O对称,因而S1,S2在直径AC上面的部分面积相等.∵OD=OE,∴CD=AE.∵△CDB的底边CD与△AEB的底边AE相等,高相同,∴它们的面积相等,∴S1=S2.
8.D 【解析】由旋转可得,S正方形ABCD=S四边形AECF=20,即AD2=20,∴AD=2 .∵DE=2,∴在Rt△ADE中,AE==2 .
二、填空题
9 10 11 12
4 72 (6,-1) (-a,-b+2) 15°或60°
10.(6,-1) 【解析】依题意,得,解得,∴点A的坐标为(6,-1).
11.(-a,-b+2) 【解析】如图,过点A作AD⊥y轴于点D,过点A'作A'D'⊥y轴于点D',则△ACD≌△A'CD',∴A'D'=AD=a,CD'=CD=-b+1,∴OD'=-b+2,∴点A'的坐标为(-a,-b+2).
12.15°或60° 【解析】分情况讨论:①若DE⊥BC,设此时直线AD与BC交于点F,则∠BFA=90°-45°=45°,∴∠BAD=180°-60°-45°=75°,∴α=90°-∠BAD=15°;②若AD⊥BC,则∠BAD=30°,∴α=90°-∠BAD=60°.
三、解答题
13.证明:∵△ABO与△CDO关于点O中心对称,
∴BO=DO,AO=CO.
∵AF=CE,∴AO-AF=CO-CE,即FO=EO.(2分)
在△FOD和△EOB中,
∴△FOD≌△EOB(SAS),∴DF=BE.(6分)
14.解:(1)旋转角的度数为60°.(3分)
(2)证明:由旋转的性质知∠ABC=∠A1BC1=120°,∠C=∠C1,AB=A1B.
∵点A,B,C1在同一直线上,∴∠ABC1=180°,
∴∠ABA1=∠CBC1=60°,∴∠A1BC=60°,
∵AB=A1B,∴△ABA1是等边三角形,(6分)
∴∠AA1B=∠A1BC=60°,∴AA1∥BC,∴∠A1AC=∠C.
又∵∠C=∠C1,∴∠A1AC=∠C1.(8分)
15.解:(1)∵将△ABD绕点A逆时针旋转,得到△ACD',
∴∠DAD'=∠BAC.
∵∠BAC=90°,∴∠DAD'=90°.(3分)
(2)证明:∵△ABD绕点A逆时针旋转得到△ACD',
∴AD=AD',∠DAD'=∠BAC=90°.
∵∠DAE=45°,∴∠D'AE=∠DAD'-∠DAE=90°-45°=45°,
∴∠D'AE=∠DAE.(5分)
在△AED与△AED'中,
∴△AED≌△AED'(SAS),∴DE=D'E.(8分)
16.解:将△BCE绕点C逆时针旋转90°,得到△ACF,作图如图所示:(2分)
连接DF.由旋转的性质,得CE=CF,AF=BE=2,∠ACF=∠BCE,∠CAF=∠B=45°.
∵∠ACB=90°,∠DCE=45°,
∴∠DCF=∠ACD+∠ACF=∠ACD+∠BCE=∠ACB-∠DCE=90°-45°=45°,
∴∠DCE=∠DCF.(4分)
在△CDE和△CDF中,
∴△CDE≌△CDF(SAS),∴DE=DF.(6分)
∵∠DAF=∠BAC+∠CAF=45°+45°=90°,
∴△ADF是直角三角形,∴DF2=AD2+AF2,
∴DE2=AD2+BE2=32+22=13,∴DE=.(8分)
17.解:(1)(1,-1) (-6,-5);(2分)
(2);(4分)
(3)设点D的坐标为(x,y).
若以AB为对角线,AC,BC为邻边的四边形为平行四边形,则AB,CD的中点重合,
∴解得(6分)
若以BC为对角线,AB,AC为邻边的四边形为平行四边形,则AD,BC的中点重合,
∴解得(8分)
若以AC为对角线,AB,BC为邻边的四边形为平行四边形,则BD,AC的中点重合,
∴解得
综上可知,点D的坐标为(1,-1)或(5,3)或(-3,5).(10分)
18.解:如图(1),是轴对称图形,又是中心对称图形;
如图(2),是轴对称图形,但不是中心对称图形;
如图(3),是中心对称图形,但不是轴对称图形.
每组画对一个即可,每个图形4分.
同课章节目录
