第二十三章 旋转 能力提优卷(含答案) 人教版九年级数学上册
文档属性
| 名称 | 第二十三章 旋转 能力提优卷(含答案) 人教版九年级数学上册 |  | |
| 格式 | docx | ||
| 文件大小 | 357.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-03-30 08:00:51 | ||
图片预览


文档简介
第二十三章 旋转
时间:60分钟 满分:100分
一、选择题(本题共6小题,每小题5分,共30分)
1.下列运动形式属于旋转的是 ( )
A.在空中上升的氢气球 B.飞驰的火车
C.时钟上钟摆的摆动 D.运动员掷出的标枪
2.围棋起源于中国,古代称之为“弈”,至今已有4000多年的历史.世界围棋冠军柯洁与人工智能机器人AlphaGo进行围棋人机大战.截取首局对战棋谱中的四个部分,由黑白棋子摆成的图案是中心对称的是 ( )
3.利用图形的旋转可以设计出许多美丽的图案.图2中的图案是由图1所示的基本图案以点O为旋转中心,顺时针(或逆时针)旋转角度α,依次旋转五次而组成的,则旋转角α的值不可能是 ( )
A.36° B.72° C.144° D.216°
4.如图,△ABC通过平移、轴对称或旋转得到△DEC,下列变换正确的是 ( )
A.△ABC绕点C顺时针旋转90°后再向左平移3个单位长度得△DEC
B.△ABC沿BC翻折后再绕点C逆时针旋转90°得到△DEC
C.△ABC沿AC翻折后再绕点C逆时针旋转90°得到△DEC
D.△ABC沿AC翻折后再绕点C顺时针旋转90°得到△DEC
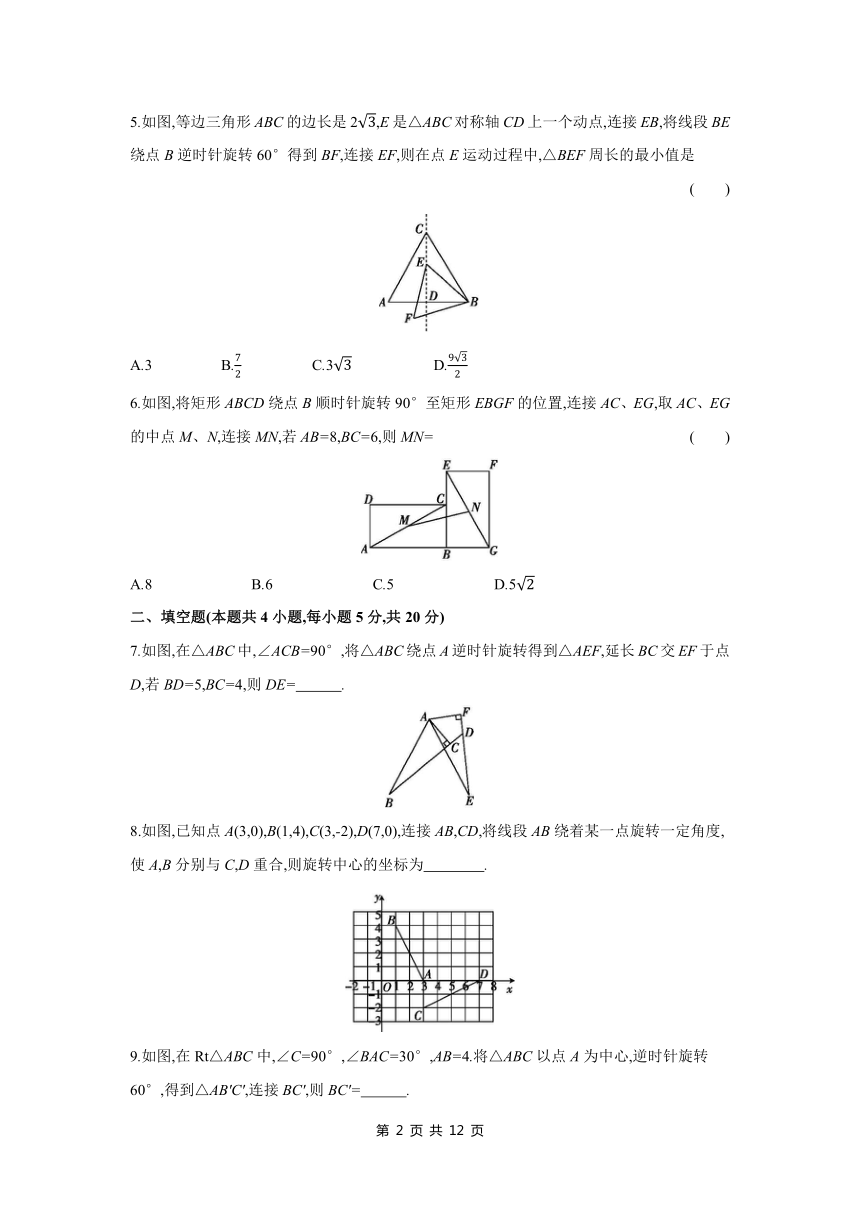
5.如图,等边三角形ABC的边长是2,E是△ABC对称轴CD上一个动点,连接EB,将线段BE绕点B逆时针旋转60°得到BF,连接EF,则在点E运动过程中,△BEF周长的最小值是 ( )
A.3 B. C.3 D.
6.如图,将矩形ABCD绕点B顺时针旋转90°至矩形EBGF的位置,连接AC、EG,取AC、EG的中点M、N,连接MN,若AB=8,BC=6,则MN= ( )
A.8 B.6 C.5 D.5
二、填空题(本题共4小题,每小题5分,共20分)
7.如图,在△ABC中,∠ACB=90°,将△ABC绕点A逆时针旋转得到△AEF,延长BC交EF于点D,若BD=5,BC=4,则DE= .
8.如图,已知点A(3,0),B(1,4),C(3,-2),D(7,0),连接AB,CD,将线段AB绕着某一点旋转一定角度,使A,B分别与C,D重合,则旋转中心的坐标为 .
9.如图,在Rt△ABC中,∠C=90°,∠BAC=30°,AB=4.将△ABC以点A为中心,逆时针旋转60°,得到△AB'C',连接BC',则BC'= .
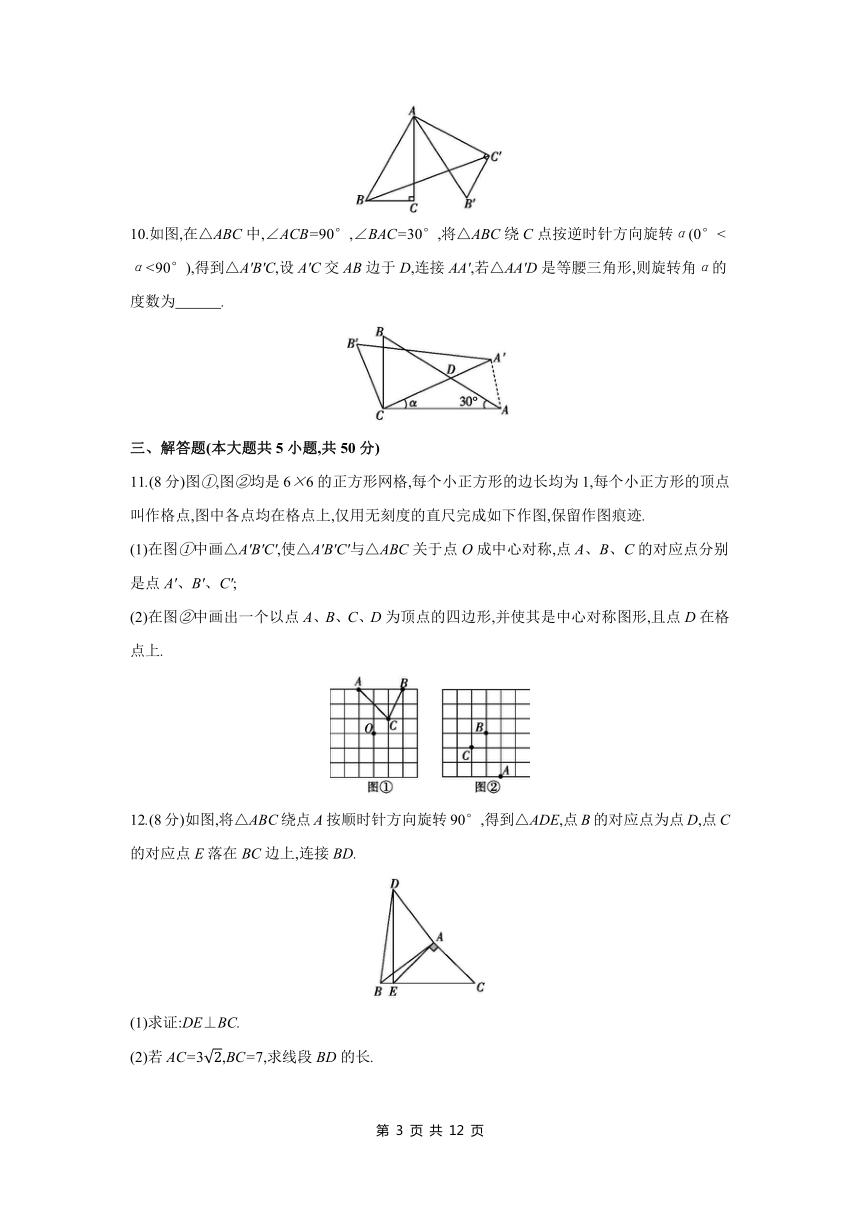
10.如图,在△ABC中,∠ACB=90°,∠BAC=30°,将△ABC绕C点按逆时针方向旋转α(0°<α<90°),得到△A'B'C,设A'C交AB边于D,连接AA',若△AA'D是等腰三角形,则旋转角α的度数为 .
三、解答题(本大题共5小题,共50分)
11.(8分)图①,图②均是6×6的正方形网格,每个小正方形的边长均为1,每个小正方形的顶点叫作格点,图中各点均在格点上,仅用无刻度的直尺完成如下作图,保留作图痕迹.
(1)在图①中画△A'B'C',使△A'B'C'与△ABC关于点O成中心对称,点A、B、C的对应点分别是点A'、B'、C';
(2)在图②中画出一个以点A、B、C、D为顶点的四边形,并使其是中心对称图形,且点D在格点上.
12.(8分)如图,将△ABC绕点A按顺时针方向旋转90°,得到△ADE,点B的对应点为点D,点C的对应点E落在BC边上,连接BD.
(1)求证:DE⊥BC.
(2)若AC=3,BC=7,求线段BD的长.
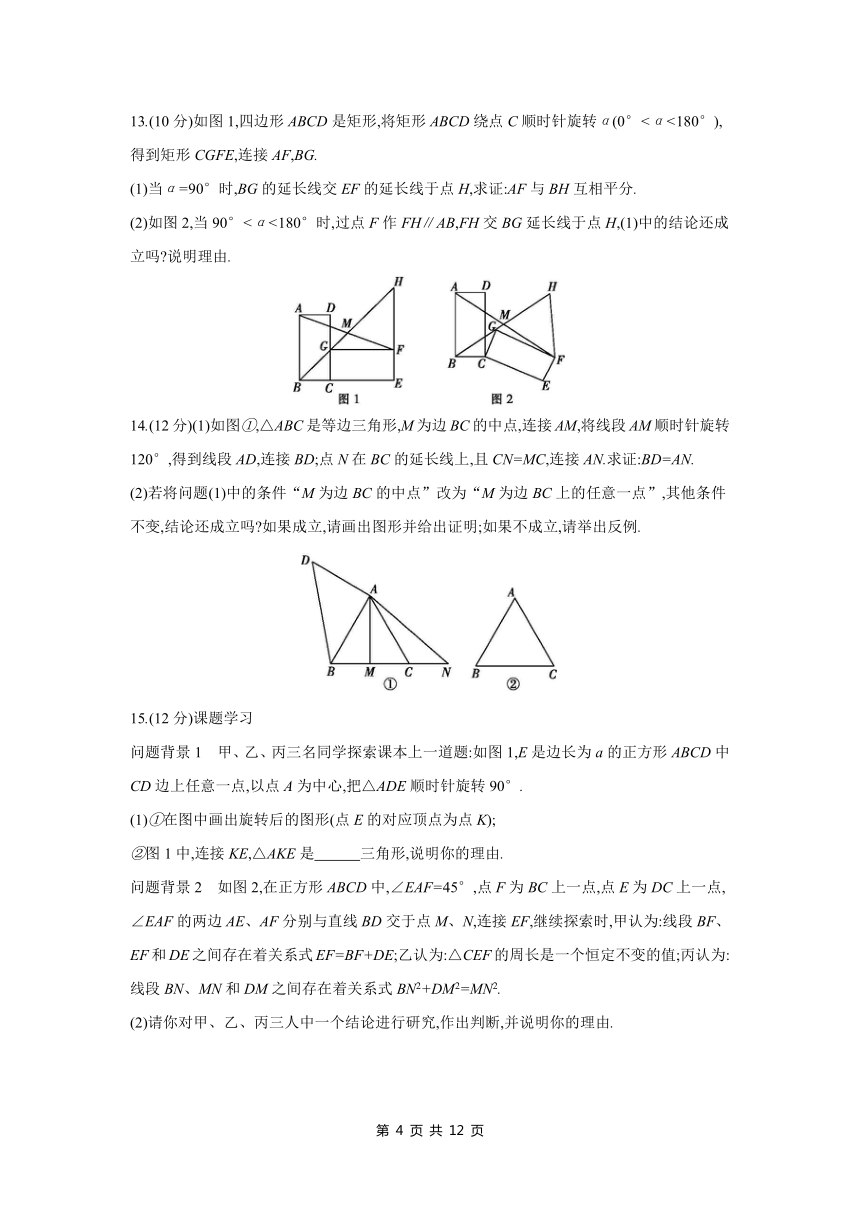
13.(10分)如图1,四边形ABCD是矩形,将矩形ABCD绕点C顺时针旋转α(0°<α<180°),得到矩形CGFE,连接AF,BG.
(1)当α=90°时,BG的延长线交EF的延长线于点H,求证:AF与BH互相平分.
(2)如图2,当90°<α<180°时,过点F作FH∥AB,FH交BG延长线于点H,(1)中的结论还成立吗 说明理由.
14.(12分)(1)如图①,△ABC是等边三角形,M为边BC的中点,连接AM,将线段AM顺时针旋转120°,得到线段AD,连接BD;点N在BC的延长线上,且CN=MC,连接AN.求证:BD=AN.
(2)若将问题(1)中的条件“M为边BC的中点”改为“M为边BC上的任意一点”,其他条件不变,结论还成立吗 如果成立,请画出图形并给出证明;如果不成立,请举出反例.
15.(12分)课题学习
问题背景1 甲、乙、丙三名同学探索课本上一道题:如图1,E是边长为a的正方形ABCD中CD边上任意一点,以点A为中心,把△ADE顺时针旋转90°.
(1)①在图中画出旋转后的图形(点E的对应顶点为点K);
②图1中,连接KE,△AKE是 三角形,说明你的理由.
问题背景2 如图2,在正方形ABCD中,∠EAF=45°,点F为BC上一点,点E为DC上一点,∠EAF的两边AE、AF分别与直线BD交于点M、N,连接EF,继续探索时,甲认为:线段BF、EF和DE之间存在着关系式EF=BF+DE;乙认为:△CEF的周长是一个恒定不变的值;丙认为:线段BN、MN和DM之间存在着关系式BN2+DM2=MN2.
(2)请你对甲、乙、丙三人中一个结论进行研究,作出判断,并说明你的理由.
参考答案
一、选择题
1 2 3 4 5 6
C A A C C D
3.A 【解析】根据题意,顺时针(或逆时针)旋转角度α,依次旋转五次而组成,这个图形可以由一个基本图形绕中心依次旋转五次而得到,每次旋转的度数为360°除以5,为72°,即旋转角是72°的倍数,故旋转角α的值不可能是36°.
4.C 【解析】根据旋转变换,翻折变换,平移变换的性质可知,△ABC沿AC翻折后再绕点C逆时针旋转90°得到△DEC.
5.C 【解析】∵将线段BE绕点B逆时针旋转60°得到BF,∴BE=BF,∠EBF=60°,∴△BEF是等边三角形,∴△BEF的周长=3BE,∴当BE取最小值时,△BEF的周长有最小值,∵等边三角形ABC的边长是2,CD为对称轴,∴AD=BD=,CD⊥AB,∵点E是△ABC对称轴CD上一个动点,∴BE⊥CD时,BE有最小值,∴△BEF周长的最小值为3.
6.D 【解析】如图,连接BD,BF,DF,∵四边形ABCD,四边形BEFG都是矩形,M、N是AC、EG的中点,∴点M是BD的中点,点N是BF的中点,∴MN=DF,∵AB=8,BC=6,∴AC=10,∴AC=BD=10,∵将矩形ABCD绕点B顺时针旋转90°至矩形EBGF的位置,∴DB=BF=10,∠DBF=90°,∴DF=BD=10,∴MN=5.
二、填空题
7 8 9 10
3 (2,-1) 2 20°或40°
7.3 【解析】连接AD.在Rt△ADF和Rt△ADC中,,∴Rt△ADF≌Rt△ADC(HL),∴DF=DC,∵BD=5,BC=4,∴CD=DF=5-4=1,∵EF=BC=4,∴DE=EF-DF=4-1=3.
8.(2,-1) 【解析】如图,连接BD,作线段BD,AC的垂直平分线交于点M,点M即为旋转中心,M(2,-1).
9.2 【解析】∵∠C=90°,∠BAC=30°,AB=4,∴BC=AB=2,AC=BC=2,∵将△ABC以点A为中心,逆时针旋转60°,得到△AB'C',∴AC=AC'=2,∠CAC'=60°,∴∠BAC'=90°,∴BC'===2.
10.20°或40° 【解析】∵△ABC绕C点逆时针方向旋转得到△A'B'C,∴AC=CA',∴∠AA'C=∠CAA'=(180°-α),∴∠DAA'=∠CAA'-∠BAC=(180°-α)-30°,根据三角形的外角性质,∠ADA'=∠BAC+∠ACA'=30°+α,△ADA'是等腰三角形,分三种情况讨论,①∠AA'C=∠DAA'时,(180°-α)=(180°-α)-30°,无解;②∠AA'C=∠ADA'时,(180°-α)=30°+α,解得α=40°;③∠DAA'=∠ADA'时,(180°-α)-30°=30°+α,解得α=20°.综上所述,旋转角α的度数为20°或40°.
三、解答题
11.解:(1)如图,△A'B'C'为所作;(4分)
(2)如图,四边形ACBD为所作(答案不唯一).(8分)
12.解:(1)∵将△ABC绕点A按顺时针方向旋转90°,
∴AC=AE,∠CAE=90°,∠AED=∠ACE,
∴∠ACE=∠AEC=45°=∠AED,
∴∠DEC=90°,
∴DE⊥BC.(4分)
(2)∵AE=AC=3,∠EAC=90°,
∴EC=6,∴BE=BC-EC=1,
∵将△ABC绕点A按顺时针方向旋转90°,
∴DE=BC=7,
∴DB===5.(8分)
13.解:(1)如图1,连接BF,AH,
∵将矩形ABCD绕点C顺时针旋转α(0°<α<180°),得到矩形CGFE,
∴BC=CG,CD=CE,
∵四边形ABCD和四边形CGFE是矩形,
∴AB=CD,CE=GF,∠ABC=∠CEF=90°,
∴AB=GF,HF∥AB,
∵∠BCG=90°,∴∠CBG=45°,
∴∠HGF=∠GHF=45°,
∴GF=HF,∴AB=HF,
∴四边形ABFH是平行四边形,
∴AF与BH互相平分;(4分)
(2)(1)中的结论还成立.
理由如下:如图2,连接BF,AH,
∵将矩形ABCD绕点C顺时针旋转α(0°<α<180°),得到矩形CGFE,
∴BC=CG,CD=CE,∴∠CBG=∠BGC,
∵四边形ABCD和四边形CGFE是矩形,
∴∠ABC=∠CGF=90°,AB=CD,CE=GF,
∴∠ABH+∠CBG=90°,∠BGC+∠HGF=90°,AB=GF,
∴∠ABH=∠HGF,
∵AB∥FH,∴∠ABH=∠GHF,∴∠HGF=∠GHF,
∴GF=HF,∴AB=HF,
∴四边形ABFH为平行四边形,
∴AF与BH互相平分.(10分)
14.解:(1)证明:∵△ABC是等边三角形,
∴∠ABC=∠BAC=∠ACB=60°,AB=BC=AC,
∵M是BC的中点,
∴∠AMB=∠AMN=90°,BC=2BM=2MC,∠BAM=∠BAC=30°,
∵AM顺时针旋转120°得到线段AD,
∴∠MAD=120°,AD=AM,
∴∠BAD=∠MAD-∠BAM=120°-30°=90°,
∴∠BAD=∠AMN=90°,
∵MC=CN,∴MN=2MC=BC=AB,
在△DBA和△ANM中,,
∴△DBA≌△ANM(SAS),
∴BD=AN.(5分)
(2)结论成立,理由如下:
①如图1中,当BM>BC时,分别过点A、点D作AG⊥BM、DH⊥BA,垂足分别为点G、H.
∴∠DHA=∠AGM=90°,
∵∠AMG+∠BAM+∠ABC=180°,∠ABC=60°,
∴∠AMG=180°-∠ABC-∠BAM=120°-∠BAM,
∵AM顺时针旋转120°得到线段AD,
∴∠MAD=120°,AD=AM,
∴∠DAB=120°-∠BAM,∴∠DAB=∠AMB,
在△DAH和△AMG中,,
∴△DAH≌△AMG(AAS),
∴DH=AG,AH=GM,
又∵△ABC是等边三角形,AG⊥BM,∴BG=GC,
∴GN=GC+CN=GC+CM=BG+GC-GM=BC-GM,
又∵BH=AB-HA,AH=GM,AB=BC,∴BH=GN.
∵DH=AG,∠DHB=∠AGM=90°,BH=GN,
在△DBH和△ANG中,,
∴△DBH≌△ANG(SAS),
∴BD=AN.(8分)
②当BM15.解:(1)①画图如图1所示:(3分)
②等腰直角.理由如下:
延长CB至K,使BK=DE,
∵四边形ABCD是正方形,
∴AD=AB,∠ADE=∠ABK=∠BAD=90°,
∴△ADE≌△ABK,
∴∠DAE=∠BAK,AK=AE,
∴∠EAK=∠BAK+∠BAE=∠DAE+∠BAE=∠BAD=90°,
∴AK⊥AE,∴△AKE是等腰直角三角形.(5分)
(2)选择甲发现:
证明:如图2,
延长CB到K,使BK=DE,连接AK,则△AKB≌△AED,
∵∠BAF+∠DAE=45°,∴∠KAF=45°,
∴∠KAF=∠FAE.
∵AK=AE,AF=AF,
∴△AKF≌△AEF.∴KF=EF.
又∵BK=DE,∴EF=BF+DE.(12分)
选择乙发现:
证明:如图3,
延长CB到K,使BK=DE,连接AK,则△AKB≌△AED,
∵∠BAF+∠DAE=45°,∴∠KAF=45°,∴∠KAF=∠FAE.
∵AK=AE,AF=AF,∴△AKF≌△AEF.∴KF=EF.
又∵BK=DE,∴EF=BF+DE.
△CEF周长=CF+CE+EF=CF+CE+(BF+DE)=(CF+BF)+(CE+DE)=BC+DC=2a(定值).(12分)
选择丙发现:
证明:如图4,
在AK上截取AG=AM,连接BG,GN.
∵AG=AM,AB=AD,∠KAB=∠EAD,
∴△ABG≌△ADM,
∴BG=DM,∠ABG=∠ADB=45°.
又∵∠ABD=45°,∴∠GBD=90°.
∵∠BAF+∠DAE=45°,∴∠KAF=45°,∴∠KAF=∠FAE.
又∵AG=AM,AN=AN,
∴△GAN≌△MAN.∴NG=MN,
∵∠GBD=90°,∴BG2+BN2=NG2,∴BN2+DM2=MN2.(12分)
时间:60分钟 满分:100分
一、选择题(本题共6小题,每小题5分,共30分)
1.下列运动形式属于旋转的是 ( )
A.在空中上升的氢气球 B.飞驰的火车
C.时钟上钟摆的摆动 D.运动员掷出的标枪
2.围棋起源于中国,古代称之为“弈”,至今已有4000多年的历史.世界围棋冠军柯洁与人工智能机器人AlphaGo进行围棋人机大战.截取首局对战棋谱中的四个部分,由黑白棋子摆成的图案是中心对称的是 ( )
3.利用图形的旋转可以设计出许多美丽的图案.图2中的图案是由图1所示的基本图案以点O为旋转中心,顺时针(或逆时针)旋转角度α,依次旋转五次而组成的,则旋转角α的值不可能是 ( )
A.36° B.72° C.144° D.216°
4.如图,△ABC通过平移、轴对称或旋转得到△DEC,下列变换正确的是 ( )
A.△ABC绕点C顺时针旋转90°后再向左平移3个单位长度得△DEC
B.△ABC沿BC翻折后再绕点C逆时针旋转90°得到△DEC
C.△ABC沿AC翻折后再绕点C逆时针旋转90°得到△DEC
D.△ABC沿AC翻折后再绕点C顺时针旋转90°得到△DEC
5.如图,等边三角形ABC的边长是2,E是△ABC对称轴CD上一个动点,连接EB,将线段BE绕点B逆时针旋转60°得到BF,连接EF,则在点E运动过程中,△BEF周长的最小值是 ( )
A.3 B. C.3 D.
6.如图,将矩形ABCD绕点B顺时针旋转90°至矩形EBGF的位置,连接AC、EG,取AC、EG的中点M、N,连接MN,若AB=8,BC=6,则MN= ( )
A.8 B.6 C.5 D.5
二、填空题(本题共4小题,每小题5分,共20分)
7.如图,在△ABC中,∠ACB=90°,将△ABC绕点A逆时针旋转得到△AEF,延长BC交EF于点D,若BD=5,BC=4,则DE= .
8.如图,已知点A(3,0),B(1,4),C(3,-2),D(7,0),连接AB,CD,将线段AB绕着某一点旋转一定角度,使A,B分别与C,D重合,则旋转中心的坐标为 .
9.如图,在Rt△ABC中,∠C=90°,∠BAC=30°,AB=4.将△ABC以点A为中心,逆时针旋转60°,得到△AB'C',连接BC',则BC'= .
10.如图,在△ABC中,∠ACB=90°,∠BAC=30°,将△ABC绕C点按逆时针方向旋转α(0°<α<90°),得到△A'B'C,设A'C交AB边于D,连接AA',若△AA'D是等腰三角形,则旋转角α的度数为 .
三、解答题(本大题共5小题,共50分)
11.(8分)图①,图②均是6×6的正方形网格,每个小正方形的边长均为1,每个小正方形的顶点叫作格点,图中各点均在格点上,仅用无刻度的直尺完成如下作图,保留作图痕迹.
(1)在图①中画△A'B'C',使△A'B'C'与△ABC关于点O成中心对称,点A、B、C的对应点分别是点A'、B'、C';
(2)在图②中画出一个以点A、B、C、D为顶点的四边形,并使其是中心对称图形,且点D在格点上.
12.(8分)如图,将△ABC绕点A按顺时针方向旋转90°,得到△ADE,点B的对应点为点D,点C的对应点E落在BC边上,连接BD.
(1)求证:DE⊥BC.
(2)若AC=3,BC=7,求线段BD的长.
13.(10分)如图1,四边形ABCD是矩形,将矩形ABCD绕点C顺时针旋转α(0°<α<180°),得到矩形CGFE,连接AF,BG.
(1)当α=90°时,BG的延长线交EF的延长线于点H,求证:AF与BH互相平分.
(2)如图2,当90°<α<180°时,过点F作FH∥AB,FH交BG延长线于点H,(1)中的结论还成立吗 说明理由.
14.(12分)(1)如图①,△ABC是等边三角形,M为边BC的中点,连接AM,将线段AM顺时针旋转120°,得到线段AD,连接BD;点N在BC的延长线上,且CN=MC,连接AN.求证:BD=AN.
(2)若将问题(1)中的条件“M为边BC的中点”改为“M为边BC上的任意一点”,其他条件不变,结论还成立吗 如果成立,请画出图形并给出证明;如果不成立,请举出反例.
15.(12分)课题学习
问题背景1 甲、乙、丙三名同学探索课本上一道题:如图1,E是边长为a的正方形ABCD中CD边上任意一点,以点A为中心,把△ADE顺时针旋转90°.
(1)①在图中画出旋转后的图形(点E的对应顶点为点K);
②图1中,连接KE,△AKE是 三角形,说明你的理由.
问题背景2 如图2,在正方形ABCD中,∠EAF=45°,点F为BC上一点,点E为DC上一点,∠EAF的两边AE、AF分别与直线BD交于点M、N,连接EF,继续探索时,甲认为:线段BF、EF和DE之间存在着关系式EF=BF+DE;乙认为:△CEF的周长是一个恒定不变的值;丙认为:线段BN、MN和DM之间存在着关系式BN2+DM2=MN2.
(2)请你对甲、乙、丙三人中一个结论进行研究,作出判断,并说明你的理由.
参考答案
一、选择题
1 2 3 4 5 6
C A A C C D
3.A 【解析】根据题意,顺时针(或逆时针)旋转角度α,依次旋转五次而组成,这个图形可以由一个基本图形绕中心依次旋转五次而得到,每次旋转的度数为360°除以5,为72°,即旋转角是72°的倍数,故旋转角α的值不可能是36°.
4.C 【解析】根据旋转变换,翻折变换,平移变换的性质可知,△ABC沿AC翻折后再绕点C逆时针旋转90°得到△DEC.
5.C 【解析】∵将线段BE绕点B逆时针旋转60°得到BF,∴BE=BF,∠EBF=60°,∴△BEF是等边三角形,∴△BEF的周长=3BE,∴当BE取最小值时,△BEF的周长有最小值,∵等边三角形ABC的边长是2,CD为对称轴,∴AD=BD=,CD⊥AB,∵点E是△ABC对称轴CD上一个动点,∴BE⊥CD时,BE有最小值,∴△BEF周长的最小值为3.
6.D 【解析】如图,连接BD,BF,DF,∵四边形ABCD,四边形BEFG都是矩形,M、N是AC、EG的中点,∴点M是BD的中点,点N是BF的中点,∴MN=DF,∵AB=8,BC=6,∴AC=10,∴AC=BD=10,∵将矩形ABCD绕点B顺时针旋转90°至矩形EBGF的位置,∴DB=BF=10,∠DBF=90°,∴DF=BD=10,∴MN=5.
二、填空题
7 8 9 10
3 (2,-1) 2 20°或40°
7.3 【解析】连接AD.在Rt△ADF和Rt△ADC中,,∴Rt△ADF≌Rt△ADC(HL),∴DF=DC,∵BD=5,BC=4,∴CD=DF=5-4=1,∵EF=BC=4,∴DE=EF-DF=4-1=3.
8.(2,-1) 【解析】如图,连接BD,作线段BD,AC的垂直平分线交于点M,点M即为旋转中心,M(2,-1).
9.2 【解析】∵∠C=90°,∠BAC=30°,AB=4,∴BC=AB=2,AC=BC=2,∵将△ABC以点A为中心,逆时针旋转60°,得到△AB'C',∴AC=AC'=2,∠CAC'=60°,∴∠BAC'=90°,∴BC'===2.
10.20°或40° 【解析】∵△ABC绕C点逆时针方向旋转得到△A'B'C,∴AC=CA',∴∠AA'C=∠CAA'=(180°-α),∴∠DAA'=∠CAA'-∠BAC=(180°-α)-30°,根据三角形的外角性质,∠ADA'=∠BAC+∠ACA'=30°+α,△ADA'是等腰三角形,分三种情况讨论,①∠AA'C=∠DAA'时,(180°-α)=(180°-α)-30°,无解;②∠AA'C=∠ADA'时,(180°-α)=30°+α,解得α=40°;③∠DAA'=∠ADA'时,(180°-α)-30°=30°+α,解得α=20°.综上所述,旋转角α的度数为20°或40°.
三、解答题
11.解:(1)如图,△A'B'C'为所作;(4分)
(2)如图,四边形ACBD为所作(答案不唯一).(8分)
12.解:(1)∵将△ABC绕点A按顺时针方向旋转90°,
∴AC=AE,∠CAE=90°,∠AED=∠ACE,
∴∠ACE=∠AEC=45°=∠AED,
∴∠DEC=90°,
∴DE⊥BC.(4分)
(2)∵AE=AC=3,∠EAC=90°,
∴EC=6,∴BE=BC-EC=1,
∵将△ABC绕点A按顺时针方向旋转90°,
∴DE=BC=7,
∴DB===5.(8分)
13.解:(1)如图1,连接BF,AH,
∵将矩形ABCD绕点C顺时针旋转α(0°<α<180°),得到矩形CGFE,
∴BC=CG,CD=CE,
∵四边形ABCD和四边形CGFE是矩形,
∴AB=CD,CE=GF,∠ABC=∠CEF=90°,
∴AB=GF,HF∥AB,
∵∠BCG=90°,∴∠CBG=45°,
∴∠HGF=∠GHF=45°,
∴GF=HF,∴AB=HF,
∴四边形ABFH是平行四边形,
∴AF与BH互相平分;(4分)
(2)(1)中的结论还成立.
理由如下:如图2,连接BF,AH,
∵将矩形ABCD绕点C顺时针旋转α(0°<α<180°),得到矩形CGFE,
∴BC=CG,CD=CE,∴∠CBG=∠BGC,
∵四边形ABCD和四边形CGFE是矩形,
∴∠ABC=∠CGF=90°,AB=CD,CE=GF,
∴∠ABH+∠CBG=90°,∠BGC+∠HGF=90°,AB=GF,
∴∠ABH=∠HGF,
∵AB∥FH,∴∠ABH=∠GHF,∴∠HGF=∠GHF,
∴GF=HF,∴AB=HF,
∴四边形ABFH为平行四边形,
∴AF与BH互相平分.(10分)
14.解:(1)证明:∵△ABC是等边三角形,
∴∠ABC=∠BAC=∠ACB=60°,AB=BC=AC,
∵M是BC的中点,
∴∠AMB=∠AMN=90°,BC=2BM=2MC,∠BAM=∠BAC=30°,
∵AM顺时针旋转120°得到线段AD,
∴∠MAD=120°,AD=AM,
∴∠BAD=∠MAD-∠BAM=120°-30°=90°,
∴∠BAD=∠AMN=90°,
∵MC=CN,∴MN=2MC=BC=AB,
在△DBA和△ANM中,,
∴△DBA≌△ANM(SAS),
∴BD=AN.(5分)
(2)结论成立,理由如下:
①如图1中,当BM>BC时,分别过点A、点D作AG⊥BM、DH⊥BA,垂足分别为点G、H.
∴∠DHA=∠AGM=90°,
∵∠AMG+∠BAM+∠ABC=180°,∠ABC=60°,
∴∠AMG=180°-∠ABC-∠BAM=120°-∠BAM,
∵AM顺时针旋转120°得到线段AD,
∴∠MAD=120°,AD=AM,
∴∠DAB=120°-∠BAM,∴∠DAB=∠AMB,
在△DAH和△AMG中,,
∴△DAH≌△AMG(AAS),
∴DH=AG,AH=GM,
又∵△ABC是等边三角形,AG⊥BM,∴BG=GC,
∴GN=GC+CN=GC+CM=BG+GC-GM=BC-GM,
又∵BH=AB-HA,AH=GM,AB=BC,∴BH=GN.
∵DH=AG,∠DHB=∠AGM=90°,BH=GN,
在△DBH和△ANG中,,
∴△DBH≌△ANG(SAS),
∴BD=AN.(8分)
②当BM
②等腰直角.理由如下:
延长CB至K,使BK=DE,
∵四边形ABCD是正方形,
∴AD=AB,∠ADE=∠ABK=∠BAD=90°,
∴△ADE≌△ABK,
∴∠DAE=∠BAK,AK=AE,
∴∠EAK=∠BAK+∠BAE=∠DAE+∠BAE=∠BAD=90°,
∴AK⊥AE,∴△AKE是等腰直角三角形.(5分)
(2)选择甲发现:
证明:如图2,
延长CB到K,使BK=DE,连接AK,则△AKB≌△AED,
∵∠BAF+∠DAE=45°,∴∠KAF=45°,
∴∠KAF=∠FAE.
∵AK=AE,AF=AF,
∴△AKF≌△AEF.∴KF=EF.
又∵BK=DE,∴EF=BF+DE.(12分)
选择乙发现:
证明:如图3,
延长CB到K,使BK=DE,连接AK,则△AKB≌△AED,
∵∠BAF+∠DAE=45°,∴∠KAF=45°,∴∠KAF=∠FAE.
∵AK=AE,AF=AF,∴△AKF≌△AEF.∴KF=EF.
又∵BK=DE,∴EF=BF+DE.
△CEF周长=CF+CE+EF=CF+CE+(BF+DE)=(CF+BF)+(CE+DE)=BC+DC=2a(定值).(12分)
选择丙发现:
证明:如图4,
在AK上截取AG=AM,连接BG,GN.
∵AG=AM,AB=AD,∠KAB=∠EAD,
∴△ABG≌△ADM,
∴BG=DM,∠ABG=∠ADB=45°.
又∵∠ABD=45°,∴∠GBD=90°.
∵∠BAF+∠DAE=45°,∴∠KAF=45°,∴∠KAF=∠FAE.
又∵AG=AM,AN=AN,
∴△GAN≌△MAN.∴NG=MN,
∵∠GBD=90°,∴BG2+BN2=NG2,∴BN2+DM2=MN2.(12分)
同课章节目录
