第二十四章 圆 能力提优卷 (含答案)人教版九年级数学上册
文档属性
| 名称 | 第二十四章 圆 能力提优卷 (含答案)人教版九年级数学上册 |  | |
| 格式 | docx | ||
| 文件大小 | 305.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-03-30 08:01:15 | ||
图片预览




文档简介
第二十四章 圆
时间:60分钟 满分:100分
一、选择题(本题共8小题,每小题4分,共32分)
1.下列说法正确的是 ( )
A.相等的圆心角所对的弧相等
B.平分弦的直径垂直弦并平分弦所对的弧
C.相等的弦所对的圆心角相等
D.等弧所对的弦相等
2.如图,一块直角三角板的60°的顶点A落在☉O上,两边分别交☉O于B,C两点,若☉O的半径是1,则的长是 ( )
A. B. C. D.
3.如图,在☉O中,=,过点A作BC的平行线交过点C的圆的切线于点D,若∠ABC=46°,则∠ADC的度数是 ( )
A.74° B.67° C.66° D.60°
4.嘉淇用一些完全相同的△ABC纸片拼接图案,已知用六个△ABC纸片按照图1所示的方法拼接可得外轮廓是正六边形的图案,若用n个△ABC纸片按图2所示的方法拼接,那么可以得到外轮廓的图案是 ( )
A.正十二边形 B.正十边形 C.正九边形 D.正八边形
5.已知☉O的半径为5,点O到直线l的距离为3,则☉O上到直线l的距离为2的点共有 ( )
A.1个 B.2个 C.3个 D.4个
6.如图所示,在矩形纸片ABCD中,AB=4 cm,把它分割成正方形纸片ABFE和矩形纸片EFCD后,分别裁出扇形ABF和半径最大的圆,恰好能作为一个圆锥的侧面和底面,则底面圆的直径的长为 ( )
A.2 cm B.3 cm C.4 cm D.5 cm
7.如图,AB是☉O的直径,点E是AB上一点,过点E作CD⊥AB,交☉O于点C,D,以下结论正确的是 ( )
A.若☉O的半径是2,点E是OB的中点,则CD=
B.若CD=,则☉O的半径是1
C.若∠CAB=30°,则四边形OCBD是菱形
D.若四边形OCBD是平行四边形,则∠CAB=60°
8.在《九章算术》卷九中记载了一个问题:“今有勾八步,股十五步,问勾中容圆径几何 ”其大意是:“如图,今有直角三角形,勾(短直角边)长为8步,股(长直角边)长为15步,问该直角三角形能容纳的圆(内切圆)的直径是多少步 ”根据题意,该内切圆的直径为 ( )
A.3步 B.4步 C.5步 D.6步
二、填空题(本题共4小题,每小题4分,共16分)
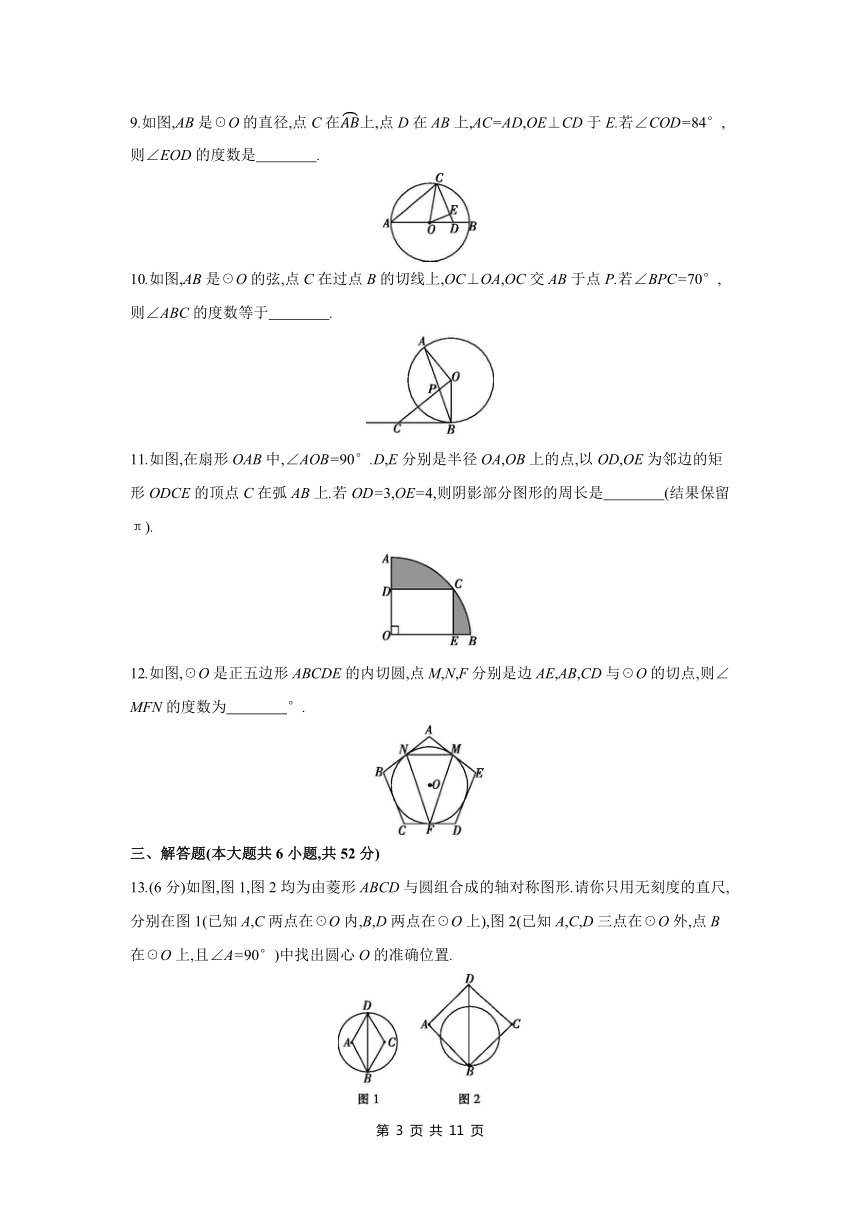
9.如图,AB是☉O的直径,点C在上,点D在AB上,AC=AD,OE⊥CD于E.若∠COD=84°,则∠EOD的度数是 .
10.如图,AB是☉O的弦,点C在过点B的切线上,OC⊥OA,OC交AB于点P.若∠BPC=70°,则∠ABC的度数等于 .
11.如图,在扇形OAB中,∠AOB=90°.D,E分别是半径OA,OB上的点,以OD,OE为邻边的矩形ODCE的顶点C在弧AB上.若OD=3,OE=4,则阴影部分图形的周长是 (结果保留π).
12.如图,☉O是正五边形ABCDE的内切圆,点M,N,F分别是边AE,AB,CD与☉O的切点,则∠MFN的度数为 °.
三、解答题(本大题共6小题,共52分)
13.(6分)如图,图1,图2均为由菱形ABCD与圆组合成的轴对称图形.请你只用无刻度的直尺,分别在图1(已知A,C两点在☉O内,B,D两点在☉O上),图2(已知A,C,D三点在☉O外,点B在☉O上,且∠A=90°)中找出圆心O的准确位置.
14.(8分)如图,∠EAD是☉O内接四边形ABCD的一个外角,且∠EAD=75°,DB=DC.
(1)求∠BDC的度数.
(2)若☉O的半径为2,求的长.
15.(8分)在☉O中,弦CD与直径AB相交于点P,∠ABC=64°.
(1)如图1,若∠APC=100°,求∠BAD和∠CDB的大小.
(2)如图2,若CD⊥AB,过点D作☉O的切线,与AB的延长线相交于点E,求∠E的大小.
16.(8分)如图,△ABC内接于☉O,点D在☉O上,且OD⊥BC,垂足为H,连接DC.
(1)求证:∠BCD=∠BAC.
(2)延长AB到点E,使EB=AC,连接DE.若DE与☉O相切,试判断四边形BCDE的形状,并说明理由.
17.(10分)如图,已知A,B是☉O上的点,P为☉O外一点,连接PA,PB,分别交☉O于点C,D,=.
(1)求证:PA=PB.
(2)若∠APB=60°,=3,△AOC的面积等于9,求图中阴影部分的面积.
18.(12分)如图,AB为☉O的直径,PD切☉O于点C,与BA的延长线交于点D,DE⊥PO交PO的延长线于点E,连接OC,PB,已知PB=6,DB=8,∠EDB=∠EPB.
(1)求证:PB是☉O的切线.
(2)求☉O的半径.
(3)连接BE,求BE的长.
参考答案
一、选择题
1 2 3 4 5 6 7 8
D C B C C A C D
1.D 【解析】A.在同圆或等圆中,相等的圆心角所对的弧相等,所以A选项的说法错误;B.平分弦(非直径)的直径垂直弦并平分弦所对的弧,所以B选项的说法错误;C.在同圆或等圆中,相等的弦所对的圆心角对应相等,所以C选项的说法错误;D.等弧所对的弦相等,所以D选项的说法正确.
2.C 【解析】连接OC,OB.∵∠BOC=2∠A=120°,∴的长==.
3.B 【解析】连接OA,∵=,∴∠BOC=∠AOB,∵OB=OC,OB=OA,∴∠BCO=∠OBC,∠OAB=∠OBA,∴∠OBA=∠CBO,∵∠ABC=46°,∴∠OCB=∠OBC=23°,∵CD是圆的切线,∴OC⊥CD,∴∠OCD=90°,∴∠BCD=∠BCO+∠OCD=113°,∵CB∥AD,∴∠ADC=180°-∠BCD=180°-113°=67°.
4.C 【解析】∵正六边形每一个内角为120°,∴∠ACB=120°-80°=40°,∴∠CAB=180°-120°=60°,∴图2中正多边形的每一个内角为60°+80°=140°,∵=9,∴可以得到外轮廓的图案是正九边形.
5.C 【解析】如图,∵☉O的半径为5,点O到直线l的距离为3,∴CE=2,过点D作AB⊥OC,垂足为D,交☉O于A、B两点,且DE=2,∴☉O上到直线l的距离为2的点为A、B、C,∴☉O上到直线l的距离为2的点有3个.
6.A 【解析】设圆锥的底面圆的半径为r cm,根据题意得=2πr,解得r=1,∴底面圆的直径为2 cm.
7.C 【解析】A.∵OC=OB=2,点E是OB的中点,∴OE=1,∵CD⊥AB,∴∠CEO=90°,CD=2CE,∴CE==,∴CD=2CE=2,本选项错误,不符合题意;B.根据CD=,缺少条件,无法得出半径是1,本选项错误,不符合题意;C.∵∠A=30°,∴∠COB=60°,∵OC=OB,∴△COB是等边三角形,∴BC=OC,∵CD⊥AB,∴CE=DE,∴BC=BD,∴OC=OD=BC=BD,∴四边形OCBD是菱形,故本选项正确,符合题意;D.∵四边形OCBD是平行四边形,∴OC=BC,∵OC=OB,∴OC=OB=BC,∴∠BOC=60°,∴∠CAB=∠BOC=30°,故本选项错误,不符合题意.
8.D 【解析】先利用勾股定理计算出斜边,直角三角形的斜边为=17,然后根据直角三角形的内切圆的半径为(a、b为直角边,c为斜边),得直角三角形的内切圆的半径==3,故直角三角形的内切圆的直径为6步.
二、填空题
9 10 11 12
21° 70° +10 36
9.21° 【解析】∵∠COD=84°,∴∠A=∠COD=42°.又∵AC=AD,∴∠ADC=∠ACD==69°.∵OE⊥CD,∴∠OED=90°,∴∠EOD=90°-69°=21°.
10.70° 【解析】∵BC为切线,∴OB⊥CB,∴∠OBC=90°,∵OC⊥OA,∴∠AOC=90°,∵∠OPA=∠BPC=70°,∴∠OAP=90°-70°=20°,∵OA=OB,∴∠OBA=∠OAB=20°,∴∠ABC=90°-∠OBA=90°-20°=70°.
11.+10 【解析】连接OC,∵四边形DOEC是矩形,OD=3,OE=4,∴EC=OD=3,∠OEC=90°,OE=CD=4,∴OC===5,∴阴影部分图形的周长是AD+DC+CE+BE+=(5-3)+4+3+(5-4)+=+10.
12.36 【解析】如图,连接OM,ON.∵M,N,F分别是AE,AB,CD与☉O的切点,∴OM⊥AE,ON⊥AB,∴∠OMA=∠ONA=90°,∵∠A=108°,∴∠MON=180°-108°=72°,∴∠MFN=∠MON=36°.
三、解答题
13.解:如图1,2,点O即为所求.(每小题3分)
14.解:(1)∵四边形ABCD是☉O的内接四边形,∴∠DAB+∠C=180°,
∵∠EAD+∠DAB=180°,∴∠C=∠EAD,
∵∠EAD=75°,∴∠C=75°,
∵DB=DC,∴∠DBC=∠C=75°,
∴∠BDC=180°-∠C-∠DBC=30°;(4分)
(2)连接OB、OC,
∵∠BDC=30°,∴∠BOC=2∠BDC=60°(圆周角定理),
∵☉O的半径为2,
∴的长是=.(8分)
15.解:(1)∵∠APC是△PBC的一个外角,
∴∠C=∠APC-∠ABC=100°-64°=36°,
由圆周角定理得∠BAD=∠C=36°,∠ADC=∠ABC=64°,
∵AB是☉O的直径,∴∠ADB=90°,
∴∠CDB=∠ADB-∠ADC=90°-64°=26°;(4分)
(2)连接OD,如图所示.
∵CD⊥AB,∴∠CPB=90°,
∴∠PCB=90°-∠ABC=90°-64°=26°,
∵DE是☉O的切线,∴DE⊥OD,∴∠ODE=90°,
∵∠BOD=2∠PCB=52°,
∴∠E=90°-∠BOD=90°-52°=38°.(8分)
16.解:(1)证明:如图,连接OB,OC,
∵OD⊥BC,∴==,
∴∠BCD=∠BAC;(4分)
(2)四边形BCDE是平行四边形,理由如下:
如图,连接BD,AD,
∵DE与☉O相切,∴OD⊥DE,
∵OD⊥BC,∴BC∥DE,
根据圆内接四边形的性质可知∠DBE=∠DCA,
在△DBE和△ACD中,,∴△DBE≌△DCA(SAS),
∴∠BED=∠DAC,(5分)
∵BC∥DE,∴∠BED=∠ABC=∠DAC,∴=,
∵=,∴∠BCD=∠CBD=∠ABC,∴EB∥CD,
∵BC∥DE,∴四边形BCDE是平行四边形.(8分)
17.解:(1)证明:连接OA,OC,OD,OB,作OM⊥AC于点M,ON⊥BD于点N.
∵=,∴AC=BD,
∵OA=OC=OB=OD,OM⊥AC,ON⊥BD,
∴CM=AM,BN=DN,∠OMC=∠OND=90°,
∴CM=DN,(3分)
在Rt△OMC和Rt△OND中,,
∴Rt△OMC≌Rt△OND(HL),∴OM=ON,
在Rt△POM和Rt△PON中,,
∴Rt△POM≌Rt△PON(HL),∴PM=PN,
∵AM=BN,∴PA=PB.(5分)
(2)∵∠APB=60°,∠PMO=∠PNO=90°,∴∠MON=120°,
∵△POM≌△PON,∴∠POM=∠PON=60°,
∵=3,∴∠COP=3∠COM,∴∠COM=15°,
∴∠AOC=2∠COM=30°,(8分)
过点A作AJ⊥OC于点J.设OA=OB=R,则AJ=R,
∵S△AOC=9,∴·R·R=9,∴R=6,
∴S阴影=S扇形AOC-S△AOC=-9=3π-9.(10分)
18.解:(1)证明:∵DE⊥PE,∴∠DEO=90°,
∵∠EDB=∠EPB,∠BOE=∠EDB+∠DEO,∠BOE=∠EPB+∠OBP,
∴∠OBP=∠DEO=90°,∴OB⊥PB,
∴PB为☉O的切线.(3分)
(2)在Rt△PBD中,PB=6,DB=8,
根据勾股定理得PD==10,
∵PD与PB都为☉O的切线,∴PC=PB=6,
∴DC=PD-PC=10-6=4;
在Rt△CDO中,设OC=r,则有OD=8-r,
根据勾股定理得(8-r)2=r2+42,解得r=3,
则圆O的半径为3.(7分)
(3)延长PB、DE相交于点F,
∵PD与PB都为☉O的切线,∴OP平分∠CPB,∴∠DPE=∠FPE,
∵PE⊥DF,∴∠PED=∠PEF=90°,
又∵PE=PE,∴△PED≌△PEF(ASA),
∴PF=PD=10,DE=EF,
∴BF=PF-PB=10-6=4,
在Rt△DBF中,DF===4,
∴BE=DF=2.(12分)
·
时间:60分钟 满分:100分
一、选择题(本题共8小题,每小题4分,共32分)
1.下列说法正确的是 ( )
A.相等的圆心角所对的弧相等
B.平分弦的直径垂直弦并平分弦所对的弧
C.相等的弦所对的圆心角相等
D.等弧所对的弦相等
2.如图,一块直角三角板的60°的顶点A落在☉O上,两边分别交☉O于B,C两点,若☉O的半径是1,则的长是 ( )
A. B. C. D.
3.如图,在☉O中,=,过点A作BC的平行线交过点C的圆的切线于点D,若∠ABC=46°,则∠ADC的度数是 ( )
A.74° B.67° C.66° D.60°
4.嘉淇用一些完全相同的△ABC纸片拼接图案,已知用六个△ABC纸片按照图1所示的方法拼接可得外轮廓是正六边形的图案,若用n个△ABC纸片按图2所示的方法拼接,那么可以得到外轮廓的图案是 ( )
A.正十二边形 B.正十边形 C.正九边形 D.正八边形
5.已知☉O的半径为5,点O到直线l的距离为3,则☉O上到直线l的距离为2的点共有 ( )
A.1个 B.2个 C.3个 D.4个
6.如图所示,在矩形纸片ABCD中,AB=4 cm,把它分割成正方形纸片ABFE和矩形纸片EFCD后,分别裁出扇形ABF和半径最大的圆,恰好能作为一个圆锥的侧面和底面,则底面圆的直径的长为 ( )
A.2 cm B.3 cm C.4 cm D.5 cm
7.如图,AB是☉O的直径,点E是AB上一点,过点E作CD⊥AB,交☉O于点C,D,以下结论正确的是 ( )
A.若☉O的半径是2,点E是OB的中点,则CD=
B.若CD=,则☉O的半径是1
C.若∠CAB=30°,则四边形OCBD是菱形
D.若四边形OCBD是平行四边形,则∠CAB=60°
8.在《九章算术》卷九中记载了一个问题:“今有勾八步,股十五步,问勾中容圆径几何 ”其大意是:“如图,今有直角三角形,勾(短直角边)长为8步,股(长直角边)长为15步,问该直角三角形能容纳的圆(内切圆)的直径是多少步 ”根据题意,该内切圆的直径为 ( )
A.3步 B.4步 C.5步 D.6步
二、填空题(本题共4小题,每小题4分,共16分)
9.如图,AB是☉O的直径,点C在上,点D在AB上,AC=AD,OE⊥CD于E.若∠COD=84°,则∠EOD的度数是 .
10.如图,AB是☉O的弦,点C在过点B的切线上,OC⊥OA,OC交AB于点P.若∠BPC=70°,则∠ABC的度数等于 .
11.如图,在扇形OAB中,∠AOB=90°.D,E分别是半径OA,OB上的点,以OD,OE为邻边的矩形ODCE的顶点C在弧AB上.若OD=3,OE=4,则阴影部分图形的周长是 (结果保留π).
12.如图,☉O是正五边形ABCDE的内切圆,点M,N,F分别是边AE,AB,CD与☉O的切点,则∠MFN的度数为 °.
三、解答题(本大题共6小题,共52分)
13.(6分)如图,图1,图2均为由菱形ABCD与圆组合成的轴对称图形.请你只用无刻度的直尺,分别在图1(已知A,C两点在☉O内,B,D两点在☉O上),图2(已知A,C,D三点在☉O外,点B在☉O上,且∠A=90°)中找出圆心O的准确位置.
14.(8分)如图,∠EAD是☉O内接四边形ABCD的一个外角,且∠EAD=75°,DB=DC.
(1)求∠BDC的度数.
(2)若☉O的半径为2,求的长.
15.(8分)在☉O中,弦CD与直径AB相交于点P,∠ABC=64°.
(1)如图1,若∠APC=100°,求∠BAD和∠CDB的大小.
(2)如图2,若CD⊥AB,过点D作☉O的切线,与AB的延长线相交于点E,求∠E的大小.
16.(8分)如图,△ABC内接于☉O,点D在☉O上,且OD⊥BC,垂足为H,连接DC.
(1)求证:∠BCD=∠BAC.
(2)延长AB到点E,使EB=AC,连接DE.若DE与☉O相切,试判断四边形BCDE的形状,并说明理由.
17.(10分)如图,已知A,B是☉O上的点,P为☉O外一点,连接PA,PB,分别交☉O于点C,D,=.
(1)求证:PA=PB.
(2)若∠APB=60°,=3,△AOC的面积等于9,求图中阴影部分的面积.
18.(12分)如图,AB为☉O的直径,PD切☉O于点C,与BA的延长线交于点D,DE⊥PO交PO的延长线于点E,连接OC,PB,已知PB=6,DB=8,∠EDB=∠EPB.
(1)求证:PB是☉O的切线.
(2)求☉O的半径.
(3)连接BE,求BE的长.
参考答案
一、选择题
1 2 3 4 5 6 7 8
D C B C C A C D
1.D 【解析】A.在同圆或等圆中,相等的圆心角所对的弧相等,所以A选项的说法错误;B.平分弦(非直径)的直径垂直弦并平分弦所对的弧,所以B选项的说法错误;C.在同圆或等圆中,相等的弦所对的圆心角对应相等,所以C选项的说法错误;D.等弧所对的弦相等,所以D选项的说法正确.
2.C 【解析】连接OC,OB.∵∠BOC=2∠A=120°,∴的长==.
3.B 【解析】连接OA,∵=,∴∠BOC=∠AOB,∵OB=OC,OB=OA,∴∠BCO=∠OBC,∠OAB=∠OBA,∴∠OBA=∠CBO,∵∠ABC=46°,∴∠OCB=∠OBC=23°,∵CD是圆的切线,∴OC⊥CD,∴∠OCD=90°,∴∠BCD=∠BCO+∠OCD=113°,∵CB∥AD,∴∠ADC=180°-∠BCD=180°-113°=67°.
4.C 【解析】∵正六边形每一个内角为120°,∴∠ACB=120°-80°=40°,∴∠CAB=180°-120°=60°,∴图2中正多边形的每一个内角为60°+80°=140°,∵=9,∴可以得到外轮廓的图案是正九边形.
5.C 【解析】如图,∵☉O的半径为5,点O到直线l的距离为3,∴CE=2,过点D作AB⊥OC,垂足为D,交☉O于A、B两点,且DE=2,∴☉O上到直线l的距离为2的点为A、B、C,∴☉O上到直线l的距离为2的点有3个.
6.A 【解析】设圆锥的底面圆的半径为r cm,根据题意得=2πr,解得r=1,∴底面圆的直径为2 cm.
7.C 【解析】A.∵OC=OB=2,点E是OB的中点,∴OE=1,∵CD⊥AB,∴∠CEO=90°,CD=2CE,∴CE==,∴CD=2CE=2,本选项错误,不符合题意;B.根据CD=,缺少条件,无法得出半径是1,本选项错误,不符合题意;C.∵∠A=30°,∴∠COB=60°,∵OC=OB,∴△COB是等边三角形,∴BC=OC,∵CD⊥AB,∴CE=DE,∴BC=BD,∴OC=OD=BC=BD,∴四边形OCBD是菱形,故本选项正确,符合题意;D.∵四边形OCBD是平行四边形,∴OC=BC,∵OC=OB,∴OC=OB=BC,∴∠BOC=60°,∴∠CAB=∠BOC=30°,故本选项错误,不符合题意.
8.D 【解析】先利用勾股定理计算出斜边,直角三角形的斜边为=17,然后根据直角三角形的内切圆的半径为(a、b为直角边,c为斜边),得直角三角形的内切圆的半径==3,故直角三角形的内切圆的直径为6步.
二、填空题
9 10 11 12
21° 70° +10 36
9.21° 【解析】∵∠COD=84°,∴∠A=∠COD=42°.又∵AC=AD,∴∠ADC=∠ACD==69°.∵OE⊥CD,∴∠OED=90°,∴∠EOD=90°-69°=21°.
10.70° 【解析】∵BC为切线,∴OB⊥CB,∴∠OBC=90°,∵OC⊥OA,∴∠AOC=90°,∵∠OPA=∠BPC=70°,∴∠OAP=90°-70°=20°,∵OA=OB,∴∠OBA=∠OAB=20°,∴∠ABC=90°-∠OBA=90°-20°=70°.
11.+10 【解析】连接OC,∵四边形DOEC是矩形,OD=3,OE=4,∴EC=OD=3,∠OEC=90°,OE=CD=4,∴OC===5,∴阴影部分图形的周长是AD+DC+CE+BE+=(5-3)+4+3+(5-4)+=+10.
12.36 【解析】如图,连接OM,ON.∵M,N,F分别是AE,AB,CD与☉O的切点,∴OM⊥AE,ON⊥AB,∴∠OMA=∠ONA=90°,∵∠A=108°,∴∠MON=180°-108°=72°,∴∠MFN=∠MON=36°.
三、解答题
13.解:如图1,2,点O即为所求.(每小题3分)
14.解:(1)∵四边形ABCD是☉O的内接四边形,∴∠DAB+∠C=180°,
∵∠EAD+∠DAB=180°,∴∠C=∠EAD,
∵∠EAD=75°,∴∠C=75°,
∵DB=DC,∴∠DBC=∠C=75°,
∴∠BDC=180°-∠C-∠DBC=30°;(4分)
(2)连接OB、OC,
∵∠BDC=30°,∴∠BOC=2∠BDC=60°(圆周角定理),
∵☉O的半径为2,
∴的长是=.(8分)
15.解:(1)∵∠APC是△PBC的一个外角,
∴∠C=∠APC-∠ABC=100°-64°=36°,
由圆周角定理得∠BAD=∠C=36°,∠ADC=∠ABC=64°,
∵AB是☉O的直径,∴∠ADB=90°,
∴∠CDB=∠ADB-∠ADC=90°-64°=26°;(4分)
(2)连接OD,如图所示.
∵CD⊥AB,∴∠CPB=90°,
∴∠PCB=90°-∠ABC=90°-64°=26°,
∵DE是☉O的切线,∴DE⊥OD,∴∠ODE=90°,
∵∠BOD=2∠PCB=52°,
∴∠E=90°-∠BOD=90°-52°=38°.(8分)
16.解:(1)证明:如图,连接OB,OC,
∵OD⊥BC,∴==,
∴∠BCD=∠BAC;(4分)
(2)四边形BCDE是平行四边形,理由如下:
如图,连接BD,AD,
∵DE与☉O相切,∴OD⊥DE,
∵OD⊥BC,∴BC∥DE,
根据圆内接四边形的性质可知∠DBE=∠DCA,
在△DBE和△ACD中,,∴△DBE≌△DCA(SAS),
∴∠BED=∠DAC,(5分)
∵BC∥DE,∴∠BED=∠ABC=∠DAC,∴=,
∵=,∴∠BCD=∠CBD=∠ABC,∴EB∥CD,
∵BC∥DE,∴四边形BCDE是平行四边形.(8分)
17.解:(1)证明:连接OA,OC,OD,OB,作OM⊥AC于点M,ON⊥BD于点N.
∵=,∴AC=BD,
∵OA=OC=OB=OD,OM⊥AC,ON⊥BD,
∴CM=AM,BN=DN,∠OMC=∠OND=90°,
∴CM=DN,(3分)
在Rt△OMC和Rt△OND中,,
∴Rt△OMC≌Rt△OND(HL),∴OM=ON,
在Rt△POM和Rt△PON中,,
∴Rt△POM≌Rt△PON(HL),∴PM=PN,
∵AM=BN,∴PA=PB.(5分)
(2)∵∠APB=60°,∠PMO=∠PNO=90°,∴∠MON=120°,
∵△POM≌△PON,∴∠POM=∠PON=60°,
∵=3,∴∠COP=3∠COM,∴∠COM=15°,
∴∠AOC=2∠COM=30°,(8分)
过点A作AJ⊥OC于点J.设OA=OB=R,则AJ=R,
∵S△AOC=9,∴·R·R=9,∴R=6,
∴S阴影=S扇形AOC-S△AOC=-9=3π-9.(10分)
18.解:(1)证明:∵DE⊥PE,∴∠DEO=90°,
∵∠EDB=∠EPB,∠BOE=∠EDB+∠DEO,∠BOE=∠EPB+∠OBP,
∴∠OBP=∠DEO=90°,∴OB⊥PB,
∴PB为☉O的切线.(3分)
(2)在Rt△PBD中,PB=6,DB=8,
根据勾股定理得PD==10,
∵PD与PB都为☉O的切线,∴PC=PB=6,
∴DC=PD-PC=10-6=4;
在Rt△CDO中,设OC=r,则有OD=8-r,
根据勾股定理得(8-r)2=r2+42,解得r=3,
则圆O的半径为3.(7分)
(3)延长PB、DE相交于点F,
∵PD与PB都为☉O的切线,∴OP平分∠CPB,∴∠DPE=∠FPE,
∵PE⊥DF,∴∠PED=∠PEF=90°,
又∵PE=PE,∴△PED≌△PEF(ASA),
∴PF=PD=10,DE=EF,
∴BF=PF-PB=10-6=4,
在Rt△DBF中,DF===4,
∴BE=DF=2.(12分)
·
同课章节目录
