专项训练卷(二)与圆有关的证明与计算 (含答案)人教版九年级数学上册
文档属性
| 名称 | 专项训练卷(二)与圆有关的证明与计算 (含答案)人教版九年级数学上册 |  | |
| 格式 | docx | ||
| 文件大小 | 243.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-03-30 08:10:17 | ||
图片预览


文档简介
专项训练卷(二)
时间:60分钟 满分:100分 范围:与圆有关的证明与计算
一、选择题(本题共8小题,每小题4分,共32分)
1.如图,点A,B,C,D,E在☉O上,AB=CD,∠AOB=42°,则∠CED= ( )
A.48° B.24° C.22° D.21°
2.如图,在Rt△ABC中,∠A=90°,BC=2,以BC的中点O为圆心的圆O分别与AB,AC相切于D,E两点,则的长为 ( )
A. B. C.π D.2π
3.已知锐角∠AOB=40°,如图,按下列步骤作图:①在OA边取一点D,以O为圆心,OD长为半径画,交OB于点C,连接CD.②以D为圆心,DO长为半径画,交OB于点E,连接DE.则∠CDE的度数为 ( )
A.20° B.30° C.40° D.50°
4.如图,在平面直角坐标系中,点P在第一象限,☉P与x轴、y轴都相切,且经过矩形AOBC的顶点C,与BC相交于点D.若☉P的半径为5,点A的坐标是(0,8),则点D的坐标是 ( )
A.(9,2) B.(9,3) C.(10,2) D.(10,3)
5.如图,在半径为5 cm的☉O中,将劣弧AB沿AB翻折,使折叠后的弧AB恰好与OA,OB相切,则劣弧AB的长为 ( )
A.π B.π C.π D.π
6.如图,在☉O中,AB切☉O于点A,连接OB交☉O于点C,过点A作AD∥OB交☉O于点D,连接CD.若∠B=50°,则∠OCD为 ( )
A.15° B.20° C.25° D.30°
7.如图,公园内有一个半径为18米的圆形草坪,从A地走到B地有观赏路(劣弧AB)和便民路(线段AB).已知A、B是圆上的点,O为圆心,∠AOB=120°,小强从A地走到B地,走便民路比走观赏路少走 ( )
A.(6π-6)米 B.(6π-9)米
C.(12π-9)米 D.(12π-18)米
8.如图,在Rt△ABC中,∠ACB=90°,以该三角形的三条边为边向外作正方形,正方形的顶点E,F,G,H,M,N都在同一个圆上.记该圆面积为S1,△ABC面积为S2,则的值是 ( )
A. B.3π C.5π D.
二、填空题(本题共4小题,每小题4分,共16分)
9.设圆锥的底面半径为2,母线长为3,该圆锥的侧面积为 .
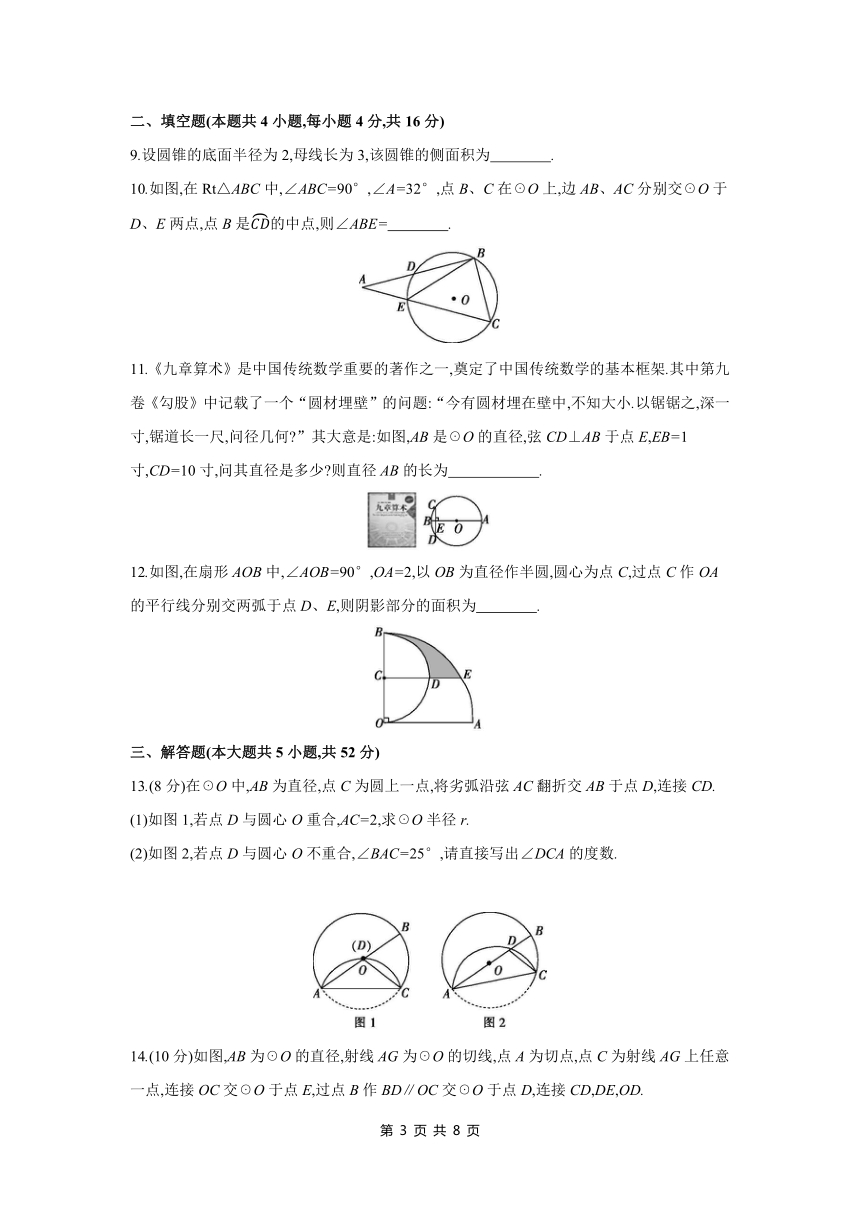
10.如图,在Rt△ABC中,∠ABC=90°,∠A=32°,点B、C在☉O上,边AB、AC分别交☉O于D、E两点,点B是的中点,则∠ABE= .
11.《九章算术》是中国传统数学重要的著作之一,奠定了中国传统数学的基本框架.其中第九卷《勾股》中记载了一个“圆材埋壁”的问题:“今有圆材埋在壁中,不知大小.以锯锯之,深一寸,锯道长一尺,问径几何 ”其大意是:如图,AB是☉O的直径,弦CD⊥AB于点E,EB=1寸,CD=10寸,问其直径是多少 则直径AB的长为 .
12.如图,在扇形AOB中,∠AOB=90°,OA=2,以OB为直径作半圆,圆心为点C,过点C作OA的平行线分别交两弧于点D、E,则阴影部分的面积为 .
三、解答题(本大题共5小题,共52分)
13.(8分)在☉O中,AB为直径,点C为圆上一点,将劣弧沿弦AC翻折交AB于点D,连接CD.
(1)如图1,若点D与圆心O重合,AC=2,求☉O半径r.
(2)如图2,若点D与圆心O不重合,∠BAC=25°,请直接写出∠DCA的度数.
14.(10分)如图,AB为☉O的直径,射线AG为☉O的切线,点A为切点,点C为射线AG上任意一点,连接OC交☉O于点E,过点B作BD∥OC交☉O于点D,连接CD,DE,OD.
(1)求证:△OAC≌△ODC.
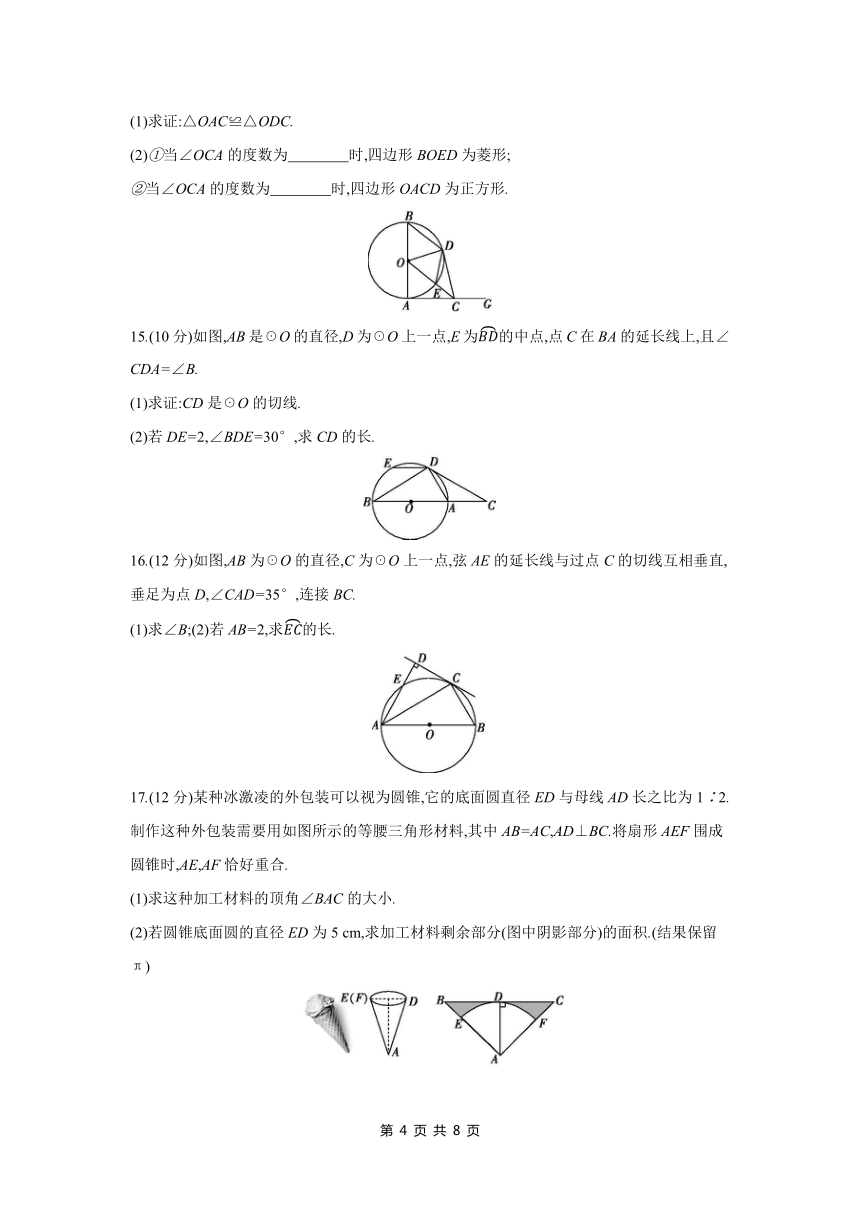
(2)①当∠OCA的度数为 时,四边形BOED为菱形;
②当∠OCA的度数为 时,四边形OACD为正方形.
15.(10分)如图,AB是☉O的直径,D为☉O上一点,E为的中点,点C在BA的延长线上,且∠CDA=∠B.
(1)求证:CD是☉O的切线.
(2)若DE=2,∠BDE=30°,求CD的长.
16.(12分)如图,AB为☉O的直径,C为☉O上一点,弦AE的延长线与过点C的切线互相垂直,垂足为点D,∠CAD=35°,连接BC.
(1)求∠B;(2)若AB=2,求的长.
17.(12分)某种冰激凌的外包装可以视为圆锥,它的底面圆直径ED与母线AD长之比为1∶2.制作这种外包装需要用如图所示的等腰三角形材料,其中AB=AC,AD⊥BC.将扇形AEF围成圆锥时,AE,AF恰好重合.
(1)求这种加工材料的顶角∠BAC的大小.
(2)若圆锥底面圆的直径ED为5 cm,求加工材料剩余部分(图中阴影部分)的面积.(结果保留π)
参考答案
一、选择题
1 2 3 4 5 6 7 8
D B B A B B D C
7.D 【解析】作OC⊥AB于点C,如图,则AC=BC,∵OA=OB,∴∠A=∠B=(180°-∠AOB)=30°,在Rt△AOC中,OC=OA=9米,∴AC==9(米),∴AB=2AC=18米,又∵==12π(米),∴走便民路比走观赏路少走(12π-18)米.
8.C 【解析】如图,设AB=c,AC=b,BC=a,则a2+b2=c2①,取AB的中点O,∵△ABC是直角三角形,∴OA=OB=OC,∵圆心在MN和HG的垂直平分线上,∴O为圆心,连接OC,OG,OE,作OD⊥AC,则OG,OE为半径,由勾股定理得r2=(a+)2+()2=c2+()2②,由①②得a=b,ab=,∴S1=πc2,S2=ab=,∴=5π.
二、填空题
9 10 11 12
6π 13° 26寸 π-
11.26寸 【解析】连接OC,∵弦CD⊥AB,AB为圆O的直径,∴E为CD的中点,又∵CD=10寸,∴CE=DE=CD=5寸.设OC=OA=x寸,则AB=2x寸,OE=(x-1)寸,由勾股定理得OE2+CE2=OC2,即(x-1)2+52=x2,解得x=13,∴AB=26寸.
12.π- 【解析】连接OE,根据题意可得出OB=OE=2,OC=1,∠OCE=90°,∴∠EOC=60°,CE=,∴S阴影=-×1×-=π-.
三、解答题
13.解:(1)如图,过圆心O作OE⊥AC于点F.
∵AC=2,∴AF=FC=1.在Rt△OFC中,∵OF=EF=r, OC=r,
∴由勾股定理得12+(r)2=r2,解得r=.即☉O的半径r为.(5分)
(2) ∠DCA的度数为40°.(8分)
14.解:(1)证明:∵OB=OD,∴∠B=∠ODB,
∵BD∥OC,∴∠AOC=∠B,∠DOC=∠ODB,
∴∠AOC=∠COD,
∵OA=OD,OC=OC,∴△OAC≌△ODC(SAS);(4分)
(2)①30°;(7分)
②45°.(10分)
15.解:(1)证明:连接OD,如图所示:
∵AB是直径,∴∠BDA=90°,∴∠BDO+∠ADO=90°,
又∵OB=OD,∠CDA=∠B,∴∠B=∠BDO=∠CDA,
∴∠CDA+∠ADO=90°,∴OD⊥CD,
又∵OD为☉O的半径,
∴CD是☉O的切线;(5分)
(2)连接OE,如图所示:
∵∠BDE=30°,∴∠BOE=2∠BDE=60°,
又∵点E为的中点,∴∠EOD=60°,
∴△EOD为等边三角形,∴ED=EO=OD=2,
又∵∠BOD=∠BOE+∠EOD=120°,
∴∠DOC=180°-∠BOD=180°-120°=60°,
在Rt△DOC中,∠DOC=60°,OD=2,
∴tan∠DOC=tan 60°===,∴CD=2.(10分)
16.解:(1)如图,连接OC,
∵CD为☉O的切线,∴OC⊥CD.
∵AD⊥CD,∴OC∥AD,∴∠CAD=∠ACO.
∵OA=OC,∴∠OAC=∠OCA,∴∠CAD=∠CAB=35°.
∵AB为☉O的直径,∴∠ACB=90°,∴∠B=55°.(8分)
(2)连接EO,∵∠CAD=35°,∴∠COE=70°,∴==.(12分)
17.解:(1)设∠BAC=n°.由题意得π·DE=,AD=2DE,
∴n=90,∴∠BAC=90°.(6分)
(2)∵AD=2DE=10(cm),
∴S阴影=·BC·AD-S扇形AEF=×10×20-=100-25π(cm2).(12分)
时间:60分钟 满分:100分 范围:与圆有关的证明与计算
一、选择题(本题共8小题,每小题4分,共32分)
1.如图,点A,B,C,D,E在☉O上,AB=CD,∠AOB=42°,则∠CED= ( )
A.48° B.24° C.22° D.21°
2.如图,在Rt△ABC中,∠A=90°,BC=2,以BC的中点O为圆心的圆O分别与AB,AC相切于D,E两点,则的长为 ( )
A. B. C.π D.2π
3.已知锐角∠AOB=40°,如图,按下列步骤作图:①在OA边取一点D,以O为圆心,OD长为半径画,交OB于点C,连接CD.②以D为圆心,DO长为半径画,交OB于点E,连接DE.则∠CDE的度数为 ( )
A.20° B.30° C.40° D.50°
4.如图,在平面直角坐标系中,点P在第一象限,☉P与x轴、y轴都相切,且经过矩形AOBC的顶点C,与BC相交于点D.若☉P的半径为5,点A的坐标是(0,8),则点D的坐标是 ( )
A.(9,2) B.(9,3) C.(10,2) D.(10,3)
5.如图,在半径为5 cm的☉O中,将劣弧AB沿AB翻折,使折叠后的弧AB恰好与OA,OB相切,则劣弧AB的长为 ( )
A.π B.π C.π D.π
6.如图,在☉O中,AB切☉O于点A,连接OB交☉O于点C,过点A作AD∥OB交☉O于点D,连接CD.若∠B=50°,则∠OCD为 ( )
A.15° B.20° C.25° D.30°
7.如图,公园内有一个半径为18米的圆形草坪,从A地走到B地有观赏路(劣弧AB)和便民路(线段AB).已知A、B是圆上的点,O为圆心,∠AOB=120°,小强从A地走到B地,走便民路比走观赏路少走 ( )
A.(6π-6)米 B.(6π-9)米
C.(12π-9)米 D.(12π-18)米
8.如图,在Rt△ABC中,∠ACB=90°,以该三角形的三条边为边向外作正方形,正方形的顶点E,F,G,H,M,N都在同一个圆上.记该圆面积为S1,△ABC面积为S2,则的值是 ( )
A. B.3π C.5π D.
二、填空题(本题共4小题,每小题4分,共16分)
9.设圆锥的底面半径为2,母线长为3,该圆锥的侧面积为 .
10.如图,在Rt△ABC中,∠ABC=90°,∠A=32°,点B、C在☉O上,边AB、AC分别交☉O于D、E两点,点B是的中点,则∠ABE= .
11.《九章算术》是中国传统数学重要的著作之一,奠定了中国传统数学的基本框架.其中第九卷《勾股》中记载了一个“圆材埋壁”的问题:“今有圆材埋在壁中,不知大小.以锯锯之,深一寸,锯道长一尺,问径几何 ”其大意是:如图,AB是☉O的直径,弦CD⊥AB于点E,EB=1寸,CD=10寸,问其直径是多少 则直径AB的长为 .
12.如图,在扇形AOB中,∠AOB=90°,OA=2,以OB为直径作半圆,圆心为点C,过点C作OA的平行线分别交两弧于点D、E,则阴影部分的面积为 .
三、解答题(本大题共5小题,共52分)
13.(8分)在☉O中,AB为直径,点C为圆上一点,将劣弧沿弦AC翻折交AB于点D,连接CD.
(1)如图1,若点D与圆心O重合,AC=2,求☉O半径r.
(2)如图2,若点D与圆心O不重合,∠BAC=25°,请直接写出∠DCA的度数.
14.(10分)如图,AB为☉O的直径,射线AG为☉O的切线,点A为切点,点C为射线AG上任意一点,连接OC交☉O于点E,过点B作BD∥OC交☉O于点D,连接CD,DE,OD.
(1)求证:△OAC≌△ODC.
(2)①当∠OCA的度数为 时,四边形BOED为菱形;
②当∠OCA的度数为 时,四边形OACD为正方形.
15.(10分)如图,AB是☉O的直径,D为☉O上一点,E为的中点,点C在BA的延长线上,且∠CDA=∠B.
(1)求证:CD是☉O的切线.
(2)若DE=2,∠BDE=30°,求CD的长.
16.(12分)如图,AB为☉O的直径,C为☉O上一点,弦AE的延长线与过点C的切线互相垂直,垂足为点D,∠CAD=35°,连接BC.
(1)求∠B;(2)若AB=2,求的长.
17.(12分)某种冰激凌的外包装可以视为圆锥,它的底面圆直径ED与母线AD长之比为1∶2.制作这种外包装需要用如图所示的等腰三角形材料,其中AB=AC,AD⊥BC.将扇形AEF围成圆锥时,AE,AF恰好重合.
(1)求这种加工材料的顶角∠BAC的大小.
(2)若圆锥底面圆的直径ED为5 cm,求加工材料剩余部分(图中阴影部分)的面积.(结果保留π)
参考答案
一、选择题
1 2 3 4 5 6 7 8
D B B A B B D C
7.D 【解析】作OC⊥AB于点C,如图,则AC=BC,∵OA=OB,∴∠A=∠B=(180°-∠AOB)=30°,在Rt△AOC中,OC=OA=9米,∴AC==9(米),∴AB=2AC=18米,又∵==12π(米),∴走便民路比走观赏路少走(12π-18)米.
8.C 【解析】如图,设AB=c,AC=b,BC=a,则a2+b2=c2①,取AB的中点O,∵△ABC是直角三角形,∴OA=OB=OC,∵圆心在MN和HG的垂直平分线上,∴O为圆心,连接OC,OG,OE,作OD⊥AC,则OG,OE为半径,由勾股定理得r2=(a+)2+()2=c2+()2②,由①②得a=b,ab=,∴S1=πc2,S2=ab=,∴=5π.
二、填空题
9 10 11 12
6π 13° 26寸 π-
11.26寸 【解析】连接OC,∵弦CD⊥AB,AB为圆O的直径,∴E为CD的中点,又∵CD=10寸,∴CE=DE=CD=5寸.设OC=OA=x寸,则AB=2x寸,OE=(x-1)寸,由勾股定理得OE2+CE2=OC2,即(x-1)2+52=x2,解得x=13,∴AB=26寸.
12.π- 【解析】连接OE,根据题意可得出OB=OE=2,OC=1,∠OCE=90°,∴∠EOC=60°,CE=,∴S阴影=-×1×-=π-.
三、解答题
13.解:(1)如图,过圆心O作OE⊥AC于点F.
∵AC=2,∴AF=FC=1.在Rt△OFC中,∵OF=EF=r, OC=r,
∴由勾股定理得12+(r)2=r2,解得r=.即☉O的半径r为.(5分)
(2) ∠DCA的度数为40°.(8分)
14.解:(1)证明:∵OB=OD,∴∠B=∠ODB,
∵BD∥OC,∴∠AOC=∠B,∠DOC=∠ODB,
∴∠AOC=∠COD,
∵OA=OD,OC=OC,∴△OAC≌△ODC(SAS);(4分)
(2)①30°;(7分)
②45°.(10分)
15.解:(1)证明:连接OD,如图所示:
∵AB是直径,∴∠BDA=90°,∴∠BDO+∠ADO=90°,
又∵OB=OD,∠CDA=∠B,∴∠B=∠BDO=∠CDA,
∴∠CDA+∠ADO=90°,∴OD⊥CD,
又∵OD为☉O的半径,
∴CD是☉O的切线;(5分)
(2)连接OE,如图所示:
∵∠BDE=30°,∴∠BOE=2∠BDE=60°,
又∵点E为的中点,∴∠EOD=60°,
∴△EOD为等边三角形,∴ED=EO=OD=2,
又∵∠BOD=∠BOE+∠EOD=120°,
∴∠DOC=180°-∠BOD=180°-120°=60°,
在Rt△DOC中,∠DOC=60°,OD=2,
∴tan∠DOC=tan 60°===,∴CD=2.(10分)
16.解:(1)如图,连接OC,
∵CD为☉O的切线,∴OC⊥CD.
∵AD⊥CD,∴OC∥AD,∴∠CAD=∠ACO.
∵OA=OC,∴∠OAC=∠OCA,∴∠CAD=∠CAB=35°.
∵AB为☉O的直径,∴∠ACB=90°,∴∠B=55°.(8分)
(2)连接EO,∵∠CAD=35°,∴∠COE=70°,∴==.(12分)
17.解:(1)设∠BAC=n°.由题意得π·DE=,AD=2DE,
∴n=90,∴∠BAC=90°.(6分)
(2)∵AD=2DE=10(cm),
∴S阴影=·BC·AD-S扇形AEF=×10×20-=100-25π(cm2).(12分)
同课章节目录
