专项训练卷(三)反比例函数与一次函数或几何图形的结合 (含答案) 人教版九年级数学下册
文档属性
| 名称 | 专项训练卷(三)反比例函数与一次函数或几何图形的结合 (含答案) 人教版九年级数学下册 |  | |
| 格式 | docx | ||
| 文件大小 | 193.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-03-30 08:10:29 | ||
图片预览



文档简介
专项训练卷(三)
时间:60分钟 满分:100分 范围:反比例函数与一次函数或几何图形的结合
一、选择题(本题共6小题,每小题5分,共30分)
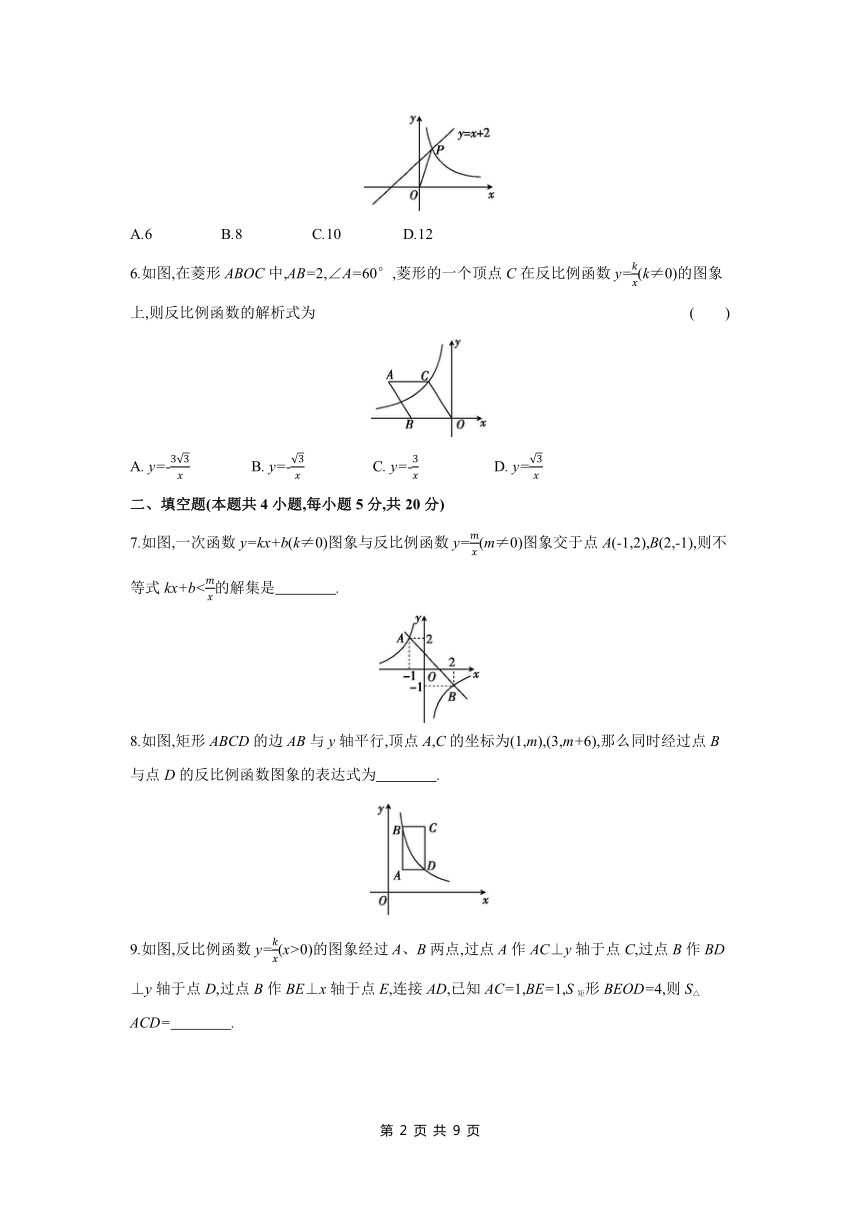
1.反比例函数y=与一次函数y=-x+2的图象的交点个数是 ( )
A.3 B.2 C.1 D.0
2.如图,一次函数y=kx+b(k、b为常数,且k≠0)和反比例函数y=(x>0)的图象交于A、B两点,利用函数图象可知不等式>kx+b的解集是 ( )
A.x<1 B.x>4 C.14
3.函数y=kx-k与y=在同一坐标系中的图象如图所示,下列结论正确的是 ( )
A.<0 B.km>0 C.m>0 D.k<0
4.如图,点A是反比例函数y=图象上的一点,过点A作AC⊥x轴,垂足为C,D为AC的中点,若△AOD的面积为1,则k的值为 ( )
A. B. C. 3 D. 4
5.如图,直线y=x+2与反比例函数y=的图象在第一象限交于点P.若OP=,则k的值为 ( )
A.6 B.8 C.10 D.12
6.如图,在菱形ABOC中,AB=2,∠A=60°,菱形的一个顶点C在反比例函数y=(k≠0)的图象上,则反比例函数的解析式为 ( )
A. y=- B. y=- C. y=- D. y=
二、填空题(本题共4小题,每小题5分,共20分)
7.如图,一次函数y=kx+b(k≠0)图象与反比例函数y=(m≠0)图象交于点A(-1,2),B(2,-1),则不等式kx+b<的解集是 .
8.如图,矩形ABCD的边AB与y轴平行,顶点A,C的坐标为(1,m),(3,m+6),那么同时经过点B与点D的反比例函数图象的表达式为 .
9.如图,反比例函数y=(x>0)的图象经过A、B两点,过点A作AC⊥y轴于点C,过点B作BD⊥y轴于点D,过点B作BE⊥x轴于点E,连接AD,已知AC=1,BE=1,S矩形BEOD=4,则S△ACD= .
10.如图,正比例函数y=x与反比例函数y=(x>0)的图象交于点A,过点A作AB⊥y轴于点B,点C在线段AB上,且AC=OC.点P为y轴上一动点,当△POC与△PAC的面积相等时,点P的坐标为 .
三、解答题(本大题共5小题,共50分)
11.(8分)如图,一次函数y=kx+b(k≠0)的图象与反比例函数y=(m≠0)的图象相交于点A(1,2),B(a,-1).
(1)求反比例函数和一次函数的解析式.
(2)若直线y=kx+b(k≠0)与x轴交于点C,x轴上是否存在一点P,使S△APC=4 若存在,请求出点P坐标;若不存在,说明理由.
12.(10分)如图,在平面直角坐标系中,直线y=-nx+12(n≠0)与坐标轴的正半轴相交于A,B两点,与反比例函数y=的图象相交于第一象限内的C,D两点,点C,D是线段AB的三等分点.
(1)用含n的代数式表示点B的坐标;
(2)若n=2,求反比例函数y=的解析式.
13.(10分)如图,在平面直角坐标系中,点M为OA的中点,AB⊥x轴于点B,反比例函数y=(k>0,x>0)的图象经过点M,交AB于点C.
(1)若点A的坐标为(2,6),则k= .点C的坐标为 ;
(2)连接MC,OC,若△OMC的面积为3,求k的值.
14.(10分)如图,经过原点O的直线与反比例函数y=(a>0)的图象交于A、D两点(点A在第一象限),点B、C、E在反比例函数y=(b<0)的图象上,AB∥y轴,AE∥CD∥x轴,五边形ABCDE的面积为56,四边形ABCD的面积为32.求下列各式的值:
(1)a-b; (2).
15.(12分)如图,在平面直角坐标系xOy中,△OA1B1是等边三角形,点B1的坐标是(2,0),反比例函数y=的图象经过点A1.
(1)求反比例函数的解析式.
(2)如图,以B1为顶点作等边三角形B1A2B2,使点B2在x轴上,点A2在反比例函数y=的图象上.若要使点B2在反比例函数y=的图象上,需将△B1A2B2向上平移多少个单位长度
参考答案
一、选择题
1 2 3 4 5 6
C D A D B B
4. D 【解析】∵AC⊥x轴,∴S△AOC=OC·AC=|k|.∵点D是AC的中点,S△AOD=1,∴S△AOC=2S△AOD=2,∴|k|=2,即|k|=4.∵k>0,∴k=4.
5.B 【解析】设点P(m,m+2),∵OP=,∴=,解得m1=2,m2=-4(不合题意舍去),∴点P(2,4),∴4=,解得k=8.
6.B 【解析】如图,过点C作CE⊥x轴于点E,∵四边形ABOC是菱形,AB=2,∠A=60°,∴OC=2,∠COE=60°,∴OE=OC·cos 60°=1,CE=OC·sin 60°=,∴C(-1,),∴k=-,∴反比例函数的解析式为y=-.
二、填空题
7 8 9 10
-12 y= (0,10)或(0,)
8.y= 【解析】∵矩形ABCD的边AB与y轴平行,A(1,m),C(3,m+6),∴B(1,m+6),D(3,m),∵B、D在反比例函数图象上,∴1×(m+6)=3m,解得m=3,∴B(1,9),故反比例函数表达式为y=.
9. 【解析】∵S矩形BDOE=|k|=4,k>0,∴k=4,∵AC=1,令x=1,则=y,解得y==4,∴A(1,4),∴OC=4,∵OD=BE=1,∴CD=OC-OD=4-1=3,∴S△ACD=CD·AC=×3×1=.
10.(0,10)或(0,) 【解析】由,得或,∴A(8,4),∵点C在线段AB上,且AC=OC.设点C(c,4),∵OC==,AC=AB-BC=8-c,∴=8-c,解得c=3,∴点C(3,4),∴BC=3,设点P(0,p),当点P为B点上方时,∴OP=p,BP=p-4,∵A(8,4),C(3,4),∴AC=8-3=5,BC=3,∵△POC与△PAC的面积相等,∴×3p=×5(p-4),解得p=10,∴P(0,10).当点P为B点下方时,∴OP=|p|,BP=4-p,∴×3|p|=×5(4-p),解得p=,∴P(0,).综上,点P的坐标为(0,10)或(0,).
三、解答题
11.解:(1)把点A(1,2)代入y=,得2=,∴m=2,
∴反比例函数的解析式为y=;(2分)
把B(a,-1)代入y=,得a=-2,∴B(-2,-1),
把点A(1,2),B(-2,-1)代入y=kx+b,得,解得.
∴一次函数的解析式为y=x+1;(4分)
(2)当y=0时,0=x+1,解得x=-1,∴C(-1,0),
设P(x,0),∴S△APC=×|x+1|×2=4,∴x=3或x=-5,
∴P(3,0)或(-5,0).(8分)
12.解:(1)∵直线y=-nx+12(n≠0)与坐标轴的正半轴相交于A,B两点,
∴令y=0,则0=-nx+12,∴x=,∴B(,0); (4分)
(2)作DE⊥x轴于点E,n=2,则y=-2x+12,
∴B(6,0),∴OB=6,
∵点C,D是AB的三等分点,∴OE=4,
把x=4代入y=-2x+12,得y=4,∴D(4,4),
∵D在反比例函数y=的图象上,∴k=4×4=16,
∴反比例函数解析式为y=.(10分)
13.解:(1)过点M作MD⊥x轴于点D,如图,
∵点A的坐标为(2,6),∴OB=2,AB=6.
∵AB⊥OB,MD⊥OB,∴MD∥AB.
∵点M为OA的中点,∴OD=OB=1,MD=AB=3.
∴M(1,3).∴k=1×3=3.当x=2时,y=.∴C(2,).
故答案为3;(2,).(5分)
(2)设M(a,b),则OD=a,MD=b,k=ab.
由(1)知:OB=2OD=2a,AB=2MD=2b.∴A(2a,2b).
∵AB⊥OB,∴C点的横坐标为2a,
∴C(2a,).
∴BC=.∴AC=AB-BC=2b-.
∵S△OMC=3,OM=AM,∴S△AOC=2×3=6.
∴AC×OB=6.∴×2a×(2b-)=6.∴2ab-k=6.
即2k-k=6.解得k=4.(10分)
14.解:(1)如图,连接EC,AC,设A(m,),
∵AE∥DC∥x轴,∴可得E(,),
∵五边形ABCDE的面积为56,四边形ABCD的面积为32,
∴S△AED=24,即·(m-)·=24,∴a-b=24;(5分)
(2)由反比例函数图象的对称性得,AO=DO,EO=OC,
∴四边形AEDC为平行四边形,∴S△ABC=56-2×24=8,C(-,-),
∵AB∥y轴,∴B(m,),∴·(-)·(m+)=8,即(a-b)·(1+)=16,
∵a-b=24,∴1+=,∴=-.(10分)
15.解:(1)如图1,过点A1作A1H⊥x轴于点H.
∵△OA1B1是等边三角形,点B1的坐标是(2,0),∴OA1=OB1=2,OH=1,
∴A1H===,∴A1(1,).
∵点A1在反比例函数y=的图象上,∴k=.
∴反比例函数的解析式为y=;(5分)
(2)如图2,过点A2作A2G⊥x轴于点G,设B1G=a,则A2G=a,∴A2(2+a,a).
∵点A2在反比例函数y=的图象上,∴a=,
解得a1=-1,a2=--1(不合题意,舍去),∴a=-1,
∴△B1A2B2的边长是2(-1),
∴B2(2,0),
∴把x=2代入y=,得y==,
∴(2,)在反比例函数y=的图象上,
∴若要使点B2在反比例函数y=的图象上,需将△B1A2B2向上平移个单位长度.(12分)
时间:60分钟 满分:100分 范围:反比例函数与一次函数或几何图形的结合
一、选择题(本题共6小题,每小题5分,共30分)
1.反比例函数y=与一次函数y=-x+2的图象的交点个数是 ( )
A.3 B.2 C.1 D.0
2.如图,一次函数y=kx+b(k、b为常数,且k≠0)和反比例函数y=(x>0)的图象交于A、B两点,利用函数图象可知不等式>kx+b的解集是 ( )
A.x<1 B.x>4 C.1
3.函数y=kx-k与y=在同一坐标系中的图象如图所示,下列结论正确的是 ( )
A.<0 B.km>0 C.m>0 D.k<0
4.如图,点A是反比例函数y=图象上的一点,过点A作AC⊥x轴,垂足为C,D为AC的中点,若△AOD的面积为1,则k的值为 ( )
A. B. C. 3 D. 4
5.如图,直线y=x+2与反比例函数y=的图象在第一象限交于点P.若OP=,则k的值为 ( )
A.6 B.8 C.10 D.12
6.如图,在菱形ABOC中,AB=2,∠A=60°,菱形的一个顶点C在反比例函数y=(k≠0)的图象上,则反比例函数的解析式为 ( )
A. y=- B. y=- C. y=- D. y=
二、填空题(本题共4小题,每小题5分,共20分)
7.如图,一次函数y=kx+b(k≠0)图象与反比例函数y=(m≠0)图象交于点A(-1,2),B(2,-1),则不等式kx+b<的解集是 .
8.如图,矩形ABCD的边AB与y轴平行,顶点A,C的坐标为(1,m),(3,m+6),那么同时经过点B与点D的反比例函数图象的表达式为 .
9.如图,反比例函数y=(x>0)的图象经过A、B两点,过点A作AC⊥y轴于点C,过点B作BD⊥y轴于点D,过点B作BE⊥x轴于点E,连接AD,已知AC=1,BE=1,S矩形BEOD=4,则S△ACD= .
10.如图,正比例函数y=x与反比例函数y=(x>0)的图象交于点A,过点A作AB⊥y轴于点B,点C在线段AB上,且AC=OC.点P为y轴上一动点,当△POC与△PAC的面积相等时,点P的坐标为 .
三、解答题(本大题共5小题,共50分)
11.(8分)如图,一次函数y=kx+b(k≠0)的图象与反比例函数y=(m≠0)的图象相交于点A(1,2),B(a,-1).
(1)求反比例函数和一次函数的解析式.
(2)若直线y=kx+b(k≠0)与x轴交于点C,x轴上是否存在一点P,使S△APC=4 若存在,请求出点P坐标;若不存在,说明理由.
12.(10分)如图,在平面直角坐标系中,直线y=-nx+12(n≠0)与坐标轴的正半轴相交于A,B两点,与反比例函数y=的图象相交于第一象限内的C,D两点,点C,D是线段AB的三等分点.
(1)用含n的代数式表示点B的坐标;
(2)若n=2,求反比例函数y=的解析式.
13.(10分)如图,在平面直角坐标系中,点M为OA的中点,AB⊥x轴于点B,反比例函数y=(k>0,x>0)的图象经过点M,交AB于点C.
(1)若点A的坐标为(2,6),则k= .点C的坐标为 ;
(2)连接MC,OC,若△OMC的面积为3,求k的值.
14.(10分)如图,经过原点O的直线与反比例函数y=(a>0)的图象交于A、D两点(点A在第一象限),点B、C、E在反比例函数y=(b<0)的图象上,AB∥y轴,AE∥CD∥x轴,五边形ABCDE的面积为56,四边形ABCD的面积为32.求下列各式的值:
(1)a-b; (2).
15.(12分)如图,在平面直角坐标系xOy中,△OA1B1是等边三角形,点B1的坐标是(2,0),反比例函数y=的图象经过点A1.
(1)求反比例函数的解析式.
(2)如图,以B1为顶点作等边三角形B1A2B2,使点B2在x轴上,点A2在反比例函数y=的图象上.若要使点B2在反比例函数y=的图象上,需将△B1A2B2向上平移多少个单位长度
参考答案
一、选择题
1 2 3 4 5 6
C D A D B B
4. D 【解析】∵AC⊥x轴,∴S△AOC=OC·AC=|k|.∵点D是AC的中点,S△AOD=1,∴S△AOC=2S△AOD=2,∴|k|=2,即|k|=4.∵k>0,∴k=4.
5.B 【解析】设点P(m,m+2),∵OP=,∴=,解得m1=2,m2=-4(不合题意舍去),∴点P(2,4),∴4=,解得k=8.
6.B 【解析】如图,过点C作CE⊥x轴于点E,∵四边形ABOC是菱形,AB=2,∠A=60°,∴OC=2,∠COE=60°,∴OE=OC·cos 60°=1,CE=OC·sin 60°=,∴C(-1,),∴k=-,∴反比例函数的解析式为y=-.
二、填空题
7 8 9 10
-1
8.y= 【解析】∵矩形ABCD的边AB与y轴平行,A(1,m),C(3,m+6),∴B(1,m+6),D(3,m),∵B、D在反比例函数图象上,∴1×(m+6)=3m,解得m=3,∴B(1,9),故反比例函数表达式为y=.
9. 【解析】∵S矩形BDOE=|k|=4,k>0,∴k=4,∵AC=1,令x=1,则=y,解得y==4,∴A(1,4),∴OC=4,∵OD=BE=1,∴CD=OC-OD=4-1=3,∴S△ACD=CD·AC=×3×1=.
10.(0,10)或(0,) 【解析】由,得或,∴A(8,4),∵点C在线段AB上,且AC=OC.设点C(c,4),∵OC==,AC=AB-BC=8-c,∴=8-c,解得c=3,∴点C(3,4),∴BC=3,设点P(0,p),当点P为B点上方时,∴OP=p,BP=p-4,∵A(8,4),C(3,4),∴AC=8-3=5,BC=3,∵△POC与△PAC的面积相等,∴×3p=×5(p-4),解得p=10,∴P(0,10).当点P为B点下方时,∴OP=|p|,BP=4-p,∴×3|p|=×5(4-p),解得p=,∴P(0,).综上,点P的坐标为(0,10)或(0,).
三、解答题
11.解:(1)把点A(1,2)代入y=,得2=,∴m=2,
∴反比例函数的解析式为y=;(2分)
把B(a,-1)代入y=,得a=-2,∴B(-2,-1),
把点A(1,2),B(-2,-1)代入y=kx+b,得,解得.
∴一次函数的解析式为y=x+1;(4分)
(2)当y=0时,0=x+1,解得x=-1,∴C(-1,0),
设P(x,0),∴S△APC=×|x+1|×2=4,∴x=3或x=-5,
∴P(3,0)或(-5,0).(8分)
12.解:(1)∵直线y=-nx+12(n≠0)与坐标轴的正半轴相交于A,B两点,
∴令y=0,则0=-nx+12,∴x=,∴B(,0); (4分)
(2)作DE⊥x轴于点E,n=2,则y=-2x+12,
∴B(6,0),∴OB=6,
∵点C,D是AB的三等分点,∴OE=4,
把x=4代入y=-2x+12,得y=4,∴D(4,4),
∵D在反比例函数y=的图象上,∴k=4×4=16,
∴反比例函数解析式为y=.(10分)
13.解:(1)过点M作MD⊥x轴于点D,如图,
∵点A的坐标为(2,6),∴OB=2,AB=6.
∵AB⊥OB,MD⊥OB,∴MD∥AB.
∵点M为OA的中点,∴OD=OB=1,MD=AB=3.
∴M(1,3).∴k=1×3=3.当x=2时,y=.∴C(2,).
故答案为3;(2,).(5分)
(2)设M(a,b),则OD=a,MD=b,k=ab.
由(1)知:OB=2OD=2a,AB=2MD=2b.∴A(2a,2b).
∵AB⊥OB,∴C点的横坐标为2a,
∴C(2a,).
∴BC=.∴AC=AB-BC=2b-.
∵S△OMC=3,OM=AM,∴S△AOC=2×3=6.
∴AC×OB=6.∴×2a×(2b-)=6.∴2ab-k=6.
即2k-k=6.解得k=4.(10分)
14.解:(1)如图,连接EC,AC,设A(m,),
∵AE∥DC∥x轴,∴可得E(,),
∵五边形ABCDE的面积为56,四边形ABCD的面积为32,
∴S△AED=24,即·(m-)·=24,∴a-b=24;(5分)
(2)由反比例函数图象的对称性得,AO=DO,EO=OC,
∴四边形AEDC为平行四边形,∴S△ABC=56-2×24=8,C(-,-),
∵AB∥y轴,∴B(m,),∴·(-)·(m+)=8,即(a-b)·(1+)=16,
∵a-b=24,∴1+=,∴=-.(10分)
15.解:(1)如图1,过点A1作A1H⊥x轴于点H.
∵△OA1B1是等边三角形,点B1的坐标是(2,0),∴OA1=OB1=2,OH=1,
∴A1H===,∴A1(1,).
∵点A1在反比例函数y=的图象上,∴k=.
∴反比例函数的解析式为y=;(5分)
(2)如图2,过点A2作A2G⊥x轴于点G,设B1G=a,则A2G=a,∴A2(2+a,a).
∵点A2在反比例函数y=的图象上,∴a=,
解得a1=-1,a2=--1(不合题意,舍去),∴a=-1,
∴△B1A2B2的边长是2(-1),
∴B2(2,0),
∴把x=2代入y=,得y==,
∴(2,)在反比例函数y=的图象上,
∴若要使点B2在反比例函数y=的图象上,需将△B1A2B2向上平移个单位长度.(12分)
