专项训练卷(四)解直角三角形的实际应用 (含答案)人教版九年级数学下册
文档属性
| 名称 | 专项训练卷(四)解直角三角形的实际应用 (含答案)人教版九年级数学下册 |  | |
| 格式 | docx | ||
| 文件大小 | 236.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-03-30 08:10:41 | ||
图片预览

文档简介
专项训练卷(四)
时间:60分钟 满分:100分 范围:解直角三角形的实际应用
一、选择题(本题共6小题,每小题5分,共30分)
1.如图,某厂房人字架屋顶的上弦AB=AC=10米,∠B=α,则该屋顶的跨度BC为 ( )
A.10sin α米 B.10cos α米 C.20sin α米 D.20cos α米
2.如图,为了测量山坡护坡石坝(图中阴影部分)的坡度(坡面的铅直高度与水平宽度的比称为坡度),把一根长5 m的竹竿AC斜靠在石坝旁,量出杆长1 m处的D点离地面高度DE=0.6 m,又量得杆底与坝脚的距离AB=3 m,则石坝的坡度为 ( )
A. B.3 C. D.4
3.如图,为安全起见,萌萌拟加长滑梯,将其倾斜角由45°降至30°.已知滑梯AB的长为3 m,点D、B、C在同一水平地面上,那么加长后的滑梯AD的长是 ( )
A.2 m B.2 m C.3 m D.3 m
4.如图,一块矩形木板ABCD斜靠在墙边,OC⊥OB,点A,B,C,D,O在同一平面内,已知AB=2,AD=8,∠BCO=x,则点A到OC的距离等于 ( )
A.2sin x+8sin x B.2cos x+8cos x C.2sin x+8cos x D.2cos x+8sin x
5.小阳发现电线杆AB的影子落在土坡的坡面CD和地面BC上,量得CD=8米,BC=20米,CD与地面成30°角,且此时测得1米杆的影长为2米,则电线杆的高度为 ( )
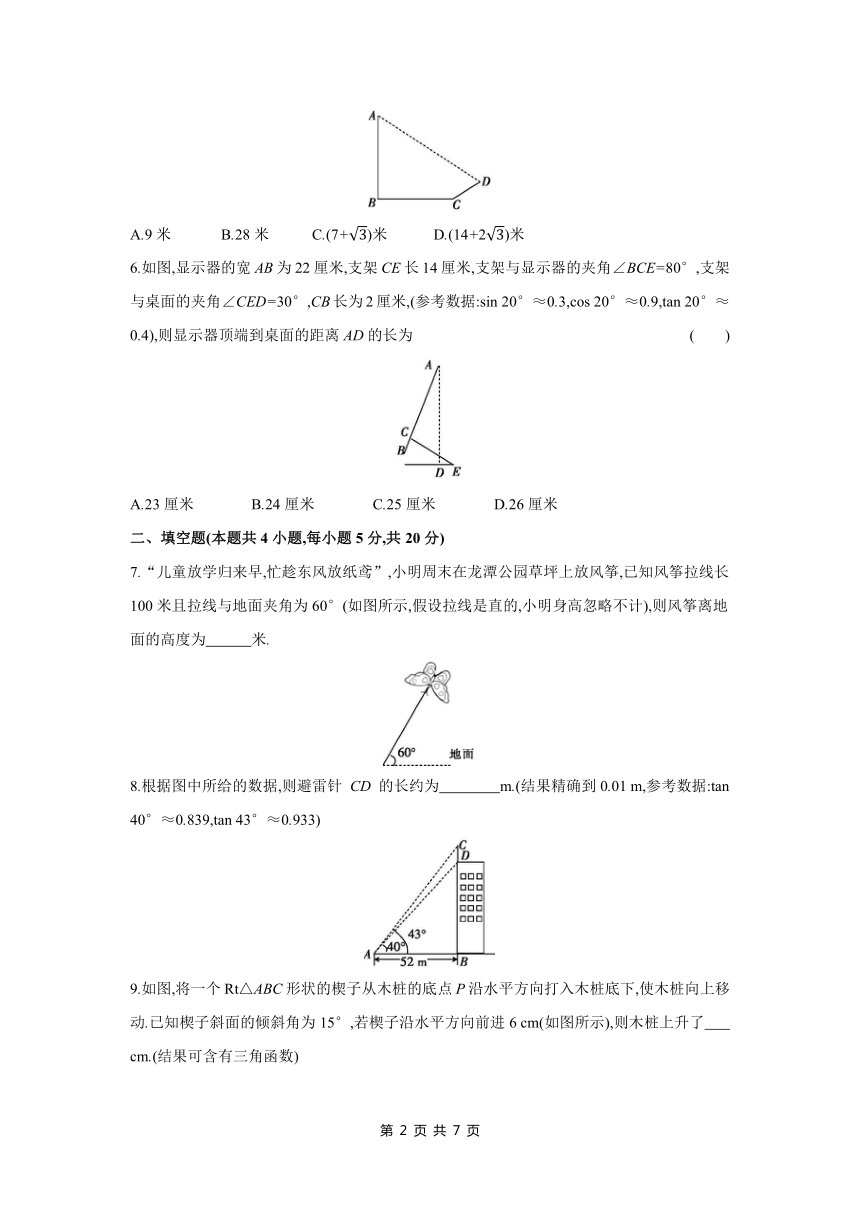
A.9米 B.28米 C.(7+)米 D.(14+2)米
6.如图,显示器的宽AB为22厘米,支架CE长14厘米,支架与显示器的夹角∠BCE=80°,支架与桌面的夹角∠CED=30°,CB长为2厘米,(参考数据:sin 20°≈0.3,cos 20°≈0.9,tan 20°≈0.4),则显示器顶端到桌面的距离AD的长为 ( )
A.23厘米 B.24厘米 C.25厘米 D.26厘米
二、填空题(本题共4小题,每小题5分,共20分)
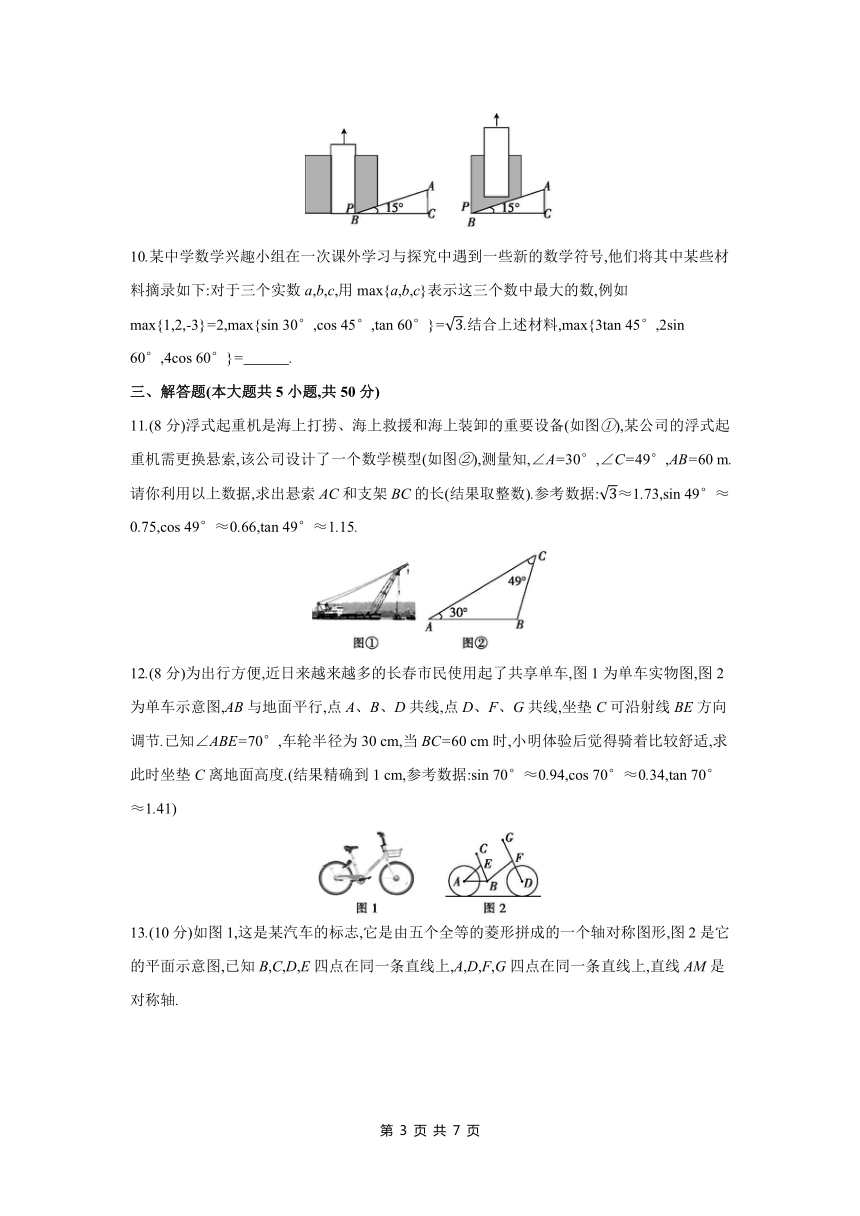
7.“儿童放学归来早,忙趁东风放纸鸢”,小明周末在龙潭公园草坪上放风筝,已知风筝拉线长100米且拉线与地面夹角为60°(如图所示,假设拉线是直的,小明身高忽略不计),则风筝离地面的高度为 米.
8.根据图中所给的数据,则避雷针 CD 的长约为 m.(结果精确到0.01 m,参考数据:tan 40°≈0.839,tan 43°≈0.933)
9.如图,将一个Rt△ABC形状的楔子从木桩的底点P沿水平方向打入木桩底下,使木桩向上移动.已知楔子斜面的倾斜角为15°,若楔子沿水平方向前进6 cm(如图所示),则木桩上升了 cm.(结果可含有三角函数)
10.某中学数学兴趣小组在一次课外学习与探究中遇到一些新的数学符号,他们将其中某些材料摘录如下:对于三个实数a,b,c,用max{a,b,c}表示这三个数中最大的数,例如max{1,2,-3}=2,max{sin 30°,cos 45°,tan 60°}=.结合上述材料,max{3tan 45°,2sin 60°,4cos 60°}= .
三、解答题(本大题共5小题,共50分)
11.(8分)浮式起重机是海上打捞、海上救援和海上装卸的重要设备(如图①),某公司的浮式起重机需更换悬索,该公司设计了一个数学模型(如图②),测量知,∠A=30°,∠C=49°,AB=60 m.请你利用以上数据,求出悬索AC和支架BC的长(结果取整数).参考数据:≈1.73,sin 49°≈0.75,cos 49°≈0.66,tan 49°≈1.15.
12.(8分)为出行方便,近日来越来越多的长春市民使用起了共享单车,图1为单车实物图,图2为单车示意图,AB与地面平行,点A、B、D共线,点D、F、G共线,坐垫C可沿射线BE方向调节.已知∠ABE=70°,车轮半径为30 cm,当BC=60 cm时,小明体验后觉得骑着比较舒适,求此时坐垫C离地面高度.(结果精确到1 cm,参考数据:sin 70°≈0.94,cos 70°≈0.34,tan 70°≈1.41)
13.(10分)如图1,这是某汽车的标志,它是由五个全等的菱形拼成的一个轴对称图形,图2是它的平面示意图,已知B,C,D,E四点在同一条直线上,A,D,F,G四点在同一条直线上,直线AM是对称轴.
(1)求证:∠CAD=60°.
(2)连接AH,若菱形的边长为4 cm,求线段AH的长.
14.(12分)图1是光伏发电场景,其示意图如图2,EF为吸热塔,在地平线EG上的点B,B'处各安装定日镜(介绍见图3).绕各中心点(A,A')旋转镜面,使过中心点的太阳光线经镜面反射后到达吸热器点F处.已知AB=A'B'=1 m,EB=8 m,EB'=8 m,在点A处观测点F的仰角为45°.
(1)求点F的高EF;
(2)设∠DAB=α,∠D'A'B'=β,直接写出α与β的数量关系式.
15.(12分)有一只拉杆式旅行箱(图1),其侧面示意图如图2所示,已知箱体长AB=50 cm,拉杆BC的伸长距离最大时可达30 cm,点A、B、C在同一条直线上,在箱体底端装有圆形的滚轮☉A,☉A与水平地面切于点D,在拉杆伸长至最大的情况下,当点B距离水平地面36 cm时,点C到水平面的距离CE为54 cm,设AF∥MN.
(1)求☉A的半径长;
(2)当某人的手自然下垂在C端拉旅行箱时,CE为66 cm,∠CAF=53°,求此时拉杆BC的伸长距离.(参考数据:sin 53°≈0.80,cos 53°≈0.60,tan 53°≈1.33,结果精确到1 cm)
参考答案
一、选择题
1 2 3 4 5 6
D B C D D C
4.D 【解析】作AE⊥OC于点E,作AF⊥OB于点F,∵四边形ABCD是矩形,∴∠ABC=90°,∵∠ABC=∠AEC,∠BCO=x,∴∠EAB=x,∴∠FBA=x,∵AB=2,AD=8,∴FO=FB+BO=2cos x+8sin x.
5.D 【解析】延长AD交BC的延长线于F点,作DE⊥CF于E点.DE=8sin 30°=4;CE=8cos 30°=4;∴EF=2DE=8,∴BF=BC+CE+EF=20+4+8=28+4,∵测得1米杆的影长为2米.∴电线杆AB的长度是(28+4)=(14+2)米.
6.C 【解析】过点C作CG⊥DE于点G,作CF⊥AD于点F,如图所示,则AD=AF+DF=AF+CG,∵∠CED=30°,支架CE长14厘米,∴CG=CE=7厘米,∵AB为22厘米,CB长为2厘米,∴AC=20厘米,∵∠BCE=80°,∴∠ACE=180°-80°=100°,∵CF⊥AD,∴CF∥DE,∴∠ECF=∠CED=30°,∴∠ACF=70°,∴∠A=20°,在Rt△ACF中,AF=AC·cos∠A=AC·cos 20°≈20×0.9=18(厘米),∴AD=AF+DF=AF+CG=18+7=25(厘米).
二、填空题
7 8 9 10
50 4.89 6tan 15° 3
8.4.89 【解析】∵tan∠BAC=,tan∠BAD=,∴BC=ABtan∠BAC,BD=ABtan∠BAD,则CD=BC-BD=ABtan∠BAC-ABtan∠BAD=AB(tan 43°-tan 40°)≈52(0.933-0.839)≈4.89.
9.6tan 15° 【解析】设木桩上升了x cm,则tan 15°=,解得x=6tan 15°,则木桩上升了6tan 15° cm.
10.3 【解析】∵3tan 45°=3×1=3,2sin 60°=2×=,4cos 60°=4×=2,∴3>2>,∴max{3tan 45°,2sin 60°,4cos 60°}=3.
三、解答题
11.解:过点B作BD⊥AC于点D,
∵∠A=30°,AB=60,∴BD=AB=30(m),
∴AD=BD=30(m).(3分)
在Rt△CBD中,tan 49°=,sin 49°=,
∴CD≈26 m,BC≈40 m,∴AC=AD+CD≈78 m.(8分)
12.解:作CH⊥AB于H,作AP⊥地面于P,
由题知,AP=30 cm,BC=60 cm,∠ABE=70°,(4分)
∴CH=BC·sin 70°≈60×0.94=56.4(cm),
∴坐垫C离地面高度约为56.4+30≈86(cm).(8分)
13.解:(1)证明:∵四边形ADMC是菱形,∴AC=AD,∠MDC=∠ADC.
又∵菱形ACMD与菱形EDFN全等,∴∠MDA=∠DFN.
在菱形EDFN中,∠DFN+∠FDE=180°,∵∠ADC=∠FDE,
∴∠FDE+∠MDA=180°,
∴3∠ADC=180°,∴∠ADC=60°,
∴△ACD是等边三角形,∴∠CAD=60°.(5分)
(2)AH=4 cm.(10分)
14.解:(1)过点A作AG⊥EF,垂足为G.
∵∠ABE=∠BEG=∠EGA=90°,
∴四边形ABEG是矩形,∴EG=AB=1 m,AG=EB=8 m,
∵∠FAG=45°,∴FG=AG=EB=8 m,∴EF=FG+EG=9(m).
答:EF为9 m.(4分)
(2)α与β的数量关系式为α-β=7.5°.理由如下:
∵∠A'B'E=∠B'EG=∠EGA'=90°,∴四边形A'B'EG是矩形,
∴EG=A'B'=1 m,A'G=EB'=8,∴tan∠A'FG===,
∴∠A'FG=60°,∠FA'G=30°,
根据光的反射原理,不妨设∠FAN=2m,∠FA'M=2n,∵光线是平行的,
∴AN∥A'M,∴∠GAN=∠GA'M,
∴45°+2m=30°+2n,解得n-m=7.5°,
由图可得∠DAB=α=45°+m,∠D'A'B'=β=30°+n,
∴α-β=n-m=7.5°,故α-β=7.5°.(12分)
15.解:(1)☉A的半径长为6 cm;(6分)
(2)在Rt△ACG中,CG=66-6=60(cm),
∵sin∠CAF=,∴AC=≈=75(cm),
∴BC=AC-AB=75-50=25(cm),
∴此时拉杆BC的伸长距离约为25 cm.(12分)
时间:60分钟 满分:100分 范围:解直角三角形的实际应用
一、选择题(本题共6小题,每小题5分,共30分)
1.如图,某厂房人字架屋顶的上弦AB=AC=10米,∠B=α,则该屋顶的跨度BC为 ( )
A.10sin α米 B.10cos α米 C.20sin α米 D.20cos α米
2.如图,为了测量山坡护坡石坝(图中阴影部分)的坡度(坡面的铅直高度与水平宽度的比称为坡度),把一根长5 m的竹竿AC斜靠在石坝旁,量出杆长1 m处的D点离地面高度DE=0.6 m,又量得杆底与坝脚的距离AB=3 m,则石坝的坡度为 ( )
A. B.3 C. D.4
3.如图,为安全起见,萌萌拟加长滑梯,将其倾斜角由45°降至30°.已知滑梯AB的长为3 m,点D、B、C在同一水平地面上,那么加长后的滑梯AD的长是 ( )
A.2 m B.2 m C.3 m D.3 m
4.如图,一块矩形木板ABCD斜靠在墙边,OC⊥OB,点A,B,C,D,O在同一平面内,已知AB=2,AD=8,∠BCO=x,则点A到OC的距离等于 ( )
A.2sin x+8sin x B.2cos x+8cos x C.2sin x+8cos x D.2cos x+8sin x
5.小阳发现电线杆AB的影子落在土坡的坡面CD和地面BC上,量得CD=8米,BC=20米,CD与地面成30°角,且此时测得1米杆的影长为2米,则电线杆的高度为 ( )
A.9米 B.28米 C.(7+)米 D.(14+2)米
6.如图,显示器的宽AB为22厘米,支架CE长14厘米,支架与显示器的夹角∠BCE=80°,支架与桌面的夹角∠CED=30°,CB长为2厘米,(参考数据:sin 20°≈0.3,cos 20°≈0.9,tan 20°≈0.4),则显示器顶端到桌面的距离AD的长为 ( )
A.23厘米 B.24厘米 C.25厘米 D.26厘米
二、填空题(本题共4小题,每小题5分,共20分)
7.“儿童放学归来早,忙趁东风放纸鸢”,小明周末在龙潭公园草坪上放风筝,已知风筝拉线长100米且拉线与地面夹角为60°(如图所示,假设拉线是直的,小明身高忽略不计),则风筝离地面的高度为 米.
8.根据图中所给的数据,则避雷针 CD 的长约为 m.(结果精确到0.01 m,参考数据:tan 40°≈0.839,tan 43°≈0.933)
9.如图,将一个Rt△ABC形状的楔子从木桩的底点P沿水平方向打入木桩底下,使木桩向上移动.已知楔子斜面的倾斜角为15°,若楔子沿水平方向前进6 cm(如图所示),则木桩上升了 cm.(结果可含有三角函数)
10.某中学数学兴趣小组在一次课外学习与探究中遇到一些新的数学符号,他们将其中某些材料摘录如下:对于三个实数a,b,c,用max{a,b,c}表示这三个数中最大的数,例如max{1,2,-3}=2,max{sin 30°,cos 45°,tan 60°}=.结合上述材料,max{3tan 45°,2sin 60°,4cos 60°}= .
三、解答题(本大题共5小题,共50分)
11.(8分)浮式起重机是海上打捞、海上救援和海上装卸的重要设备(如图①),某公司的浮式起重机需更换悬索,该公司设计了一个数学模型(如图②),测量知,∠A=30°,∠C=49°,AB=60 m.请你利用以上数据,求出悬索AC和支架BC的长(结果取整数).参考数据:≈1.73,sin 49°≈0.75,cos 49°≈0.66,tan 49°≈1.15.
12.(8分)为出行方便,近日来越来越多的长春市民使用起了共享单车,图1为单车实物图,图2为单车示意图,AB与地面平行,点A、B、D共线,点D、F、G共线,坐垫C可沿射线BE方向调节.已知∠ABE=70°,车轮半径为30 cm,当BC=60 cm时,小明体验后觉得骑着比较舒适,求此时坐垫C离地面高度.(结果精确到1 cm,参考数据:sin 70°≈0.94,cos 70°≈0.34,tan 70°≈1.41)
13.(10分)如图1,这是某汽车的标志,它是由五个全等的菱形拼成的一个轴对称图形,图2是它的平面示意图,已知B,C,D,E四点在同一条直线上,A,D,F,G四点在同一条直线上,直线AM是对称轴.
(1)求证:∠CAD=60°.
(2)连接AH,若菱形的边长为4 cm,求线段AH的长.
14.(12分)图1是光伏发电场景,其示意图如图2,EF为吸热塔,在地平线EG上的点B,B'处各安装定日镜(介绍见图3).绕各中心点(A,A')旋转镜面,使过中心点的太阳光线经镜面反射后到达吸热器点F处.已知AB=A'B'=1 m,EB=8 m,EB'=8 m,在点A处观测点F的仰角为45°.
(1)求点F的高EF;
(2)设∠DAB=α,∠D'A'B'=β,直接写出α与β的数量关系式.
15.(12分)有一只拉杆式旅行箱(图1),其侧面示意图如图2所示,已知箱体长AB=50 cm,拉杆BC的伸长距离最大时可达30 cm,点A、B、C在同一条直线上,在箱体底端装有圆形的滚轮☉A,☉A与水平地面切于点D,在拉杆伸长至最大的情况下,当点B距离水平地面36 cm时,点C到水平面的距离CE为54 cm,设AF∥MN.
(1)求☉A的半径长;
(2)当某人的手自然下垂在C端拉旅行箱时,CE为66 cm,∠CAF=53°,求此时拉杆BC的伸长距离.(参考数据:sin 53°≈0.80,cos 53°≈0.60,tan 53°≈1.33,结果精确到1 cm)
参考答案
一、选择题
1 2 3 4 5 6
D B C D D C
4.D 【解析】作AE⊥OC于点E,作AF⊥OB于点F,∵四边形ABCD是矩形,∴∠ABC=90°,∵∠ABC=∠AEC,∠BCO=x,∴∠EAB=x,∴∠FBA=x,∵AB=2,AD=8,∴FO=FB+BO=2cos x+8sin x.
5.D 【解析】延长AD交BC的延长线于F点,作DE⊥CF于E点.DE=8sin 30°=4;CE=8cos 30°=4;∴EF=2DE=8,∴BF=BC+CE+EF=20+4+8=28+4,∵测得1米杆的影长为2米.∴电线杆AB的长度是(28+4)=(14+2)米.
6.C 【解析】过点C作CG⊥DE于点G,作CF⊥AD于点F,如图所示,则AD=AF+DF=AF+CG,∵∠CED=30°,支架CE长14厘米,∴CG=CE=7厘米,∵AB为22厘米,CB长为2厘米,∴AC=20厘米,∵∠BCE=80°,∴∠ACE=180°-80°=100°,∵CF⊥AD,∴CF∥DE,∴∠ECF=∠CED=30°,∴∠ACF=70°,∴∠A=20°,在Rt△ACF中,AF=AC·cos∠A=AC·cos 20°≈20×0.9=18(厘米),∴AD=AF+DF=AF+CG=18+7=25(厘米).
二、填空题
7 8 9 10
50 4.89 6tan 15° 3
8.4.89 【解析】∵tan∠BAC=,tan∠BAD=,∴BC=ABtan∠BAC,BD=ABtan∠BAD,则CD=BC-BD=ABtan∠BAC-ABtan∠BAD=AB(tan 43°-tan 40°)≈52(0.933-0.839)≈4.89.
9.6tan 15° 【解析】设木桩上升了x cm,则tan 15°=,解得x=6tan 15°,则木桩上升了6tan 15° cm.
10.3 【解析】∵3tan 45°=3×1=3,2sin 60°=2×=,4cos 60°=4×=2,∴3>2>,∴max{3tan 45°,2sin 60°,4cos 60°}=3.
三、解答题
11.解:过点B作BD⊥AC于点D,
∵∠A=30°,AB=60,∴BD=AB=30(m),
∴AD=BD=30(m).(3分)
在Rt△CBD中,tan 49°=,sin 49°=,
∴CD≈26 m,BC≈40 m,∴AC=AD+CD≈78 m.(8分)
12.解:作CH⊥AB于H,作AP⊥地面于P,
由题知,AP=30 cm,BC=60 cm,∠ABE=70°,(4分)
∴CH=BC·sin 70°≈60×0.94=56.4(cm),
∴坐垫C离地面高度约为56.4+30≈86(cm).(8分)
13.解:(1)证明:∵四边形ADMC是菱形,∴AC=AD,∠MDC=∠ADC.
又∵菱形ACMD与菱形EDFN全等,∴∠MDA=∠DFN.
在菱形EDFN中,∠DFN+∠FDE=180°,∵∠ADC=∠FDE,
∴∠FDE+∠MDA=180°,
∴3∠ADC=180°,∴∠ADC=60°,
∴△ACD是等边三角形,∴∠CAD=60°.(5分)
(2)AH=4 cm.(10分)
14.解:(1)过点A作AG⊥EF,垂足为G.
∵∠ABE=∠BEG=∠EGA=90°,
∴四边形ABEG是矩形,∴EG=AB=1 m,AG=EB=8 m,
∵∠FAG=45°,∴FG=AG=EB=8 m,∴EF=FG+EG=9(m).
答:EF为9 m.(4分)
(2)α与β的数量关系式为α-β=7.5°.理由如下:
∵∠A'B'E=∠B'EG=∠EGA'=90°,∴四边形A'B'EG是矩形,
∴EG=A'B'=1 m,A'G=EB'=8,∴tan∠A'FG===,
∴∠A'FG=60°,∠FA'G=30°,
根据光的反射原理,不妨设∠FAN=2m,∠FA'M=2n,∵光线是平行的,
∴AN∥A'M,∴∠GAN=∠GA'M,
∴45°+2m=30°+2n,解得n-m=7.5°,
由图可得∠DAB=α=45°+m,∠D'A'B'=β=30°+n,
∴α-β=n-m=7.5°,故α-β=7.5°.(12分)
15.解:(1)☉A的半径长为6 cm;(6分)
(2)在Rt△ACG中,CG=66-6=60(cm),
∵sin∠CAF=,∴AC=≈=75(cm),
∴BC=AC-AB=75-50=25(cm),
∴此时拉杆BC的伸长距离约为25 cm.(12分)
