期中真题专项复习02 填空题(含答案)--2024-2025学年七年级数学下册(湘教版2024)
文档属性
| 名称 | 期中真题专项复习02 填空题(含答案)--2024-2025学年七年级数学下册(湘教版2024) |  | |
| 格式 | docx | ||
| 文件大小 | 300.5KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-03-30 05:55:40 | ||
图片预览



文档简介
2024-2025学年七年级数学下册(湘教版2024)
期中真题专项复习02 填空题
一、填空题
1.(2024七下·赫山期中)关于的多项式乘多项式,若结果中不含有的一次项,则的值为 .
2.(2024七下·长沙期中) 已知的整数部分是1,则小数部分是;若的小数部分为a,则 .
3.(2024七下·赫山期中) .
4.(2024七下·衡阳期中)关于的不等式组有解且每一个的值均不在的范围中,则的取值范围是 .
5.(2024七下·祁阳期中)我们知道,同底数幂的乘法法则为,类似地,我们规定关于任意正整数的一种新运算:,请根据这种新运算填空,若,那么 .
6.(2024七下·江山期中)如图,在一块长为am,宽为bm的长方形草地上,有一条弯曲的小路,小路的左边线向右平移1m就是它的右边线.则这块草地的绿地面积是 m2.
7.(2024七下·衡东期中)六一儿童节到了,要把一些苹果分给几个小朋友,如果每人分3个,那么剩8个;如果每人分5个,那么最后一个小朋友就分不到3个,则共有 个小朋友.
8.(2024七下·自贡期中)如图,在长方形地块内修筑同样宽的两条“相交”的道路,余下部分作绿化,当道路宽为2米时,绿化的面积为 平方米.
9.(2024七下·武冈期中)已知,计算: .
10.(2024七下·邵东期中)若与的乘积不含的一次项,则的值为 .
11.(2024七下·单县期中)计算 .
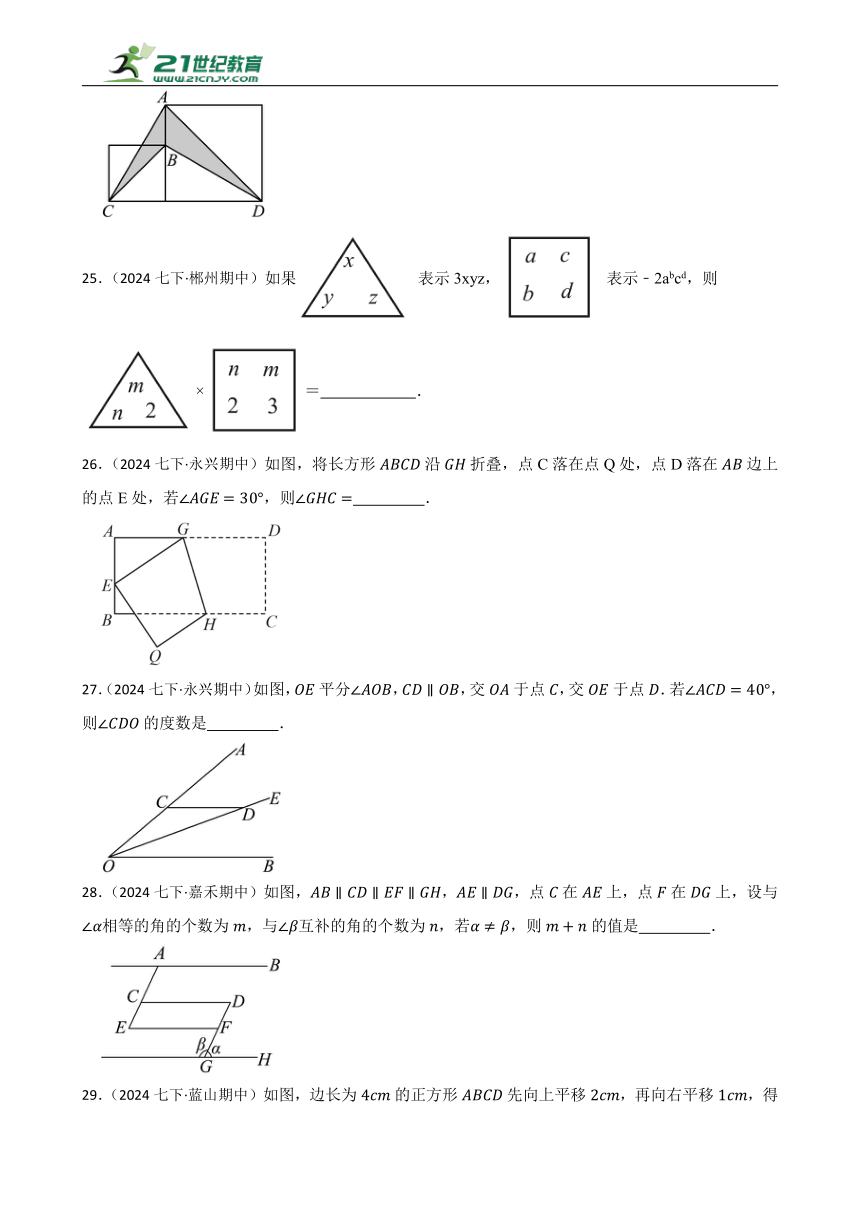
12.(2024七下·安化期中)如图,中,,把沿方向平移到的位置,若,则图中阴影部分的面积为 .
13.(2024七下·安化期中)已知代数式化简后,不含项,则a的值为 .
14.(2023七下·长沙期中)设为正整数,且,则的值为 .
15.(2024七下·永州期中)已知多项式因式分解后有一个因式为,则的值为 .
16.(2024七下·长沙期中)如图,在中,,于点D,,若点E在边(不与点A,B重合)移动,则线段最短为
17.(2024七下·长沙期中)m、n为两个连续的整数,,则m+n= .
18.(2024七下·郴州期中)在的展开式中,x的一次项系数是3,则m的值是 .
19.(2024七下·娄底期中)计算: ;
20.(2024七下·安化期中)如图,已知,,,则 度.
21.(2024七下·岳阳期中)光的速度约为,太阳光照到地球上要,那么太阳与地球的距离为 (用科学记数法表示).
22.(2024七下·永定期中)计算: .
23.(2024七下·祁阳期中)已知,则 .
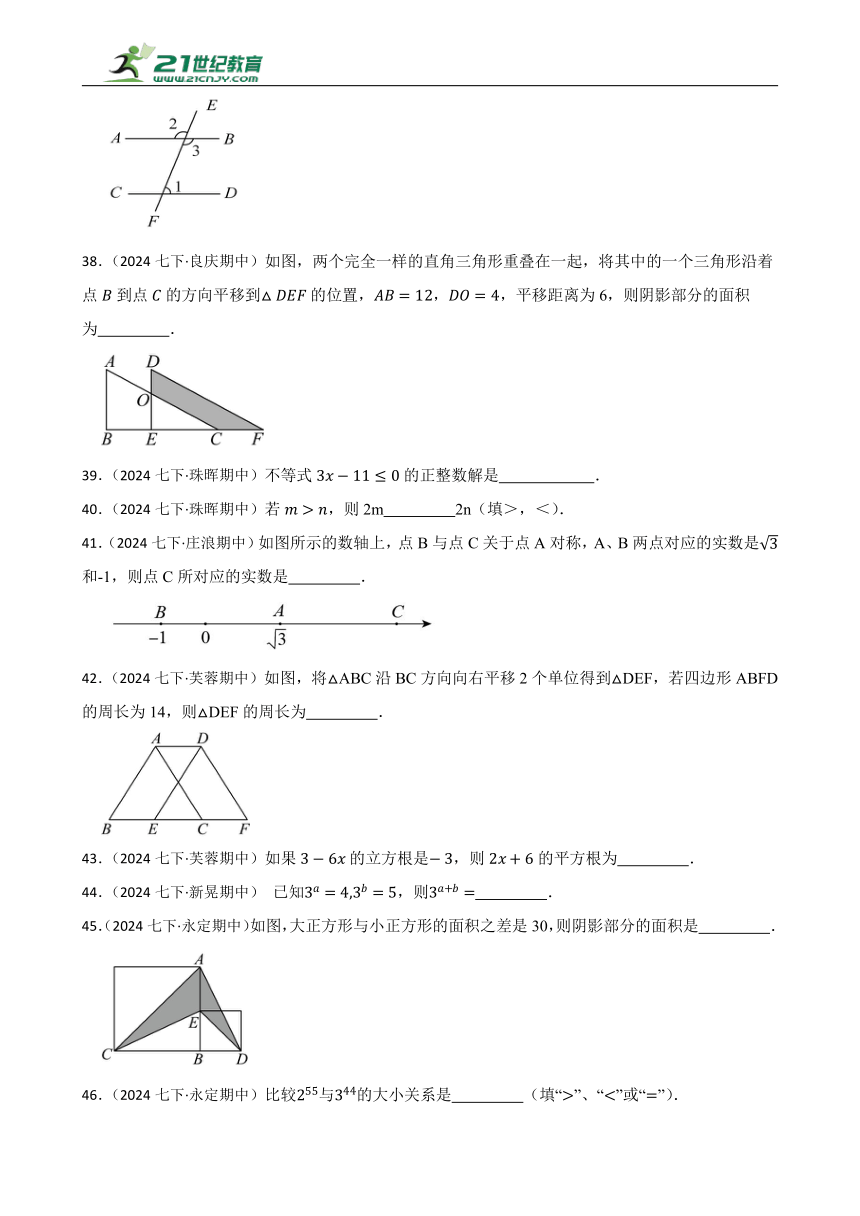
24.(2024七下·郴州期中)如图,若大正方形与小正方形的面积之差为28,则图中阴影部分的面积是 .
25.(2024七下·郴州期中)如果 表示3xyz, 表示﹣2abcd,则×= .
26.(2024七下·永兴期中)如图,将长方形沿折叠,点C落在点Q处,点D落在边上的点E处,若,则 .
27.(2024七下·永兴期中)如图,平分,,交于点,交于点.若,则的度数是 .
28.(2024七下·嘉禾期中)如图,,,点在上,点在上,设与相等的角的个数为,与互补的角的个数为,若,则的值是 .
29.(2024七下·蓝山期中)如图,边长为的正方形先向上平移,再向右平移,得到正方形,此时阴影部分的面积为 .
30.(2024七下·永州期中)我国宋代数学家杨辉所著《详解九章算法》中记载了用如图所示的三角形解释了二项和的乘方展开式中的系数规律,我们把这种数字三角形叫做“杨辉三角”.请你利用杨辉三角,计算(a+b)6的展开式中,从左起第四项是 .
31.(2024七下·新田期中)用完全平方公式计算 .
32.(2024七下·衡阳期中)下面是一个被墨水污染过的方程:,答案显示方程的解是负数,若被墨水遮盖的是一个常数,则这个常数的取值范围是 .
33.(2024七下·新田期中)已知实数满足,则 .
34.(2024七下·新田期中)已知一个正方形的边长是,则它的面积是 (用科学记数法表示)。
35.(2024七下·新田期中)计算: .
36.(2024七下·邵东期中)如图,直线,点C在上.若,的面积为27,的面积为18,则 .
37.(2024七下·邵东期中)如图,AB∥CD,EF分别交AB、CD于点E、F,∠1=70°,则∠2= .
38.(2024七下·良庆期中)如图,两个完全一样的直角三角形重叠在一起,将其中的一个三角形沿着点到点的方向平移到的位置,,,平移距离为6,则阴影部分的面积为 .
39.(2024七下·珠晖期中)不等式的正整数解是 .
40.(2024七下·珠晖期中)若,则2m 2n(填>,<).
41.(2024七下·庄浪期中)如图所示的数轴上,点B与点C关于点A对称,A、B两点对应的实数是和-1,则点C所对应的实数是 .
42.(2024七下·芙蓉期中)如图,将ABC沿BC方向向右平移2个单位得到DEF,若四边形ABFD的周长为14,则DEF的周长为 .
43.(2024七下·芙蓉期中)如果的立方根是,则的平方根为 .
44.(2024七下·新晃期中) 已知,则 .
45.(2024七下·永定期中)如图,大正方形与小正方形的面积之差是30,则阴影部分的面积是 .
46.(2024七下·永定期中)比较与的大小关系是 (填“”、“”或“”).
47.(2024七下·永定期中)若,,则 .
48.(2024七下·通道期中)我们知道,同底数幂的乘法法则为(其中,,为正整数),类似的,我们规定关于任意正整数,的一种新运算:,请根据这种新运算填空:
(1)若,则 ;
(2)若,那么 .(用含和的代数式表示,其中为正整数).
49.(2024七下·通道期中)计算: .
50.(2024七下·临武期中)如图,若大正方形与小正方形的面积之差为20,则阴影部分的面积是 .
答案解析部分
1.
2.
解:∵,
∴.
∴.
故答案为:.
估算出的范围,再得到a即可.
3.
4.
5.
解:由h(1)代入新运算定义中,
则有,
,
,
......
.....
,
∴.
故填:.
通过由已知条件代入新运算规则中可先计算,同时在该基础上发现一般性规律,结合同底数幂运算法则即可得出结果.
6.b(a-1)
7.6
8.540
9.5
10.3
11.
12.9
13.
14.7
∵,
∴,
∴n的值为7,
故答案为:7.
利用估算无理数大小的方法求解即可。
15.
16.6
17.7
18.4
19.
20.80
21.1.5×108
解:地球与太阳的距离:.
故答案为:1.5×108.
科学记数法的表示形式为a×10n的形式,其中1≤|a|<10,n为整数.确定n的值时,要看把原数变成a时,小数点移动了多少位,n的绝对值与小数点移动的位数相同.当原数绝对值>1时,n是正数;当原数的绝对值<1时,n是负数.
22.
,
故答案为:.
利用积的乘方和幂的乘方的计算方法逐项分析判断即可.
23.2
解:由,
∴,
解得:x-y=2,
故填:2.
由题干条件联想平方差公式变形可直接联系条件与问题得出结果.
24.14
25.-12m4n3
26.
27.
28.
29.6
解: 边长为的正方形先向上平移,
平移后的阴影部分的宽为2cm,
再向右平移,得到正方形,
平移后的阴影部分的长为3cm,
此时阴影部分的面积为3×2=6cm2.
故答案为:6.
根据平移的距离求出平移后的阴影部分的长和宽,再用长×宽即可得到阴影部分的面积.
30.20a3b3
31.
解:.
故答案为:.
根据完全平方公式进行计算即可求解.
32.
33.26
解:∵,
∴.
故答案为:26.
根据完全平方公式得出,再代入求出答案即可.
34.
解:∵正方形的边长为,
∴正方形的面积为.
故答案为:.
根据正方形的面积公式进行计算即可.
35.
解:.
故答案为:.
根据积的乘方公式以及幂的乘方公式即可求解.
36.6
37.110°
38.60
根据平移的性质可得:DE=AB=12,BE=CF=6,S△ABC=S△DEF,
∴S梯形ABEO+S△OEC=S梯形DOCF+S△OEC,OE=DE-OD=12-4=8,
∴S梯形ABEO=S梯形DOCF,
∴S阴影=S梯形ABEO=(OE+AB)×BE=×(8+12)×6=60,
故答案为:60.
利用平移的性质求出S梯形ABEO=S梯形DOCF,再利用梯形的面积公式列出算式求解即可.
39.1,2,3
40.>
41.2+1
42.10
43.±4
44.20
解:∵,
∴.
故答案为:20.
根据同底数幂相乘的逆运算把3a+b转化为乘法,再整体代入计算即可.
45.15
设大正方形和小正方形的边长各为a,b,
根据题意可得:a2-b2=30,
∴阴影部分的面积=
=
=
=
=15,
故答案为:15.
设大正方形和小正方形的边长各为a,b,根据题意可得:a2-b2=30,再利用割补法求出阴影部分的面积===15即可.
46.<
∵,,32<81,
∴<,
故答案为:<.
先利用幂的乘方将和化简,再比较大小即可.
47.6
∵,,
∴,
故答案为:6.
利用同底数幂的乘法的计算方法分析求解即可.
48.;
49.
50.10
解:设大正方形的边长为,小正方形的边长为,
由题意和图可知:,,,,
∴
;
故答案为:10.
设大正方形的边长为,小正方形的边长为,先求得,,再将阴影部分的面积转化为用表示的形式,再整体代入求值.
期中真题专项复习02 填空题
一、填空题
1.(2024七下·赫山期中)关于的多项式乘多项式,若结果中不含有的一次项,则的值为 .
2.(2024七下·长沙期中) 已知的整数部分是1,则小数部分是;若的小数部分为a,则 .
3.(2024七下·赫山期中) .
4.(2024七下·衡阳期中)关于的不等式组有解且每一个的值均不在的范围中,则的取值范围是 .
5.(2024七下·祁阳期中)我们知道,同底数幂的乘法法则为,类似地,我们规定关于任意正整数的一种新运算:,请根据这种新运算填空,若,那么 .
6.(2024七下·江山期中)如图,在一块长为am,宽为bm的长方形草地上,有一条弯曲的小路,小路的左边线向右平移1m就是它的右边线.则这块草地的绿地面积是 m2.
7.(2024七下·衡东期中)六一儿童节到了,要把一些苹果分给几个小朋友,如果每人分3个,那么剩8个;如果每人分5个,那么最后一个小朋友就分不到3个,则共有 个小朋友.
8.(2024七下·自贡期中)如图,在长方形地块内修筑同样宽的两条“相交”的道路,余下部分作绿化,当道路宽为2米时,绿化的面积为 平方米.
9.(2024七下·武冈期中)已知,计算: .
10.(2024七下·邵东期中)若与的乘积不含的一次项,则的值为 .
11.(2024七下·单县期中)计算 .
12.(2024七下·安化期中)如图,中,,把沿方向平移到的位置,若,则图中阴影部分的面积为 .
13.(2024七下·安化期中)已知代数式化简后,不含项,则a的值为 .
14.(2023七下·长沙期中)设为正整数,且,则的值为 .
15.(2024七下·永州期中)已知多项式因式分解后有一个因式为,则的值为 .
16.(2024七下·长沙期中)如图,在中,,于点D,,若点E在边(不与点A,B重合)移动,则线段最短为
17.(2024七下·长沙期中)m、n为两个连续的整数,,则m+n= .
18.(2024七下·郴州期中)在的展开式中,x的一次项系数是3,则m的值是 .
19.(2024七下·娄底期中)计算: ;
20.(2024七下·安化期中)如图,已知,,,则 度.
21.(2024七下·岳阳期中)光的速度约为,太阳光照到地球上要,那么太阳与地球的距离为 (用科学记数法表示).
22.(2024七下·永定期中)计算: .
23.(2024七下·祁阳期中)已知,则 .
24.(2024七下·郴州期中)如图,若大正方形与小正方形的面积之差为28,则图中阴影部分的面积是 .
25.(2024七下·郴州期中)如果 表示3xyz, 表示﹣2abcd,则×= .
26.(2024七下·永兴期中)如图,将长方形沿折叠,点C落在点Q处,点D落在边上的点E处,若,则 .
27.(2024七下·永兴期中)如图,平分,,交于点,交于点.若,则的度数是 .
28.(2024七下·嘉禾期中)如图,,,点在上,点在上,设与相等的角的个数为,与互补的角的个数为,若,则的值是 .
29.(2024七下·蓝山期中)如图,边长为的正方形先向上平移,再向右平移,得到正方形,此时阴影部分的面积为 .
30.(2024七下·永州期中)我国宋代数学家杨辉所著《详解九章算法》中记载了用如图所示的三角形解释了二项和的乘方展开式中的系数规律,我们把这种数字三角形叫做“杨辉三角”.请你利用杨辉三角,计算(a+b)6的展开式中,从左起第四项是 .
31.(2024七下·新田期中)用完全平方公式计算 .
32.(2024七下·衡阳期中)下面是一个被墨水污染过的方程:,答案显示方程的解是负数,若被墨水遮盖的是一个常数,则这个常数的取值范围是 .
33.(2024七下·新田期中)已知实数满足,则 .
34.(2024七下·新田期中)已知一个正方形的边长是,则它的面积是 (用科学记数法表示)。
35.(2024七下·新田期中)计算: .
36.(2024七下·邵东期中)如图,直线,点C在上.若,的面积为27,的面积为18,则 .
37.(2024七下·邵东期中)如图,AB∥CD,EF分别交AB、CD于点E、F,∠1=70°,则∠2= .
38.(2024七下·良庆期中)如图,两个完全一样的直角三角形重叠在一起,将其中的一个三角形沿着点到点的方向平移到的位置,,,平移距离为6,则阴影部分的面积为 .
39.(2024七下·珠晖期中)不等式的正整数解是 .
40.(2024七下·珠晖期中)若,则2m 2n(填>,<).
41.(2024七下·庄浪期中)如图所示的数轴上,点B与点C关于点A对称,A、B两点对应的实数是和-1,则点C所对应的实数是 .
42.(2024七下·芙蓉期中)如图,将ABC沿BC方向向右平移2个单位得到DEF,若四边形ABFD的周长为14,则DEF的周长为 .
43.(2024七下·芙蓉期中)如果的立方根是,则的平方根为 .
44.(2024七下·新晃期中) 已知,则 .
45.(2024七下·永定期中)如图,大正方形与小正方形的面积之差是30,则阴影部分的面积是 .
46.(2024七下·永定期中)比较与的大小关系是 (填“”、“”或“”).
47.(2024七下·永定期中)若,,则 .
48.(2024七下·通道期中)我们知道,同底数幂的乘法法则为(其中,,为正整数),类似的,我们规定关于任意正整数,的一种新运算:,请根据这种新运算填空:
(1)若,则 ;
(2)若,那么 .(用含和的代数式表示,其中为正整数).
49.(2024七下·通道期中)计算: .
50.(2024七下·临武期中)如图,若大正方形与小正方形的面积之差为20,则阴影部分的面积是 .
答案解析部分
1.
2.
解:∵,
∴.
∴.
故答案为:.
估算出的范围,再得到a即可.
3.
4.
5.
解:由h(1)代入新运算定义中,
则有,
,
,
......
.....
,
∴.
故填:.
通过由已知条件代入新运算规则中可先计算,同时在该基础上发现一般性规律,结合同底数幂运算法则即可得出结果.
6.b(a-1)
7.6
8.540
9.5
10.3
11.
12.9
13.
14.7
∵,
∴,
∴n的值为7,
故答案为:7.
利用估算无理数大小的方法求解即可。
15.
16.6
17.7
18.4
19.
20.80
21.1.5×108
解:地球与太阳的距离:.
故答案为:1.5×108.
科学记数法的表示形式为a×10n的形式,其中1≤|a|<10,n为整数.确定n的值时,要看把原数变成a时,小数点移动了多少位,n的绝对值与小数点移动的位数相同.当原数绝对值>1时,n是正数;当原数的绝对值<1时,n是负数.
22.
,
故答案为:.
利用积的乘方和幂的乘方的计算方法逐项分析判断即可.
23.2
解:由,
∴,
解得:x-y=2,
故填:2.
由题干条件联想平方差公式变形可直接联系条件与问题得出结果.
24.14
25.-12m4n3
26.
27.
28.
29.6
解: 边长为的正方形先向上平移,
平移后的阴影部分的宽为2cm,
再向右平移,得到正方形,
平移后的阴影部分的长为3cm,
此时阴影部分的面积为3×2=6cm2.
故答案为:6.
根据平移的距离求出平移后的阴影部分的长和宽,再用长×宽即可得到阴影部分的面积.
30.20a3b3
31.
解:.
故答案为:.
根据完全平方公式进行计算即可求解.
32.
33.26
解:∵,
∴.
故答案为:26.
根据完全平方公式得出,再代入求出答案即可.
34.
解:∵正方形的边长为,
∴正方形的面积为.
故答案为:.
根据正方形的面积公式进行计算即可.
35.
解:.
故答案为:.
根据积的乘方公式以及幂的乘方公式即可求解.
36.6
37.110°
38.60
根据平移的性质可得:DE=AB=12,BE=CF=6,S△ABC=S△DEF,
∴S梯形ABEO+S△OEC=S梯形DOCF+S△OEC,OE=DE-OD=12-4=8,
∴S梯形ABEO=S梯形DOCF,
∴S阴影=S梯形ABEO=(OE+AB)×BE=×(8+12)×6=60,
故答案为:60.
利用平移的性质求出S梯形ABEO=S梯形DOCF,再利用梯形的面积公式列出算式求解即可.
39.1,2,3
40.>
41.2+1
42.10
43.±4
44.20
解:∵,
∴.
故答案为:20.
根据同底数幂相乘的逆运算把3a+b转化为乘法,再整体代入计算即可.
45.15
设大正方形和小正方形的边长各为a,b,
根据题意可得:a2-b2=30,
∴阴影部分的面积=
=
=
=
=15,
故答案为:15.
设大正方形和小正方形的边长各为a,b,根据题意可得:a2-b2=30,再利用割补法求出阴影部分的面积===15即可.
46.<
∵,,32<81,
∴<,
故答案为:<.
先利用幂的乘方将和化简,再比较大小即可.
47.6
∵,,
∴,
故答案为:6.
利用同底数幂的乘法的计算方法分析求解即可.
48.;
49.
50.10
解:设大正方形的边长为,小正方形的边长为,
由题意和图可知:,,,,
∴
;
故答案为:10.
设大正方形的边长为,小正方形的边长为,先求得,,再将阴影部分的面积转化为用表示的形式,再整体代入求值.
同课章节目录
