期中真题专项复习03 证明题(含答案)--2024-2025学年八年级数学下册(湘教版)
文档属性
| 名称 | 期中真题专项复习03 证明题(含答案)--2024-2025学年八年级数学下册(湘教版) |

|
|
| 格式 | docx | ||
| 文件大小 | 418.9KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-03-30 00:00:00 | ||
图片预览

文档简介
2024-2025学年八年级数学下册(湘教版)
期中真题专项复习03 证明题
一、证明题
1.(2024八下·长沙期中)在中,.
(1)若,点M、N在、上,将沿折叠,使得点C与点A重合,求折痕的长;
(2)点D在的延长线上,且,若,求证:是直角三角形.
2.(2024八下·长岭期中)如图,已知菱形中,对角线相交于点O,过点C作,过点D作,与相交于点E.
(1)求证:四边形是矩形;
(2)若,,求四边形的周长.
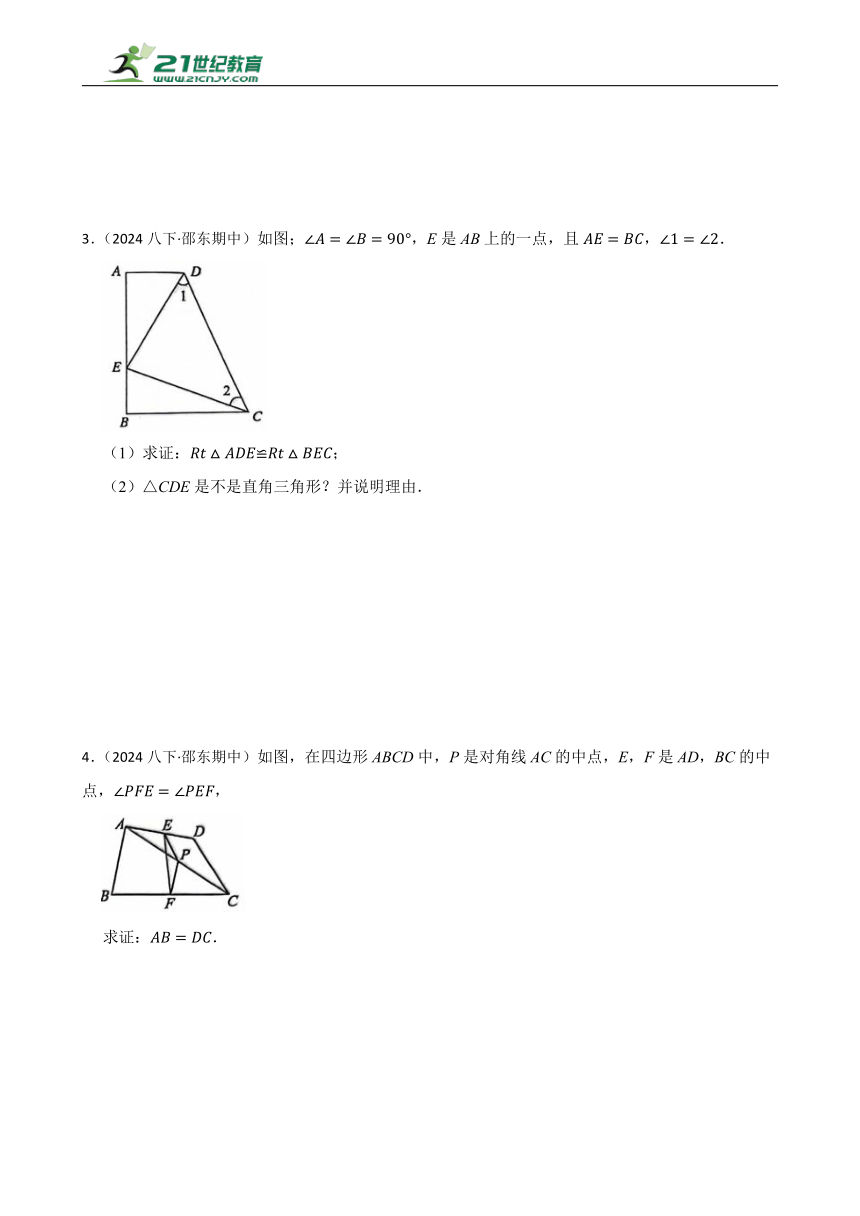
3.(2024八下·邵东期中)如图;,E是AB上的一点,且,.
(1)求证:;
(2)△CDE是不是直角三角形?并说明理由.
4.(2024八下·邵东期中)如图,在四边形ABCD中,P是对角线AC的中点,E,F是AD,BC的中点,,
求证:.
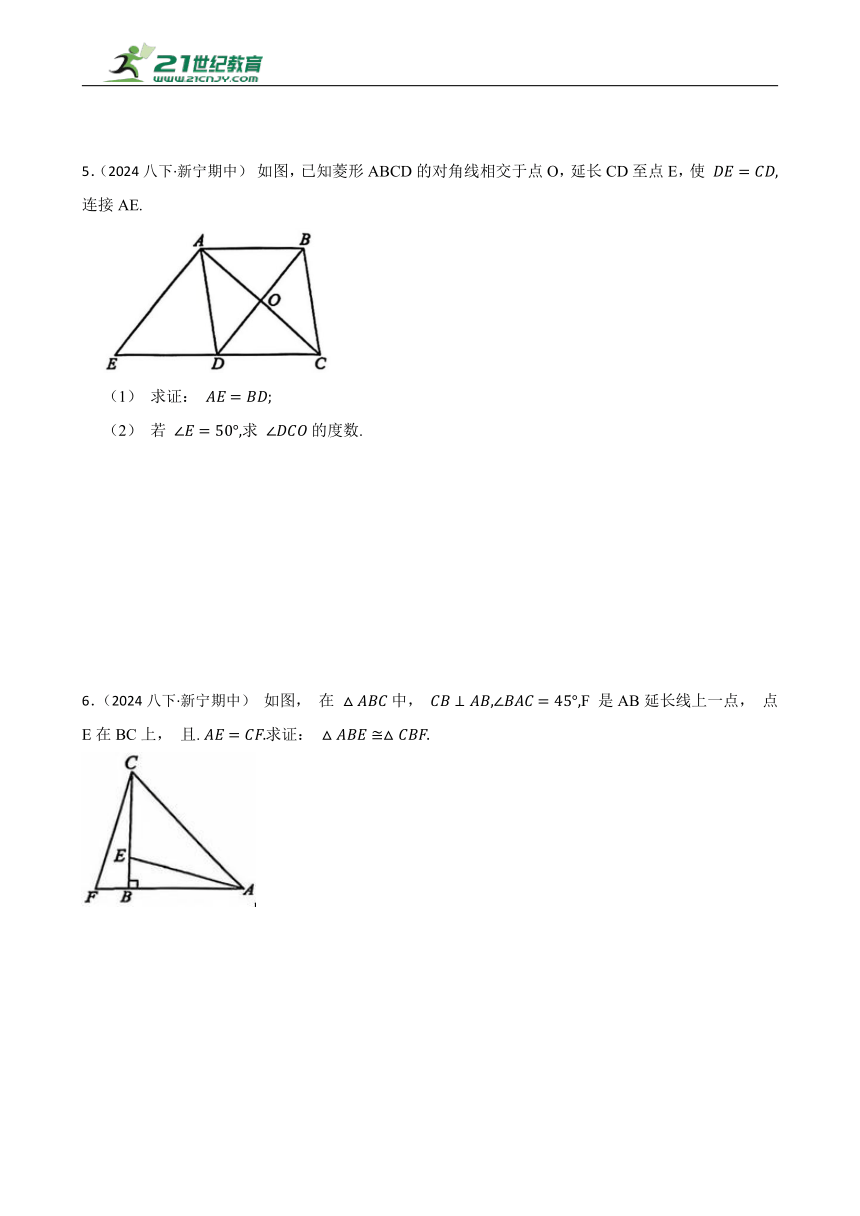
5.(2024八下·新宁期中) 如图,已知菱形ABCD的对角线相交于点O,延长CD至点E,使 连接AE.
(1) 求证:
(2) 若 求 的度数.
6.(2024八下·新宁期中) 如图, 在 中, F 是AB延长线上一点, 点E在BC上, 且. 求证:
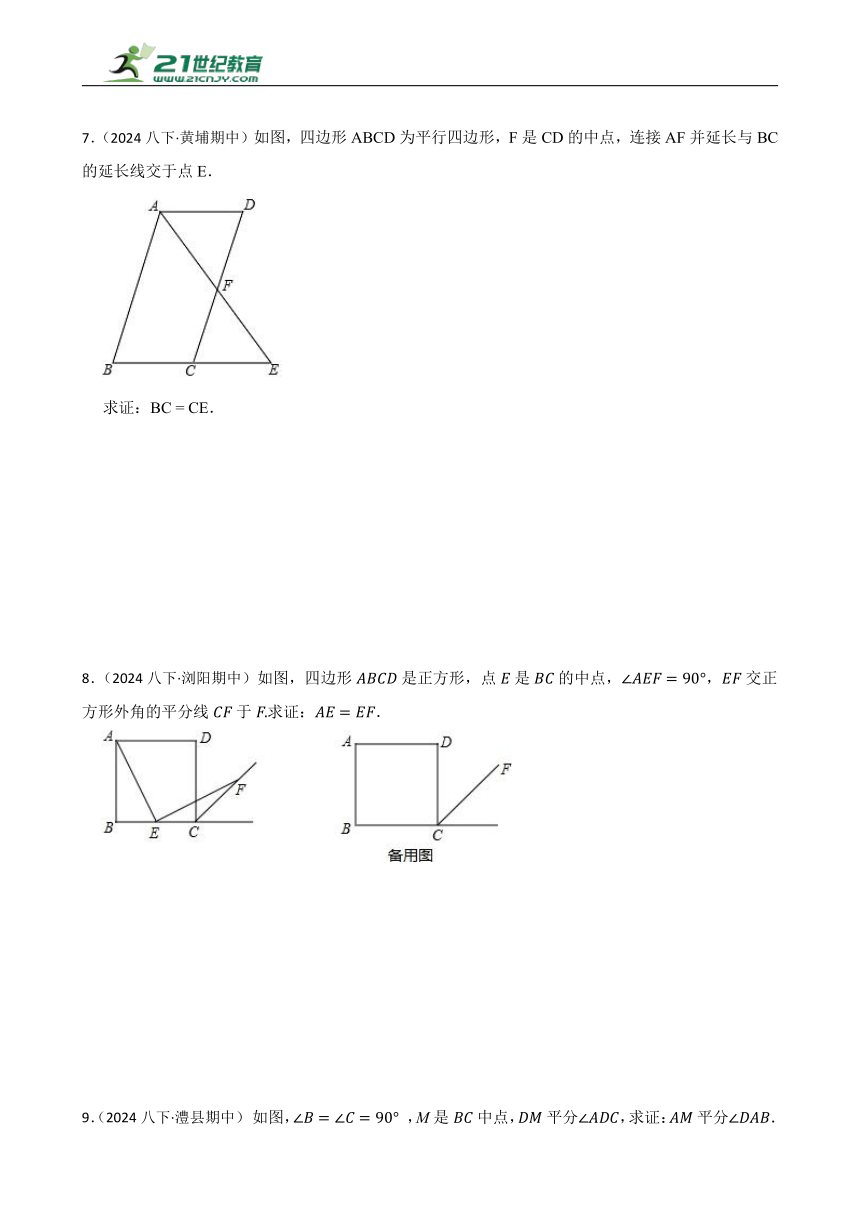
7.(2024八下·黄埔期中)如图,四边形ABCD为平行四边形,F是CD的中点,连接AF并延长与BC的延长线交于点E.
求证:BC = CE.
8.(2024八下·浏阳期中)如图,四边形是正方形,点是的中点,,交正方形外角的平分线于求证:.
9.(2024八下·澧县期中) 如图, ,M是中点,平分,求证:平分.
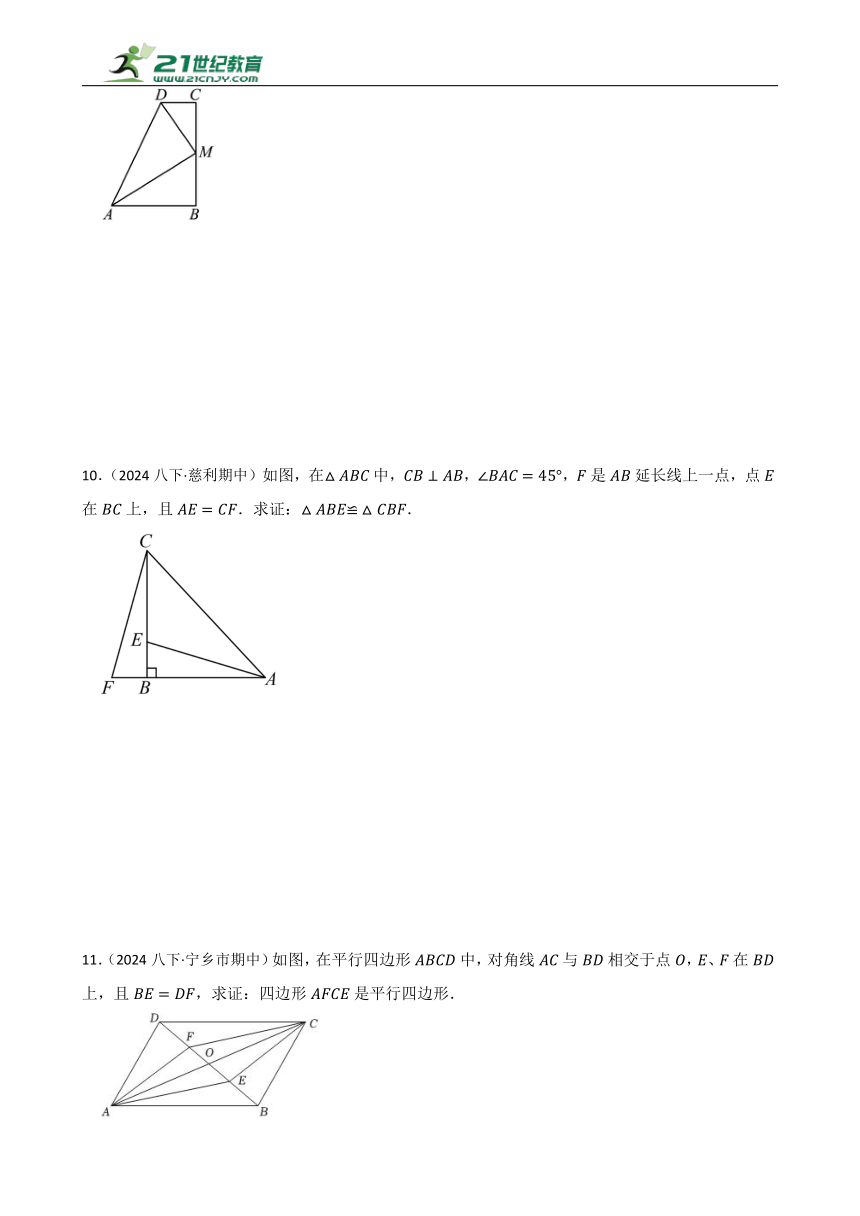
10.(2024八下·慈利期中)如图,在中,,,是延长线上一点,点在上,且.求证:.
11.(2024八下·宁乡市期中)如图,在平行四边形中,对角线与相交于点,、在上,且,求证:四边形是平行四边形.
12.(2024八下·宁乡市期中)如图,、是平行四边形对角线上两点,,求证:.
13.(2022八下·仙居期中)如图,在平行四边形ABCD中,AE=CF,求证:四边形BFDE是平行四边形.
14.(2024八下·长沙期中)在八下书本49页中,我们得到了三角形中位线定理:三角形的中位线平行于三角形的第三边,并且等于第三边的一半,完成以下证明过程:
已知:如图,D、E分别是的边,的中点;
求证:且.
证明:如图,延长到点F,使,连接,,.
∵______,,
∴四边形是平行四边形,( )(填推理的依据)
平行且等于,∴平行且等于.
∴四边形是平行四边形,( )(填推理的依据)
∴平行且等于.又∵,∴,.
15.(2024八下·新晃期中)如图,已知E,F是平行四边形ABCD对角线BD上的点,∠1=∠2.
(1)求证:;
(2)求证:四边形AECF是平行四边形.
16.(2024八下·新晃期中)如图,在和中,,联结AC与BD交于点O,M,N分别是AC、BD的中点.求证:MN垂直平分BD.
17.(2024八下·岳塘期中)已知:如图,在 中,、的平分线分别交对角线于点、求证:四边形是平行四边形.
18.(2024八下·长沙期中)如图,矩形ABCD的对角线AC、BD相交于点O,,.
(1)求证:四边形AOBE是菱形;
(2)若,,求菱形AOBE的面积.
19.(2024八下·桂阳期中)已知∠MAN=120°,AC平分∠MAN,点B、D分别在AN、AM上.
(1)如图1,若∠ABC=∠ADC=90°,请你探索线段AD、AB、AC之间的数量关系,并证明之;
(2)如图2,若∠ABC+∠ADC=180°,则(1)中的结论是否仍然成立?若成立,给出证明;若不成立,请说明理由.
20.(2024八下·宝安期中)已知:如图,,垂足分别为N,M,与相交于点P.求证:.
答案解析部分
1.(1)解:如图1,过作于,
,,
,
,
将沿折叠,使得点与点重合,
,,
设,
,
,
,
解得:,
(2)解:如图2,过作于,
,
,
,
设,,,
,
,,
,,
联立方程组解得,(负值舍去),
,
,
是直角三角形
(1)如图1,过作于,根据等腰三角形的性质得到,求得,根据折叠的性质得到,,设,根据勾股定理即可得到结论;
(2)如图2,过作于,根据等腰三角形的性质得到,设,,,得到,根据勾股定理和勾股定理的逆定理即可得到结论.
(1)如图1,过作于,
,,
,
,
将沿折叠,使得点与点重合,
,,
设,
,
,
,
解得:,
;
(2)如图2,过作于,
,
,
,
设,,,
,
,,
,,
联立方程组解得,(负值舍去),
,
,
是直角三角形.
2.(1)解:∵四边形为菱形,
∴;
∵,,
∴∠OCE=180°-∠COD=90°,∠OCE=180°-∠COD=90°,
∴四边形是矩形.
(2)解:∵四边形为菱形,
∴,,,
由勾股定理得:
,而,
∴,
∴四边形的周长.
(1)首先根据菱形的性质得到,然后利用平行线的性质可推出,根据有三个角是直角的四边形是矩形;
(2)根据菱形的性质得到,,,然后利用勾股定理得到,再利用矩形的周长公式即可求解.
3.(1)证明:,,
,
在Rt△ADE和Rt△BEC中,
,
(2)解:△CDE是直角三角形,理由如下:
证明:由(1)得,
,
,
,
,
,
△DEC为直角三角形.
(1)根据“等角对等边”,由已知条件∠1=∠2,可以得到ED=CE,根据HL证明Rt△ADE和Rt△BEC全等解答即可;
(2)根据全等三角形的性质、直角三角形的两个锐角互余及平角的定义解答即可.
4.证明:在△ABC中,P,F是AC,BC的中点,
PF是△ABC的中位线,
,同理,
,
,
根据三角形中位线定理得到,,根据∠PEF=∠PFE得到PF=PE,等量代换可得到结论.
5.(1)∵四边形ABCD是菱形,
∴AB∥CD, ∵DE=CD, ∵DE=CD, ∴AB=DE,
∴四边形ABDE是平行四边形,
∴AE=BD;
(2)由(1) 可知,∵ 四边形ABDE是平行四边形,
∴AE∥BD, ∴∠ODC=∠E=50°,
∵四边形ABCD是菱形,
∴AC⊥BD,
∴∠COD=90°,
∴∠DCO=90°-∠ODC=90°-50°=40°
(1)利用菱形的性质说明AB//CD,结合DE=CD,可说明四边形ABDE是平行四边形,从而有AE=BD成立;
(2)先根据平行四边形的性质说明AE//BD,再利用平行线的性质求出∠ODC,根据菱形的性质说明∠COD=90°,最后利用直角三角形的性质求出∠DCO.
6.解:∵ 在 中,
∴△ABC是等腰直角三角形,AB=BC,
又,
∴
先利用等腰直角三角形判断与性质说明AB=AC,且结合,可以利用HL说明
7.证明:∵四边形ABCD是平行四边形,
∴AD=BC,AD∥BC,
∴∠DAF=∠E,∠ADF=∠ECF,
又∵F是CD的中点,即DF=CF,
∴△ADF≌△ECF,
∴AD=CE,
∴BC=CE.证明:
根据平行四边形性质可得AD=BC,AD∥BC,则∠DAF=∠E,∠ADF=∠ECF,再根据全等三角形判定定理可得△ADF≌△ECF,则AD=CE,即BC=CE,即可求出答案.
8.证明:取的中点,连接;
,
,
四边形是正方形,
,
,
是的中点,是的中点,
,
,
是的角平分线,
,
,
在和中,
,
≌,
.
取的中点,连接,先求出,,再结合AH=EC,利用“ASA”证出≌, 最后利用全等三角形的性质可得.
9.证明:过点M作于点E,
∵,,平分,
∴,
∵M为中点,
∴,
又,
∴,
又∵,,
∴平分.
过点M作于点E,由角平分线的性质可得,结合线段的中点可推出,由,,根据角平分线的判定即证结论.
10.证明:,
,
,
为等腰直角三角形,
在和中,
根据三角形内角和定理可得 ,根据等腰直角三角形判定定理可得为等腰直角三角形,则,再根据全等三角形判定定理即可求出答案.
11.证明:四边形为平行四边形,
,.
,
.
四边形为平行四边形.
利用平行四边形的性质可得,,再利用对角线互相平分的四边形是平行四边形的判断方法分析求解即可.
12.证明:平行四边形中,,,
.
又,
,
≌,
.
先证出≌,再利用全等三角形的性质可得.
13.解:∵四边形ABCD为平行四边形
∴AB∥CD,AB=CD
∵AE=CF
∴DF=EB
∵DF=EB,AB∥CD,
∴四边形ABCD为平行四边形。
根据平行四边形的判定定理,一组对边平行且相等的四边形是平行四边形,即可进行证明。
14.;对角线互相平分的四边形是平行四边形;一组对边平行且相等的四边形是平行四边形.
15.(1)证明:∵四边形ABCD是平行四边形,
∴,,
∴.
∵∠1=∠2,
∴=.
在和中
,
∴,
∴;
(2)证明:∵,
∴,
∵∠1=∠2,
∴,
∴四边形AECF是平行四边形.
(1)根据平行四边形的性质准备条件,根据AAS证明三角形ABE和CFD全等,根据全等三角形的性质即可得证;
(2)根据全等三角形的性质可得AE=CF,根据平行线的判定证AE∥CF,根据一组对边平行且相等的四边形是平行四边形求证即可。
16.解:连接,如图所示
,M是的中点
又 N分别是的中点
垂直平分。
连接BM和DM,根据直角三角形斜边上的中线等于斜边的一半可得BM=DM,再根据等腰三角形的三线合一即可证明。
17.证明:四边形是平行四边形,
,,,
平分,平分,
,,
,,
在和中,
,
≌,
,,
,,
,
,
四边形是平行四边形.
利用平行四边形的性质和角平分线的定义得到角度和边长的数量关系,根据这些数量关系证明和全等;利用全等的性质得到BM=DN,;再利用角度的数量关系证明BM∥DN ,从而根据平行四边形的判定,即可证明得到四边形是平行四边形.
18.(1)证明过程见解答;(2)
19.(1)AD+AB=AC;(2)仍成立.
20.证明:如图,连接
,
.
连接OP,先利用“HL”证出,再利用全等三角形的性质可得.
期中真题专项复习03 证明题
一、证明题
1.(2024八下·长沙期中)在中,.
(1)若,点M、N在、上,将沿折叠,使得点C与点A重合,求折痕的长;
(2)点D在的延长线上,且,若,求证:是直角三角形.
2.(2024八下·长岭期中)如图,已知菱形中,对角线相交于点O,过点C作,过点D作,与相交于点E.
(1)求证:四边形是矩形;
(2)若,,求四边形的周长.
3.(2024八下·邵东期中)如图;,E是AB上的一点,且,.
(1)求证:;
(2)△CDE是不是直角三角形?并说明理由.
4.(2024八下·邵东期中)如图,在四边形ABCD中,P是对角线AC的中点,E,F是AD,BC的中点,,
求证:.
5.(2024八下·新宁期中) 如图,已知菱形ABCD的对角线相交于点O,延长CD至点E,使 连接AE.
(1) 求证:
(2) 若 求 的度数.
6.(2024八下·新宁期中) 如图, 在 中, F 是AB延长线上一点, 点E在BC上, 且. 求证:
7.(2024八下·黄埔期中)如图,四边形ABCD为平行四边形,F是CD的中点,连接AF并延长与BC的延长线交于点E.
求证:BC = CE.
8.(2024八下·浏阳期中)如图,四边形是正方形,点是的中点,,交正方形外角的平分线于求证:.
9.(2024八下·澧县期中) 如图, ,M是中点,平分,求证:平分.
10.(2024八下·慈利期中)如图,在中,,,是延长线上一点,点在上,且.求证:.
11.(2024八下·宁乡市期中)如图,在平行四边形中,对角线与相交于点,、在上,且,求证:四边形是平行四边形.
12.(2024八下·宁乡市期中)如图,、是平行四边形对角线上两点,,求证:.
13.(2022八下·仙居期中)如图,在平行四边形ABCD中,AE=CF,求证:四边形BFDE是平行四边形.
14.(2024八下·长沙期中)在八下书本49页中,我们得到了三角形中位线定理:三角形的中位线平行于三角形的第三边,并且等于第三边的一半,完成以下证明过程:
已知:如图,D、E分别是的边,的中点;
求证:且.
证明:如图,延长到点F,使,连接,,.
∵______,,
∴四边形是平行四边形,( )(填推理的依据)
平行且等于,∴平行且等于.
∴四边形是平行四边形,( )(填推理的依据)
∴平行且等于.又∵,∴,.
15.(2024八下·新晃期中)如图,已知E,F是平行四边形ABCD对角线BD上的点,∠1=∠2.
(1)求证:;
(2)求证:四边形AECF是平行四边形.
16.(2024八下·新晃期中)如图,在和中,,联结AC与BD交于点O,M,N分别是AC、BD的中点.求证:MN垂直平分BD.
17.(2024八下·岳塘期中)已知:如图,在 中,、的平分线分别交对角线于点、求证:四边形是平行四边形.
18.(2024八下·长沙期中)如图,矩形ABCD的对角线AC、BD相交于点O,,.
(1)求证:四边形AOBE是菱形;
(2)若,,求菱形AOBE的面积.
19.(2024八下·桂阳期中)已知∠MAN=120°,AC平分∠MAN,点B、D分别在AN、AM上.
(1)如图1,若∠ABC=∠ADC=90°,请你探索线段AD、AB、AC之间的数量关系,并证明之;
(2)如图2,若∠ABC+∠ADC=180°,则(1)中的结论是否仍然成立?若成立,给出证明;若不成立,请说明理由.
20.(2024八下·宝安期中)已知:如图,,垂足分别为N,M,与相交于点P.求证:.
答案解析部分
1.(1)解:如图1,过作于,
,,
,
,
将沿折叠,使得点与点重合,
,,
设,
,
,
,
解得:,
(2)解:如图2,过作于,
,
,
,
设,,,
,
,,
,,
联立方程组解得,(负值舍去),
,
,
是直角三角形
(1)如图1,过作于,根据等腰三角形的性质得到,求得,根据折叠的性质得到,,设,根据勾股定理即可得到结论;
(2)如图2,过作于,根据等腰三角形的性质得到,设,,,得到,根据勾股定理和勾股定理的逆定理即可得到结论.
(1)如图1,过作于,
,,
,
,
将沿折叠,使得点与点重合,
,,
设,
,
,
,
解得:,
;
(2)如图2,过作于,
,
,
,
设,,,
,
,,
,,
联立方程组解得,(负值舍去),
,
,
是直角三角形.
2.(1)解:∵四边形为菱形,
∴;
∵,,
∴∠OCE=180°-∠COD=90°,∠OCE=180°-∠COD=90°,
∴四边形是矩形.
(2)解:∵四边形为菱形,
∴,,,
由勾股定理得:
,而,
∴,
∴四边形的周长.
(1)首先根据菱形的性质得到,然后利用平行线的性质可推出,根据有三个角是直角的四边形是矩形;
(2)根据菱形的性质得到,,,然后利用勾股定理得到,再利用矩形的周长公式即可求解.
3.(1)证明:,,
,
在Rt△ADE和Rt△BEC中,
,
(2)解:△CDE是直角三角形,理由如下:
证明:由(1)得,
,
,
,
,
,
△DEC为直角三角形.
(1)根据“等角对等边”,由已知条件∠1=∠2,可以得到ED=CE,根据HL证明Rt△ADE和Rt△BEC全等解答即可;
(2)根据全等三角形的性质、直角三角形的两个锐角互余及平角的定义解答即可.
4.证明:在△ABC中,P,F是AC,BC的中点,
PF是△ABC的中位线,
,同理,
,
,
根据三角形中位线定理得到,,根据∠PEF=∠PFE得到PF=PE,等量代换可得到结论.
5.(1)∵四边形ABCD是菱形,
∴AB∥CD, ∵DE=CD, ∵DE=CD, ∴AB=DE,
∴四边形ABDE是平行四边形,
∴AE=BD;
(2)由(1) 可知,∵ 四边形ABDE是平行四边形,
∴AE∥BD, ∴∠ODC=∠E=50°,
∵四边形ABCD是菱形,
∴AC⊥BD,
∴∠COD=90°,
∴∠DCO=90°-∠ODC=90°-50°=40°
(1)利用菱形的性质说明AB//CD,结合DE=CD,可说明四边形ABDE是平行四边形,从而有AE=BD成立;
(2)先根据平行四边形的性质说明AE//BD,再利用平行线的性质求出∠ODC,根据菱形的性质说明∠COD=90°,最后利用直角三角形的性质求出∠DCO.
6.解:∵ 在 中,
∴△ABC是等腰直角三角形,AB=BC,
又,
∴
先利用等腰直角三角形判断与性质说明AB=AC,且结合,可以利用HL说明
7.证明:∵四边形ABCD是平行四边形,
∴AD=BC,AD∥BC,
∴∠DAF=∠E,∠ADF=∠ECF,
又∵F是CD的中点,即DF=CF,
∴△ADF≌△ECF,
∴AD=CE,
∴BC=CE.证明:
根据平行四边形性质可得AD=BC,AD∥BC,则∠DAF=∠E,∠ADF=∠ECF,再根据全等三角形判定定理可得△ADF≌△ECF,则AD=CE,即BC=CE,即可求出答案.
8.证明:取的中点,连接;
,
,
四边形是正方形,
,
,
是的中点,是的中点,
,
,
是的角平分线,
,
,
在和中,
,
≌,
.
取的中点,连接,先求出,,再结合AH=EC,利用“ASA”证出≌, 最后利用全等三角形的性质可得.
9.证明:过点M作于点E,
∵,,平分,
∴,
∵M为中点,
∴,
又,
∴,
又∵,,
∴平分.
过点M作于点E,由角平分线的性质可得,结合线段的中点可推出,由,,根据角平分线的判定即证结论.
10.证明:,
,
,
为等腰直角三角形,
在和中,
根据三角形内角和定理可得 ,根据等腰直角三角形判定定理可得为等腰直角三角形,则,再根据全等三角形判定定理即可求出答案.
11.证明:四边形为平行四边形,
,.
,
.
四边形为平行四边形.
利用平行四边形的性质可得,,再利用对角线互相平分的四边形是平行四边形的判断方法分析求解即可.
12.证明:平行四边形中,,,
.
又,
,
≌,
.
先证出≌,再利用全等三角形的性质可得.
13.解:∵四边形ABCD为平行四边形
∴AB∥CD,AB=CD
∵AE=CF
∴DF=EB
∵DF=EB,AB∥CD,
∴四边形ABCD为平行四边形。
根据平行四边形的判定定理,一组对边平行且相等的四边形是平行四边形,即可进行证明。
14.;对角线互相平分的四边形是平行四边形;一组对边平行且相等的四边形是平行四边形.
15.(1)证明:∵四边形ABCD是平行四边形,
∴,,
∴.
∵∠1=∠2,
∴=.
在和中
,
∴,
∴;
(2)证明:∵,
∴,
∵∠1=∠2,
∴,
∴四边形AECF是平行四边形.
(1)根据平行四边形的性质准备条件,根据AAS证明三角形ABE和CFD全等,根据全等三角形的性质即可得证;
(2)根据全等三角形的性质可得AE=CF,根据平行线的判定证AE∥CF,根据一组对边平行且相等的四边形是平行四边形求证即可。
16.解:连接,如图所示
,M是的中点
又 N分别是的中点
垂直平分。
连接BM和DM,根据直角三角形斜边上的中线等于斜边的一半可得BM=DM,再根据等腰三角形的三线合一即可证明。
17.证明:四边形是平行四边形,
,,,
平分,平分,
,,
,,
在和中,
,
≌,
,,
,,
,
,
四边形是平行四边形.
利用平行四边形的性质和角平分线的定义得到角度和边长的数量关系,根据这些数量关系证明和全等;利用全等的性质得到BM=DN,;再利用角度的数量关系证明BM∥DN ,从而根据平行四边形的判定,即可证明得到四边形是平行四边形.
18.(1)证明过程见解答;(2)
19.(1)AD+AB=AC;(2)仍成立.
20.证明:如图,连接
,
.
连接OP,先利用“HL”证出,再利用全等三角形的性质可得.
同课章节目录
