期中真题专项复习01选择题(含答案)--2024-2025学年八年级数学下册(湘教版)
文档属性
| 名称 | 期中真题专项复习01选择题(含答案)--2024-2025学年八年级数学下册(湘教版) |

|
|
| 格式 | docx | ||
| 文件大小 | 774.3KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-03-30 00:00:00 | ||
图片预览


文档简介
2024-2025学年八年级数学下册(湘教版)
期中真题专项复习01选择题
一、选择题
1.(2020八下·长沙期中)如图,在菱形ABCD中,P、Q分别是AD、AC的中点,如果 ,那么菱形ABCD的周长是( )
A.16 B.8 C.4 D.2
2.(2024八下·湘西期中)已知一个菱形的两条对角线长分别是12,,则这个菱形的面积为( )
A. B. C. D.36
3.(2022八下·新建期中)如图,在中,,D,E分别为,的中点,平分,交于点F,若,则的长为( )
A. B.1 C. D.2
4.(2023八下·岳阳期中)在平面直角坐标系中,对于点,我们把点叫做点伴随点.已知点的伴随点为,点的伴随点为,点的伴随点为,…,这样依次得到点,,,…,,….若点的坐标为,点的坐标为( )
A. B. C. D.
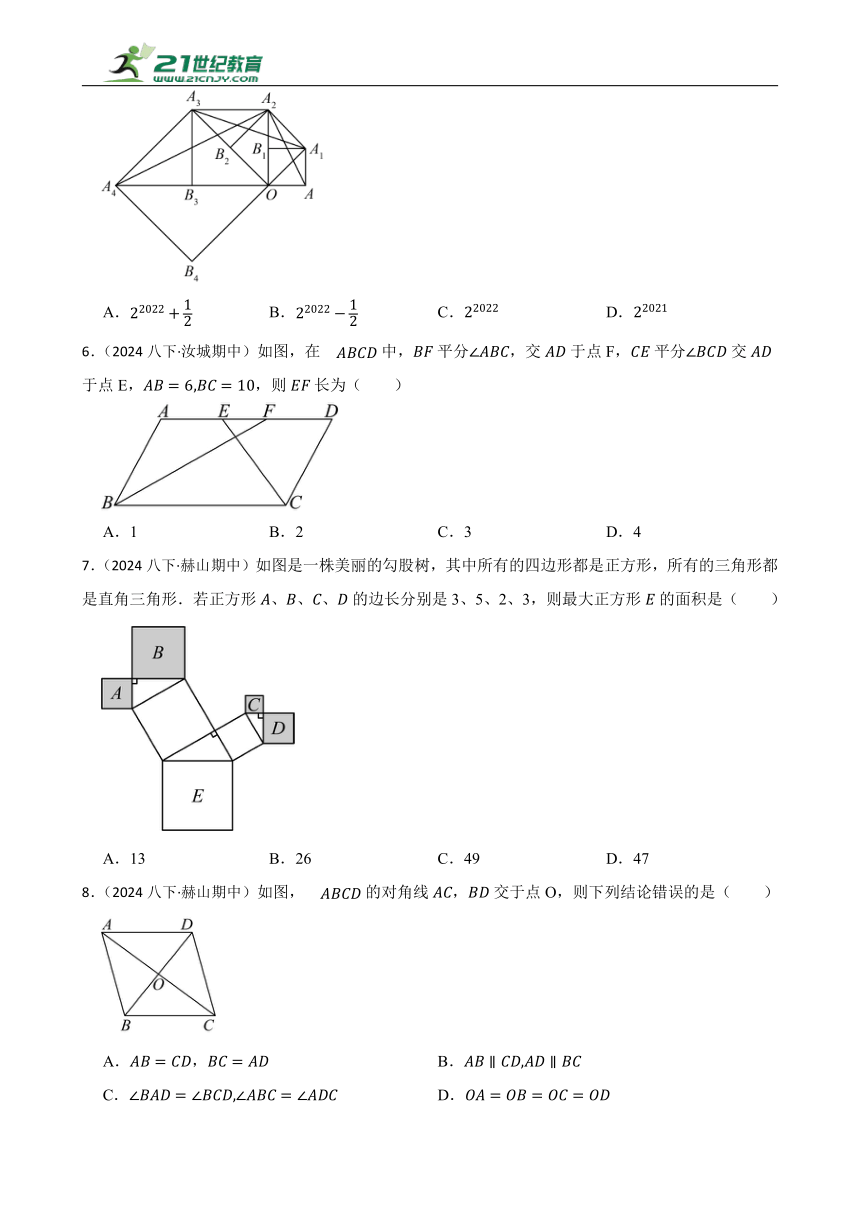
5.(2024八下·湘西期中)如图,四边形是边长为1的正方形,以对角线为边作第二个正方形,连接,得到;再以对角线为边作第三个正方形,连接,得到;再以对角线为边作第四个正方形,连接,得到;….设的面积分别为依此下去,则的值为( )
A. B. C. D.
6.(2024八下·汝城期中)如图,在中,平分,交于点F,平分交于点E,,则长为( )
A.1 B.2 C.3 D.4
7.(2024八下·赫山期中)如图是一株美丽的勾股树,其中所有的四边形都是正方形,所有的三角形都是直角三角形.若正方形、、、的边长分别是3、5、2、3,则最大正方形的面积是( )
A.13 B.26 C.49 D.47
8.(2024八下·赫山期中)如图,的对角线,交于点O,则下列结论错误的是( )
A., B.
C. D.
9.(2024八下·赫山期中)如图,四边形是平行四边形,下列结论中错误的是( )
A.当,平行四边形是矩形
B.当,平行四边形是矩形
C.当,平行四边形是菱形
D.当,平行四边形是正方形
10.(2024八下·赫山期中)下列图形中,既是轴对称图形又是中心对称图形的是( )
A. B.
C. D.
11.(2024八下·天元期中)如图,是正方形的边延长线上的一点,且交于点,则的度数为( )
A. B. C. D.
12.(2024八下·湖南期中)下列几组数中,能作为直角三角形三边长度的是( )
A.2、3、4 B.3、4、5 C.4、5、6 D.7、8、9
13.(2024八下·汕头期中)如图,在中,,点D,E分别为,的中点,则( )
A. B. C.1 D.2
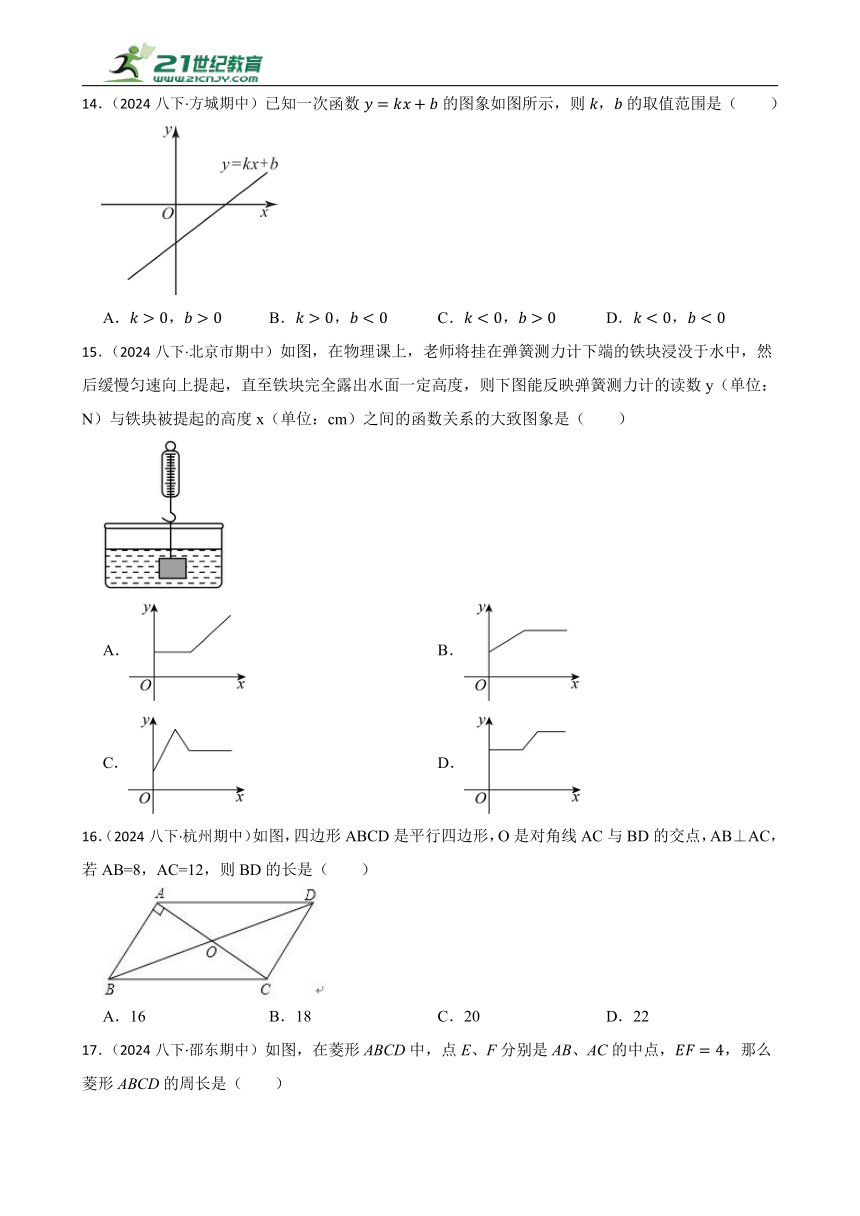
14.(2024八下·方城期中)已知一次函数的图象如图所示,则,的取值范围是( )
A., B., C., D.,
15.(2024八下·北京市期中)如图,在物理课上,老师将挂在弹簧测力计下端的铁块浸没于水中,然后缓慢匀速向上提起,直至铁块完全露出水面一定高度,则下图能反映弹簧测力计的读数y(单位:N)与铁块被提起的高度x(单位:cm)之间的函数关系的大致图象是( )
A. B.
C. D.
16.(2024八下·杭州期中)如图,四边形ABCD是平行四边形,O是对角线AC与BD的交点,AB⊥AC,若AB=8,AC=12,则BD的长是( )
A.16 B.18 C.20 D.22
17.(2024八下·邵东期中)如图,在菱形ABCD中,点E、F分别是AB、AC的中点,,那么菱形ABCD的周长是( )
A.16 B.24 C.28 D.32
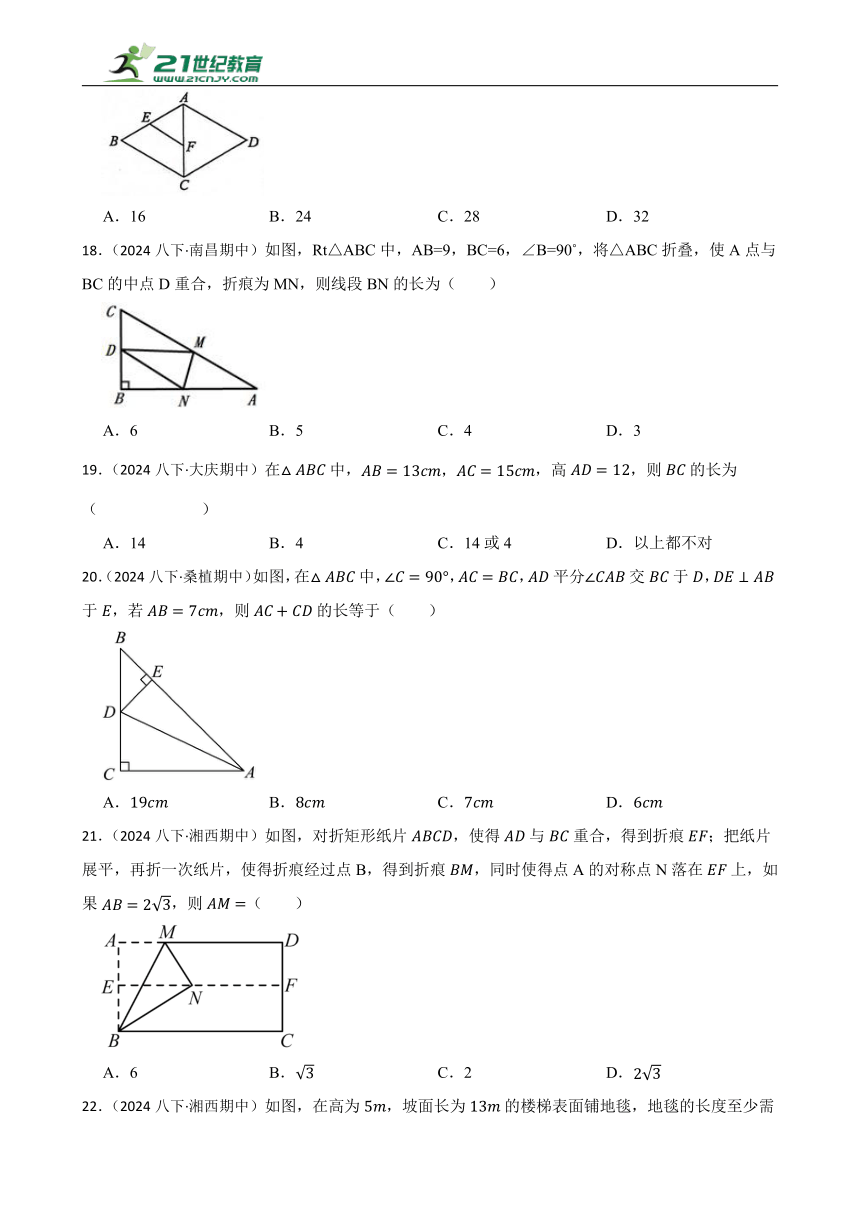
18.(2024八下·南昌期中)如图,Rt△ABC中,AB=9,BC=6,∠B=90 ,将△ABC折叠,使A点与BC的中点D重合,折痕为MN,则线段BN的长为( )
A.6 B.5 C.4 D.3
19.(2024八下·大庆期中)在中,,高,则的长为( )
A.14 B.4 C.14或4 D.以上都不对
20.(2024八下·桑植期中)如图,在中,,,平分交于,于,若,则的长等于( )
A. B. C. D.
21.(2024八下·湘西期中)如图,对折矩形纸片,使得与重合,得到折痕;把纸片展平,再折一次纸片,使得折痕经过点B,得到折痕,同时使得点A的对称点N落在上,如果,则( )
A.6 B. C.2 D.
22.(2024八下·湘西期中)如图,在高为,坡面长为的楼梯表面铺地毯,地毯的长度至少需要( )
A. B. C. D.
23.(2024八下·湘西期中)下列命题的逆命题是真命题的是( )
A.若,则
B.如果两个实数相等,那么它们的绝对值相等
C.如果直角三角形的两条直角边长分别为a,b,斜边长为c,那么
D.邻补角互补.
24.(2024八下·湘西期中)在下列给出的条件中,可以判定四边形为平行四边形的条件是( )
A., B.,
C., D.,
25.(2024八下·冷水滩期中)已知直角三角形的两直角边长为3和4,则这个直角三角形的斜边长为( )
A.5 B.7 C.10 D.12
26.(2024八下·冷水滩期中)如图所示,在中,,,则的度数为( )
A. B. C. D.
27.(2024八下·冷水滩期中)中国瓷器,积淀了深厚的文化底蕴,是中国传统艺术文化的重要组成部分.瓷器上的图案设计精美,极富变化.下面瓷器图案中,既是轴对称图形又是中心对称图形的是( )
A. B.
C. D.
28.(2024八下·湖南期中)如图,在边长为的正方形中,是边的中点,是边上的一个动点(不与重合),以线段为边在正方形内作等边,是边的中点,连接,则在点运动过程中,的最小值是( )
A. B. C. D.
29.(2024八下·湖南期中)如图,将矩形纸片折叠,使边落在对角线上,折痕为,且D点落在对角线处,,,则的长为( )
A. B. C. D.
30.(2024八下·湖南期中)如图,在中,,以的三边为边向外作正方形,其面积分别为,,,,,则( )
A.9 B.12 C.15 D.144
31.(2024八下·湖南期中)在平行四边形中,用直尺和圆规作的平分线交于点,若,,则的长为( )
A. B. C. D.
32.(2024八下·湖南期中)如图,在中,,的平分线BD交AC于点D,若,则点D到AB的距离DE是( )
A.2cm B.3cm C.4cm D.5cm
33.(2024八下·湖南期中)如图,是的中位线,若,则的度数为( )
A. B. C. D.
34.(2024八下·湖南期中)如图,已知,垂足为,,,则可得到,理由是( )
A. B. C. D.
35.(2024八下·汕头期中)两条对角线相等且互相垂直平分的四边形是( )
A.平行四边形 B.矩形
C.菱形 D.正方形
36.(2024八下·祁东期中)如图, ABCD的对角线AC与BD相交于点O,∠ADB=90°,AC=10,BD=6,则AD的长是( )
A.4 B. C.8 D.2
37.(2024八下·祁东期中)已知点在第四象限内,则一次函数的图象大致是( )
A. B.
C. D.
38.(2024八下·邵东期中)小明早晨骑自行车到学校上学,匀速骑行一段时间后,发现作业本忘在家里,于是他按原路匀速返回,半路拿到爸爸送来的作业本后,为了不耽误上学的时间,决定以更快的速度匀速骑车赶往学校,则下列最能反映小明与家的距离 s ( km )与骑行时间 t ( h )之间的函数关系的大致图象是( )
A. B.
C. D.
39.(2024八下·邵东期中)如图,,,,分别是四边形四条边的中点,要使四边形为菱形,则四边形应具备的条件是( )
A.一组对边平行而另一组对边不平行
B.对角线相等
C.对角线互相平分
D.对角线互相垂直
40.(2024八下·邵东期中)下列说法正确的是 ( )
A.一组对边平行,另一组对边相等的四边形是平行四边形.
B.对角线相等的四边形是矩形.
C.矩形是轴对称图形,两条对角线所在的直线是它的对称轴.
D.对角线互相垂直平分的四边形是菱形.
41.(2024八下·邵东期中)2023年6月4日6时33分,神舟十五号载人飞船返回舱在东风着陆场平安着陆,神舟十五号载人飞行任务取得圆满成功,展现了中国航天科技的新高度.下列航天图标,其文字上方的图案是中心对称图形的是( )
A. B.
C. D.
42.(2024八下·浏阳期中)如图,在△ABC中,点D,E,F分别在边BC,AB,AC上,且DE∥CA,DF∥BA,下列说法不正确是( )
A.若AD=EF,那么四边形AEDF是矩形
B.若AD平分∠BAC,那么四边形AEDF是菱形
C.若AD⊥BC且AB=AC,那么四边形AEDF是菱形
D.若∠ADC=90°,那么四边形AEDF是矩形
43.(2024八下·浏阳期中)如图,在四边形ABCD中,∠ABC为直角,AB∥CD,AB=CD,对角线AC、BD相交于点O,AB=5,AO=6.5,则四边形ABCD的面积为( )
A.60 B.30 C.90 D.96
44.(2024八下·浏阳期中)如图,已知线段AB、AD和射线BP,且AD∥BP,在射线BP上找一点C,使得四边形ABCD是平行四边形,下列作法不一定可行的是( )
A.过点D作DC∥AB与BP交于点C
B.在AD下方作∠ADC与BP交于点C,使∠ADC=∠ABP
C.在BP上截取BC,使BC=AD,连接DC
D.以点D为圆心,AB长为半径画弧,与BP交于点C,连接DC
45.(2024八下·永兴期中)下列几组数中,能作为直角三角形三边长度的是( )
A.4,5,6 B.1,,3 C.6,8,10 D.5,12,22
46.(2024八下·永兴期中)下列图形中,是轴对称图形又是中心对称图形的是( )
A. B. C. D.
47.(2024八下·澧县期中) 如图,当秋千静止时,踏板离地的垂直高度,将它往前推至处时(即水平距离,),踏板离地的垂直高度,它的绳索始终拉直,则绳索的长是( )
A. B. C. D.
48.(2024八下·澧县期中) 如图,△ABC中,∠ACB=90°,CD是高,∠A=30°,则BD与AB的关系( )
A.BD=AB B.BD=AB C.BD=AB D.BD=AB
49.(2024八下·慈利期中)如图,在中,,,,为边上一动点,于,于,为的中点,则的最小值为
A. B. C. D.
50.(2024八下·长沙期中)如图,在正方形ABCD外取一点,连接AE,BE,DE.过点作AE的垂线交DE于点.若,.下列结论:
①;②点到直线AE的距离是;③;④.其中正确的结论个数是( )
A.4 B.3 C.2 D.1
答案解析部分
1.A
解:∵P、Q分别是AD、AC的中点,
∴CD=2PQ=4,
∴菱形ABCD的周长是4×4=16.
故答案为:A.
根据三角形的中位线定理,即可求得CD的长,进而求得菱形的周长.
2.B
3.B
4.B
解:∵点的坐标为,点的伴随点为,
∴,
∴,
∴,
∴,
∴的坐标周期变化,周期为4,
∵,
∴,
故答案为:B.
先分别计算出,,,,的坐标,得出坐标的周期为4,即可求解.
5.C
6.B
解:如图:
∵,
∴,
∴,
∵平分,平分,
∴,
∴,
∴,
∴,
∴;
故答案为:B.
证明,利用等角对等边得:,进而得到,再利用平行四边形的性质得AD长,即可得解.
7.D
8.D
9.D
10.C
11.D
12.B
13.D
14.B
15.D
16.C
解:∵四边形ABCD是平行四边形,AC=12,
∴OA=AC=6,BD=2OB,
∵AB⊥AC,AB=8,
∴OB==10,
∴BD=2OB=20.
故选C.
由四边形ABCD是平行四边形,根据平行四边形的对角线互相平分,可得OA的长,然后由AB⊥AC,AB=8,AC=12,根据勾股定理可求得OB的长,继而求得答案.
17.D
解:∵点E、F分别是AB、AC的中点,EF=4,
∴BC=2EF=8,
∵四边形ABCD是菱形,
∴AB=BC=CD=AD
∴菱形ABCD的周长是8×4=32.
故答案为:D.
由E、F分别是AB、AC的中点可知EF为△ABC的中位线,利用三角形的中位线的定理:三角形的中位线平行于三角形的第三边,且等于第三边的一半,即可求得BC的长,然后由菱形的性质:菱形的四条边都相等,即可求得菱形ABCD的周长.
18.C
解:设BN=x,由折叠的性质可得DN=AN=9-x,
∵D是BC的中点,
∴BD=3,
在Rt△NBD中,x2+32=(9-x)2,
解得x=4.
即BN=4.
故答案为:C.
设BN=x,则由折叠的性质可得DN=AN=9-x,根据中点的定义可得BD=3,在Rt△BND中,根据勾股定理可得关于x的方程,解方程即可求解.
19.C
20.C
21.C
22.A
23.C
24.B
25.A
26.A
27.B
28.A
29.D
30.D
31.C
32.C
33.B
34.A
35.D
解:根据正方形的判别方法知,两条对角线互相垂直平分的四边形是菱形,且相等又可判定为正方形,故选D.
两条对角线互相垂直平分的四边形是菱形,对角线相等的菱形是正方形,所以该四边形是正方形.
36.A
37.A
38.C
39.B
40.D
41.D
42.D
∵DE∥CA,DF∥BA,
∴ 四边形AEDF是平行四边形.
∵AD=EF,
∴ 四边形AEDF是矩形,故A正确;
∵四边形AEDF是平行四边形,AD平分∠BAC,
∴四边形AEDF是菱形,故B正确;
∵AD⊥BC且AB=AC,
∴AD平分∠BAC,
∵四边形AEDF是平行四边形,
∴四边形AEDF是菱形,故C正确;
四边形AEDF是平行四边形,∠ADC=90°,不能推出四边形AEDF是矩形,故D错误.
故答案为:D.
A利用对角线相等的平行四边形是矩形求解;B、C根据对角线平分一组对角的平行四边形是菱形求解;D添加条件∠ADC=90°,不能推出四边形AEDF是矩形.
43.A
解:∵AB=CD,AB//CD,
∴四边形ABCD是平行四边形.
∵∠ABC为直角,
∴四边形ABCD是矩形.
∵AB=5,AO=6.5,
∴AC=2AO=13,
∴BC=
∴四边形ABCD的面积为BA×BC=5×12=60.
故答案为:A.
先证明四边形ABCD是矩形,再求出BC,最后利用矩形面积公式求解.
44.D
解: ∵过点D作DC∥AB与BP交于点C ,AD∥BP,∴四边形ABCD是平行四边形(两组对边分别平行的四边形是平行四边形),故A不符合;
∵AD∥BP,∴∠A+∠B=180°,
∵在AD下方作∠ADC与BP交于点C,使∠ADC=∠B,
∴∠A+∠ADC=180°,∴AB//DC.
∵AD//BC,
∴四边形ABCD是平行四边形(两组对边分别平行的四边形是平行四边形),故B不符合;
∵AD∥BP, 在BP上截取BC,使BC=AD,连接DC ,
∴四边形ABCD是平行四边形(一组对边平行且相等的四边形是平行四边形),故C不符合;
以点D为圆心,AB长为半径画弧,与BP交于点C,连接DC , 且AD∥BP, 只满足一对边平行,另一对边相等,有可能是梯形,不一定是平行四边形,故D符合.
故答案为:D.
(1)根据两组对边分别平行的四边形是平行四边形;
(2)根据两组对边分别平行的四边形是平行四边形;
(3)根据一组对边平行且相等的四边形是平行四边形;
(4)满足一对边平行,另一对边相等不判断为平行四边形.
45.C
46.D
47.B
解:设AC=x,则AB=AC=x,AD=AB+BE-DE=x-2,
在Rt△ACD中,AC2=AD2+CD2,
∴x2=(x-2)2+42,
解得x=5,
故答案为:B.
设AC=x,则AB=AC=x,AD=x-2,在Rt△ACD中,根据勾股定理建立关于x方程并解之即可.
48.C
解:在 △ABC中,∠ACB=90°,∠A=30° , CD是高
∴AB=2BC,∠B=60°,∠BDC=90°,
∴∠BCD=90°-∠B=30°,
∴BC=2BD,
∴AB=4BD,即 BD=AB .
故答案为:C.
利用含30°角的直角三角形的性质可得AB=2BC,BC=2BD,从而得出AB=4BD,据此判断即可.
49.C
50.A
①∵∠EAB+∠BAP=90°,∠PAD+∠BAP=90°,
∴∠EAB=∠PAD,
在△APD和△AEB中,
,
∴△APD≌△AEB(SAS),
∴①正确,符合题意;
②过点B作BF⊥AE,交AE的延长线于点F,如图所示:
∵△APD≌△AEB,
∴∠APD=∠AEB,
∵∠APD+∠AEP=90°,
∴∠AEB+∠AEP=90°,
∴∠BEP=90°,
∴∠BEA+∠AEP=90°,
∵AE=AP=,
∴△AEP是等腰直角三角形,
∴∠AEP=45°,
∴∠BEA=45°,
∴△ABF是等腰直角三角形,
∵AE=,
∴由勾股定理可得:EP=2,
∵PB=3,
∴BE=1,
∴由勾股定理可得:BP=,
∴BF=BE=,
∴②正确,符合题意;
③∵∠BED=∠BEA+∠AEP=90°,
∴EB⊥ED,
∴③正确,符合题意;
④∵△APD≌△AEB,
∴PD=BE=1,
∴DE=3,
∴S正方形ABCD=AD2=AE2+DE2=,
∴④不正确,不符合题意;
综上,正确的结论是①②③,共3个,
故答案为:B.
利用正方形的性质,全等三角形的判定方法和性质,点到直线的距离公式及正方形的面积公式逐项分析判断即可.
期中真题专项复习01选择题
一、选择题
1.(2020八下·长沙期中)如图,在菱形ABCD中,P、Q分别是AD、AC的中点,如果 ,那么菱形ABCD的周长是( )
A.16 B.8 C.4 D.2
2.(2024八下·湘西期中)已知一个菱形的两条对角线长分别是12,,则这个菱形的面积为( )
A. B. C. D.36
3.(2022八下·新建期中)如图,在中,,D,E分别为,的中点,平分,交于点F,若,则的长为( )
A. B.1 C. D.2
4.(2023八下·岳阳期中)在平面直角坐标系中,对于点,我们把点叫做点伴随点.已知点的伴随点为,点的伴随点为,点的伴随点为,…,这样依次得到点,,,…,,….若点的坐标为,点的坐标为( )
A. B. C. D.
5.(2024八下·湘西期中)如图,四边形是边长为1的正方形,以对角线为边作第二个正方形,连接,得到;再以对角线为边作第三个正方形,连接,得到;再以对角线为边作第四个正方形,连接,得到;….设的面积分别为依此下去,则的值为( )
A. B. C. D.
6.(2024八下·汝城期中)如图,在中,平分,交于点F,平分交于点E,,则长为( )
A.1 B.2 C.3 D.4
7.(2024八下·赫山期中)如图是一株美丽的勾股树,其中所有的四边形都是正方形,所有的三角形都是直角三角形.若正方形、、、的边长分别是3、5、2、3,则最大正方形的面积是( )
A.13 B.26 C.49 D.47
8.(2024八下·赫山期中)如图,的对角线,交于点O,则下列结论错误的是( )
A., B.
C. D.
9.(2024八下·赫山期中)如图,四边形是平行四边形,下列结论中错误的是( )
A.当,平行四边形是矩形
B.当,平行四边形是矩形
C.当,平行四边形是菱形
D.当,平行四边形是正方形
10.(2024八下·赫山期中)下列图形中,既是轴对称图形又是中心对称图形的是( )
A. B.
C. D.
11.(2024八下·天元期中)如图,是正方形的边延长线上的一点,且交于点,则的度数为( )
A. B. C. D.
12.(2024八下·湖南期中)下列几组数中,能作为直角三角形三边长度的是( )
A.2、3、4 B.3、4、5 C.4、5、6 D.7、8、9
13.(2024八下·汕头期中)如图,在中,,点D,E分别为,的中点,则( )
A. B. C.1 D.2
14.(2024八下·方城期中)已知一次函数的图象如图所示,则,的取值范围是( )
A., B., C., D.,
15.(2024八下·北京市期中)如图,在物理课上,老师将挂在弹簧测力计下端的铁块浸没于水中,然后缓慢匀速向上提起,直至铁块完全露出水面一定高度,则下图能反映弹簧测力计的读数y(单位:N)与铁块被提起的高度x(单位:cm)之间的函数关系的大致图象是( )
A. B.
C. D.
16.(2024八下·杭州期中)如图,四边形ABCD是平行四边形,O是对角线AC与BD的交点,AB⊥AC,若AB=8,AC=12,则BD的长是( )
A.16 B.18 C.20 D.22
17.(2024八下·邵东期中)如图,在菱形ABCD中,点E、F分别是AB、AC的中点,,那么菱形ABCD的周长是( )
A.16 B.24 C.28 D.32
18.(2024八下·南昌期中)如图,Rt△ABC中,AB=9,BC=6,∠B=90 ,将△ABC折叠,使A点与BC的中点D重合,折痕为MN,则线段BN的长为( )
A.6 B.5 C.4 D.3
19.(2024八下·大庆期中)在中,,高,则的长为( )
A.14 B.4 C.14或4 D.以上都不对
20.(2024八下·桑植期中)如图,在中,,,平分交于,于,若,则的长等于( )
A. B. C. D.
21.(2024八下·湘西期中)如图,对折矩形纸片,使得与重合,得到折痕;把纸片展平,再折一次纸片,使得折痕经过点B,得到折痕,同时使得点A的对称点N落在上,如果,则( )
A.6 B. C.2 D.
22.(2024八下·湘西期中)如图,在高为,坡面长为的楼梯表面铺地毯,地毯的长度至少需要( )
A. B. C. D.
23.(2024八下·湘西期中)下列命题的逆命题是真命题的是( )
A.若,则
B.如果两个实数相等,那么它们的绝对值相等
C.如果直角三角形的两条直角边长分别为a,b,斜边长为c,那么
D.邻补角互补.
24.(2024八下·湘西期中)在下列给出的条件中,可以判定四边形为平行四边形的条件是( )
A., B.,
C., D.,
25.(2024八下·冷水滩期中)已知直角三角形的两直角边长为3和4,则这个直角三角形的斜边长为( )
A.5 B.7 C.10 D.12
26.(2024八下·冷水滩期中)如图所示,在中,,,则的度数为( )
A. B. C. D.
27.(2024八下·冷水滩期中)中国瓷器,积淀了深厚的文化底蕴,是中国传统艺术文化的重要组成部分.瓷器上的图案设计精美,极富变化.下面瓷器图案中,既是轴对称图形又是中心对称图形的是( )
A. B.
C. D.
28.(2024八下·湖南期中)如图,在边长为的正方形中,是边的中点,是边上的一个动点(不与重合),以线段为边在正方形内作等边,是边的中点,连接,则在点运动过程中,的最小值是( )
A. B. C. D.
29.(2024八下·湖南期中)如图,将矩形纸片折叠,使边落在对角线上,折痕为,且D点落在对角线处,,,则的长为( )
A. B. C. D.
30.(2024八下·湖南期中)如图,在中,,以的三边为边向外作正方形,其面积分别为,,,,,则( )
A.9 B.12 C.15 D.144
31.(2024八下·湖南期中)在平行四边形中,用直尺和圆规作的平分线交于点,若,,则的长为( )
A. B. C. D.
32.(2024八下·湖南期中)如图,在中,,的平分线BD交AC于点D,若,则点D到AB的距离DE是( )
A.2cm B.3cm C.4cm D.5cm
33.(2024八下·湖南期中)如图,是的中位线,若,则的度数为( )
A. B. C. D.
34.(2024八下·湖南期中)如图,已知,垂足为,,,则可得到,理由是( )
A. B. C. D.
35.(2024八下·汕头期中)两条对角线相等且互相垂直平分的四边形是( )
A.平行四边形 B.矩形
C.菱形 D.正方形
36.(2024八下·祁东期中)如图, ABCD的对角线AC与BD相交于点O,∠ADB=90°,AC=10,BD=6,则AD的长是( )
A.4 B. C.8 D.2
37.(2024八下·祁东期中)已知点在第四象限内,则一次函数的图象大致是( )
A. B.
C. D.
38.(2024八下·邵东期中)小明早晨骑自行车到学校上学,匀速骑行一段时间后,发现作业本忘在家里,于是他按原路匀速返回,半路拿到爸爸送来的作业本后,为了不耽误上学的时间,决定以更快的速度匀速骑车赶往学校,则下列最能反映小明与家的距离 s ( km )与骑行时间 t ( h )之间的函数关系的大致图象是( )
A. B.
C. D.
39.(2024八下·邵东期中)如图,,,,分别是四边形四条边的中点,要使四边形为菱形,则四边形应具备的条件是( )
A.一组对边平行而另一组对边不平行
B.对角线相等
C.对角线互相平分
D.对角线互相垂直
40.(2024八下·邵东期中)下列说法正确的是 ( )
A.一组对边平行,另一组对边相等的四边形是平行四边形.
B.对角线相等的四边形是矩形.
C.矩形是轴对称图形,两条对角线所在的直线是它的对称轴.
D.对角线互相垂直平分的四边形是菱形.
41.(2024八下·邵东期中)2023年6月4日6时33分,神舟十五号载人飞船返回舱在东风着陆场平安着陆,神舟十五号载人飞行任务取得圆满成功,展现了中国航天科技的新高度.下列航天图标,其文字上方的图案是中心对称图形的是( )
A. B.
C. D.
42.(2024八下·浏阳期中)如图,在△ABC中,点D,E,F分别在边BC,AB,AC上,且DE∥CA,DF∥BA,下列说法不正确是( )
A.若AD=EF,那么四边形AEDF是矩形
B.若AD平分∠BAC,那么四边形AEDF是菱形
C.若AD⊥BC且AB=AC,那么四边形AEDF是菱形
D.若∠ADC=90°,那么四边形AEDF是矩形
43.(2024八下·浏阳期中)如图,在四边形ABCD中,∠ABC为直角,AB∥CD,AB=CD,对角线AC、BD相交于点O,AB=5,AO=6.5,则四边形ABCD的面积为( )
A.60 B.30 C.90 D.96
44.(2024八下·浏阳期中)如图,已知线段AB、AD和射线BP,且AD∥BP,在射线BP上找一点C,使得四边形ABCD是平行四边形,下列作法不一定可行的是( )
A.过点D作DC∥AB与BP交于点C
B.在AD下方作∠ADC与BP交于点C,使∠ADC=∠ABP
C.在BP上截取BC,使BC=AD,连接DC
D.以点D为圆心,AB长为半径画弧,与BP交于点C,连接DC
45.(2024八下·永兴期中)下列几组数中,能作为直角三角形三边长度的是( )
A.4,5,6 B.1,,3 C.6,8,10 D.5,12,22
46.(2024八下·永兴期中)下列图形中,是轴对称图形又是中心对称图形的是( )
A. B. C. D.
47.(2024八下·澧县期中) 如图,当秋千静止时,踏板离地的垂直高度,将它往前推至处时(即水平距离,),踏板离地的垂直高度,它的绳索始终拉直,则绳索的长是( )
A. B. C. D.
48.(2024八下·澧县期中) 如图,△ABC中,∠ACB=90°,CD是高,∠A=30°,则BD与AB的关系( )
A.BD=AB B.BD=AB C.BD=AB D.BD=AB
49.(2024八下·慈利期中)如图,在中,,,,为边上一动点,于,于,为的中点,则的最小值为
A. B. C. D.
50.(2024八下·长沙期中)如图,在正方形ABCD外取一点,连接AE,BE,DE.过点作AE的垂线交DE于点.若,.下列结论:
①;②点到直线AE的距离是;③;④.其中正确的结论个数是( )
A.4 B.3 C.2 D.1
答案解析部分
1.A
解:∵P、Q分别是AD、AC的中点,
∴CD=2PQ=4,
∴菱形ABCD的周长是4×4=16.
故答案为:A.
根据三角形的中位线定理,即可求得CD的长,进而求得菱形的周长.
2.B
3.B
4.B
解:∵点的坐标为,点的伴随点为,
∴,
∴,
∴,
∴,
∴的坐标周期变化,周期为4,
∵,
∴,
故答案为:B.
先分别计算出,,,,的坐标,得出坐标的周期为4,即可求解.
5.C
6.B
解:如图:
∵,
∴,
∴,
∵平分,平分,
∴,
∴,
∴,
∴,
∴;
故答案为:B.
证明,利用等角对等边得:,进而得到,再利用平行四边形的性质得AD长,即可得解.
7.D
8.D
9.D
10.C
11.D
12.B
13.D
14.B
15.D
16.C
解:∵四边形ABCD是平行四边形,AC=12,
∴OA=AC=6,BD=2OB,
∵AB⊥AC,AB=8,
∴OB==10,
∴BD=2OB=20.
故选C.
由四边形ABCD是平行四边形,根据平行四边形的对角线互相平分,可得OA的长,然后由AB⊥AC,AB=8,AC=12,根据勾股定理可求得OB的长,继而求得答案.
17.D
解:∵点E、F分别是AB、AC的中点,EF=4,
∴BC=2EF=8,
∵四边形ABCD是菱形,
∴AB=BC=CD=AD
∴菱形ABCD的周长是8×4=32.
故答案为:D.
由E、F分别是AB、AC的中点可知EF为△ABC的中位线,利用三角形的中位线的定理:三角形的中位线平行于三角形的第三边,且等于第三边的一半,即可求得BC的长,然后由菱形的性质:菱形的四条边都相等,即可求得菱形ABCD的周长.
18.C
解:设BN=x,由折叠的性质可得DN=AN=9-x,
∵D是BC的中点,
∴BD=3,
在Rt△NBD中,x2+32=(9-x)2,
解得x=4.
即BN=4.
故答案为:C.
设BN=x,则由折叠的性质可得DN=AN=9-x,根据中点的定义可得BD=3,在Rt△BND中,根据勾股定理可得关于x的方程,解方程即可求解.
19.C
20.C
21.C
22.A
23.C
24.B
25.A
26.A
27.B
28.A
29.D
30.D
31.C
32.C
33.B
34.A
35.D
解:根据正方形的判别方法知,两条对角线互相垂直平分的四边形是菱形,且相等又可判定为正方形,故选D.
两条对角线互相垂直平分的四边形是菱形,对角线相等的菱形是正方形,所以该四边形是正方形.
36.A
37.A
38.C
39.B
40.D
41.D
42.D
∵DE∥CA,DF∥BA,
∴ 四边形AEDF是平行四边形.
∵AD=EF,
∴ 四边形AEDF是矩形,故A正确;
∵四边形AEDF是平行四边形,AD平分∠BAC,
∴四边形AEDF是菱形,故B正确;
∵AD⊥BC且AB=AC,
∴AD平分∠BAC,
∵四边形AEDF是平行四边形,
∴四边形AEDF是菱形,故C正确;
四边形AEDF是平行四边形,∠ADC=90°,不能推出四边形AEDF是矩形,故D错误.
故答案为:D.
A利用对角线相等的平行四边形是矩形求解;B、C根据对角线平分一组对角的平行四边形是菱形求解;D添加条件∠ADC=90°,不能推出四边形AEDF是矩形.
43.A
解:∵AB=CD,AB//CD,
∴四边形ABCD是平行四边形.
∵∠ABC为直角,
∴四边形ABCD是矩形.
∵AB=5,AO=6.5,
∴AC=2AO=13,
∴BC=
∴四边形ABCD的面积为BA×BC=5×12=60.
故答案为:A.
先证明四边形ABCD是矩形,再求出BC,最后利用矩形面积公式求解.
44.D
解: ∵过点D作DC∥AB与BP交于点C ,AD∥BP,∴四边形ABCD是平行四边形(两组对边分别平行的四边形是平行四边形),故A不符合;
∵AD∥BP,∴∠A+∠B=180°,
∵在AD下方作∠ADC与BP交于点C,使∠ADC=∠B,
∴∠A+∠ADC=180°,∴AB//DC.
∵AD//BC,
∴四边形ABCD是平行四边形(两组对边分别平行的四边形是平行四边形),故B不符合;
∵AD∥BP, 在BP上截取BC,使BC=AD,连接DC ,
∴四边形ABCD是平行四边形(一组对边平行且相等的四边形是平行四边形),故C不符合;
以点D为圆心,AB长为半径画弧,与BP交于点C,连接DC , 且AD∥BP, 只满足一对边平行,另一对边相等,有可能是梯形,不一定是平行四边形,故D符合.
故答案为:D.
(1)根据两组对边分别平行的四边形是平行四边形;
(2)根据两组对边分别平行的四边形是平行四边形;
(3)根据一组对边平行且相等的四边形是平行四边形;
(4)满足一对边平行,另一对边相等不判断为平行四边形.
45.C
46.D
47.B
解:设AC=x,则AB=AC=x,AD=AB+BE-DE=x-2,
在Rt△ACD中,AC2=AD2+CD2,
∴x2=(x-2)2+42,
解得x=5,
故答案为:B.
设AC=x,则AB=AC=x,AD=x-2,在Rt△ACD中,根据勾股定理建立关于x方程并解之即可.
48.C
解:在 △ABC中,∠ACB=90°,∠A=30° , CD是高
∴AB=2BC,∠B=60°,∠BDC=90°,
∴∠BCD=90°-∠B=30°,
∴BC=2BD,
∴AB=4BD,即 BD=AB .
故答案为:C.
利用含30°角的直角三角形的性质可得AB=2BC,BC=2BD,从而得出AB=4BD,据此判断即可.
49.C
50.A
①∵∠EAB+∠BAP=90°,∠PAD+∠BAP=90°,
∴∠EAB=∠PAD,
在△APD和△AEB中,
,
∴△APD≌△AEB(SAS),
∴①正确,符合题意;
②过点B作BF⊥AE,交AE的延长线于点F,如图所示:
∵△APD≌△AEB,
∴∠APD=∠AEB,
∵∠APD+∠AEP=90°,
∴∠AEB+∠AEP=90°,
∴∠BEP=90°,
∴∠BEA+∠AEP=90°,
∵AE=AP=,
∴△AEP是等腰直角三角形,
∴∠AEP=45°,
∴∠BEA=45°,
∴△ABF是等腰直角三角形,
∵AE=,
∴由勾股定理可得:EP=2,
∵PB=3,
∴BE=1,
∴由勾股定理可得:BP=,
∴BF=BE=,
∴②正确,符合题意;
③∵∠BED=∠BEA+∠AEP=90°,
∴EB⊥ED,
∴③正确,符合题意;
④∵△APD≌△AEB,
∴PD=BE=1,
∴DE=3,
∴S正方形ABCD=AD2=AE2+DE2=,
∴④不正确,不符合题意;
综上,正确的结论是①②③,共3个,
故答案为:B.
利用正方形的性质,全等三角形的判定方法和性质,点到直线的距离公式及正方形的面积公式逐项分析判断即可.
同课章节目录
