期中真题专项复习04 证明题(含答案)--2024-2025学年七年级数学下册(苏科版2024)
文档属性
| 名称 | 期中真题专项复习04 证明题(含答案)--2024-2025学年七年级数学下册(苏科版2024) |  | |
| 格式 | docx | ||
| 文件大小 | 462.7KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-03-30 05:59:19 | ||
图片预览


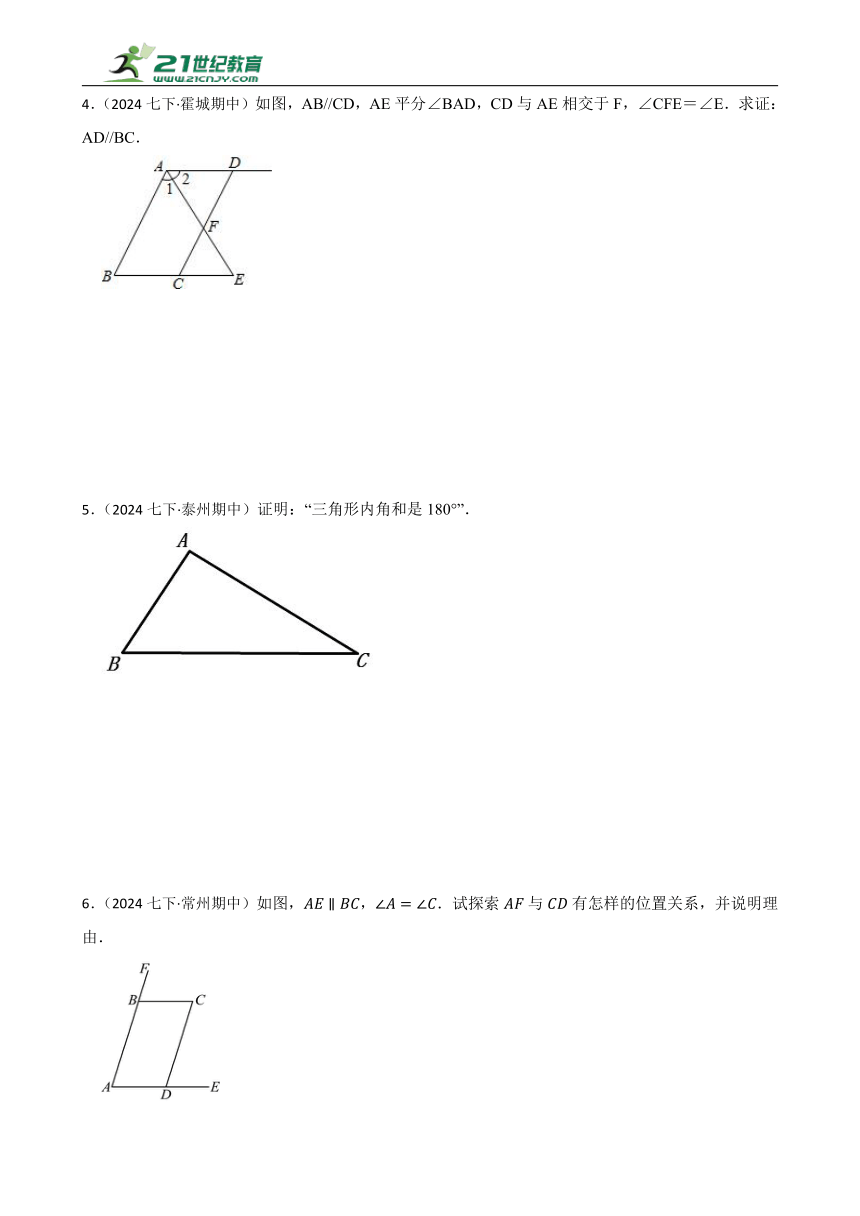

文档简介
2024-2025学年七年级数学下册(苏科版2024)
期中真题专项复习04 证明题
一、证明题
1.(2024七下·扬州期中)问题情境1:如图1,AB∥CD,P是ABCD内部一点,P在BD的右侧,探究∠B,∠P,∠D之间的关系?
小明的思路是:如图2,过P作PE∥AB,通过平行线性质,可得∠B,∠P,∠D之间满足 关系.(直接写出结论)
问题情境2
如图3,AB∥CD,P是AB,CD内部一点,P在BD的左侧,可得∠B,∠P,∠D之间满足 关系.(直接写出结论)
问题迁移:请合理的利用上面的结论解决以下问题:
已知AB∥CD,∠ABE与∠CDE两个角的角平分线相交于点F
(1)如图4,若∠E=80°,求∠BFD的度数;
(2)如图5中,∠ABM=∠ABF,∠CDM=∠CDF,写出∠M与∠E之间的数量关系并证明你的结论.
(3)若∠ABM=∠ABF,∠CDM=∠CDF,设∠E=m°,用含有n,m°的代数式直接写出∠M= .
2.(2024七下·徐州期中)如图,已知.若,,求的度数.
3.(2024七下·启东期中)已知,如图,四边形,点E为延长线上一点,点F为延长线上一点,连接,交于点G,交于点G,若,,求证:.
证明:∵(_____________),
(已知).
∴_____________=_____________(等量代换).
∴__________________________(_____________).
∴(_____________).
∵(已知),
∴(等量代换).
∴__________________________(同旁内角互补,两直线平行).
∴(_____________).
4.(2024七下·霍城期中)如图,AB//CD,AE平分∠BAD,CD与AE相交于F,∠CFE=∠E.求证:AD//BC.
5.(2024七下·泰州期中)证明:“三角形内角和是180°”.
6.(2024七下·常州期中)如图,,.试探索与有怎样的位置关系,并说明理由.
解:结论:与的位置关系是___________;
理由:∵(已知),
∴___________(_________________),
又∵(已知),
∴________(等量代换),
∴ (___________________).
7.(2024七下·江阴期中)已知,平分交射线于点E,.
(1)如图1,求证:;
(2)如图2,点F是射线上一点,过点F作交射线于点G,点N是上一点,连接,求证:;
(3)如图3,在(2)的条件下,连接,点P为延长线上一点,平分交于点M,若平分,,,求的度数.
8.(2024七下·江阴期中)如图,的平分线交于点,交的延长线于点,求证:.
请将下面的证明过程补充完整:
证明:∵(已知),
.( ① )
平分,
.( ② )
③ .(等量代换)
(已知),
∴.( ④ )
⑤ .(两直线平行,同位角相等)
.
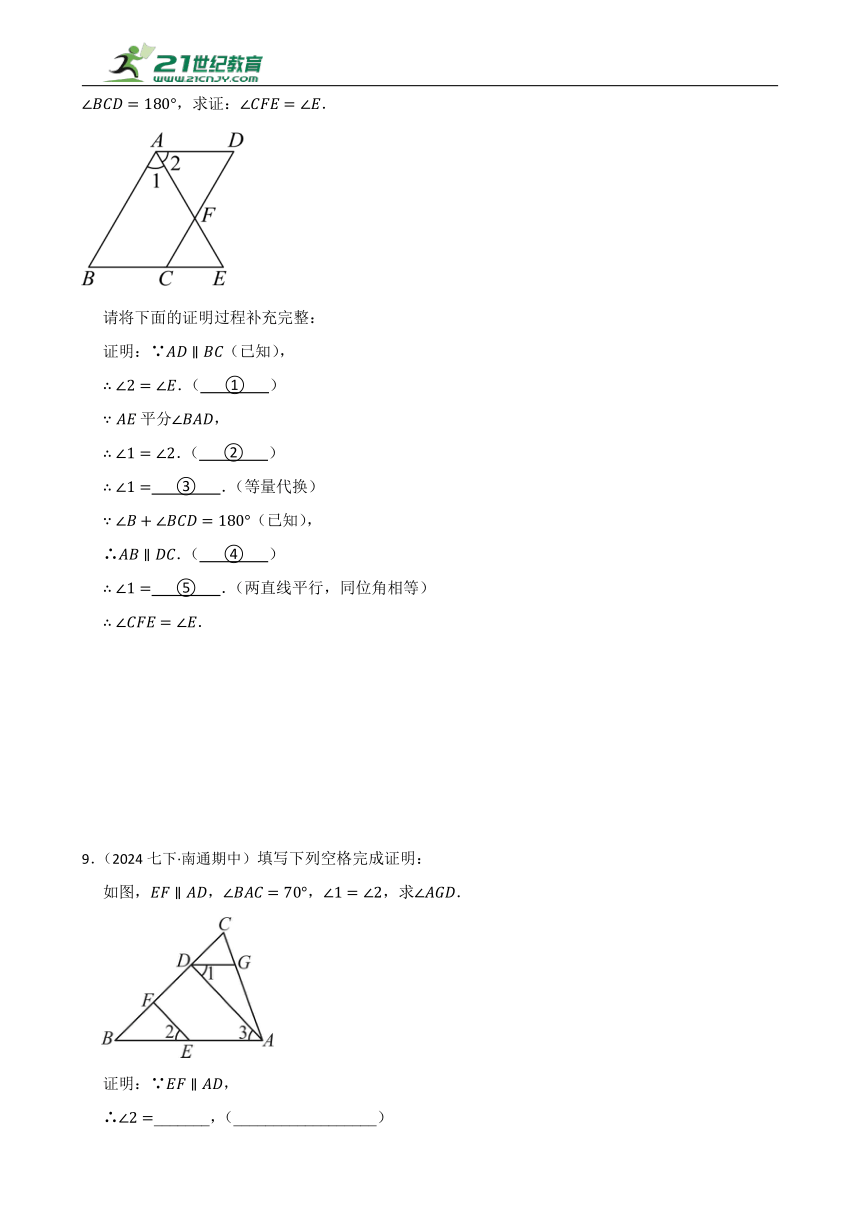
9.(2024七下·南通期中)填写下列空格完成证明:
如图,,,,求.
证明:∵,
∴_______,(__________________)
∵,
∴,
∴_____________,(___________________)
∴_______,(__________________)
∵,
∴________.
10.(2024七下·洪泽期中)如图,在中,平分交于点平分交于点,且.
(1)与有怎样的位置关系,试说明理由;
(2)若,求的度数.
11.(2024七下·盱眙期中)完成下面的证明:
如图,在四边形ABCD中,BE平分∠ABC交线段AD于点E,∠1=∠2,∠C=110°,求∠D的度数
解:∵BE平分∠ABC (已知)
∴∠2=_________( )
又∵∠1=∠2 (已知)
∴∠1=_________( )
∴AD//BC( )
∴∠C+________=180°( )
又∵∠C=110°(已知)
∴∠D=__________.
12.(2024七下·秦淮期中)如图,已知,,垂足分别为G、D,,
求证:.请你将小明的证明过程补充完整.
证明:∵,,垂足分别为G、D(已知)
∴(______),
∴(______).
∵(已证)
∴(______),
又∵(已知),
∴______,(______),
∴______,(______),
∴(______),
13.(2024七下·丰县期中)如图,,,试说明.
请补全推理过程,并在括号内填上相应的理由:
因为,,
所以(同角的补角相等).
所以________________(________).
所以________.
因为(已知),
所以________________(等量代换).
所以________________(________).
所以(________).
14.(2024七下·鼓楼期中)填空:
已知:如图,相交于点O.
求证:.
证明:在中,(______).
∴(______).
在中,同理可得
(______).
∵(______),
∴(______)
15.(2024七下·如皋期中)完成下面的证明:
如图,,垂足分别为 ,且 .求证:.
证明:(已知)
, (垂直的定义),
.
(同位角相等,两直线平行).
( )
又 (已知),
.
( )
16.(2024七下·东台期中)按图填空,并注明理由.
已知:如图,.
求证:.
证明:∵(已知),
∴ ( ).
∵(已知)
∴ .
∴( ),
∴( ).
17.(2024七下·仪征期中)【图形感知】
如图1,,点在直线上,点在直线上,点为、之间一点.
(1)如图2,该基本图形称为“铅笔头型”(实线部分),它有一个常用数学结论:,它可以通过如下方法证明,请你帮忙完成该结论的推理过程.
证明:如图①,过点作,
∵,(已知),
∴_________(平行于同一条直线的两条直线平行),
∴,,
∴(等式性质)
∴.
(2)如图3,该基本图形称为“型”(实线部分),仿照上面结论的推理思路可得、、之间的关系是________;
【结论应用】直接利用上述结论进行证明;
(3)如图4,直线,点,在直线上,点,在直线上,直线,分别平分,,且交于点.猜想并证明与的数量关系.
【拓展延伸】
(4)如图5,已知,与两个角的角平分线相交于点.
若,,设,________.(用含有,的代数式表示)
18.(2024七下·铜山期中)如图,已知,平分,平分,请说明的理由.
解:∵( ),
∴( ).
∵平分,平分(已知),
∴,∠ ( ),
∴∠ ∠ ,( )
∴( ).
19.(2024七下·玄武期中)把下面的证明补充完整.
已知:如图,在四边形中,,,平分,交于点,平分,交于点.求证:.
证明:平分,
(______),
平分,
,
______(等量代换)
(已知),
(______),
______,
.
20.(2024七下·阜宁期中)如图,于D,点F是上任意一点,于E,且,.
(1)求证:;
请补全解答过程,即在横线处填上结论或理由.
证明:∵,,(已知)
∴ ,(垂直于同一直线的两直线平行)
∴,( )
又∵,(已知)
∴,(等量代换)
∴ ,( )
∴,( )
(2)若平分,求的度数.
21.(2024七下·吴江期中)如图,在△ABC中,AD平分∠BAC,P为线段AD上的一个动点,PE⊥AD交直线BC于点E.
(1)若∠B=30°,∠ACB=80°,求∠E的度数;
(2)当P点在线段AD上运动时,猜想∠E与∠B、∠ACB的数量关系,写出结论无需证明.
答案解析部分
1.问题情境1:∠B+∠BPD+∠D=360°,∠P=∠B+∠D;(1)140°;(2)∠E+∠M=60°(3)
2.
3.对顶角相等;;;;;同位角相等;两直线平行;两直线平行,同旁内角互补;;;两直线平行,内错角相等
4.解:∵ AB//CD,
,
平分 ,
,
,
,
∴ AD//BC .
由二直线平行,同位角相等,得,由角平分线的定义可得 , 结合∠CFE=∠E可得,根据内错角相等,两直线平行,即证.
5.解:如图,过A点作,
∠MAB=∠B,∠NAC=∠C,(两直线平行,内错角相等)
∠BAC+∠B+∠C=∠MAB+∠BAC+∠NAC=180°.
过A点作,根据直线平行性质可得∠MAB=∠B,∠NAC=∠C,再根据平角性质进行角之间的转换即可求出答案.
6.;;两直线平行,内错角相等;;;同位角相等,两直线平行
7.(1)证明:∵平分,
∴,
∵,
∴,
∴;
(2)证明:过点E作,交AD于点H,如图所示
∵,
∴
∴,
又∵,
∴,
又∵,
∴;
(3)解:设,
∵平分,
∴,
∴,
∴,
∵,
∴,
∵,
∴,
由(2)得:,
即90°=4α+∠ENG
∴,
∵平分,
∴,
∴,
∴,
∴,
∵,
即,解得:,
∴,
∴=.
(1)利用平分 ,推出,继而可得,即可证明;
(2)过点E作,可知,可得,,继而可知,由,可证得结论;
(3)设,分别表示出,,继而可得,即可推出,再利用,以及(2)中的结论可得,可推出,从而可得,,,再根据已知,列出关于α的方程,即可求出α的度数,继而求出的度数 .
8.证明:∵(已知),
.(两直线平行,内错角相等)
平分,
.(角平分线的定义)
.(等量代换)
(已知),
∴.(同旁内角互补,两直线平行)
.(两直线平行,同位角相等)
.
故答案为:两直线平行,内错角相等;角平分线的定义;;同旁内角互补,两直线平行;.
根据,推出,结合题目所给条件 平分∠BAD,推出∠1=∠2,继而得到,在根据,得到,则,等角代换后即可求证.
9.;两直线平行,同位角相等;;;内错角相等,两直线平行;;
10.(1)
(2)
11.;角平分线的性质;;等量代换;内错角相等,两直线平行;;两直线平行,同旁内角互补;70°
12.垂直定义,同位角相等;两直线平行,两直线平行;同位角相等;,等量代换;;内错角相等,两直线平行;两直线平行,同旁内角互补.
13.;;内错角相等,两直线平行;;;;;;同位角相等,两直线平行;两直线平行,同位角相等
14.三角形的内角和等于,等式的性质,,对顶角相等,等量代换.
15.90;90;;两直线平行,同位角相等;内错角相等,两直线平行
16.,两直线平行,同位角相等; ;;内错角相等,两直线平行;两直线平行,同位角相等
17.(1);(2);(3);(4)
18.已知;两直线平行,内错角相等;;角平分线定义;;;等量代换;内错角相等,两直线平行
19.角平分线定义;;两直线平行,内错角相等;
20.(1):两直线平行,同位角相等:;内错角相等,两直线平行;两直线平行,同位角相等
(2)
21.(1)∠E=25°;(2)∠E=(∠ACB﹣∠B).
期中真题专项复习04 证明题
一、证明题
1.(2024七下·扬州期中)问题情境1:如图1,AB∥CD,P是ABCD内部一点,P在BD的右侧,探究∠B,∠P,∠D之间的关系?
小明的思路是:如图2,过P作PE∥AB,通过平行线性质,可得∠B,∠P,∠D之间满足 关系.(直接写出结论)
问题情境2
如图3,AB∥CD,P是AB,CD内部一点,P在BD的左侧,可得∠B,∠P,∠D之间满足 关系.(直接写出结论)
问题迁移:请合理的利用上面的结论解决以下问题:
已知AB∥CD,∠ABE与∠CDE两个角的角平分线相交于点F
(1)如图4,若∠E=80°,求∠BFD的度数;
(2)如图5中,∠ABM=∠ABF,∠CDM=∠CDF,写出∠M与∠E之间的数量关系并证明你的结论.
(3)若∠ABM=∠ABF,∠CDM=∠CDF,设∠E=m°,用含有n,m°的代数式直接写出∠M= .
2.(2024七下·徐州期中)如图,已知.若,,求的度数.
3.(2024七下·启东期中)已知,如图,四边形,点E为延长线上一点,点F为延长线上一点,连接,交于点G,交于点G,若,,求证:.
证明:∵(_____________),
(已知).
∴_____________=_____________(等量代换).
∴__________________________(_____________).
∴(_____________).
∵(已知),
∴(等量代换).
∴__________________________(同旁内角互补,两直线平行).
∴(_____________).
4.(2024七下·霍城期中)如图,AB//CD,AE平分∠BAD,CD与AE相交于F,∠CFE=∠E.求证:AD//BC.
5.(2024七下·泰州期中)证明:“三角形内角和是180°”.
6.(2024七下·常州期中)如图,,.试探索与有怎样的位置关系,并说明理由.
解:结论:与的位置关系是___________;
理由:∵(已知),
∴___________(_________________),
又∵(已知),
∴________(等量代换),
∴ (___________________).
7.(2024七下·江阴期中)已知,平分交射线于点E,.
(1)如图1,求证:;
(2)如图2,点F是射线上一点,过点F作交射线于点G,点N是上一点,连接,求证:;
(3)如图3,在(2)的条件下,连接,点P为延长线上一点,平分交于点M,若平分,,,求的度数.
8.(2024七下·江阴期中)如图,的平分线交于点,交的延长线于点,求证:.
请将下面的证明过程补充完整:
证明:∵(已知),
.( ① )
平分,
.( ② )
③ .(等量代换)
(已知),
∴.( ④ )
⑤ .(两直线平行,同位角相等)
.
9.(2024七下·南通期中)填写下列空格完成证明:
如图,,,,求.
证明:∵,
∴_______,(__________________)
∵,
∴,
∴_____________,(___________________)
∴_______,(__________________)
∵,
∴________.
10.(2024七下·洪泽期中)如图,在中,平分交于点平分交于点,且.
(1)与有怎样的位置关系,试说明理由;
(2)若,求的度数.
11.(2024七下·盱眙期中)完成下面的证明:
如图,在四边形ABCD中,BE平分∠ABC交线段AD于点E,∠1=∠2,∠C=110°,求∠D的度数
解:∵BE平分∠ABC (已知)
∴∠2=_________( )
又∵∠1=∠2 (已知)
∴∠1=_________( )
∴AD//BC( )
∴∠C+________=180°( )
又∵∠C=110°(已知)
∴∠D=__________.
12.(2024七下·秦淮期中)如图,已知,,垂足分别为G、D,,
求证:.请你将小明的证明过程补充完整.
证明:∵,,垂足分别为G、D(已知)
∴(______),
∴(______).
∵(已证)
∴(______),
又∵(已知),
∴______,(______),
∴______,(______),
∴(______),
13.(2024七下·丰县期中)如图,,,试说明.
请补全推理过程,并在括号内填上相应的理由:
因为,,
所以(同角的补角相等).
所以________________(________).
所以________.
因为(已知),
所以________________(等量代换).
所以________________(________).
所以(________).
14.(2024七下·鼓楼期中)填空:
已知:如图,相交于点O.
求证:.
证明:在中,(______).
∴(______).
在中,同理可得
(______).
∵(______),
∴(______)
15.(2024七下·如皋期中)完成下面的证明:
如图,,垂足分别为 ,且 .求证:.
证明:(已知)
, (垂直的定义),
.
(同位角相等,两直线平行).
( )
又 (已知),
.
( )
16.(2024七下·东台期中)按图填空,并注明理由.
已知:如图,.
求证:.
证明:∵(已知),
∴ ( ).
∵(已知)
∴ .
∴( ),
∴( ).
17.(2024七下·仪征期中)【图形感知】
如图1,,点在直线上,点在直线上,点为、之间一点.
(1)如图2,该基本图形称为“铅笔头型”(实线部分),它有一个常用数学结论:,它可以通过如下方法证明,请你帮忙完成该结论的推理过程.
证明:如图①,过点作,
∵,(已知),
∴_________(平行于同一条直线的两条直线平行),
∴,,
∴(等式性质)
∴.
(2)如图3,该基本图形称为“型”(实线部分),仿照上面结论的推理思路可得、、之间的关系是________;
【结论应用】直接利用上述结论进行证明;
(3)如图4,直线,点,在直线上,点,在直线上,直线,分别平分,,且交于点.猜想并证明与的数量关系.
【拓展延伸】
(4)如图5,已知,与两个角的角平分线相交于点.
若,,设,________.(用含有,的代数式表示)
18.(2024七下·铜山期中)如图,已知,平分,平分,请说明的理由.
解:∵( ),
∴( ).
∵平分,平分(已知),
∴,∠ ( ),
∴∠ ∠ ,( )
∴( ).
19.(2024七下·玄武期中)把下面的证明补充完整.
已知:如图,在四边形中,,,平分,交于点,平分,交于点.求证:.
证明:平分,
(______),
平分,
,
______(等量代换)
(已知),
(______),
______,
.
20.(2024七下·阜宁期中)如图,于D,点F是上任意一点,于E,且,.
(1)求证:;
请补全解答过程,即在横线处填上结论或理由.
证明:∵,,(已知)
∴ ,(垂直于同一直线的两直线平行)
∴,( )
又∵,(已知)
∴,(等量代换)
∴ ,( )
∴,( )
(2)若平分,求的度数.
21.(2024七下·吴江期中)如图,在△ABC中,AD平分∠BAC,P为线段AD上的一个动点,PE⊥AD交直线BC于点E.
(1)若∠B=30°,∠ACB=80°,求∠E的度数;
(2)当P点在线段AD上运动时,猜想∠E与∠B、∠ACB的数量关系,写出结论无需证明.
答案解析部分
1.问题情境1:∠B+∠BPD+∠D=360°,∠P=∠B+∠D;(1)140°;(2)∠E+∠M=60°(3)
2.
3.对顶角相等;;;;;同位角相等;两直线平行;两直线平行,同旁内角互补;;;两直线平行,内错角相等
4.解:∵ AB//CD,
,
平分 ,
,
,
,
∴ AD//BC .
由二直线平行,同位角相等,得,由角平分线的定义可得 , 结合∠CFE=∠E可得,根据内错角相等,两直线平行,即证.
5.解:如图,过A点作,
∠MAB=∠B,∠NAC=∠C,(两直线平行,内错角相等)
∠BAC+∠B+∠C=∠MAB+∠BAC+∠NAC=180°.
过A点作,根据直线平行性质可得∠MAB=∠B,∠NAC=∠C,再根据平角性质进行角之间的转换即可求出答案.
6.;;两直线平行,内错角相等;;;同位角相等,两直线平行
7.(1)证明:∵平分,
∴,
∵,
∴,
∴;
(2)证明:过点E作,交AD于点H,如图所示
∵,
∴
∴,
又∵,
∴,
又∵,
∴;
(3)解:设,
∵平分,
∴,
∴,
∴,
∵,
∴,
∵,
∴,
由(2)得:,
即90°=4α+∠ENG
∴,
∵平分,
∴,
∴,
∴,
∴,
∵,
即,解得:,
∴,
∴=.
(1)利用平分 ,推出,继而可得,即可证明;
(2)过点E作,可知,可得,,继而可知,由,可证得结论;
(3)设,分别表示出,,继而可得,即可推出,再利用,以及(2)中的结论可得,可推出,从而可得,,,再根据已知,列出关于α的方程,即可求出α的度数,继而求出的度数 .
8.证明:∵(已知),
.(两直线平行,内错角相等)
平分,
.(角平分线的定义)
.(等量代换)
(已知),
∴.(同旁内角互补,两直线平行)
.(两直线平行,同位角相等)
.
故答案为:两直线平行,内错角相等;角平分线的定义;;同旁内角互补,两直线平行;.
根据,推出,结合题目所给条件 平分∠BAD,推出∠1=∠2,继而得到,在根据,得到,则,等角代换后即可求证.
9.;两直线平行,同位角相等;;;内错角相等,两直线平行;;
10.(1)
(2)
11.;角平分线的性质;;等量代换;内错角相等,两直线平行;;两直线平行,同旁内角互补;70°
12.垂直定义,同位角相等;两直线平行,两直线平行;同位角相等;,等量代换;;内错角相等,两直线平行;两直线平行,同旁内角互补.
13.;;内错角相等,两直线平行;;;;;;同位角相等,两直线平行;两直线平行,同位角相等
14.三角形的内角和等于,等式的性质,,对顶角相等,等量代换.
15.90;90;;两直线平行,同位角相等;内错角相等,两直线平行
16.,两直线平行,同位角相等; ;;内错角相等,两直线平行;两直线平行,同位角相等
17.(1);(2);(3);(4)
18.已知;两直线平行,内错角相等;;角平分线定义;;;等量代换;内错角相等,两直线平行
19.角平分线定义;;两直线平行,内错角相等;
20.(1):两直线平行,同位角相等:;内错角相等,两直线平行;两直线平行,同位角相等
(2)
21.(1)∠E=25°;(2)∠E=(∠ACB﹣∠B).
同课章节目录
