期中真题专项复习05 解答题(含答案)--2024-2025学年七年级数学下册(苏科版2024)
文档属性
| 名称 | 期中真题专项复习05 解答题(含答案)--2024-2025学年七年级数学下册(苏科版2024) |  | |
| 格式 | docx | ||
| 文件大小 | 842.9KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-03-30 06:05:02 | ||
图片预览



文档简介
2024-2025学年七年级数学下册(苏科版2024)
期中真题专项复习05解答题
一、解答题
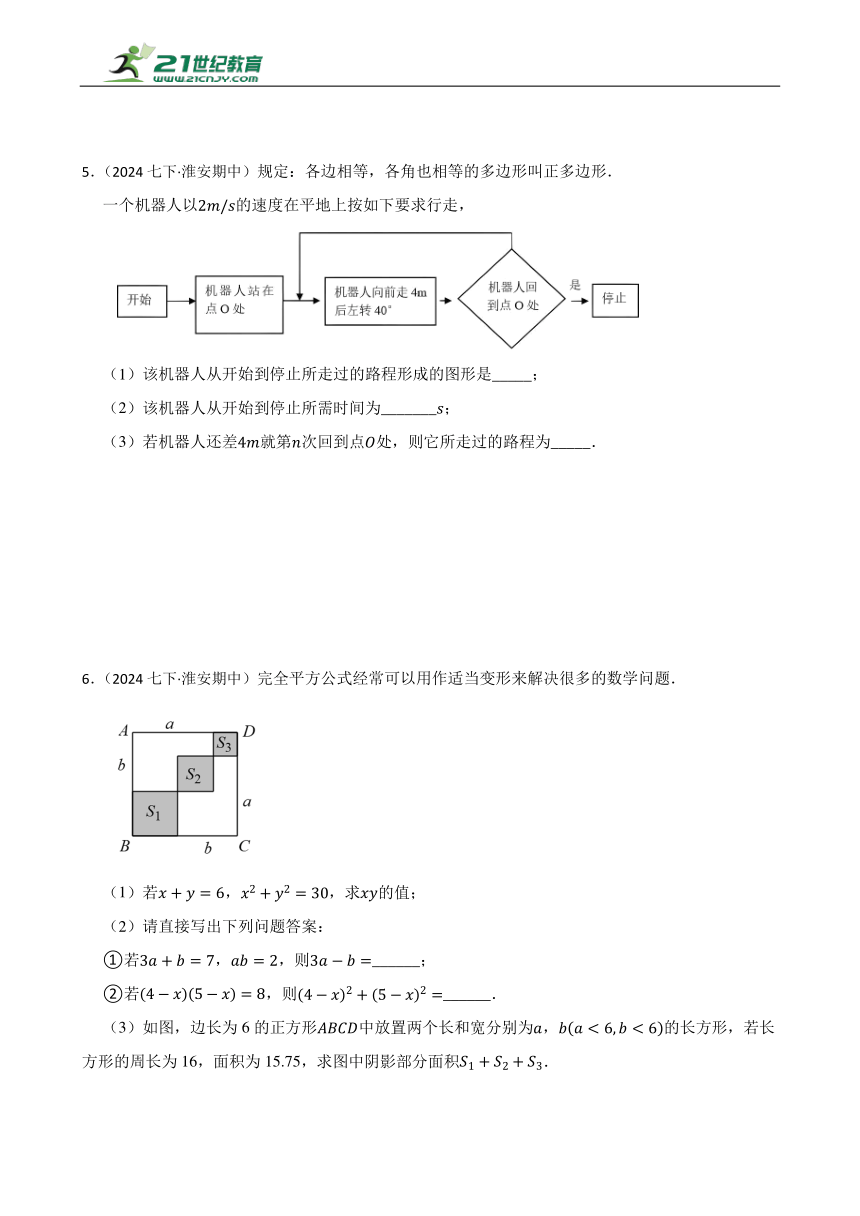
1.(2024七下·淮安期中)【观察】如图①是一个长为、宽为b的长方形,沿图中虚线用剪刀平均分成四块小长方形,然后用四块小长方形拼成一个大正方形,如图②所示,请直接写出,,之间的等量关系____________________________;
【应用】若,,则_______________;
【拓展】如图③,正方形的边长为x,,,长方形的面积是200,四边形和四边形都是正方形,四边形是长方形,求图中阴影部分的面积.
2.(2024七下·盐城期中)教科书中这样写道:“我们把多项式及叫做完全平方式”,如果一个多项式不是完全平方式,我们常做如下变形:先添加一个适当的项,使式子中出现完全平方式,再减去这个项,使整个式子的值不变,这种方法叫做配方法.配方法是一种重要的解决问题的数学方法,不仅可以将一个看似不能分解的多项式分解因式,还能解决一些与非负数有关的问题或求代数式最大值,最小值等.
例如:分解因式
;
例如:求代数式的最小值为.可知当时,有最小值,最小值是,根据阅读材料用配方法解决下列问题:
(1)分解因式:______;
(2)当a为何值时,多项式有最大值,并求出这个最大值;
(3)当a,b为何值时,多项式有最小值,并求出这个最小值.
3.(2024七下·徐州期中)如图,已知,求的度数.
4.(2024七下·南京期中)(1)已知,求的值;
(2)已知,,求:
①的值;
②的值.
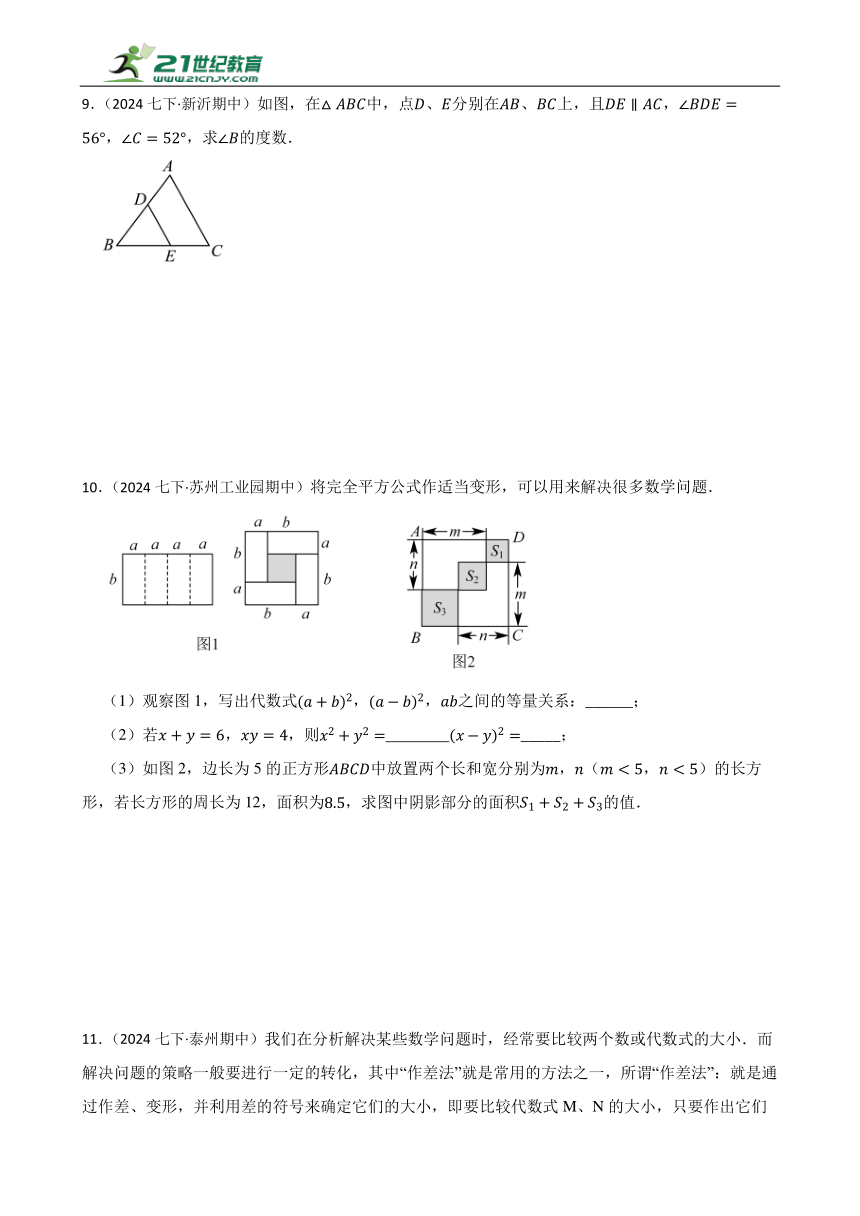
5.(2024七下·淮安期中)规定:各边相等,各角也相等的多边形叫正多边形.
一个机器人以的速度在平地上按如下要求行走,
(1)该机器人从开始到停止所走过的路程形成的图形是_____;
(2)该机器人从开始到停止所需时间为_______;
(3)若机器人还差就第次回到点处,则它所走过的路程为_____.
6.(2024七下·淮安期中)完全平方公式经常可以用作适当变形来解决很多的数学问题.
(1)若,,求的值;
(2)请直接写出下列问题答案:
①若,,则______;
②若,则______.
(3)如图,边长为6的正方形中放置两个长和宽分别为,的长方形,若长方形的周长为16,面积为15.75,求图中阴影部分面积.
7.(2024七下·淮安期中)已知,,
求①的值;②的值.
8.(2024七下·新沂期中)如图,在中.
(1)如图1,若,与的平分线交于点.求的度数;
(2)如图2,若,的外角与的平分线交于点.求的度数(用来表示);
(3)如图3,的等分线()与外角的等分线()交于点,若,,则 .
9.(2024七下·新沂期中)如图,在中,点、分别在、上,且,,,求的度数.
10.(2024七下·苏州工业园期中)将完全平方公式作适当变形,可以用来解决很多数学问题.
(1)观察图1,写出代数式,,之间的等量关系:______;
(2)若,,则 _____;
(3)如图2,边长为5的正方形中放置两个长和宽分别为,(,)的长方形,若长方形的周长为12,面积为,求图中阴影部分的面积的值.
11.(2024七下·泰州期中)我们在分析解决某些数学问题时,经常要比较两个数或代数式的大小.而解决问题的策略一般要进行一定的转化,其中“作差法”就是常用的方法之一,所谓“作差法”:就是通过作差、变形,并利用差的符号来确定它们的大小,即要比较代数式M、N的大小,只要作出它们的差,若,则;若,则.若,则,
请你用“作差法”解决以下问题:
(1)如图,试比较图①、图②两个矩形的周长的大小.
(2)如图③,把边长为的大正方形分割成两个边长分别是a、b的小正方形及两个矩形,试比较两个小正方形的面积之和与两个矩形面积之和的大小.
12.(2024七下·江阴期中)对于平面内的∠M和∠N,若存在一个常数k>0,使得∠M+k∠N=360°,则称∠N为∠M的k系补周角.如若∠M=90°,∠N=45°,则∠N为∠M的6系补周角.
(1)若∠H=120°,则∠H的4系补周角的度数为 °;
(2)在平面内AB∥CD,点E是平面内一点,连接BE,DE;
①如图1,∠D=60°,若∠B是∠E的3系补周角,求∠B的度数;
②如图2,∠ABE和∠CDE均为钝角,点F在点E的右侧,且满足∠ABF=n∠ABE,∠CDF=n∠CDE(其中n为常数且n>1),点P是∠ABE角平分线BG上的一个动点,在P点运动过程中,请你确定一个点P的位置,使得∠BPD是∠F的k系补周角,并直接写出此时的k值(用含n的式子表示).
13.(2024七下·江阴期中)如图,是的高,是的角平分线,F是中点,.
(1)求的度数;
(2)若与的周长差为3,,则 .
14.(2024七下·扬州期中)(1)若,求的值.
(2)已知,,求的值.
15.(2024七下·宿城期中)如图,是一个正方体的展开图,标注字母“a”的面是正方体的正面,如果正方体相对两个面上的代数式的值相等,试求代数式(2x﹣y)(2x+y)﹣(2x﹣y)2的值.
16.(2024七下·秦安期中)某铁件加工厂用如图1的长方形和正方形铁片(长方形的宽与正方形的边长相等)加工成如图2的竖式与横式两种无盖的长方体铁容器.(加工时接缝材料不计)
(1)如果加工竖式铁容器与横式铁容器各1个,则共需要长方形铁片 张,正方形铁片 张.
(2)现有长方形铁片2014张,正方形铁片1176张,如果加工成这两种铁容器,刚好铁片全部用完,那么加工的竖式铁容器、横式铁容器各有多少个
(3)把长方体铁容器加盖可以加工成为铁盒.现用35张铁板做成与如图相同的长方形铁片和正方形铁片,已知每张铁板可做成3个长方形铁片或4个正方形铁片,也可以将一张铁板做成1个长方形铁片和2个正方形铁片.该如何充分利用这些铁板加工成铁盒,最多可以加工成多少个铁盒
17.(2024七下·泰州期中)解二元一次方程组:
18.(2024七下·宝安期中)如图1,有A型,B型正方形卡片和C型长方形卡片各若干张.
(1)用1张A型卡片,2张B型卡片,3张C型卡片拼成一个长方形,如图2,用两种方法计算这个长方形面积,可以得到一个等式:__________________________;
(2)选取1张B型卡片,6张C型卡片,__________张A型卡片,可以拼成一个正方形,这个正方形的边长用含a,b的式子表示为__________;
(3)如图3,在长方形中,分别为上一点,且,在左侧放置1张A型卡片,在下方放置一张B型卡片.若图中的长方形的面积为8,求一张A型卡片和一张B型卡片面积之和.
19.(2024七下·鼓楼期中)如图①所示,在中,若,则称,分别为的“三分线”.其中,是“邻三分线”,是“邻三分线”.
(1)如图②,在中,,,若的邻三分线交于点,则________;
(2)如图③,在中,是的邻三分线,是的邻三分线,若,求的度数;
(3)在中,是的外角,的三分线与的邻三分线交于点.若,,直接写出的度数.(用含、的代数式表示)
20.(2023七下·中江期中)如图①,在平面直角坐标系中,,,且满足,过作轴于.
(1)求三角形的面积;
(2)如图②,若过作交轴于,且,分别平分,,求的度数;
(3)在轴上是否存在点,使得三角形和三角形的面积相等?若存在,求出点的坐标;若不存在,请说明理由.
21.(2024七下·如东期中)在等式中,当时,;当时,;当与时,的值相等.求,,的值.
22.(2024七下·盐城期中)如图,用4个长是a,宽是b的长方形拼成了一个如图2所示的“回形”正方形.
(1)拼图前后,请写出所用图形(4个长方形)的面积的计算方法:拼图前: ;拼图后: ;因为拼图前后的面积不变,所以可得恒等式: ;
(2)利用(1)中得到的恒等式,解决下面的问题:已知,,求的值.
23.(2024七下·盐城期中)如图,是的高,,,求的度数.
24.(2024七下·昆山期中)根据下列条件回答问题
(1)已知,求n的值;
(2)已知,,求的值.
25.(2024七下·昆山期中)如图,在中,平分交于点,是的高,与交于点.若,,求的度数.
26.(2024七下·淮阴期中)【结论发现】
小明在完成教材第43页第21题后发现:三角形的一个内角平分线与另一内角的外角平分线的夹角的度数是三角形第三内角度数的一半.
【结论应用】
(1)如图1,在中,,点E是的内角平分线与外角平分线的交点,则的度数为 °;
(2)如图2,在中,,延长至点E,延长至点D,已知、的角平分线与的角平分线及其反向延长线交于P、F,求的度数;
【拓展延伸】
(3)如图3,四边形的内角与外角的平分线形成如图所示形状.
①已知,,求的度数;
②直接写出与的数量关系.
27.(2024七下·苏州工业园期中)如图,在中,,是线段延长线上的动点,在线段上取一点,使.
(1)当点在线段上时,且,求的度数;
(2)若,且是直角三角形,则______
28.(2024七下·苏州工业园期中)已知:,,求下列各式的值:
(1);
(2);
(3).
29.(2024七下·南京期中)如图,已知长方形中,,,点是的中点,点从点出发在上以每秒的速度向点运动,运动时间设为1秒.(假定)
(1)当秒时,求阴影部分(即三角形)的面积;
(2)用含的式子表示阴影部分的面积;
(3)过点作交于点,过点作交于点,请直接写出在点运动过程中,和的数量关系.
30.(2024七下·海安期中)已知关于 x,y 的二元一次方程组 的解满足.
(1)求 k 的取值范围;
(2)在 (1) 的条件下,若不等式的解为,请写出符合条件的 k 的整数值.
31.(2024七下·江阴期中)已知,平分,点,,分别是射线,,上的动点,,不与点重合),连接,连接交射线于点,设.
(1)如图1,若,
①的度数是 ;
②当时,的度数是 ;当时,的度数是 ;
(2)在一个四边形中,若存在一个内角是它的对角的2倍,我们称这样的四边形为“完美四边形”,如图2,若,延长交射线于点,当四边形为“完美四边形”时,求的值.
32.(2024七下·江阴期中)2002年8月,在北京召开的国际数学家大会会标取材于我国古代数学家赵爽发现的“弦图”,它是由四个大小相等,形状相同的直角三角形与中间的小正方形拼 成的一个大正方形(如图1),设直角三角形的较短直角边为a,较长直角边为b,最长的斜边为c.
(1)若,则图1中大正方形的面积为 ;
(2)猜想之间的数量关系,并按给出的格式说明理由.
∵ , = ,
∴ ;
(3)若图1中大正方形的面积是15,小正方形的面积是1,现将四个直角三角形按如图 2的形式重新摆放,那么图2中最大的正方形的面积为 .
33.(2024七下·江阴期中)因式分解:
(1) (2) x3﹣9x; (3)x3y﹣10x2y+25xy
34.(2024七下·锡山期中)[知识生成]
(1)通常,用两种不同的方法计算同一个图形的面积,可以得到一个恒等式.
如图1,有四张长为、宽为的长方形纸片按如图方式拼成了一个正方形,请你通过拼图写出、、之间的等量关系是______.
[知识应用]
(2)若,,求的值;
[知识迁移]
(3)如图2,为创办文明校园,美化校园环境,某校计划要在面积为的长方形空地中划出长方形和长方形,两个长方形重合部分刚好建一个长为,宽为的喷泉水池,现将图中阴影部分区域作为花圃,且花圃总周长为,则的长度为多少米?
35.(2024七下·邳州期中)阅读材料:已知,,求的值.
解:.
参考上面的方法求解下列问题:
(1)已知满足,求的值;
(2)如图①,已知长方形的周长为14,分别以为边,向外作正方形,且正方形的面积和为31.
①求长方形的面积;
②如图②,连接,求的面积.
36.(2024七下·邳州期中)如图,是的中线,是的高,,,,.
(1)求高的长;
(2)求的面积.
37.(2024七下·无锡期中)如图,在中,,,D是边上一点,将沿过点D的直线折叠,使点B落在下方的点F处,折痕交于点E.
(1)当时,求的度数;
(2)当的一边与平行时,求的度数.
38.(2024七下·无锡期中)如图,在中,点D、G分别在边、上,点E、F在边上,且,,.
(1)求的度数;
(2)若,求的度数.
39.(2024七下·南京期中)在课后服务课上,老师准备了若干个如图1的三种纸片,A种纸片是边长为a的正方形,B种纸片是边长为b的正方形,C种纸片是长为b,宽为a的长方形,并用A种纸片一张,B种纸片一张,C种纸片两张拼成如图2的大正方形.
(1)根据图2,写出一个我们熟悉的数学公式 .
(2)根据(1)中的数学公式,解决如下问题:
①已知:a+b=7,a2+b2=25,求ab的值.
②如果一个长方形的长和宽分别为(8﹣x)和(x﹣2),且(8﹣x)2+(x﹣2)2=20,求这个长方形的面积.
40.(2024七下·苏州期中)小明在学习配方法时,将关于x的多项式配方成,发现当取任意一对互为相反数的数时,多项式的值是相等的.例如:当时,即或-1时,的值均为6;当时,即或-2时,的值均为11.于是小明给出一个定义:对于关于x的多项式,若当取任意一对互为相反数的数时,该多项式的值相等,就称该多项式关于对偶,例如关于对偶.
请你结合小明的思考过程,运用此定义解决下列问题:
(1)多项式关于__________对偶;
(2)当或时,关于x的多项的值相等,求b的值;
(3)若整式)关于对偶,求n的值.
41.(2024七下·苏州期中)如图,将一张大长方形纸板按图中虚线裁剪成9块,其中有2块是边长为a厘米的大正方形,2块是边长都为b厘米的小正方形,5块是长为a厘米,宽为b厘米的相同的小长方形,且.
(1)观察图形,可以发现代数式可以因式分解为______.
(2)若图中空白部分的面积为20平方厘米,大长方形纸板的周长为30厘米,求图中阴影部分的面积.
42.(2024七下·苏州期中)如图,已知,且,求的度数.
43.(2024七下·鼓楼期中)已知,在中,,,,是射线,上的点,连接.分别过,作,外角的角平分线相交于点.
(1)如图1,点,在线段,延长线上,若,求.
(2)如图2,点在线段延长线上,点在线段上,与相交于点.若,求.
(3)如图3,点在线段上运动(不与,重合),点在线段的延长线上运动,请直接写出的取值范围.
44.(2024七下·泗洪期中)根据完全平方公式,把形如的二次三项式(或其一部分)配成完全平方式的方法叫做“配方法”.例如把配方如下:.请完成下列问题:
(1)填空:配方多项式的结果为 ;
(2)当等于多少时,代数式的值最小?
(3)用一根长为米的绳子围成一个长方形,请问长方形的边长为多少时,围成的长方形面积最大?最大面积是多少?
45.(2024七下·南京期中)如果三角形中任意两个内角与满足,那么我们称这样的三角形为“准直角三角形”
(1)在中,若,,则______“准直角三角形”(填写是或不是);
(2)如果是“准直角三角形”,那么是______,(从下列四个选项中选择,填写符合条件的序号)(①锐角三角形;②直角三角形;③钝角三角形;④都有可能),请说明理由;
(3)如图,在中,,,平分交于点.
①若交于点,在①,②,③,④中“准直角三角形”是______(填写序号);
②在直线上取一点,当是“准直角三角形”时,直接写出的度数.
46.(2024七下·扬州期中)已知,当时,y的值为2,当时,y的值为14.
(1)求p,q的值;
(2)求时,y的值.
47.(2024七下·南京期中)分解因式:
(1);
(2).
48.(2024七下·南京期中)如图,在中,是的高,平分,若.求的度数.
49.(2024七下·盐城期中)因式分解:
(1);
(2).
50.(2024七下·钟楼期中)如图,将两个完全相同的直角三角板、放置在一起,点B、D重合,点F在上,与交于点G.已知,.
(1)_____________________°;
(2)现将图中的绕点F按每秒的速度沿逆时针方向旋转一定角度,旋转时间为t秒,在旋转的过程中,当恰有一边与平行时,请直接写出t的值.
答案解析部分
1.观察:;应用:;拓展:900
2.(1);
(2)2,22;
(3),,20.
3.
4.(1);(2)①;②
5.(1)正九边形;
(2)18;
(3).
6.(1)3
(2)①② 17
(3)12.5
7.①6;②
8.(1)
(2)
(3)4
9.
10.(1)
(2)28,20
(3)
11.(1)
(2)
12.(1)60
(2)①∠B=75°,②当BG上的动点P为∠CDE的角平分线与BG的交点时,满足∠BPD是∠F的k系补周角,此时k=2n.
13.(1)
(2)10
14.(1)16;(2)
15.-40
16.(1)共需要长方形铁片7张,正方形铁片3张;(2)加工的竖式容器有100个,横式容器有539个;(3)最多可做19个.
17.
18.(1)
(2)9,
(3)一张A型卡片和一张B型卡片面积之和为20
19.(1)
(2)
(3)当是“邻三分线”时,;当是“邻三分线”时,
20.(1)4
(2)
(3)存在,点的坐标为或
21.
22.(1);;
(2)
23.
24.(1)
(2)25
25.
26.(1)20;(2);(3)①;②
27.(1)
(2)或
28.(1)100
(2)4
(3)
29.(1)22.5
(2)
(3)
30.(1)
(2) ,
31.(1)①;②,
(2)的值是或或
32.(1)100
(2),;;
(3)29
33.(1);(2)x(x+3)(x﹣3);(3)xy( x﹣5)2.
34.(1);(2)41;(3)
35.(1)3
(2)①9;②20
36.(1)
(2)
37.(1)
(2)或
38.(1)
(2)
39.(1)(a+b)2=a2+2ab+b2
(2)①12;②8
40.(1)
(2)
(3)
41.(1);
(2)34平方厘米.
42.
43.(1)
(2)
(3)
44.(1)或或
(2)当时,代数式的值最小
(3)当该长方形的相邻两边长均为米时,围成的长方形面积最大,最大面积是平方米
45.(1)是
(2)③
(3)①:④;②:或或或
46.(1)
(2)
47.(1)
(2)
48..
49.(1)
(2)
50.(1)120
(2)3或12或15
期中真题专项复习05解答题
一、解答题
1.(2024七下·淮安期中)【观察】如图①是一个长为、宽为b的长方形,沿图中虚线用剪刀平均分成四块小长方形,然后用四块小长方形拼成一个大正方形,如图②所示,请直接写出,,之间的等量关系____________________________;
【应用】若,,则_______________;
【拓展】如图③,正方形的边长为x,,,长方形的面积是200,四边形和四边形都是正方形,四边形是长方形,求图中阴影部分的面积.
2.(2024七下·盐城期中)教科书中这样写道:“我们把多项式及叫做完全平方式”,如果一个多项式不是完全平方式,我们常做如下变形:先添加一个适当的项,使式子中出现完全平方式,再减去这个项,使整个式子的值不变,这种方法叫做配方法.配方法是一种重要的解决问题的数学方法,不仅可以将一个看似不能分解的多项式分解因式,还能解决一些与非负数有关的问题或求代数式最大值,最小值等.
例如:分解因式
;
例如:求代数式的最小值为.可知当时,有最小值,最小值是,根据阅读材料用配方法解决下列问题:
(1)分解因式:______;
(2)当a为何值时,多项式有最大值,并求出这个最大值;
(3)当a,b为何值时,多项式有最小值,并求出这个最小值.
3.(2024七下·徐州期中)如图,已知,求的度数.
4.(2024七下·南京期中)(1)已知,求的值;
(2)已知,,求:
①的值;
②的值.
5.(2024七下·淮安期中)规定:各边相等,各角也相等的多边形叫正多边形.
一个机器人以的速度在平地上按如下要求行走,
(1)该机器人从开始到停止所走过的路程形成的图形是_____;
(2)该机器人从开始到停止所需时间为_______;
(3)若机器人还差就第次回到点处,则它所走过的路程为_____.
6.(2024七下·淮安期中)完全平方公式经常可以用作适当变形来解决很多的数学问题.
(1)若,,求的值;
(2)请直接写出下列问题答案:
①若,,则______;
②若,则______.
(3)如图,边长为6的正方形中放置两个长和宽分别为,的长方形,若长方形的周长为16,面积为15.75,求图中阴影部分面积.
7.(2024七下·淮安期中)已知,,
求①的值;②的值.
8.(2024七下·新沂期中)如图,在中.
(1)如图1,若,与的平分线交于点.求的度数;
(2)如图2,若,的外角与的平分线交于点.求的度数(用来表示);
(3)如图3,的等分线()与外角的等分线()交于点,若,,则 .
9.(2024七下·新沂期中)如图,在中,点、分别在、上,且,,,求的度数.
10.(2024七下·苏州工业园期中)将完全平方公式作适当变形,可以用来解决很多数学问题.
(1)观察图1,写出代数式,,之间的等量关系:______;
(2)若,,则 _____;
(3)如图2,边长为5的正方形中放置两个长和宽分别为,(,)的长方形,若长方形的周长为12,面积为,求图中阴影部分的面积的值.
11.(2024七下·泰州期中)我们在分析解决某些数学问题时,经常要比较两个数或代数式的大小.而解决问题的策略一般要进行一定的转化,其中“作差法”就是常用的方法之一,所谓“作差法”:就是通过作差、变形,并利用差的符号来确定它们的大小,即要比较代数式M、N的大小,只要作出它们的差,若,则;若,则.若,则,
请你用“作差法”解决以下问题:
(1)如图,试比较图①、图②两个矩形的周长的大小.
(2)如图③,把边长为的大正方形分割成两个边长分别是a、b的小正方形及两个矩形,试比较两个小正方形的面积之和与两个矩形面积之和的大小.
12.(2024七下·江阴期中)对于平面内的∠M和∠N,若存在一个常数k>0,使得∠M+k∠N=360°,则称∠N为∠M的k系补周角.如若∠M=90°,∠N=45°,则∠N为∠M的6系补周角.
(1)若∠H=120°,则∠H的4系补周角的度数为 °;
(2)在平面内AB∥CD,点E是平面内一点,连接BE,DE;
①如图1,∠D=60°,若∠B是∠E的3系补周角,求∠B的度数;
②如图2,∠ABE和∠CDE均为钝角,点F在点E的右侧,且满足∠ABF=n∠ABE,∠CDF=n∠CDE(其中n为常数且n>1),点P是∠ABE角平分线BG上的一个动点,在P点运动过程中,请你确定一个点P的位置,使得∠BPD是∠F的k系补周角,并直接写出此时的k值(用含n的式子表示).
13.(2024七下·江阴期中)如图,是的高,是的角平分线,F是中点,.
(1)求的度数;
(2)若与的周长差为3,,则 .
14.(2024七下·扬州期中)(1)若,求的值.
(2)已知,,求的值.
15.(2024七下·宿城期中)如图,是一个正方体的展开图,标注字母“a”的面是正方体的正面,如果正方体相对两个面上的代数式的值相等,试求代数式(2x﹣y)(2x+y)﹣(2x﹣y)2的值.
16.(2024七下·秦安期中)某铁件加工厂用如图1的长方形和正方形铁片(长方形的宽与正方形的边长相等)加工成如图2的竖式与横式两种无盖的长方体铁容器.(加工时接缝材料不计)
(1)如果加工竖式铁容器与横式铁容器各1个,则共需要长方形铁片 张,正方形铁片 张.
(2)现有长方形铁片2014张,正方形铁片1176张,如果加工成这两种铁容器,刚好铁片全部用完,那么加工的竖式铁容器、横式铁容器各有多少个
(3)把长方体铁容器加盖可以加工成为铁盒.现用35张铁板做成与如图相同的长方形铁片和正方形铁片,已知每张铁板可做成3个长方形铁片或4个正方形铁片,也可以将一张铁板做成1个长方形铁片和2个正方形铁片.该如何充分利用这些铁板加工成铁盒,最多可以加工成多少个铁盒
17.(2024七下·泰州期中)解二元一次方程组:
18.(2024七下·宝安期中)如图1,有A型,B型正方形卡片和C型长方形卡片各若干张.
(1)用1张A型卡片,2张B型卡片,3张C型卡片拼成一个长方形,如图2,用两种方法计算这个长方形面积,可以得到一个等式:__________________________;
(2)选取1张B型卡片,6张C型卡片,__________张A型卡片,可以拼成一个正方形,这个正方形的边长用含a,b的式子表示为__________;
(3)如图3,在长方形中,分别为上一点,且,在左侧放置1张A型卡片,在下方放置一张B型卡片.若图中的长方形的面积为8,求一张A型卡片和一张B型卡片面积之和.
19.(2024七下·鼓楼期中)如图①所示,在中,若,则称,分别为的“三分线”.其中,是“邻三分线”,是“邻三分线”.
(1)如图②,在中,,,若的邻三分线交于点,则________;
(2)如图③,在中,是的邻三分线,是的邻三分线,若,求的度数;
(3)在中,是的外角,的三分线与的邻三分线交于点.若,,直接写出的度数.(用含、的代数式表示)
20.(2023七下·中江期中)如图①,在平面直角坐标系中,,,且满足,过作轴于.
(1)求三角形的面积;
(2)如图②,若过作交轴于,且,分别平分,,求的度数;
(3)在轴上是否存在点,使得三角形和三角形的面积相等?若存在,求出点的坐标;若不存在,请说明理由.
21.(2024七下·如东期中)在等式中,当时,;当时,;当与时,的值相等.求,,的值.
22.(2024七下·盐城期中)如图,用4个长是a,宽是b的长方形拼成了一个如图2所示的“回形”正方形.
(1)拼图前后,请写出所用图形(4个长方形)的面积的计算方法:拼图前: ;拼图后: ;因为拼图前后的面积不变,所以可得恒等式: ;
(2)利用(1)中得到的恒等式,解决下面的问题:已知,,求的值.
23.(2024七下·盐城期中)如图,是的高,,,求的度数.
24.(2024七下·昆山期中)根据下列条件回答问题
(1)已知,求n的值;
(2)已知,,求的值.
25.(2024七下·昆山期中)如图,在中,平分交于点,是的高,与交于点.若,,求的度数.
26.(2024七下·淮阴期中)【结论发现】
小明在完成教材第43页第21题后发现:三角形的一个内角平分线与另一内角的外角平分线的夹角的度数是三角形第三内角度数的一半.
【结论应用】
(1)如图1,在中,,点E是的内角平分线与外角平分线的交点,则的度数为 °;
(2)如图2,在中,,延长至点E,延长至点D,已知、的角平分线与的角平分线及其反向延长线交于P、F,求的度数;
【拓展延伸】
(3)如图3,四边形的内角与外角的平分线形成如图所示形状.
①已知,,求的度数;
②直接写出与的数量关系.
27.(2024七下·苏州工业园期中)如图,在中,,是线段延长线上的动点,在线段上取一点,使.
(1)当点在线段上时,且,求的度数;
(2)若,且是直角三角形,则______
28.(2024七下·苏州工业园期中)已知:,,求下列各式的值:
(1);
(2);
(3).
29.(2024七下·南京期中)如图,已知长方形中,,,点是的中点,点从点出发在上以每秒的速度向点运动,运动时间设为1秒.(假定)
(1)当秒时,求阴影部分(即三角形)的面积;
(2)用含的式子表示阴影部分的面积;
(3)过点作交于点,过点作交于点,请直接写出在点运动过程中,和的数量关系.
30.(2024七下·海安期中)已知关于 x,y 的二元一次方程组 的解满足.
(1)求 k 的取值范围;
(2)在 (1) 的条件下,若不等式的解为,请写出符合条件的 k 的整数值.
31.(2024七下·江阴期中)已知,平分,点,,分别是射线,,上的动点,,不与点重合),连接,连接交射线于点,设.
(1)如图1,若,
①的度数是 ;
②当时,的度数是 ;当时,的度数是 ;
(2)在一个四边形中,若存在一个内角是它的对角的2倍,我们称这样的四边形为“完美四边形”,如图2,若,延长交射线于点,当四边形为“完美四边形”时,求的值.
32.(2024七下·江阴期中)2002年8月,在北京召开的国际数学家大会会标取材于我国古代数学家赵爽发现的“弦图”,它是由四个大小相等,形状相同的直角三角形与中间的小正方形拼 成的一个大正方形(如图1),设直角三角形的较短直角边为a,较长直角边为b,最长的斜边为c.
(1)若,则图1中大正方形的面积为 ;
(2)猜想之间的数量关系,并按给出的格式说明理由.
∵ , = ,
∴ ;
(3)若图1中大正方形的面积是15,小正方形的面积是1,现将四个直角三角形按如图 2的形式重新摆放,那么图2中最大的正方形的面积为 .
33.(2024七下·江阴期中)因式分解:
(1) (2) x3﹣9x; (3)x3y﹣10x2y+25xy
34.(2024七下·锡山期中)[知识生成]
(1)通常,用两种不同的方法计算同一个图形的面积,可以得到一个恒等式.
如图1,有四张长为、宽为的长方形纸片按如图方式拼成了一个正方形,请你通过拼图写出、、之间的等量关系是______.
[知识应用]
(2)若,,求的值;
[知识迁移]
(3)如图2,为创办文明校园,美化校园环境,某校计划要在面积为的长方形空地中划出长方形和长方形,两个长方形重合部分刚好建一个长为,宽为的喷泉水池,现将图中阴影部分区域作为花圃,且花圃总周长为,则的长度为多少米?
35.(2024七下·邳州期中)阅读材料:已知,,求的值.
解:.
参考上面的方法求解下列问题:
(1)已知满足,求的值;
(2)如图①,已知长方形的周长为14,分别以为边,向外作正方形,且正方形的面积和为31.
①求长方形的面积;
②如图②,连接,求的面积.
36.(2024七下·邳州期中)如图,是的中线,是的高,,,,.
(1)求高的长;
(2)求的面积.
37.(2024七下·无锡期中)如图,在中,,,D是边上一点,将沿过点D的直线折叠,使点B落在下方的点F处,折痕交于点E.
(1)当时,求的度数;
(2)当的一边与平行时,求的度数.
38.(2024七下·无锡期中)如图,在中,点D、G分别在边、上,点E、F在边上,且,,.
(1)求的度数;
(2)若,求的度数.
39.(2024七下·南京期中)在课后服务课上,老师准备了若干个如图1的三种纸片,A种纸片是边长为a的正方形,B种纸片是边长为b的正方形,C种纸片是长为b,宽为a的长方形,并用A种纸片一张,B种纸片一张,C种纸片两张拼成如图2的大正方形.
(1)根据图2,写出一个我们熟悉的数学公式 .
(2)根据(1)中的数学公式,解决如下问题:
①已知:a+b=7,a2+b2=25,求ab的值.
②如果一个长方形的长和宽分别为(8﹣x)和(x﹣2),且(8﹣x)2+(x﹣2)2=20,求这个长方形的面积.
40.(2024七下·苏州期中)小明在学习配方法时,将关于x的多项式配方成,发现当取任意一对互为相反数的数时,多项式的值是相等的.例如:当时,即或-1时,的值均为6;当时,即或-2时,的值均为11.于是小明给出一个定义:对于关于x的多项式,若当取任意一对互为相反数的数时,该多项式的值相等,就称该多项式关于对偶,例如关于对偶.
请你结合小明的思考过程,运用此定义解决下列问题:
(1)多项式关于__________对偶;
(2)当或时,关于x的多项的值相等,求b的值;
(3)若整式)关于对偶,求n的值.
41.(2024七下·苏州期中)如图,将一张大长方形纸板按图中虚线裁剪成9块,其中有2块是边长为a厘米的大正方形,2块是边长都为b厘米的小正方形,5块是长为a厘米,宽为b厘米的相同的小长方形,且.
(1)观察图形,可以发现代数式可以因式分解为______.
(2)若图中空白部分的面积为20平方厘米,大长方形纸板的周长为30厘米,求图中阴影部分的面积.
42.(2024七下·苏州期中)如图,已知,且,求的度数.
43.(2024七下·鼓楼期中)已知,在中,,,,是射线,上的点,连接.分别过,作,外角的角平分线相交于点.
(1)如图1,点,在线段,延长线上,若,求.
(2)如图2,点在线段延长线上,点在线段上,与相交于点.若,求.
(3)如图3,点在线段上运动(不与,重合),点在线段的延长线上运动,请直接写出的取值范围.
44.(2024七下·泗洪期中)根据完全平方公式,把形如的二次三项式(或其一部分)配成完全平方式的方法叫做“配方法”.例如把配方如下:.请完成下列问题:
(1)填空:配方多项式的结果为 ;
(2)当等于多少时,代数式的值最小?
(3)用一根长为米的绳子围成一个长方形,请问长方形的边长为多少时,围成的长方形面积最大?最大面积是多少?
45.(2024七下·南京期中)如果三角形中任意两个内角与满足,那么我们称这样的三角形为“准直角三角形”
(1)在中,若,,则______“准直角三角形”(填写是或不是);
(2)如果是“准直角三角形”,那么是______,(从下列四个选项中选择,填写符合条件的序号)(①锐角三角形;②直角三角形;③钝角三角形;④都有可能),请说明理由;
(3)如图,在中,,,平分交于点.
①若交于点,在①,②,③,④中“准直角三角形”是______(填写序号);
②在直线上取一点,当是“准直角三角形”时,直接写出的度数.
46.(2024七下·扬州期中)已知,当时,y的值为2,当时,y的值为14.
(1)求p,q的值;
(2)求时,y的值.
47.(2024七下·南京期中)分解因式:
(1);
(2).
48.(2024七下·南京期中)如图,在中,是的高,平分,若.求的度数.
49.(2024七下·盐城期中)因式分解:
(1);
(2).
50.(2024七下·钟楼期中)如图,将两个完全相同的直角三角板、放置在一起,点B、D重合,点F在上,与交于点G.已知,.
(1)_____________________°;
(2)现将图中的绕点F按每秒的速度沿逆时针方向旋转一定角度,旋转时间为t秒,在旋转的过程中,当恰有一边与平行时,请直接写出t的值.
答案解析部分
1.观察:;应用:;拓展:900
2.(1);
(2)2,22;
(3),,20.
3.
4.(1);(2)①;②
5.(1)正九边形;
(2)18;
(3).
6.(1)3
(2)①② 17
(3)12.5
7.①6;②
8.(1)
(2)
(3)4
9.
10.(1)
(2)28,20
(3)
11.(1)
(2)
12.(1)60
(2)①∠B=75°,②当BG上的动点P为∠CDE的角平分线与BG的交点时,满足∠BPD是∠F的k系补周角,此时k=2n.
13.(1)
(2)10
14.(1)16;(2)
15.-40
16.(1)共需要长方形铁片7张,正方形铁片3张;(2)加工的竖式容器有100个,横式容器有539个;(3)最多可做19个.
17.
18.(1)
(2)9,
(3)一张A型卡片和一张B型卡片面积之和为20
19.(1)
(2)
(3)当是“邻三分线”时,;当是“邻三分线”时,
20.(1)4
(2)
(3)存在,点的坐标为或
21.
22.(1);;
(2)
23.
24.(1)
(2)25
25.
26.(1)20;(2);(3)①;②
27.(1)
(2)或
28.(1)100
(2)4
(3)
29.(1)22.5
(2)
(3)
30.(1)
(2) ,
31.(1)①;②,
(2)的值是或或
32.(1)100
(2),;;
(3)29
33.(1);(2)x(x+3)(x﹣3);(3)xy( x﹣5)2.
34.(1);(2)41;(3)
35.(1)3
(2)①9;②20
36.(1)
(2)
37.(1)
(2)或
38.(1)
(2)
39.(1)(a+b)2=a2+2ab+b2
(2)①12;②8
40.(1)
(2)
(3)
41.(1);
(2)34平方厘米.
42.
43.(1)
(2)
(3)
44.(1)或或
(2)当时,代数式的值最小
(3)当该长方形的相邻两边长均为米时,围成的长方形面积最大,最大面积是平方米
45.(1)是
(2)③
(3)①:④;②:或或或
46.(1)
(2)
47.(1)
(2)
48..
49.(1)
(2)
50.(1)120
(2)3或12或15
同课章节目录
