期中真题专项复习04 解答题(含答案)--2024-2025学年八年级数学下册(苏科版)
文档属性
| 名称 | 期中真题专项复习04 解答题(含答案)--2024-2025学年八年级数学下册(苏科版) |  | |
| 格式 | docx | ||
| 文件大小 | 768.4KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-03-30 06:08:04 | ||
图片预览



文档简介
2024-2025学年八年级数学下册(苏科版)
期中真题专项复习04 解答题
一、解答题
1.(2024八下·江苏期中)在平面直角坐标系中,矩形OACB的顶点O在坐标原点,顶点A、B分别在x轴、y轴的正半轴上,OA=3,OB=4,D为OB的中点,点E为边OA上的一个动点.
(1)求线段CD所在直线的解析式;
(2)当△CDE的周长最小时,求此时点E的坐标;
(3)当点E为OA中点时,坐标平面内,是否存在点F,使以D、E、C、F为顶点的四边形是平行四边形?若存在,请直接写出F点的坐标;若不存在,请说明理由.
2.(2024八下·泰兴期中)某中学组织学生到离学校15km的东山游玩,先遣队与大队同时出发,先遣队的速度是大队的速度的1.2倍,结果先遣队比大队早到0.5h,先遣队的速度是多少?大队的速度是多少?
3.(2024八下·苏州工业园期中)如图所示,点是反比例函数图象上的一点,轴于点,点是反比例函数图象上的一个动点,且.
(1)直接写出不等式中的范围______.
(2)求点的坐标.
4.(2024八下·盐城期中)在一个不透明的袋子中装有9个红球和6个黄球,这些球除颜色外都相同,将袋子中的球充分摇匀后,随机摸出一球.
(1)分别求出摸出的球是红球和黄球的概率.
(2)为了使摸出两种球的概率相同,再放进去7个同样的红球或黄球,那么这7个球中红球和黄球的数量分别应是多少?
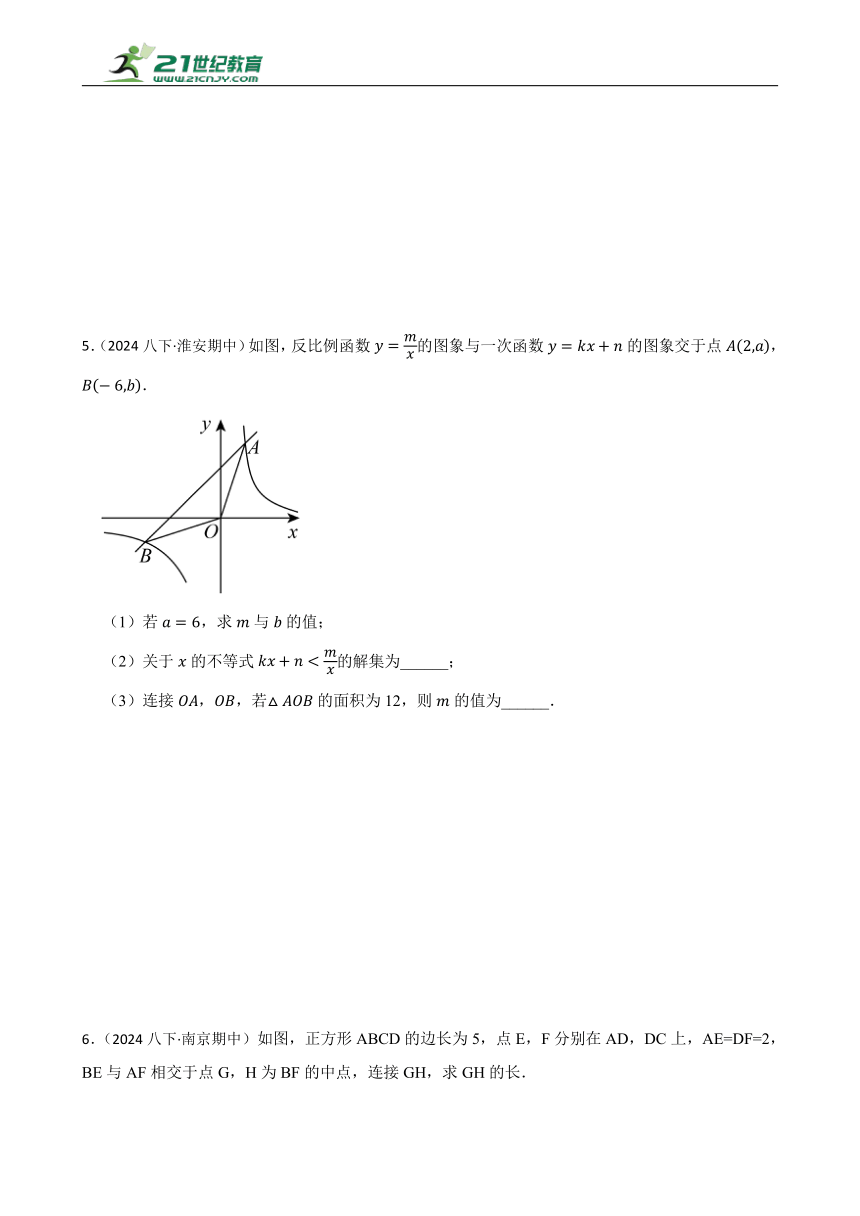
5.(2024八下·淮安期中)如图,反比例函数的图象与一次函数的图象交于点,.
(1)若,求与的值;
(2)关于的不等式的解集为______;
(3)连接,,若的面积为12,则的值为______.
6.(2024八下·南京期中)如图,正方形ABCD的边长为5,点E,F分别在AD,DC上,AE=DF=2,BE与AF相交于点G,H为BF的中点,连接GH,求GH的长.
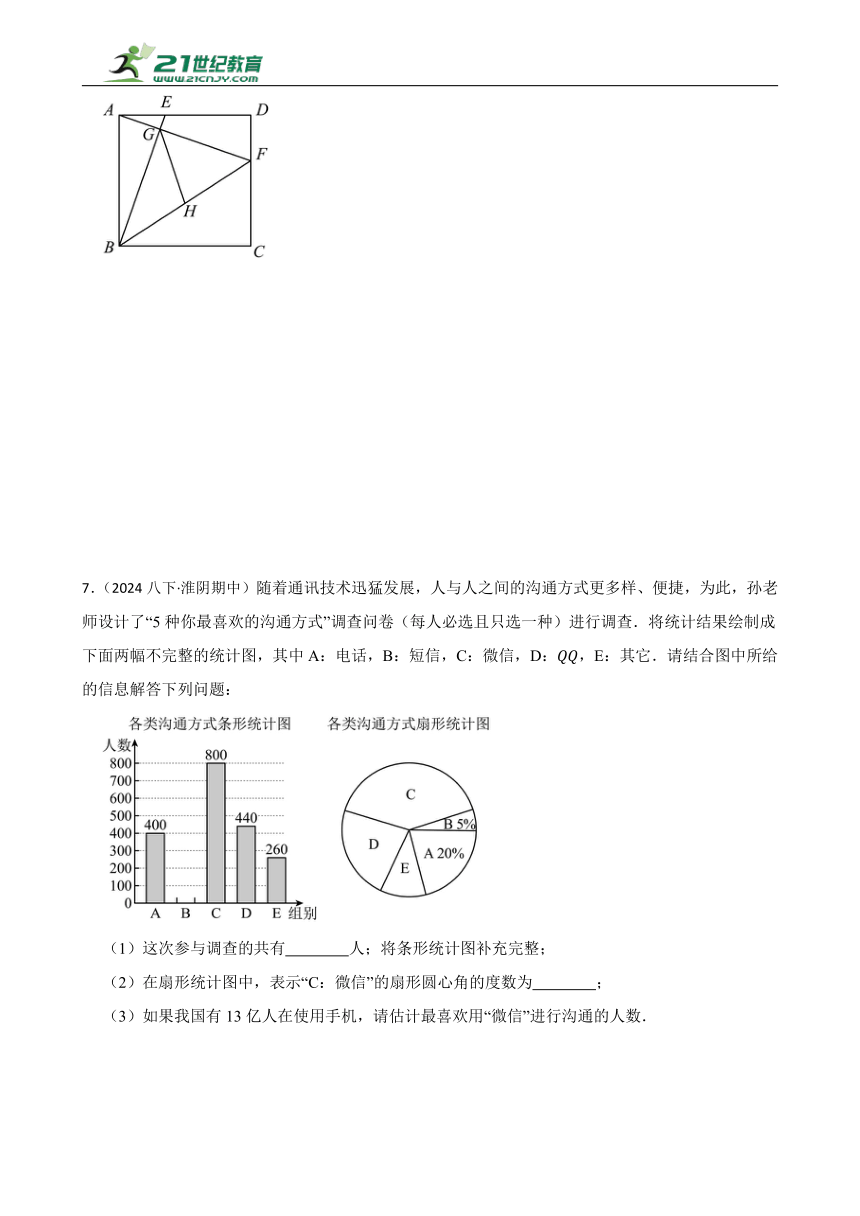
7.(2024八下·淮阴期中)随着通讯技术迅猛发展,人与人之间的沟通方式更多样、便捷,为此,孙老师设计了“5种你最喜欢的沟通方式”调查问卷(每人必选且只选一种)进行调查.将统计结果绘制成下面两幅不完整的统计图,其中A:电话,B:短信,C:微信,D:,E:其它.请结合图中所给的信息解答下列问题:
(1)这次参与调查的共有 人;将条形统计图补充完整;
(2)在扇形统计图中,表示“C:微信”的扇形圆心角的度数为 ;
(3)如果我国有13亿人在使用手机,请估计最喜欢用“微信”进行沟通的人数.
8.(2024八下·南通期中)如图,在平面直角坐标系中,四边形是平行四边形,为坐标原点,点A的坐标是,线段交轴于点,点的坐标是,线段,动点从点出发,沿射线的方向以每秒2个单位的速度运动,同时动点从点出发,以每秒1个单位的速度向终点运动,当点运动到点时,点随之停止运动,运动时间为秒.
(1)用t的代数式表示:_______,_______;
(2)若以为顶点的四边形是平行四边形时,求的值;
(3)若为等腰三角形,直接写出的值.
9.(2024八下·南通期中)某小区有一块长方形绿地,长为米,宽为米,现在要在长方形绿地中修建两个形状大小相同的小长方形花坛(即图中阴影部分),每个小长方形花坛的长为米,宽为米.
(1)求长方形绿地的周长;
(2)除花坛外,其他地方全修建成通道,通道需铺上造价为55元/平方米的地砖,则购买地砖需要多少钱?
10.(2024八下·丹徒期中)在一个不透明的袋子中装有仅颜色不同的12个小球,其中红球4个,黑球8个.
(1)进行如下的实验操作:先从袋子中取出个红球后,再从袋子中剩余的球中随机摸出1个球,此时将“第二次摸出的1个球是黑球”记为事件A.
①若事件A是必然事件,则m的值是______;
②若事件A是随机事件,则m的值是_____;
(2)从袋子中取出n个红球,再从袋子中剩余的球中随机摸出1个球,若第二次摸到的1个球是黑球的可能性大小是,求n的值.
11.(2024八下·姑苏期中)如图,直线:与轴、轴分别交于点,与直线:交与点.
(1)点的坐标为______(用含的代数式表示);
(2)点在轴上,横坐标为,点为直线上一点,当以为顶点的四边形为平行四边形时,且面积为时,求点的坐标;
(3)作点关于直线的对称点,当点落在直线上时,求点到直线的距离.
12.(2024八下·姑苏期中)如图,正方形,边长为,动点从点以每秒的速度沿向运动,动点从点以每秒的速度沿向运动,连结.两点同时出发,设运动时间为秒.
(1)求运动时间为何值时的面积为;
(2)连结、,是否存在某一时刻,使为等腰三角形,若存在,求出所有的值;若不存在,请说明理由.
13.(2024八下·姑苏期中)不透明的袋中有若干个红球和黑球,每个球除颜色外无其他差别.现从袋中随机摸出1个球,记下颜色后放回并搅匀,经过大量重复试验发现摸到黑球的频率逐渐稳定在附近.
(1)估计摸到黑球的概率是________;
(2)如果袋中的黑球有8个,求袋中共有几个球;
(3)在(2)的条件下,又放入个黑球,再经过大量重复试验发现摸到黑球的频率逐渐稳定在附近,直接写出的值.
14.(2024八下·江阴期中)如图,在直角坐标系中,,,一次函数的图象与x轴交于A点.
(1)A点坐标为 ;
(2)一次函数图象上是否存在一点C,使得四边形是平行四边形?如存在,求出C点坐标.若不存在,说明理由;
(3)将绕点O顺时针旋转,旋转得,问:能否使以点O、、D、为顶点的四边形是平行四边形?若能,求点的坐标;若不能,请说明理由.
15.(2024八下·无锡期中)在如图所示的平面直角坐标系中,正方形边长为2,点C的坐标为.
(1)如图1,动点D在边上,将沿直线折叠,点B落在点处,连接并延长,交于点E.
①当时,点D的坐标是______;
②若点E是线段的中点,求此时点D与点的坐标;
(2)如图2,动点D,G分别在边上,将四边形沿直线折叠,使点B的对应点始终落在边上(点不与点O,A重合),点C落在点处,交于点E.设,四边形的面积为S,直接写出S与t的关系式.
16.(2024八下·宜兴期中)我校在开学前去商场购进A,B两种品牌的乒乓球拍,购买A品牌球拍共花费1800元,购买B品牌球拍共花费700元,且购买A品牌球拍数量是购买B品牌球拍的3倍,已知购买一副B品牌球拍比购买一副A品牌球拍多花5元.
(1)求购买一副A品牌、一副B品牌球拍各需多少元?
(2)为了进一步发展“校园乒乓球”,学校在开学后再次购进了A,B两种品牌的球拍,每种品牌的球拍都不少于16副,在购买时,商场对两种品牌的球拍的销售单价进行了调整,A品牌球拍销售单价比第一次购买时提高了5%,B品牌球拍按第一次购买时销售单价的6折出售且总花费恰好为903元,那么此次有哪些购买方案?
17.(2024八下·广陵期中)在平面直角坐标系中,定义:横坐标与纵坐标均为整数的点为整点.如图,已知双曲线经过点,在第一象限内存在一点,满足.
(1)求的值
(2)如图1,过点分别作平行于轴,轴的直线,交双曲线于点,记为线段、双曲线所围成的区域为(含边界),
①当时,区域的整点个数为 ;
②当区域的整点个数为4时,点横坐标满足,则纵坐标取值范围为 ;
(3)直线将分成两部分,直线上方(不包含直线)区域记为,直线下方(不包含直线)区域记为,当的整点个数之差不超过2时,则的取值范围为 .
18.(2024八下·南京期中)某商场设立了一个可以自由转动的转盘,并做如下规定:顾客购物80元以上就获得一次转动转盘的机会,当转盘停止时,指针落在哪一区域就可以获得相应的奖品,下表是活动进行中的一组统计数据.
转动转盘的次数 100 150 200 500 800 1000
落在“洗衣粉”区域的次数 68 111 136 345 564 701
落在“洗衣粉”区域的频率 0.68 a 0.68 0.69 b 0.70
(1) , ;
(2)转动该转盘一次,获得洗衣粉的概率的估计值是多少
19.(2024八下·鼓楼期中)如图,平面直角坐标系xOy中,点O为坐标原点,四边形OABC为矩形,A(10,0),C(0,4),点D是OA的中点,点P在边BC上以每秒1个单位长的速度由点C向点B运动.
(1)当t= 时,四边形PODB是平行四边形;
(2)在线段PB上是否存在一点Q,使得四边形ODQP为菱形?若存在,求出当四边形ODQP为菱形时t的值,并求出Q点的坐标;若不存在,请说明理由;
(3)当△OPD为等腰三角形时,写出点P的坐标 (直接写出答案).
20.(2024八下·江阴期中)如图,在平面直角坐标系中,直线交轴于点,交轴于点,直线经过点且交轴正半轴于点,已知.
(1)点的坐标是 ,直线的表达式是 .
(2)若点为线段上一点,且满足,点为直线上一动点,在轴上是否存在点,使以点为顶点的四边形为平行四边形?如存在,请直接写出点的坐标;若不存在,说明理由.
(3)点为线段中点,点为轴上一动点,以为直角边作等腰直角,当点落在直线上时,求点的坐标.
21.(2024八下·淮安期中)如图,在矩形ABCD中,AC、BD相交于点O,DE⊥AC于点E.若,求∠CDE的度数.
22.(2024八下·苏州期中)已知矩形中,,的垂直平分线分别交于点E、F,垂足为O.
(1)如图1,连接,直接写出的长 ;
(2)如图2,动点P、Q分别从A、C两点同时出发,沿 和各边匀速运动一周.即点P自A→F→B→A停止,点Q自C→D→E→C停止.在运动过程中:
①已知点P的速度为每秒,点Q的速度为每秒,运动时间为t秒,当以A、P、C、Q四点为顶点的四边形是平行四边形时,求t的值;
②若点P、Q的运动路程分别为a、b(单位:cm,),以A、C、P、Q四点为顶点的四边形是平行四边形,求a与b满足的数量关系式.
23.(2024八下·苏州期中)如图,在中,,平分交于点D,点F在上,连接,E为的中点,交于点G,连接.
(1)若,求的长;
(2)若点F在直线上,当时,求的长.
24.(2024八下·苏州期中)如图,已知, 是一次函数图像与反比例函数图像的两个交点.
(1)求反比例函数和一次函数的解析式;
(2)求直线与轴的交点的坐标及的面积;
(3)请结合图像直接写出不等式的解集为 .
25.(2024八下·苏州期中)已知是的反比例函数,且当时,.
(1)直接写出函数与之间的关系式为 ;
(2)借助函数图象,求当时,的取值范围.
26.(2024八下·苏州期中)已知反比例函数的图象经过点.
(1)求反比例函数表达式;
(2)若点在该函数图象上,求m的值.
27.(2024八下·苏州工业园期中)在正方形中,是的中点,点从点出发沿的路线匀速运动,移动到点时停止.
(1)如图1,若正方形的边长为12,点的运动速度为2单位长度/秒,设秒时,正方形与重叠部分的面积为.
①当时,______;当时,______.
②求为何值时,以点为顶点的四边形是平行四边形?
(2)如图2,若点从出发沿的路线匀速运动.两点同时出发,点的速度大于点的速度,当到终点时,也停止运动.设秒时,正方形与(包括边缘及内部)重叠部分的面积为,与的函数图象如图3所示.
①,两点在第______秒相遇;正方形的边长是______.
②点的速度为______单位长度/秒;点的速度为______单位长度/秒.
③当为何值时,重叠部分面积等于32?
28.(2024八下·淮阴期中)如图,矩形的对角线、相交于点O,,cm.
(1)求的度数;
(2)求矩形对角线的长.
29.(2024八下·涟水期中)在矩形中,相交于点,平分,交于点.若,求的度数.
30.(2024九上·温州期中)在一只不透明的口袋里,装有若干个除了颜色外均相同的小球,某数学学习小组做摸球试验,将球搅匀后从中随机摸出一个球记下颜色,再把它放回袋中,不断重复.如下表是活动进行中的一组统计数据:
摸球的次数
摸到白球的次数
摸到白球的频率
(1)上表中的________,________;
(2)“摸到白球的”的概率的估计值是________(精确到);
(3)如果袋中有个白球,那么袋中除了白球外,还有________个其它颜色的球.
31.(2024八下·昆山期中)如图,在四边形ABCD中,,,,,.动点M从点B出发沿边以速度向终点C运动;同时动点N从点D出发,以速度沿射线运动,当点M到达终点时,点N也随之停止运动,设点M运动的时间为.
(1)当时,__________;
(2)是否存在t的值,使得A,B,M,N为顶点的四边形为平行四边形?若存在,求出t的值;若不存在,请说明理由;
(3)若动点M关于直线对称的点恰好落在直线上,请直接写出t的值.
32.(2024八下·昆山期中)定义:若点A在一个函数图象上,且点A的横、纵坐标相等,则称点A为这个函数的“等点”.
(1)关于“等点”,下列说法正确的有__________;
①函数有两个“等点”;②函数有一个“等点”;③函数没有“等点”.
(2)已知反比例函数与一次函数的图象上有同一个“等点”,求反比例函数的表达式;
(3)函数的图象上有两个“等点”A、B,设A、B两点之间的距离为m,若,则k的取值范围是__________.
33.(2024八下·昆山期中)如图,点A是反比例函数图象上一点,过点A作y轴的平行线,交函数的图象于点B,连接,交反比例函数的图象于点C,已知.
(1)求k的值;
(2)连接,若点A的横坐标为4,求的面积.
34.(2024八下·昆山期中)解分式方程:
35.(2024八下·扬州期中)已知关于的分式方程
(1)若该方程的增根为,求的值;
(2)若该方程有增根,求的值.
(3)若该方程无解,求的值.
36.(2024八下·盐都期中)如图,在矩形ABCD中,AB=4,BC=5,延长BC到点E,使CE=3,连接DE.动点P从点B出发,以每秒2个单位的速度沿折线BC-CD向终点D运动,设点P运动的时间为t秒.(t>0)
(1)DE=______;
(2)连接AP,当四边形APED是菱形时,求菱形APED的周长;
(3)连接BP、PD,设四边形ABPD的面积为S,求S与t之间的函数关系式;
(4)直接写出点P到四边形ABED相邻两边距离相等时t的值.
37.(2024八下·盐都期中)如图,已知四边形是正方形,、分别是和的延长线上的点,且,连接、、,
(1)填空:可以由绕旋转中心______点,按顺时针方向旋转______度得到;
(2)若,求四边形的面积.
38.(2024八下·吴江期中)如图,正比例函数与反比例函数的图像交于点,点是反比例函数图像上的点,连接.
(1)求,和的值;
(2)若点是正比例函数图像上的点,且的面积是4,求点的坐标.
39.(2024八下·镇江期中)在一个不透明的盒子中装有颜色不同的8个小球,其中红球3个,黑球5个.
(1)先从袋中取出m(m>1)个红球,再从袋中随机摸出1个球,将“摸出黑球”记为事件A.请完成下列表格:
事件A 必然事件 随机事件
m的值
(2)先从袋中取出m个红球,再放入m个一样的黑球并摇匀,随机摸出1个球是黑球的概率是,求m的值.
40.(2024八下·淮安期中)如图1,反比例函数与一次函数的图象交于点,点,一次函数与轴相交于点.
(1)求反比例函数和一次函数的表达式;
(2)连接,,求的面积;
(3)当时,x的范围为 .
41.(2024八下·扬州期中)如图,以矩形OABC的顶点O为坐标原点,边OA所在直线为x轴,OC所在直线为y轴,建立如图所示的直角坐标系,已知A(a,0),C(0,b),其中a,b满足|a-4|+(b-6)2=0,点P从点O出发沿OA以1cm/s的速度向点A移动,同时点Q从点B出发沿BA方向以1cm/s的速度向点A移动,设运动时间为t秒(0≤t≤4).
(1)求出a,b的值.
(2)当t=2时,判断△PCQ的形状,并说明理由.
42.(2024八下·扬州期中)如图,在中,的平分线交于点E,若,求、的度数.
答案解析部分
1.(1)直线 CD:;(2);(3)存在,或或
2.先遣队的速度是6km/h,大队的速度是5km/h
3.(1)或者
(2)点P的坐标是或
4.(1),;(2)2个和5个
5.(1),
(2)或
(3)9
6.
7.(1)2000;如图所示
(2)
(3)5.2亿人
8.(1);
(2)6或
(3)4或6或
9.(1)米
(2)3080元
10.(1)4;2或3
(2)2
11.(1);
(2)点的坐标为或;
(3).
12.(1)运动时间时的面积为
(2)或或或时,为等腰三角形
13.(1)
(2)
(3)
14.(1);
(2)存在,
(3)的坐标为或或.
15.(1)①;点D的坐标为,点的坐标为
(2)
16.(1)一副A品牌球拍需30元、一副B品牌球拍需35元
(2)有两个方案,方案一:购买18副A品牌球拍与16副B品牌球拍
方案二:购买16副A品牌球拍与19副B品牌球拍
17.(1)4
(2)①11;②
(3)
18.(1)0.74;0.705
(2)0.70
19.(1)t=5;(2)存在,t=3,点Q的坐标为(8,4);(3)P1(2,4),P2(2.5,4),P3(3,4),P4(8,4)
20.(1),;
(2)存在,点坐标为或;
(3)点坐标为或.
21.
22.(1)
(2)①;②
23.(1)
(2)
24.(1)反比例函数的解析式为,一次函数的解析式为
(2),的面积为
(3)或
25.(1)
(2)
26.(1);
(2)或.
27.(1)①114;60;②9秒
(2)①4秒;8;②4;2;③或6,
28.(1)
(2)2
29.
30.(1),
(2)
(3)除白球外,还有大约个其它颜色的小球
31.(1)
(2)或
(3)或
32.(1)①③
(2)
(3)
33.(1)
(2)
34.无解
35.(1)
(2)或
(3)或或
36.(1)5;
(2)20;
(3)S=;
(4)t=2或或.
37.(1)A,90
(2)64
38.(1),,
(2),
39.(1)3;2;(2)m=1.
40.(1)
(2)4
(3)或
41.(1)a=4,b=6;
(2)△CPQ是等腰直角三角形.
42.
期中真题专项复习04 解答题
一、解答题
1.(2024八下·江苏期中)在平面直角坐标系中,矩形OACB的顶点O在坐标原点,顶点A、B分别在x轴、y轴的正半轴上,OA=3,OB=4,D为OB的中点,点E为边OA上的一个动点.
(1)求线段CD所在直线的解析式;
(2)当△CDE的周长最小时,求此时点E的坐标;
(3)当点E为OA中点时,坐标平面内,是否存在点F,使以D、E、C、F为顶点的四边形是平行四边形?若存在,请直接写出F点的坐标;若不存在,请说明理由.
2.(2024八下·泰兴期中)某中学组织学生到离学校15km的东山游玩,先遣队与大队同时出发,先遣队的速度是大队的速度的1.2倍,结果先遣队比大队早到0.5h,先遣队的速度是多少?大队的速度是多少?
3.(2024八下·苏州工业园期中)如图所示,点是反比例函数图象上的一点,轴于点,点是反比例函数图象上的一个动点,且.
(1)直接写出不等式中的范围______.
(2)求点的坐标.
4.(2024八下·盐城期中)在一个不透明的袋子中装有9个红球和6个黄球,这些球除颜色外都相同,将袋子中的球充分摇匀后,随机摸出一球.
(1)分别求出摸出的球是红球和黄球的概率.
(2)为了使摸出两种球的概率相同,再放进去7个同样的红球或黄球,那么这7个球中红球和黄球的数量分别应是多少?
5.(2024八下·淮安期中)如图,反比例函数的图象与一次函数的图象交于点,.
(1)若,求与的值;
(2)关于的不等式的解集为______;
(3)连接,,若的面积为12,则的值为______.
6.(2024八下·南京期中)如图,正方形ABCD的边长为5,点E,F分别在AD,DC上,AE=DF=2,BE与AF相交于点G,H为BF的中点,连接GH,求GH的长.
7.(2024八下·淮阴期中)随着通讯技术迅猛发展,人与人之间的沟通方式更多样、便捷,为此,孙老师设计了“5种你最喜欢的沟通方式”调查问卷(每人必选且只选一种)进行调查.将统计结果绘制成下面两幅不完整的统计图,其中A:电话,B:短信,C:微信,D:,E:其它.请结合图中所给的信息解答下列问题:
(1)这次参与调查的共有 人;将条形统计图补充完整;
(2)在扇形统计图中,表示“C:微信”的扇形圆心角的度数为 ;
(3)如果我国有13亿人在使用手机,请估计最喜欢用“微信”进行沟通的人数.
8.(2024八下·南通期中)如图,在平面直角坐标系中,四边形是平行四边形,为坐标原点,点A的坐标是,线段交轴于点,点的坐标是,线段,动点从点出发,沿射线的方向以每秒2个单位的速度运动,同时动点从点出发,以每秒1个单位的速度向终点运动,当点运动到点时,点随之停止运动,运动时间为秒.
(1)用t的代数式表示:_______,_______;
(2)若以为顶点的四边形是平行四边形时,求的值;
(3)若为等腰三角形,直接写出的值.
9.(2024八下·南通期中)某小区有一块长方形绿地,长为米,宽为米,现在要在长方形绿地中修建两个形状大小相同的小长方形花坛(即图中阴影部分),每个小长方形花坛的长为米,宽为米.
(1)求长方形绿地的周长;
(2)除花坛外,其他地方全修建成通道,通道需铺上造价为55元/平方米的地砖,则购买地砖需要多少钱?
10.(2024八下·丹徒期中)在一个不透明的袋子中装有仅颜色不同的12个小球,其中红球4个,黑球8个.
(1)进行如下的实验操作:先从袋子中取出个红球后,再从袋子中剩余的球中随机摸出1个球,此时将“第二次摸出的1个球是黑球”记为事件A.
①若事件A是必然事件,则m的值是______;
②若事件A是随机事件,则m的值是_____;
(2)从袋子中取出n个红球,再从袋子中剩余的球中随机摸出1个球,若第二次摸到的1个球是黑球的可能性大小是,求n的值.
11.(2024八下·姑苏期中)如图,直线:与轴、轴分别交于点,与直线:交与点.
(1)点的坐标为______(用含的代数式表示);
(2)点在轴上,横坐标为,点为直线上一点,当以为顶点的四边形为平行四边形时,且面积为时,求点的坐标;
(3)作点关于直线的对称点,当点落在直线上时,求点到直线的距离.
12.(2024八下·姑苏期中)如图,正方形,边长为,动点从点以每秒的速度沿向运动,动点从点以每秒的速度沿向运动,连结.两点同时出发,设运动时间为秒.
(1)求运动时间为何值时的面积为;
(2)连结、,是否存在某一时刻,使为等腰三角形,若存在,求出所有的值;若不存在,请说明理由.
13.(2024八下·姑苏期中)不透明的袋中有若干个红球和黑球,每个球除颜色外无其他差别.现从袋中随机摸出1个球,记下颜色后放回并搅匀,经过大量重复试验发现摸到黑球的频率逐渐稳定在附近.
(1)估计摸到黑球的概率是________;
(2)如果袋中的黑球有8个,求袋中共有几个球;
(3)在(2)的条件下,又放入个黑球,再经过大量重复试验发现摸到黑球的频率逐渐稳定在附近,直接写出的值.
14.(2024八下·江阴期中)如图,在直角坐标系中,,,一次函数的图象与x轴交于A点.
(1)A点坐标为 ;
(2)一次函数图象上是否存在一点C,使得四边形是平行四边形?如存在,求出C点坐标.若不存在,说明理由;
(3)将绕点O顺时针旋转,旋转得,问:能否使以点O、、D、为顶点的四边形是平行四边形?若能,求点的坐标;若不能,请说明理由.
15.(2024八下·无锡期中)在如图所示的平面直角坐标系中,正方形边长为2,点C的坐标为.
(1)如图1,动点D在边上,将沿直线折叠,点B落在点处,连接并延长,交于点E.
①当时,点D的坐标是______;
②若点E是线段的中点,求此时点D与点的坐标;
(2)如图2,动点D,G分别在边上,将四边形沿直线折叠,使点B的对应点始终落在边上(点不与点O,A重合),点C落在点处,交于点E.设,四边形的面积为S,直接写出S与t的关系式.
16.(2024八下·宜兴期中)我校在开学前去商场购进A,B两种品牌的乒乓球拍,购买A品牌球拍共花费1800元,购买B品牌球拍共花费700元,且购买A品牌球拍数量是购买B品牌球拍的3倍,已知购买一副B品牌球拍比购买一副A品牌球拍多花5元.
(1)求购买一副A品牌、一副B品牌球拍各需多少元?
(2)为了进一步发展“校园乒乓球”,学校在开学后再次购进了A,B两种品牌的球拍,每种品牌的球拍都不少于16副,在购买时,商场对两种品牌的球拍的销售单价进行了调整,A品牌球拍销售单价比第一次购买时提高了5%,B品牌球拍按第一次购买时销售单价的6折出售且总花费恰好为903元,那么此次有哪些购买方案?
17.(2024八下·广陵期中)在平面直角坐标系中,定义:横坐标与纵坐标均为整数的点为整点.如图,已知双曲线经过点,在第一象限内存在一点,满足.
(1)求的值
(2)如图1,过点分别作平行于轴,轴的直线,交双曲线于点,记为线段、双曲线所围成的区域为(含边界),
①当时,区域的整点个数为 ;
②当区域的整点个数为4时,点横坐标满足,则纵坐标取值范围为 ;
(3)直线将分成两部分,直线上方(不包含直线)区域记为,直线下方(不包含直线)区域记为,当的整点个数之差不超过2时,则的取值范围为 .
18.(2024八下·南京期中)某商场设立了一个可以自由转动的转盘,并做如下规定:顾客购物80元以上就获得一次转动转盘的机会,当转盘停止时,指针落在哪一区域就可以获得相应的奖品,下表是活动进行中的一组统计数据.
转动转盘的次数 100 150 200 500 800 1000
落在“洗衣粉”区域的次数 68 111 136 345 564 701
落在“洗衣粉”区域的频率 0.68 a 0.68 0.69 b 0.70
(1) , ;
(2)转动该转盘一次,获得洗衣粉的概率的估计值是多少
19.(2024八下·鼓楼期中)如图,平面直角坐标系xOy中,点O为坐标原点,四边形OABC为矩形,A(10,0),C(0,4),点D是OA的中点,点P在边BC上以每秒1个单位长的速度由点C向点B运动.
(1)当t= 时,四边形PODB是平行四边形;
(2)在线段PB上是否存在一点Q,使得四边形ODQP为菱形?若存在,求出当四边形ODQP为菱形时t的值,并求出Q点的坐标;若不存在,请说明理由;
(3)当△OPD为等腰三角形时,写出点P的坐标 (直接写出答案).
20.(2024八下·江阴期中)如图,在平面直角坐标系中,直线交轴于点,交轴于点,直线经过点且交轴正半轴于点,已知.
(1)点的坐标是 ,直线的表达式是 .
(2)若点为线段上一点,且满足,点为直线上一动点,在轴上是否存在点,使以点为顶点的四边形为平行四边形?如存在,请直接写出点的坐标;若不存在,说明理由.
(3)点为线段中点,点为轴上一动点,以为直角边作等腰直角,当点落在直线上时,求点的坐标.
21.(2024八下·淮安期中)如图,在矩形ABCD中,AC、BD相交于点O,DE⊥AC于点E.若,求∠CDE的度数.
22.(2024八下·苏州期中)已知矩形中,,的垂直平分线分别交于点E、F,垂足为O.
(1)如图1,连接,直接写出的长 ;
(2)如图2,动点P、Q分别从A、C两点同时出发,沿 和各边匀速运动一周.即点P自A→F→B→A停止,点Q自C→D→E→C停止.在运动过程中:
①已知点P的速度为每秒,点Q的速度为每秒,运动时间为t秒,当以A、P、C、Q四点为顶点的四边形是平行四边形时,求t的值;
②若点P、Q的运动路程分别为a、b(单位:cm,),以A、C、P、Q四点为顶点的四边形是平行四边形,求a与b满足的数量关系式.
23.(2024八下·苏州期中)如图,在中,,平分交于点D,点F在上,连接,E为的中点,交于点G,连接.
(1)若,求的长;
(2)若点F在直线上,当时,求的长.
24.(2024八下·苏州期中)如图,已知, 是一次函数图像与反比例函数图像的两个交点.
(1)求反比例函数和一次函数的解析式;
(2)求直线与轴的交点的坐标及的面积;
(3)请结合图像直接写出不等式的解集为 .
25.(2024八下·苏州期中)已知是的反比例函数,且当时,.
(1)直接写出函数与之间的关系式为 ;
(2)借助函数图象,求当时,的取值范围.
26.(2024八下·苏州期中)已知反比例函数的图象经过点.
(1)求反比例函数表达式;
(2)若点在该函数图象上,求m的值.
27.(2024八下·苏州工业园期中)在正方形中,是的中点,点从点出发沿的路线匀速运动,移动到点时停止.
(1)如图1,若正方形的边长为12,点的运动速度为2单位长度/秒,设秒时,正方形与重叠部分的面积为.
①当时,______;当时,______.
②求为何值时,以点为顶点的四边形是平行四边形?
(2)如图2,若点从出发沿的路线匀速运动.两点同时出发,点的速度大于点的速度,当到终点时,也停止运动.设秒时,正方形与(包括边缘及内部)重叠部分的面积为,与的函数图象如图3所示.
①,两点在第______秒相遇;正方形的边长是______.
②点的速度为______单位长度/秒;点的速度为______单位长度/秒.
③当为何值时,重叠部分面积等于32?
28.(2024八下·淮阴期中)如图,矩形的对角线、相交于点O,,cm.
(1)求的度数;
(2)求矩形对角线的长.
29.(2024八下·涟水期中)在矩形中,相交于点,平分,交于点.若,求的度数.
30.(2024九上·温州期中)在一只不透明的口袋里,装有若干个除了颜色外均相同的小球,某数学学习小组做摸球试验,将球搅匀后从中随机摸出一个球记下颜色,再把它放回袋中,不断重复.如下表是活动进行中的一组统计数据:
摸球的次数
摸到白球的次数
摸到白球的频率
(1)上表中的________,________;
(2)“摸到白球的”的概率的估计值是________(精确到);
(3)如果袋中有个白球,那么袋中除了白球外,还有________个其它颜色的球.
31.(2024八下·昆山期中)如图,在四边形ABCD中,,,,,.动点M从点B出发沿边以速度向终点C运动;同时动点N从点D出发,以速度沿射线运动,当点M到达终点时,点N也随之停止运动,设点M运动的时间为.
(1)当时,__________;
(2)是否存在t的值,使得A,B,M,N为顶点的四边形为平行四边形?若存在,求出t的值;若不存在,请说明理由;
(3)若动点M关于直线对称的点恰好落在直线上,请直接写出t的值.
32.(2024八下·昆山期中)定义:若点A在一个函数图象上,且点A的横、纵坐标相等,则称点A为这个函数的“等点”.
(1)关于“等点”,下列说法正确的有__________;
①函数有两个“等点”;②函数有一个“等点”;③函数没有“等点”.
(2)已知反比例函数与一次函数的图象上有同一个“等点”,求反比例函数的表达式;
(3)函数的图象上有两个“等点”A、B,设A、B两点之间的距离为m,若,则k的取值范围是__________.
33.(2024八下·昆山期中)如图,点A是反比例函数图象上一点,过点A作y轴的平行线,交函数的图象于点B,连接,交反比例函数的图象于点C,已知.
(1)求k的值;
(2)连接,若点A的横坐标为4,求的面积.
34.(2024八下·昆山期中)解分式方程:
35.(2024八下·扬州期中)已知关于的分式方程
(1)若该方程的增根为,求的值;
(2)若该方程有增根,求的值.
(3)若该方程无解,求的值.
36.(2024八下·盐都期中)如图,在矩形ABCD中,AB=4,BC=5,延长BC到点E,使CE=3,连接DE.动点P从点B出发,以每秒2个单位的速度沿折线BC-CD向终点D运动,设点P运动的时间为t秒.(t>0)
(1)DE=______;
(2)连接AP,当四边形APED是菱形时,求菱形APED的周长;
(3)连接BP、PD,设四边形ABPD的面积为S,求S与t之间的函数关系式;
(4)直接写出点P到四边形ABED相邻两边距离相等时t的值.
37.(2024八下·盐都期中)如图,已知四边形是正方形,、分别是和的延长线上的点,且,连接、、,
(1)填空:可以由绕旋转中心______点,按顺时针方向旋转______度得到;
(2)若,求四边形的面积.
38.(2024八下·吴江期中)如图,正比例函数与反比例函数的图像交于点,点是反比例函数图像上的点,连接.
(1)求,和的值;
(2)若点是正比例函数图像上的点,且的面积是4,求点的坐标.
39.(2024八下·镇江期中)在一个不透明的盒子中装有颜色不同的8个小球,其中红球3个,黑球5个.
(1)先从袋中取出m(m>1)个红球,再从袋中随机摸出1个球,将“摸出黑球”记为事件A.请完成下列表格:
事件A 必然事件 随机事件
m的值
(2)先从袋中取出m个红球,再放入m个一样的黑球并摇匀,随机摸出1个球是黑球的概率是,求m的值.
40.(2024八下·淮安期中)如图1,反比例函数与一次函数的图象交于点,点,一次函数与轴相交于点.
(1)求反比例函数和一次函数的表达式;
(2)连接,,求的面积;
(3)当时,x的范围为 .
41.(2024八下·扬州期中)如图,以矩形OABC的顶点O为坐标原点,边OA所在直线为x轴,OC所在直线为y轴,建立如图所示的直角坐标系,已知A(a,0),C(0,b),其中a,b满足|a-4|+(b-6)2=0,点P从点O出发沿OA以1cm/s的速度向点A移动,同时点Q从点B出发沿BA方向以1cm/s的速度向点A移动,设运动时间为t秒(0≤t≤4).
(1)求出a,b的值.
(2)当t=2时,判断△PCQ的形状,并说明理由.
42.(2024八下·扬州期中)如图,在中,的平分线交于点E,若,求、的度数.
答案解析部分
1.(1)直线 CD:;(2);(3)存在,或或
2.先遣队的速度是6km/h,大队的速度是5km/h
3.(1)或者
(2)点P的坐标是或
4.(1),;(2)2个和5个
5.(1),
(2)或
(3)9
6.
7.(1)2000;如图所示
(2)
(3)5.2亿人
8.(1);
(2)6或
(3)4或6或
9.(1)米
(2)3080元
10.(1)4;2或3
(2)2
11.(1);
(2)点的坐标为或;
(3).
12.(1)运动时间时的面积为
(2)或或或时,为等腰三角形
13.(1)
(2)
(3)
14.(1);
(2)存在,
(3)的坐标为或或.
15.(1)①;点D的坐标为,点的坐标为
(2)
16.(1)一副A品牌球拍需30元、一副B品牌球拍需35元
(2)有两个方案,方案一:购买18副A品牌球拍与16副B品牌球拍
方案二:购买16副A品牌球拍与19副B品牌球拍
17.(1)4
(2)①11;②
(3)
18.(1)0.74;0.705
(2)0.70
19.(1)t=5;(2)存在,t=3,点Q的坐标为(8,4);(3)P1(2,4),P2(2.5,4),P3(3,4),P4(8,4)
20.(1),;
(2)存在,点坐标为或;
(3)点坐标为或.
21.
22.(1)
(2)①;②
23.(1)
(2)
24.(1)反比例函数的解析式为,一次函数的解析式为
(2),的面积为
(3)或
25.(1)
(2)
26.(1);
(2)或.
27.(1)①114;60;②9秒
(2)①4秒;8;②4;2;③或6,
28.(1)
(2)2
29.
30.(1),
(2)
(3)除白球外,还有大约个其它颜色的小球
31.(1)
(2)或
(3)或
32.(1)①③
(2)
(3)
33.(1)
(2)
34.无解
35.(1)
(2)或
(3)或或
36.(1)5;
(2)20;
(3)S=;
(4)t=2或或.
37.(1)A,90
(2)64
38.(1),,
(2),
39.(1)3;2;(2)m=1.
40.(1)
(2)4
(3)或
41.(1)a=4,b=6;
(2)△CPQ是等腰直角三角形.
42.
同课章节目录
