期中真题专项复习02填空题(含答案)--2024-2025学年七年级数学下册(沪科版2024)
文档属性
| 名称 | 期中真题专项复习02填空题(含答案)--2024-2025学年七年级数学下册(沪科版2024) |  | |
| 格式 | docx | ||
| 文件大小 | 399.6KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-03-30 06:11:54 | ||
图片预览



文档简介
2024-2025学年七年级数学下册(沪科版2024)
期中真题专项复习02填空题
一、填空题
1.(2024七下·嘉定期中)在数轴上表示的点与表示数3的点之间的距离是 .
2.(2024七下·龙江期中)若a2=64,则= .
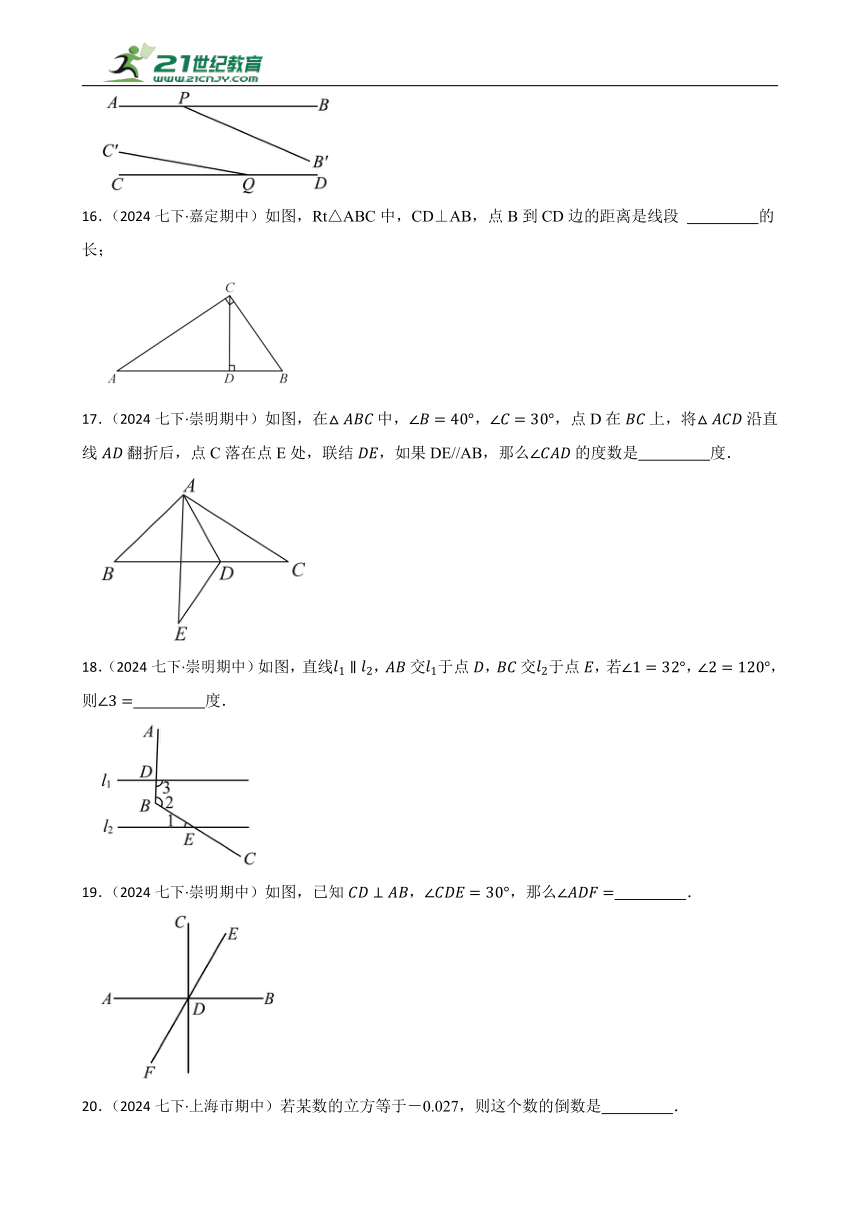
3.(2024七下·普陀期中)计算: .
4.(2024七下·浦东期中)如图,直线与交于点平分,那么 °
5.(2024七下·上海市期中)若的整数部分为,小数部分为,则的值为 .
6.(2024七下·黄浦期中)如图,直线、相交于点,于,,= °.
7.(2024七下·柯桥期中)如果(x+3)(x+a)=x2﹣2x﹣15,则a= .
8.(2024七下·宝山期中)如图:两条平行直线、直线所截,,,则 .
9.(2024七下·普陀期中)比较大小:﹣4 (填“>”、“=”或“<”).
10.(2024七下·虹口期中)如图, 已知, 点M、N分别是直线上的点, 点E、F在之间, 且位于的两侧,分别平分与, 点 G 在 内部, 且 ,如果, 那么的度数为 .(用含的代数式表示)
11.(2024七下·上海市期中)如图,,,点B到边的距离是线段 的长.
12.(2024七下·宝山期中)如图,直线与相交于点O,,则直线与的夹角为 度.
13.(2024七下·宝山期中)计算: .
14.(2024七下·普陀期中)如图,直线,将一个含有角的直角三角尺放置在如图所示的位置,如果,那么 .
15.(2024七下·嘉定期中)已知直线,点P、Q分别在上,如图所示,射线按顺时针方向以每秒的速度旋转至便立即回转,并不断往返旋转;射线按顺时针方向每秒旋转至停止,此时射线也停止旋转.
(1)若射线同时开始旋转,当旋转时间30秒时,与的位置关系为 ;
(2)若射线先转45秒,射线才开始转动,当射线旋转的时间为 秒时,.
16.(2024七下·嘉定期中)如图,Rt△ABC中,CD⊥AB,点B到CD边的距离是线段 的长;
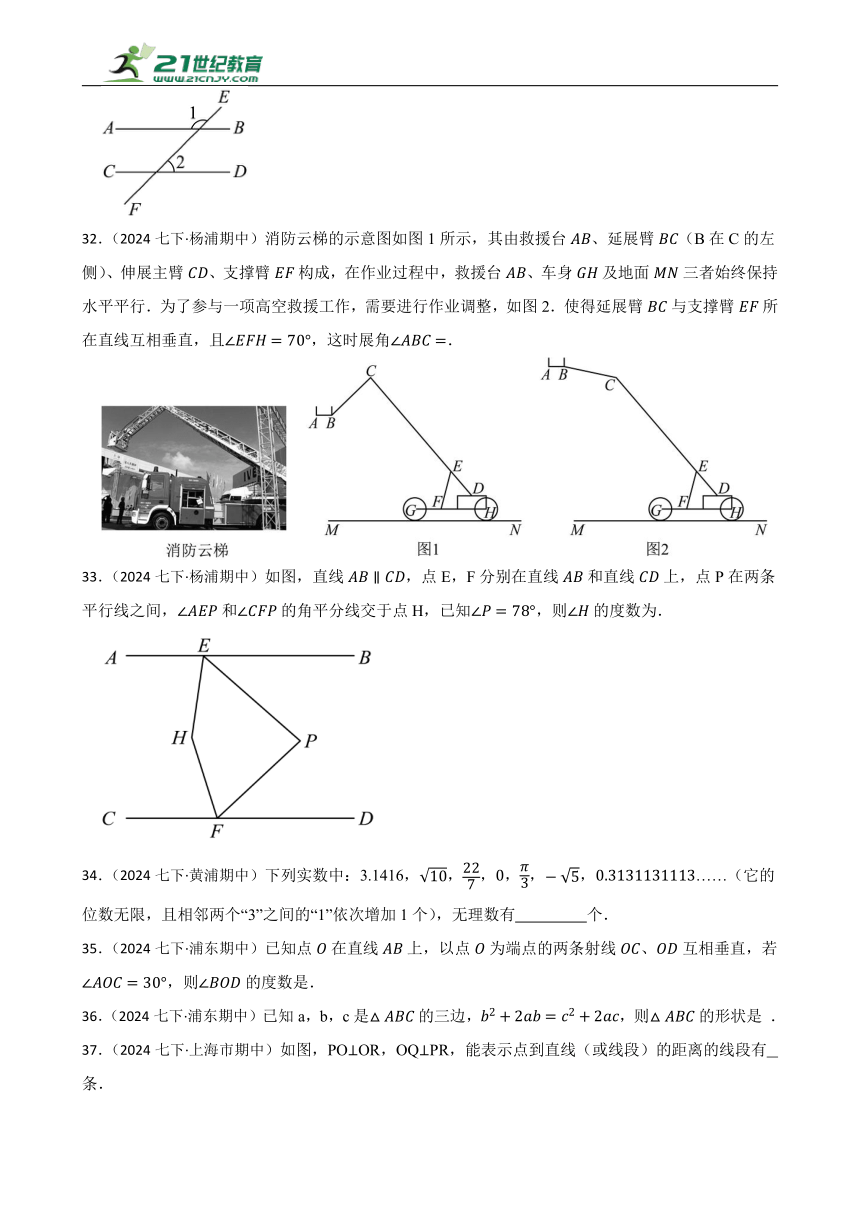
17.(2024七下·崇明期中)如图,在中,,,点D在上,将沿直线翻折后,点C落在点E处,联结,如果DE//AB,那么的度数是 度.
18.(2024七下·崇明期中)如图,直线,交于点,交于点,若,,则 度.
19.(2024七下·崇明期中)如图,已知,,那么 .
20.(2024七下·上海市期中)若某数的立方等于-0.027,则这个数的倒数是 .
21.(2024七下·崇明期中)已知16的平方根是,,那么 .
22.(2024七下·虹口期中)如图, 在中, , 点D是边上一点, 将 沿翻折,点C落在点E处, 如果, 那么 .
23.(2024七下·静安期中),那么整数;
24.(2024七下·普陀期中)如图,已知,点E在线段的延长线上,平分,连接,如果,那么 °.
25.(2024七下·上海市期中)已知点A为直线上一点,点B在直线外,且A、B两点之间的距离是,如果点B到直线的距离是x,那么x的取值范围是 .
26.(2024七下·普陀期中)计算: .
27.(2024七下·普陀期中)在数轴上,点A、点B所对应的数分别是和,那么A、B两点的距离为 .
28.(2024七下·静安期中)两直线相交于点,若,则两直线的夹角为度.
29.(2024七下·合肥期中)我们知道,负数没有平方根,但对于三个互不相等的负整数,若两两乘积的算术平方根都是整数,则称这三个数为“开心组合数”.例如:,,这三个数,,,,其结果,,都是整数,所以,,这三个数为“开心组合数”.若三个数,,是“开心组合数”,其中有两个数乘积的算术平方根为,那么 .
30.(2024七下·上海市期中)计算: = ; = .
31.(2024七上·上海市期中)如图,已知,,,,的度数为 .
32.(2024七下·杨浦期中)消防云梯的示意图如图1所示,其由救援台、延展臂(B在C的左侧)、伸展主臂、支撑臂构成,在作业过程中,救援台、车身及地面三者始终保持水平平行.为了参与一项高空救援工作,需要进行作业调整,如图2.使得延展臂与支撑臂所在直线互相垂直,且,这时展角.
33.(2024七下·杨浦期中)如图,直线,点E,F分别在直线和直线上,点P在两条平行线之间,和的角平分线交于点H,已知,则的度数为.
34.(2024七下·黄浦期中)下列实数中:3.1416,,,,,,……(它的位数无限,且相邻两个“3”之间的“1”依次增加1个),无理数有 个.
35.(2024七下·浦东期中)已知点在直线上,以点为端点的两条射线、互相垂直,若,则的度数是.
36.(2024七下·浦东期中)已知a,b,c是的三边,,则的形状是 .
37.(2024七下·上海市期中)如图,POOR,OQPR,能表示点到直线(或线段)的距离的线段有 条.
38.(2024七下·浦东期中)如图,已知,平分,,那么.
39.(2024七下·浦东期中)已知直线和直线交于点比它的邻补角的2倍少,则直线与直线的夹角是度.
40.(2024七下·浦东期中)的算术平方根减去的立方根的差为.
41.(2024七下·浦东期中)在数,,,,,,中,无理数有.
42.(2024七下·静安期中)定义:如果一个正整数能表示为两个正整数的平方差,且,则称这个正整数为“智慧优数”.例如,,16就是一个智慧优数,可以利用进行研究.若将智慧优数从小到大排列,第9个智慧优数是.
43.(2024七下·静安期中)若实数满足等式,则化简.
44.(2024七下·静安期中)如图,的面积等于,则点到直线的距离为.
45.(2024七下·上海市期中)下列各数、、、、、、(1和1之间每一个间隔就多一个0)、、,其中无理数的个数是 .
46.(2023七下·松江期中)如图,一共有 对同旁内角.
47.(2024七下·静安期中)如图,直线相交于点,如果平分,那么度度数为.
48.(2024七下·上海市期中)实数a的立方根是3,那么 .
49.(2024七下·上海市期中)10的平方根是 .
50.(2024七上·上海市期中)如果,那么称为的“拉格数”,记为由定义可知:.如,则,给出下列关于“拉格数”的结论:
①,②,③,④,⑤
其中正确的结论有 .
答案解析部分
1.
2.±2
解:∵a2=64,
∴a=±8,
∴=±2
故填±2.
先根据平方根的定义求出a的值,再利用立方根的定义求出的值.
3.4
4.
5.
6.60
7.﹣5
解:(x+3)(x+a)=x2+(a+3)x+3a=x2﹣2x﹣15,
可得:a+3=﹣2,
解得:a=﹣5.
故答案为:﹣5.
已知等式左边利用多项式乘多项式法则计算,合并后利用多项式相等的条件即可求出a的值.
8.
9.>
10.
11.
12.
13.
14.
15.;15或63或135
16.BD
17.40
18.
19.
20.
21.或
22.25
23.3
24.15
25.
26.
27.
28.
29.
30.0.75;-0.01
31.
32.
33.
34.4
35.或
36.等腰三角形
37.5.
38.
39.
40.
41.,
42.
43.
44.
45.2
46.
解:如图所示:同旁内角有:∠A和∠D,∠D和∠C,∠C和∠B,∠B和∠A,
∴一共有4对同旁内角,
故答案为:4.
两条直线被第三条直线所截,在截线同旁,且在被截线之内的两角,叫做同旁内角。根据同旁内角的定义,结合图形,判断求解即可。
47.
48.
49.
50.②③④
期中真题专项复习02填空题
一、填空题
1.(2024七下·嘉定期中)在数轴上表示的点与表示数3的点之间的距离是 .
2.(2024七下·龙江期中)若a2=64,则= .
3.(2024七下·普陀期中)计算: .
4.(2024七下·浦东期中)如图,直线与交于点平分,那么 °
5.(2024七下·上海市期中)若的整数部分为,小数部分为,则的值为 .
6.(2024七下·黄浦期中)如图,直线、相交于点,于,,= °.
7.(2024七下·柯桥期中)如果(x+3)(x+a)=x2﹣2x﹣15,则a= .
8.(2024七下·宝山期中)如图:两条平行直线、直线所截,,,则 .
9.(2024七下·普陀期中)比较大小:﹣4 (填“>”、“=”或“<”).
10.(2024七下·虹口期中)如图, 已知, 点M、N分别是直线上的点, 点E、F在之间, 且位于的两侧,分别平分与, 点 G 在 内部, 且 ,如果, 那么的度数为 .(用含的代数式表示)
11.(2024七下·上海市期中)如图,,,点B到边的距离是线段 的长.
12.(2024七下·宝山期中)如图,直线与相交于点O,,则直线与的夹角为 度.
13.(2024七下·宝山期中)计算: .
14.(2024七下·普陀期中)如图,直线,将一个含有角的直角三角尺放置在如图所示的位置,如果,那么 .
15.(2024七下·嘉定期中)已知直线,点P、Q分别在上,如图所示,射线按顺时针方向以每秒的速度旋转至便立即回转,并不断往返旋转;射线按顺时针方向每秒旋转至停止,此时射线也停止旋转.
(1)若射线同时开始旋转,当旋转时间30秒时,与的位置关系为 ;
(2)若射线先转45秒,射线才开始转动,当射线旋转的时间为 秒时,.
16.(2024七下·嘉定期中)如图,Rt△ABC中,CD⊥AB,点B到CD边的距离是线段 的长;
17.(2024七下·崇明期中)如图,在中,,,点D在上,将沿直线翻折后,点C落在点E处,联结,如果DE//AB,那么的度数是 度.
18.(2024七下·崇明期中)如图,直线,交于点,交于点,若,,则 度.
19.(2024七下·崇明期中)如图,已知,,那么 .
20.(2024七下·上海市期中)若某数的立方等于-0.027,则这个数的倒数是 .
21.(2024七下·崇明期中)已知16的平方根是,,那么 .
22.(2024七下·虹口期中)如图, 在中, , 点D是边上一点, 将 沿翻折,点C落在点E处, 如果, 那么 .
23.(2024七下·静安期中),那么整数;
24.(2024七下·普陀期中)如图,已知,点E在线段的延长线上,平分,连接,如果,那么 °.
25.(2024七下·上海市期中)已知点A为直线上一点,点B在直线外,且A、B两点之间的距离是,如果点B到直线的距离是x,那么x的取值范围是 .
26.(2024七下·普陀期中)计算: .
27.(2024七下·普陀期中)在数轴上,点A、点B所对应的数分别是和,那么A、B两点的距离为 .
28.(2024七下·静安期中)两直线相交于点,若,则两直线的夹角为度.
29.(2024七下·合肥期中)我们知道,负数没有平方根,但对于三个互不相等的负整数,若两两乘积的算术平方根都是整数,则称这三个数为“开心组合数”.例如:,,这三个数,,,,其结果,,都是整数,所以,,这三个数为“开心组合数”.若三个数,,是“开心组合数”,其中有两个数乘积的算术平方根为,那么 .
30.(2024七下·上海市期中)计算: = ; = .
31.(2024七上·上海市期中)如图,已知,,,,的度数为 .
32.(2024七下·杨浦期中)消防云梯的示意图如图1所示,其由救援台、延展臂(B在C的左侧)、伸展主臂、支撑臂构成,在作业过程中,救援台、车身及地面三者始终保持水平平行.为了参与一项高空救援工作,需要进行作业调整,如图2.使得延展臂与支撑臂所在直线互相垂直,且,这时展角.
33.(2024七下·杨浦期中)如图,直线,点E,F分别在直线和直线上,点P在两条平行线之间,和的角平分线交于点H,已知,则的度数为.
34.(2024七下·黄浦期中)下列实数中:3.1416,,,,,,……(它的位数无限,且相邻两个“3”之间的“1”依次增加1个),无理数有 个.
35.(2024七下·浦东期中)已知点在直线上,以点为端点的两条射线、互相垂直,若,则的度数是.
36.(2024七下·浦东期中)已知a,b,c是的三边,,则的形状是 .
37.(2024七下·上海市期中)如图,POOR,OQPR,能表示点到直线(或线段)的距离的线段有 条.
38.(2024七下·浦东期中)如图,已知,平分,,那么.
39.(2024七下·浦东期中)已知直线和直线交于点比它的邻补角的2倍少,则直线与直线的夹角是度.
40.(2024七下·浦东期中)的算术平方根减去的立方根的差为.
41.(2024七下·浦东期中)在数,,,,,,中,无理数有.
42.(2024七下·静安期中)定义:如果一个正整数能表示为两个正整数的平方差,且,则称这个正整数为“智慧优数”.例如,,16就是一个智慧优数,可以利用进行研究.若将智慧优数从小到大排列,第9个智慧优数是.
43.(2024七下·静安期中)若实数满足等式,则化简.
44.(2024七下·静安期中)如图,的面积等于,则点到直线的距离为.
45.(2024七下·上海市期中)下列各数、、、、、、(1和1之间每一个间隔就多一个0)、、,其中无理数的个数是 .
46.(2023七下·松江期中)如图,一共有 对同旁内角.
47.(2024七下·静安期中)如图,直线相交于点,如果平分,那么度度数为.
48.(2024七下·上海市期中)实数a的立方根是3,那么 .
49.(2024七下·上海市期中)10的平方根是 .
50.(2024七上·上海市期中)如果,那么称为的“拉格数”,记为由定义可知:.如,则,给出下列关于“拉格数”的结论:
①,②,③,④,⑤
其中正确的结论有 .
答案解析部分
1.
2.±2
解:∵a2=64,
∴a=±8,
∴=±2
故填±2.
先根据平方根的定义求出a的值,再利用立方根的定义求出的值.
3.4
4.
5.
6.60
7.﹣5
解:(x+3)(x+a)=x2+(a+3)x+3a=x2﹣2x﹣15,
可得:a+3=﹣2,
解得:a=﹣5.
故答案为:﹣5.
已知等式左边利用多项式乘多项式法则计算,合并后利用多项式相等的条件即可求出a的值.
8.
9.>
10.
11.
12.
13.
14.
15.;15或63或135
16.BD
17.40
18.
19.
20.
21.或
22.25
23.3
24.15
25.
26.
27.
28.
29.
30.0.75;-0.01
31.
32.
33.
34.4
35.或
36.等腰三角形
37.5.
38.
39.
40.
41.,
42.
43.
44.
45.2
46.
解:如图所示:同旁内角有:∠A和∠D,∠D和∠C,∠C和∠B,∠B和∠A,
∴一共有4对同旁内角,
故答案为:4.
两条直线被第三条直线所截,在截线同旁,且在被截线之内的两角,叫做同旁内角。根据同旁内角的定义,结合图形,判断求解即可。
47.
48.
49.
50.②③④
同课章节目录
