期中真题专项复习04 解答题(含答案)--2024-2025学年八年级数学下册(沪科版2024)
文档属性
| 名称 | 期中真题专项复习04 解答题(含答案)--2024-2025学年八年级数学下册(沪科版2024) |

|
|
| 格式 | docx | ||
| 文件大小 | 956.3KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-03-30 00:00:00 | ||
图片预览




文档简介
2024-2025学年八年级数学下册(沪科版2024)
期中真题专项复习04 解答题
一、解答题
1.(2024八下·濉溪期末)周末,小明和小亮去汉风公园放风筝,为了测得风筝的垂直高度,他们进行了如下操作:
测得水平距离的长为米;
根据手中剩余线的长度计算出风筝线的长为米;
牵线放风筝的小明的身高为米.
(1)求风筝的垂直高度;
(2)如果小明想风筝沿方向下降米,则他应该往回收线多少米?
2.(2024八下·霍邱期末)已知关于的一元二次方程有两个不同的实数根.
(1)求的取值范围;
(2)若方程的两个根的差为2,求的值.
3.(2024八下·庐江期末)已知,如图,在平面直角坐标系中,直线分别交x轴于点A,交y轴于点B,线段的垂直平分线分别交x轴于点C,交y轴于点D,交于点E.
(1)求点E的坐标;
(2)求直线的解析式;
(3)平面内是否存在点F,使得以B、C、D、F为顶点的四边形是平行四边形,若存在,直接写出点F的坐标.
4.(2024八下·庐江期末)已知中,,,边上的高,求边的长.
5.(2024八下·合肥月考)已知关于x的一元二次方程 有两个实数根,.
(1)求的取值范围;
(2)当时,求的值.
6.(2024八下·萧县期末)如图所示,在平面直角坐标系中,的边在x轴上,点D在y轴上.已知,,,从C点出发的E点,以每秒2个单位长度的速度向D点移动.M是的中点,的延长线交于F点.
(1)求点B,C的坐标.
(2)当四边形是平行四边形时,求点E的移动时间t.
(3)当为等腰三角形时,直接写出点E的坐标______.
7.(2024七下·全椒期末)已知关于x的方程无实数根.
(1)求m的取值范围;
(2)判断方程的根的情况.
8.(2024八下·合肥期末)已知关于x 的一元二次方程x2 -5x + m = 0.
(1)若方程有实数根,求实数m 的取值范围;
(2)若方程两实数根为x1,x2,且满足3 x1-2x2 =5,求实数m 的值.
9.(2024八下·界首期末)国庆节时,某班一个数学小组,为庆祝祖国华诞,他们每两人之间互送贺卡一张,已知全组共送贺卡110张, 问这个小组一共有多少人?
10.(2024八下·安庆期末)已知关于的一元二次方程有两个实数根.
(1)求实数的取值范围;
(2)若,求的值.
11.(2024八下·浏阳期中)我国古代数学著作《九章算术》中的一个问题.原文是:今有池方一丈,葭生其中央,出水尺.引葭赴岸,适与岸齐问水深、葭长各几何译文大意是:如图,有一个水池,水面是一个边长为10尺的正方形,在水池正中央有一根芦苇,它高出水面1尺.如果把这根芦苇拉向水池边的中点,它的顶端恰好到达池边的水面.问水的深度与这根芦苇的长度分别是多少?
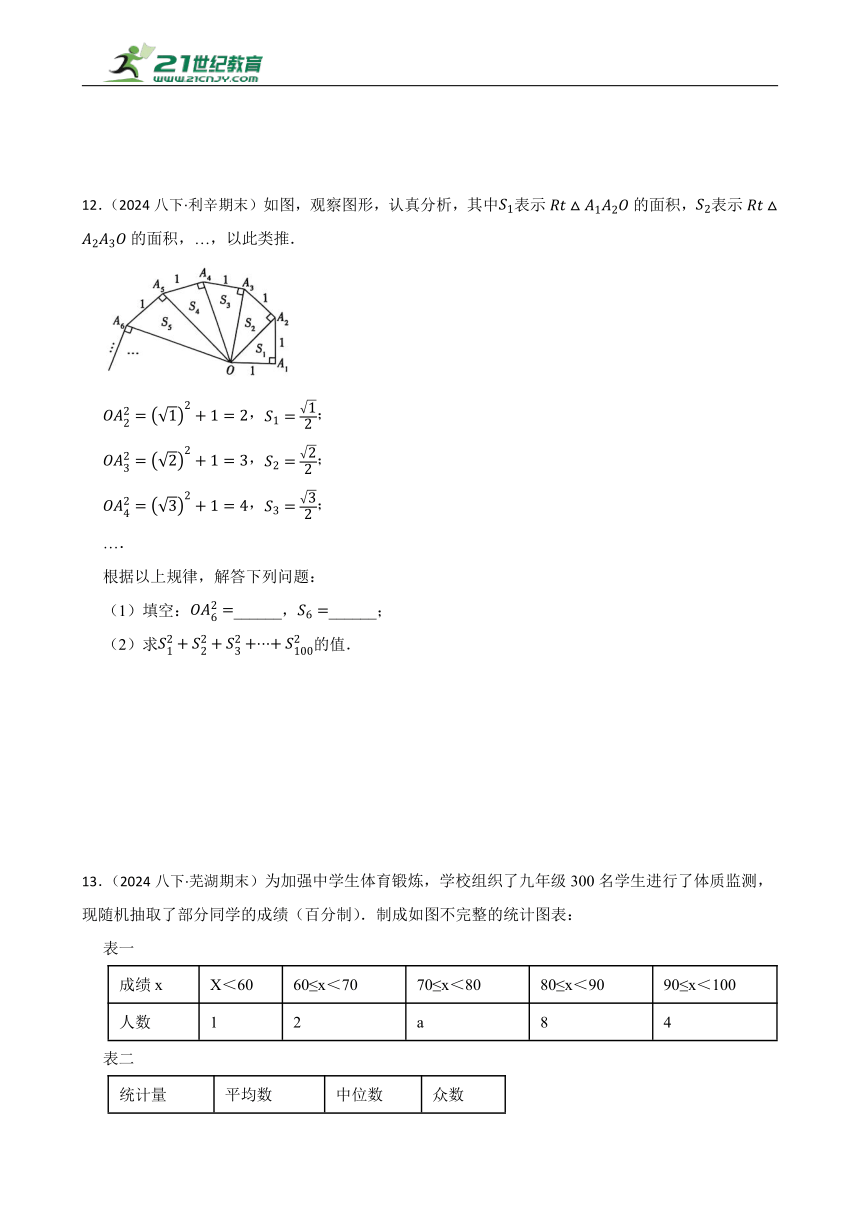
12.(2024八下·利辛期末)如图,观察图形,认真分析,其中表示的面积,表示的面积,…,以此类推.
,;
,;
,;
….
根据以上规律,解答下列问题:
(1)填空:______,______;
(2)求的值.
13.(2024八下·芜湖期末)为加强中学生体育锻炼,学校组织了九年级300名学生进行了体质监测,现随机抽取了部分同学的成绩(百分制).制成如图不完整的统计图表:
表一
成绩x X<60 60≤x<70 70≤x<80 80≤x<90 90≤x<100
人数 1 2 a 8 4
表二
统计量 平均数 中位数 众数
成绩 79.7 b 72
根据以上信息回答下列问题:
(1)若抽取的学生成绩处在80≤x<90这一组的数据如下:
88 87 81 80 82 88 84 86
根据以上数据将表一和表二补充完整:a ;b ;
(2)在扇形统计图中,表示问卷成绩在70≤x<80这一组的扇形圆心角度数为 ;
(3)若成绩在80分及以上为体质达标,请你估计该校九年级一共有多少名学生的体质达标?
14.(2024八下·霍邱期末)甲,乙两个小区各有户居民,为了解两个小区3月份用户使用燃气量情况,小明和小丽分别从中随机抽取30户进行调查,并对数据进行整理、描述和分析.下面给出了部分信息.
a.甲小区用气量频数分布表如下:
分组
频数 3 6 10 3
b.乙小区用气量频数分布直方图如下(数据分成5组:,,,,)
c.乙小区用气量的数据在这一组的是:
d.甲,乙两小区用气量的平均数、中位数、众数如下:
小区 平均数 中位数 众数
甲
乙
根据以上信息,回答下列问题:
(1)写出表中m和n的值;
(2)在甲小区抽取的用户中,记3月份用气量高于他们的平均用气量的户数为.在乙小区抽取的用户中,记3月份用气量高于他们的平均用气量的户数为.比较,的大小,并说明理由;
(3)估计甲乙两小区中用气量不小于20立方米的总户数.
15.(2024八下·澧县期中)看着冉冉升起的五星红旗,你们是否想过旗杆到底有多高呢?某数学兴趣小组为了测量旗杆高度,进行以下操作:如图1,先将升旗的绳子拉到旗杆底端,发现绳子末端刚好接触到地面;如图2,再将绳子末端拉到距离旗杆8m处,发现绳子末端距离地面2m.请根据以上测量情况,计算旗杆的高度.
16.(2024八下·霍邱期末)如图,在四边形中,,,,,求的长.
17.(2024八下·庐阳期中)某公园准备在一块长为,宽为的长方形花园内修建一个底部为正方形的温室花房(如图所示),在温室花房四周修四条宽度相同,且与温室花房各边垂直的小路,温室花房边长是小路宽度的倍,花园内其他的空白地方铺草坪,设小路宽度为.
(1)用含的代数式分别表示花园内温室花房的面积和小路面积;
(2)若草坪面积为时,求这时道路宽度.
18.(2024八下·庐阳期中)若关于的方程有实数根,求的取值范围.
19.(2024八下·庐阳期中)解方程:3x2﹣2x﹣1=0.
20.(2024八下·涡阳期中)已知,
(1)求的值;
(2)若的小数部分为m,的小数部分为n,求的值.
21.(2024八下·庐江期中)如图,在四边形中,,,对角线,交于点,平分,过点作交的延长线于点,连接.
(1)求证:四边形是菱形;
(2)若,求的长;
(3)在(2)的条件下,已知点是线段上一点,且,求的长.
22.(2024八下·庐江月考)如图,四边形是平行四边形,点,分别为线段,的中点.若,求的度数.
23.(2024八下·池州月考)如图,有一张四边形纸片ABCD,AB⊥BC.经测得AB=9cm,BC=12cm,CD=8cm,AD=17cm.
(1)求A、C两点之间的距离.
(2)求这张纸片的面积.
24.(2024八下·池州月考)如图,在正方形中,点分别是边的中点,相交于点,连接.
(1)若,则的度数是 ;
(2)连接,则与之间的位置关系是 .
25.(2024八下·安徽期末)关于的一元二次方程有两个不相等的实数根、.
(1)求的取值范围;
(2)若,求的值.
26.(2024八下·天长月考)如图,在矩形中,,点P与点Q同时出发,点P从点D出发向点A运动,运动到点A停止,点Q从点B出发向点C运动,运动到点C停止,点P,Q的速度都是,连接,设点P,Q的运动时间为.
(1)求当t为何值时,四边形是正方形;
(2)求当t为何值时,;
(3)当四边形的面积为时,求矩形的周长与四边形的周长的比值.
27.(2024八下·天长月考)如图,在边长为1个单位长度的小正方形组成的网格中,的顶点都在小正方形网格线的交点上.求的周长及边上的高.
28.(2024八下·合肥期末)观察下列等式:
第1个等式:;
第2个等式:;
第3个等式:,
……
按照以上规律,解决下列问题.
(1)写出第4个等式:______.
(2)写出你猜想的第n个等式(用含n的等式表示).
(3)请用(2)中发现的规律计算:.
29.(2024八下·庐江期中)
(1)如图1,在四边形中,与相交于点,,,分别是,的中点,连接,分别交,于点,,判断的形状,并说明理由;
(2)如图2,在四边形中,,,分别是,的中点,连接并延长,分别与,的延长线交于点,.求证:.
30.(2024八下·庐江期中)如图,在平行四边形ABCD中,E,F分别为边AB,CD的中点,BD是对角线.
(1)求证:四边形DEBF是平行四边形;
(2)当DE平分∠ADB时,判断四边形DEBF是什么特殊的平行四边形,并说明理由.
31.(2024八下·庐江期中)在中,,,,求的面积.
某学习小组经过合作交流,给出了下面的解题思路,请你按照他们的解题思路完成解答过程.作于,设,用含的式子表示根据勾股定理,利用作为“桥梁”,建立方程模型求出利用勾股定理求出的长,再计算三角形的面积.
32.(2024九上·无锡月考)如图,由两个全等的和构成的四边形,已知直角三角形的直角边长分别为m、n,斜边长为q,分别以m,,n为二次项系数、一次项系数和常数项构造的一元二次方程,称为勾股方程.
(1)直接写出一个勾股方程;
(2)若勾股方程有两个相等的实数根,求的值;
(3)若是勾股方程的一个根,且四边形的周长是6,求四边形的面积.
33.(2024八下·合肥期中) 已知关于的一元二次方程.
(1)若方程有两个相等的实数根,求的值;
(2)若方程的两实数根之积等于,求的值.
34.(2024八下·蜀山期中)请阅读下面的过程,完成相应的题目:
的整数部分是1,故的小数部分是.
(1)的整数部分是______;
(2)设分别是的整数部分和小数部分,则______,______;
(3)在(2)的条件下,若已知,为有理数,且,求的值.
35.(2024八下·六安期中) 如图,将,的长方形,沿过顶点A的直线为折痕折叠,使顶点B落在边上的点Q处.
(1)求的长;
(2)求的长.
36.(2024八下·岳麓月考)如图,在笔直的铁路上A、B两点相距25km,C、D为两村庄,DA=10km,CB=15km,DA⊥AB于A,CB⊥AB于B,现要在AB上建一个中转站E,使得C、D两村到E站的距离相等.求E应建在距A多远处?
37.(2024八下·利辛期中)若是关于的一元二次方程的两个实数根.
(1)求的取值范围;
(2)若,求的值.
38.(2024八下·利辛期中)如图,把长方形沿对折后点落在边的点处,,,求:
(1)的长;
(2)的长.
39.(2024八下·潜山期中) 如图,四边形是证明勾股定理时用到的一个图形,a,b,c是和边长,易知,这时我们把关于x的形如的一元二次方程称为“勾系一元二次方程”.
请解决下列问题:
(1)当,时,写出该“勾系一元二次方程”;
(2)求证:关于x的“勾系一元二次方程”必有实数根;
(3)如图,若是“勾系一元二次方程”的一个根,且四边形的周长是,求的面积.
40.(2024八下·潜山期中) 如图,方格中小正方形的边长为1,的三个顶点都在小正方形的格点上,求∶
(1)请判断三角形是否是直角三角形,并说明理由;
(2) 的面积;
(3)点C到边的距离.
41.(2024八下·合肥期中) 如图,在矩形ABCD中,AB=6cm,BC=12cm,点P从点A沿边AB向点B以1cm/s的速度移动;同时,点Q从点B沿边BC向点C以2cm/s的速度移动.
(1)问几秒后△PBQ的面积等于8cm2?
(2)是否存在这样的时刻,使=8cm2,试说明理由.
42.(2024八下·合肥期中)已知,关于x的方程有两个实数根、.
(1)求实数m的取值范围;
(2)若、满足,求实数m的值.
43.(2024八下·涡阳期中)阅读教材P13的海伦—秦九韶公式,设一个三角形的三边长分别为a,b,c,则有下列三角形面积公式:①海伦公式:,;②秦九韶公式:(其中).请根据上述公式,解答下列问题:
(1)若一个三角形的三边长分别为5,6,7,求该三角形的面积;(利用海伦公式求解)
(2)若一个三角形的三边长分别为,,,求该三角形的面积.(利用秦九韶公式求解)
44.(2024八下·桐城期中)如图,在中,,,,点从点出发,沿着射线以的速度运动,运动时间为.
(1)若,则的值为______;
(2)当时,求的值;
(3)当是直角三角形时,求的值.
45.(2024八下·六安期中) 冬季来临,某超市以每件35元的价格购进某款棉帽,并以每件58的价格出售. 经统计,10月份的销售量为256只,12月份的销售量为400只.
(1)求该款棉帽10月份到12月份销售量的月平均增长率;
(2)经市场预测,下个月份的销售量将与12月份持平,现超市为了减少库存,采用降价促销方式,调查发现,该棉帽每降价1元,月销售量就会增加20只. 当该棉帽售价为多少元时,月销售利润达8400元?
46.(2024八下·六安期中) 关于x的方程.
(1)求证:方程恒有两个不相等的实数根;
(2)若此方程的一个根为1,求m的值.
47.(2024八下·太和期中)若两个二次根式m,n满足; ,且q是有理数,则称m与n是关于q的“共轭二次根式”.
(1)若m与 是关于的“共轭二次根式”,求m的值.
(2)若与 是关于的“共轭二次根式”,求a的值.
48.(2024八下·合肥期中)图中的螺旋形由一系列直角三角形组成,是直角边为1的直角三角形,以的斜边为直角边,长为1的线段为另一直角边,画第二个直角三角形……依此类推.
(1)第一个直角三角形的斜边长为______.
(2)第n个直角三角形的斜边长为______.
(3)求的值.
答案解析部分
1.(1)米;
(2)米.
2.(1)
(2)
3.(1)
(2)
(3)或或.
4.的长为或.
5.(1)
(2)0
6.(1),
(2)4
(3)或或
7.(1)
(2)当时,有一个实数根;当且时,有两个不相等的实数根.
8.(1);(2)6
9.11人
10.(1);
(2).
11.解:设水深x尺,芦苇(x+1)尺,
由勾股定理:x2+52=(x+1)2,
解得:x=12,x+1=13,
答:水深12尺,芦苇的长度是13尺.
找到题中的直角三角形,设水深为x尺,根据勾股定理解答.
12.(1)6,
(2)
13.(1)5,81.5;(2)90°(3)九年级一共有180名学生的体质达标
14.(1)、
(2)
(3)190(户)
15.解:如图所示
设旗杆高度为 ,则 , , ,
在 中,
解得: ,
答:旗杆的高度为 m.
结合题意,利用勾股定理计算求解即可。
16.
17.(1)温室花房的面积为,小路的面积为
(2)道路的宽度为
18.
19..
20.(1)13;(2)
21.(1),,
为的平分线,,
,
,四边形是平行四边形,
,平行四边形是菱形.
(2)四边形是菱形,,,
,,,,
在中,,.
(3)如图,在(2)的条件下,
,.
,,
或.
22.
23.(1)A、C两点之间的距离为15cm;
(2)114(cm2)
24.32°;垂直平分(是的垂直平分线)
25.(1);(2)
26.(1)当时,四边形是正方形;
(2)当时;
(3)
27.周长为;高为
28.(1)
(2)
(3)
29.(1)是等腰三角形,理由如下:
如图,取的中点,连接,,
分别是,的中点,
,分别是,的中位线,
,,
,,,
,
,
是等腰三角形.
(2)如图,连接,取的中点,连接,,
分别是,的中点,
,分别是的中位线,
,
,
,
.
30.(1)证明:四边形是平行四边形,,,
,分别为边,的中点,
,,,
四边形是平行四边形.
(2)解:四边形是矩形,理由如下:
如图,延长,交于点,
平分,
,
,
,
四边形是矩形.
31.解:
设,则,
由勾股定理得:,,,解得:,,
.
32.(1)
(2)
(3)2
33.(1)解:由题意得:,
∴
解得:,
∴的值为或
(2)解:由题意得:
∴
即:
解得:,
当时,
∴舍去
当时,
∴的值为10.
(1)根据题意可知方程有两个相等的实数根,利用判别式可得关于m的一元二次方程,解方程即可得到答案;
(2)根据题意可知方程的两实数根之积等于 ,利用根与系数的关系得到,即可得到关于m的一元二次方程,解方程即可求出m的值,进而即可得到答案.
34.(1)5
(2)2;
(3)
35.(1)解:由折叠的性质可知,
∴,
∵四边形是矩形,
∴,
∵,
∴,
∴线段的长度是;
(2)解:由(1)可知,
∴,
设,则,
∴,
∴,
解得:,
∴线段的长度是,
∴线段的长度是.
(1)由折叠的性质可知,即,根据矩形的性质得到,再利用勾股定理即可求出线段的长度;
(2)由(1)求出,设,则,即,根据勾股定理建立关于x的方程,解方程求得,即线段的长度是,进而即可求出线段的长度.
36.解:设AE=x,则BE=25﹣x,
由勾股定理得:
在Rt△ADE中,
DE2=AD2+AE2=102+x2,
在Rt△BCE中,
CE2=BC2+BE2=152+(25﹣x)2,
由题意可知:DE=CE,
所以:102+x2=152+(25﹣x)2,
解得:x=15km.(6分)
所以,E应建在距A点15km处
根据题意设出E点坐标,再由勾股定理列出方程求解即可.
37.(1)且
(2)
38.(1)3
(2)
39.(1)解:∵,,
∴,
∴“勾系一元二次方程”为:;
(2)证明:根据题意,得,
∵,
∴,
∴,
∴“勾系一元二次方程”必有实数根;
(3)解:当时,有,即,
∵四边形的周长是,
∴,即,
∴,
∴,
∴,,
∵,
∴
∴,
∴.
⑴、根据勾股定理先求得斜边c的值,然后将a、b、c的值代入“勾系一元二次方程 ”即可写出该勾系一元二次方程。
⑵、证明一元二次方程有实数根,也即证明该方程的根的判别式大于或等于零即可。
⑶、把方程的根代入一元二次方程可得a、b、c间的一个数量关系;根据四边形周长又可得a、b、c间的另一个数量关系;根据上述两关系式,可求得c的值,再加上a、b、c满足勾股定理,进一步得到abd的值,进而求出三角形ABC的面积。
40.(1)解:不是直角三角形,理由如下∶
根据勾股定理知,,,,
,
∴不是直角三角形;
(2)解:
(3)解:设点C到的距离是h.
由(2)知,三角形的面积是,
则,即,
解得,
点C到的距离为;
⑴、把三斜线段利用网格组成直角三角形,利用勾股定理可求其线段长,然后根据勾股定理逆定理判断三角形ABC是否是直角三角形。
⑵、利用割补法将三角形ABC的面积转化为边长为3 的正方形减去周围三个直角三角形面积即可。
41.(1)解:设x秒后△PBQ的面积等于8cm2.
则AP=x,QB=2x,∴PB=6﹣x,∴×(6﹣x)2x=8,解得,.
答:2秒或4秒后△PBQ的面积等于8cm2;
(2)解:设出发x秒时△DPQ的面积等于8cm2.∵S矩形ABCD﹣S△APD﹣S△BPQ﹣S△CDQ=S△DPQ,∴12×6﹣×12x﹣×2x(6﹣x)﹣×6×(12﹣2x)=8,化简整理得:,∵△=36﹣4×28=﹣76<0,∴原方程无解,∴不存在这样的时刻,使S△PDQ=8cm2.
(1)设x秒后△PBQ的面积等于8cm2,则AP=x,QB=2x,得到PB=6﹣x,根据△PBQ的面积等于8cm2列出方程,解方程即可得到答案;
(2)设出发x秒时△DPQ面积等于8cm2,根据题意得到,利用三角形面积公式得到关于x的一元二次方程,解方程即可得到答案.
42.(1)
(2)
43.(1)
(2)
44.(1)2或14
(2)
(3)8或
45.(1)解:设该款棉帽10月份到12月份销售量的月平均增长率为x,
根据题意得:,
解得:,(不符合题意,舍去)
答:该款棉帽10月份到12月份销售量的月平均增长率为.
(2)解:设该棉帽售价为y元,则每件的销售利润为元,月销售量为
件
根据题意得:
解得:(不符合题意,舍去).
答:该款棉帽售价为元时,月销售利润达8400元.
(1)设该款棉帽10月份到12月份销售量的月平均增长率为x,根据题意列出方程,解方程即可得到答案;
(2)设该棉帽售价为y元,则每件的销售利润为元,销售量为件,根据题意列出关于y的一元二次方程,解方程即可得到答案.
46.(1)证明:,
∵,
∴,
∵在实数范围内,m无论取何值,都有,即.
∴关于x的方程恒有两个不相等的实数根.
(2)解:将代入方程,
可得,
解得.
根据方程恒有两个不相等的实数根,即,得到,即在实数范围内,m无论取何值,都有,即,即可得到答案;
(2)将代入方程得到,求解即可得到答案.
47.(1)
(2)
48.(1)
(2)
(3)
期中真题专项复习04 解答题
一、解答题
1.(2024八下·濉溪期末)周末,小明和小亮去汉风公园放风筝,为了测得风筝的垂直高度,他们进行了如下操作:
测得水平距离的长为米;
根据手中剩余线的长度计算出风筝线的长为米;
牵线放风筝的小明的身高为米.
(1)求风筝的垂直高度;
(2)如果小明想风筝沿方向下降米,则他应该往回收线多少米?
2.(2024八下·霍邱期末)已知关于的一元二次方程有两个不同的实数根.
(1)求的取值范围;
(2)若方程的两个根的差为2,求的值.
3.(2024八下·庐江期末)已知,如图,在平面直角坐标系中,直线分别交x轴于点A,交y轴于点B,线段的垂直平分线分别交x轴于点C,交y轴于点D,交于点E.
(1)求点E的坐标;
(2)求直线的解析式;
(3)平面内是否存在点F,使得以B、C、D、F为顶点的四边形是平行四边形,若存在,直接写出点F的坐标.
4.(2024八下·庐江期末)已知中,,,边上的高,求边的长.
5.(2024八下·合肥月考)已知关于x的一元二次方程 有两个实数根,.
(1)求的取值范围;
(2)当时,求的值.
6.(2024八下·萧县期末)如图所示,在平面直角坐标系中,的边在x轴上,点D在y轴上.已知,,,从C点出发的E点,以每秒2个单位长度的速度向D点移动.M是的中点,的延长线交于F点.
(1)求点B,C的坐标.
(2)当四边形是平行四边形时,求点E的移动时间t.
(3)当为等腰三角形时,直接写出点E的坐标______.
7.(2024七下·全椒期末)已知关于x的方程无实数根.
(1)求m的取值范围;
(2)判断方程的根的情况.
8.(2024八下·合肥期末)已知关于x 的一元二次方程x2 -5x + m = 0.
(1)若方程有实数根,求实数m 的取值范围;
(2)若方程两实数根为x1,x2,且满足3 x1-2x2 =5,求实数m 的值.
9.(2024八下·界首期末)国庆节时,某班一个数学小组,为庆祝祖国华诞,他们每两人之间互送贺卡一张,已知全组共送贺卡110张, 问这个小组一共有多少人?
10.(2024八下·安庆期末)已知关于的一元二次方程有两个实数根.
(1)求实数的取值范围;
(2)若,求的值.
11.(2024八下·浏阳期中)我国古代数学著作《九章算术》中的一个问题.原文是:今有池方一丈,葭生其中央,出水尺.引葭赴岸,适与岸齐问水深、葭长各几何译文大意是:如图,有一个水池,水面是一个边长为10尺的正方形,在水池正中央有一根芦苇,它高出水面1尺.如果把这根芦苇拉向水池边的中点,它的顶端恰好到达池边的水面.问水的深度与这根芦苇的长度分别是多少?
12.(2024八下·利辛期末)如图,观察图形,认真分析,其中表示的面积,表示的面积,…,以此类推.
,;
,;
,;
….
根据以上规律,解答下列问题:
(1)填空:______,______;
(2)求的值.
13.(2024八下·芜湖期末)为加强中学生体育锻炼,学校组织了九年级300名学生进行了体质监测,现随机抽取了部分同学的成绩(百分制).制成如图不完整的统计图表:
表一
成绩x X<60 60≤x<70 70≤x<80 80≤x<90 90≤x<100
人数 1 2 a 8 4
表二
统计量 平均数 中位数 众数
成绩 79.7 b 72
根据以上信息回答下列问题:
(1)若抽取的学生成绩处在80≤x<90这一组的数据如下:
88 87 81 80 82 88 84 86
根据以上数据将表一和表二补充完整:a ;b ;
(2)在扇形统计图中,表示问卷成绩在70≤x<80这一组的扇形圆心角度数为 ;
(3)若成绩在80分及以上为体质达标,请你估计该校九年级一共有多少名学生的体质达标?
14.(2024八下·霍邱期末)甲,乙两个小区各有户居民,为了解两个小区3月份用户使用燃气量情况,小明和小丽分别从中随机抽取30户进行调查,并对数据进行整理、描述和分析.下面给出了部分信息.
a.甲小区用气量频数分布表如下:
分组
频数 3 6 10 3
b.乙小区用气量频数分布直方图如下(数据分成5组:,,,,)
c.乙小区用气量的数据在这一组的是:
d.甲,乙两小区用气量的平均数、中位数、众数如下:
小区 平均数 中位数 众数
甲
乙
根据以上信息,回答下列问题:
(1)写出表中m和n的值;
(2)在甲小区抽取的用户中,记3月份用气量高于他们的平均用气量的户数为.在乙小区抽取的用户中,记3月份用气量高于他们的平均用气量的户数为.比较,的大小,并说明理由;
(3)估计甲乙两小区中用气量不小于20立方米的总户数.
15.(2024八下·澧县期中)看着冉冉升起的五星红旗,你们是否想过旗杆到底有多高呢?某数学兴趣小组为了测量旗杆高度,进行以下操作:如图1,先将升旗的绳子拉到旗杆底端,发现绳子末端刚好接触到地面;如图2,再将绳子末端拉到距离旗杆8m处,发现绳子末端距离地面2m.请根据以上测量情况,计算旗杆的高度.
16.(2024八下·霍邱期末)如图,在四边形中,,,,,求的长.
17.(2024八下·庐阳期中)某公园准备在一块长为,宽为的长方形花园内修建一个底部为正方形的温室花房(如图所示),在温室花房四周修四条宽度相同,且与温室花房各边垂直的小路,温室花房边长是小路宽度的倍,花园内其他的空白地方铺草坪,设小路宽度为.
(1)用含的代数式分别表示花园内温室花房的面积和小路面积;
(2)若草坪面积为时,求这时道路宽度.
18.(2024八下·庐阳期中)若关于的方程有实数根,求的取值范围.
19.(2024八下·庐阳期中)解方程:3x2﹣2x﹣1=0.
20.(2024八下·涡阳期中)已知,
(1)求的值;
(2)若的小数部分为m,的小数部分为n,求的值.
21.(2024八下·庐江期中)如图,在四边形中,,,对角线,交于点,平分,过点作交的延长线于点,连接.
(1)求证:四边形是菱形;
(2)若,求的长;
(3)在(2)的条件下,已知点是线段上一点,且,求的长.
22.(2024八下·庐江月考)如图,四边形是平行四边形,点,分别为线段,的中点.若,求的度数.
23.(2024八下·池州月考)如图,有一张四边形纸片ABCD,AB⊥BC.经测得AB=9cm,BC=12cm,CD=8cm,AD=17cm.
(1)求A、C两点之间的距离.
(2)求这张纸片的面积.
24.(2024八下·池州月考)如图,在正方形中,点分别是边的中点,相交于点,连接.
(1)若,则的度数是 ;
(2)连接,则与之间的位置关系是 .
25.(2024八下·安徽期末)关于的一元二次方程有两个不相等的实数根、.
(1)求的取值范围;
(2)若,求的值.
26.(2024八下·天长月考)如图,在矩形中,,点P与点Q同时出发,点P从点D出发向点A运动,运动到点A停止,点Q从点B出发向点C运动,运动到点C停止,点P,Q的速度都是,连接,设点P,Q的运动时间为.
(1)求当t为何值时,四边形是正方形;
(2)求当t为何值时,;
(3)当四边形的面积为时,求矩形的周长与四边形的周长的比值.
27.(2024八下·天长月考)如图,在边长为1个单位长度的小正方形组成的网格中,的顶点都在小正方形网格线的交点上.求的周长及边上的高.
28.(2024八下·合肥期末)观察下列等式:
第1个等式:;
第2个等式:;
第3个等式:,
……
按照以上规律,解决下列问题.
(1)写出第4个等式:______.
(2)写出你猜想的第n个等式(用含n的等式表示).
(3)请用(2)中发现的规律计算:.
29.(2024八下·庐江期中)
(1)如图1,在四边形中,与相交于点,,,分别是,的中点,连接,分别交,于点,,判断的形状,并说明理由;
(2)如图2,在四边形中,,,分别是,的中点,连接并延长,分别与,的延长线交于点,.求证:.
30.(2024八下·庐江期中)如图,在平行四边形ABCD中,E,F分别为边AB,CD的中点,BD是对角线.
(1)求证:四边形DEBF是平行四边形;
(2)当DE平分∠ADB时,判断四边形DEBF是什么特殊的平行四边形,并说明理由.
31.(2024八下·庐江期中)在中,,,,求的面积.
某学习小组经过合作交流,给出了下面的解题思路,请你按照他们的解题思路完成解答过程.作于,设,用含的式子表示根据勾股定理,利用作为“桥梁”,建立方程模型求出利用勾股定理求出的长,再计算三角形的面积.
32.(2024九上·无锡月考)如图,由两个全等的和构成的四边形,已知直角三角形的直角边长分别为m、n,斜边长为q,分别以m,,n为二次项系数、一次项系数和常数项构造的一元二次方程,称为勾股方程.
(1)直接写出一个勾股方程;
(2)若勾股方程有两个相等的实数根,求的值;
(3)若是勾股方程的一个根,且四边形的周长是6,求四边形的面积.
33.(2024八下·合肥期中) 已知关于的一元二次方程.
(1)若方程有两个相等的实数根,求的值;
(2)若方程的两实数根之积等于,求的值.
34.(2024八下·蜀山期中)请阅读下面的过程,完成相应的题目:
的整数部分是1,故的小数部分是.
(1)的整数部分是______;
(2)设分别是的整数部分和小数部分,则______,______;
(3)在(2)的条件下,若已知,为有理数,且,求的值.
35.(2024八下·六安期中) 如图,将,的长方形,沿过顶点A的直线为折痕折叠,使顶点B落在边上的点Q处.
(1)求的长;
(2)求的长.
36.(2024八下·岳麓月考)如图,在笔直的铁路上A、B两点相距25km,C、D为两村庄,DA=10km,CB=15km,DA⊥AB于A,CB⊥AB于B,现要在AB上建一个中转站E,使得C、D两村到E站的距离相等.求E应建在距A多远处?
37.(2024八下·利辛期中)若是关于的一元二次方程的两个实数根.
(1)求的取值范围;
(2)若,求的值.
38.(2024八下·利辛期中)如图,把长方形沿对折后点落在边的点处,,,求:
(1)的长;
(2)的长.
39.(2024八下·潜山期中) 如图,四边形是证明勾股定理时用到的一个图形,a,b,c是和边长,易知,这时我们把关于x的形如的一元二次方程称为“勾系一元二次方程”.
请解决下列问题:
(1)当,时,写出该“勾系一元二次方程”;
(2)求证:关于x的“勾系一元二次方程”必有实数根;
(3)如图,若是“勾系一元二次方程”的一个根,且四边形的周长是,求的面积.
40.(2024八下·潜山期中) 如图,方格中小正方形的边长为1,的三个顶点都在小正方形的格点上,求∶
(1)请判断三角形是否是直角三角形,并说明理由;
(2) 的面积;
(3)点C到边的距离.
41.(2024八下·合肥期中) 如图,在矩形ABCD中,AB=6cm,BC=12cm,点P从点A沿边AB向点B以1cm/s的速度移动;同时,点Q从点B沿边BC向点C以2cm/s的速度移动.
(1)问几秒后△PBQ的面积等于8cm2?
(2)是否存在这样的时刻,使=8cm2,试说明理由.
42.(2024八下·合肥期中)已知,关于x的方程有两个实数根、.
(1)求实数m的取值范围;
(2)若、满足,求实数m的值.
43.(2024八下·涡阳期中)阅读教材P13的海伦—秦九韶公式,设一个三角形的三边长分别为a,b,c,则有下列三角形面积公式:①海伦公式:,;②秦九韶公式:(其中).请根据上述公式,解答下列问题:
(1)若一个三角形的三边长分别为5,6,7,求该三角形的面积;(利用海伦公式求解)
(2)若一个三角形的三边长分别为,,,求该三角形的面积.(利用秦九韶公式求解)
44.(2024八下·桐城期中)如图,在中,,,,点从点出发,沿着射线以的速度运动,运动时间为.
(1)若,则的值为______;
(2)当时,求的值;
(3)当是直角三角形时,求的值.
45.(2024八下·六安期中) 冬季来临,某超市以每件35元的价格购进某款棉帽,并以每件58的价格出售. 经统计,10月份的销售量为256只,12月份的销售量为400只.
(1)求该款棉帽10月份到12月份销售量的月平均增长率;
(2)经市场预测,下个月份的销售量将与12月份持平,现超市为了减少库存,采用降价促销方式,调查发现,该棉帽每降价1元,月销售量就会增加20只. 当该棉帽售价为多少元时,月销售利润达8400元?
46.(2024八下·六安期中) 关于x的方程.
(1)求证:方程恒有两个不相等的实数根;
(2)若此方程的一个根为1,求m的值.
47.(2024八下·太和期中)若两个二次根式m,n满足; ,且q是有理数,则称m与n是关于q的“共轭二次根式”.
(1)若m与 是关于的“共轭二次根式”,求m的值.
(2)若与 是关于的“共轭二次根式”,求a的值.
48.(2024八下·合肥期中)图中的螺旋形由一系列直角三角形组成,是直角边为1的直角三角形,以的斜边为直角边,长为1的线段为另一直角边,画第二个直角三角形……依此类推.
(1)第一个直角三角形的斜边长为______.
(2)第n个直角三角形的斜边长为______.
(3)求的值.
答案解析部分
1.(1)米;
(2)米.
2.(1)
(2)
3.(1)
(2)
(3)或或.
4.的长为或.
5.(1)
(2)0
6.(1),
(2)4
(3)或或
7.(1)
(2)当时,有一个实数根;当且时,有两个不相等的实数根.
8.(1);(2)6
9.11人
10.(1);
(2).
11.解:设水深x尺,芦苇(x+1)尺,
由勾股定理:x2+52=(x+1)2,
解得:x=12,x+1=13,
答:水深12尺,芦苇的长度是13尺.
找到题中的直角三角形,设水深为x尺,根据勾股定理解答.
12.(1)6,
(2)
13.(1)5,81.5;(2)90°(3)九年级一共有180名学生的体质达标
14.(1)、
(2)
(3)190(户)
15.解:如图所示
设旗杆高度为 ,则 , , ,
在 中,
解得: ,
答:旗杆的高度为 m.
结合题意,利用勾股定理计算求解即可。
16.
17.(1)温室花房的面积为,小路的面积为
(2)道路的宽度为
18.
19..
20.(1)13;(2)
21.(1),,
为的平分线,,
,
,四边形是平行四边形,
,平行四边形是菱形.
(2)四边形是菱形,,,
,,,,
在中,,.
(3)如图,在(2)的条件下,
,.
,,
或.
22.
23.(1)A、C两点之间的距离为15cm;
(2)114(cm2)
24.32°;垂直平分(是的垂直平分线)
25.(1);(2)
26.(1)当时,四边形是正方形;
(2)当时;
(3)
27.周长为;高为
28.(1)
(2)
(3)
29.(1)是等腰三角形,理由如下:
如图,取的中点,连接,,
分别是,的中点,
,分别是,的中位线,
,,
,,,
,
,
是等腰三角形.
(2)如图,连接,取的中点,连接,,
分别是,的中点,
,分别是的中位线,
,
,
,
.
30.(1)证明:四边形是平行四边形,,,
,分别为边,的中点,
,,,
四边形是平行四边形.
(2)解:四边形是矩形,理由如下:
如图,延长,交于点,
平分,
,
,
,
四边形是矩形.
31.解:
设,则,
由勾股定理得:,,,解得:,,
.
32.(1)
(2)
(3)2
33.(1)解:由题意得:,
∴
解得:,
∴的值为或
(2)解:由题意得:
∴
即:
解得:,
当时,
∴舍去
当时,
∴的值为10.
(1)根据题意可知方程有两个相等的实数根,利用判别式可得关于m的一元二次方程,解方程即可得到答案;
(2)根据题意可知方程的两实数根之积等于 ,利用根与系数的关系得到,即可得到关于m的一元二次方程,解方程即可求出m的值,进而即可得到答案.
34.(1)5
(2)2;
(3)
35.(1)解:由折叠的性质可知,
∴,
∵四边形是矩形,
∴,
∵,
∴,
∴线段的长度是;
(2)解:由(1)可知,
∴,
设,则,
∴,
∴,
解得:,
∴线段的长度是,
∴线段的长度是.
(1)由折叠的性质可知,即,根据矩形的性质得到,再利用勾股定理即可求出线段的长度;
(2)由(1)求出,设,则,即,根据勾股定理建立关于x的方程,解方程求得,即线段的长度是,进而即可求出线段的长度.
36.解:设AE=x,则BE=25﹣x,
由勾股定理得:
在Rt△ADE中,
DE2=AD2+AE2=102+x2,
在Rt△BCE中,
CE2=BC2+BE2=152+(25﹣x)2,
由题意可知:DE=CE,
所以:102+x2=152+(25﹣x)2,
解得:x=15km.(6分)
所以,E应建在距A点15km处
根据题意设出E点坐标,再由勾股定理列出方程求解即可.
37.(1)且
(2)
38.(1)3
(2)
39.(1)解:∵,,
∴,
∴“勾系一元二次方程”为:;
(2)证明:根据题意,得,
∵,
∴,
∴,
∴“勾系一元二次方程”必有实数根;
(3)解:当时,有,即,
∵四边形的周长是,
∴,即,
∴,
∴,
∴,,
∵,
∴
∴,
∴.
⑴、根据勾股定理先求得斜边c的值,然后将a、b、c的值代入“勾系一元二次方程 ”即可写出该勾系一元二次方程。
⑵、证明一元二次方程有实数根,也即证明该方程的根的判别式大于或等于零即可。
⑶、把方程的根代入一元二次方程可得a、b、c间的一个数量关系;根据四边形周长又可得a、b、c间的另一个数量关系;根据上述两关系式,可求得c的值,再加上a、b、c满足勾股定理,进一步得到abd的值,进而求出三角形ABC的面积。
40.(1)解:不是直角三角形,理由如下∶
根据勾股定理知,,,,
,
∴不是直角三角形;
(2)解:
(3)解:设点C到的距离是h.
由(2)知,三角形的面积是,
则,即,
解得,
点C到的距离为;
⑴、把三斜线段利用网格组成直角三角形,利用勾股定理可求其线段长,然后根据勾股定理逆定理判断三角形ABC是否是直角三角形。
⑵、利用割补法将三角形ABC的面积转化为边长为3 的正方形减去周围三个直角三角形面积即可。
41.(1)解:设x秒后△PBQ的面积等于8cm2.
则AP=x,QB=2x,∴PB=6﹣x,∴×(6﹣x)2x=8,解得,.
答:2秒或4秒后△PBQ的面积等于8cm2;
(2)解:设出发x秒时△DPQ的面积等于8cm2.∵S矩形ABCD﹣S△APD﹣S△BPQ﹣S△CDQ=S△DPQ,∴12×6﹣×12x﹣×2x(6﹣x)﹣×6×(12﹣2x)=8,化简整理得:,∵△=36﹣4×28=﹣76<0,∴原方程无解,∴不存在这样的时刻,使S△PDQ=8cm2.
(1)设x秒后△PBQ的面积等于8cm2,则AP=x,QB=2x,得到PB=6﹣x,根据△PBQ的面积等于8cm2列出方程,解方程即可得到答案;
(2)设出发x秒时△DPQ面积等于8cm2,根据题意得到,利用三角形面积公式得到关于x的一元二次方程,解方程即可得到答案.
42.(1)
(2)
43.(1)
(2)
44.(1)2或14
(2)
(3)8或
45.(1)解:设该款棉帽10月份到12月份销售量的月平均增长率为x,
根据题意得:,
解得:,(不符合题意,舍去)
答:该款棉帽10月份到12月份销售量的月平均增长率为.
(2)解:设该棉帽售价为y元,则每件的销售利润为元,月销售量为
件
根据题意得:
解得:(不符合题意,舍去).
答:该款棉帽售价为元时,月销售利润达8400元.
(1)设该款棉帽10月份到12月份销售量的月平均增长率为x,根据题意列出方程,解方程即可得到答案;
(2)设该棉帽售价为y元,则每件的销售利润为元,销售量为件,根据题意列出关于y的一元二次方程,解方程即可得到答案.
46.(1)证明:,
∵,
∴,
∵在实数范围内,m无论取何值,都有,即.
∴关于x的方程恒有两个不相等的实数根.
(2)解:将代入方程,
可得,
解得.
根据方程恒有两个不相等的实数根,即,得到,即在实数范围内,m无论取何值,都有,即,即可得到答案;
(2)将代入方程得到,求解即可得到答案.
47.(1)
(2)
48.(1)
(2)
(3)
同课章节目录
