期中真题专项复习02填空题(含答案)--2024-2025学年八年级数学下册(沪科版2024)
文档属性
| 名称 | 期中真题专项复习02填空题(含答案)--2024-2025学年八年级数学下册(沪科版2024) |  | |
| 格式 | docx | ||
| 文件大小 | 449.2KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-03-30 06:09:46 | ||
图片预览

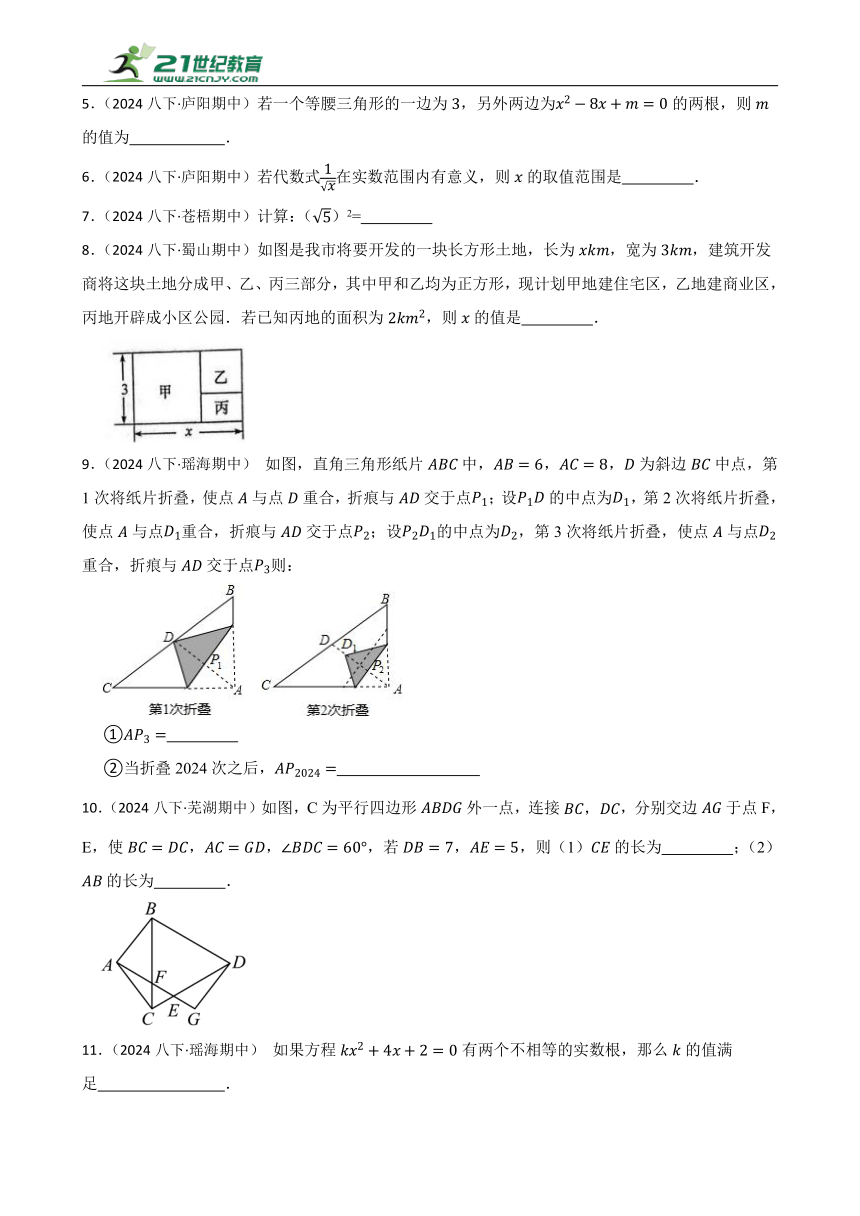

文档简介
2024-2025学年八年级数学下册(沪科版2024)
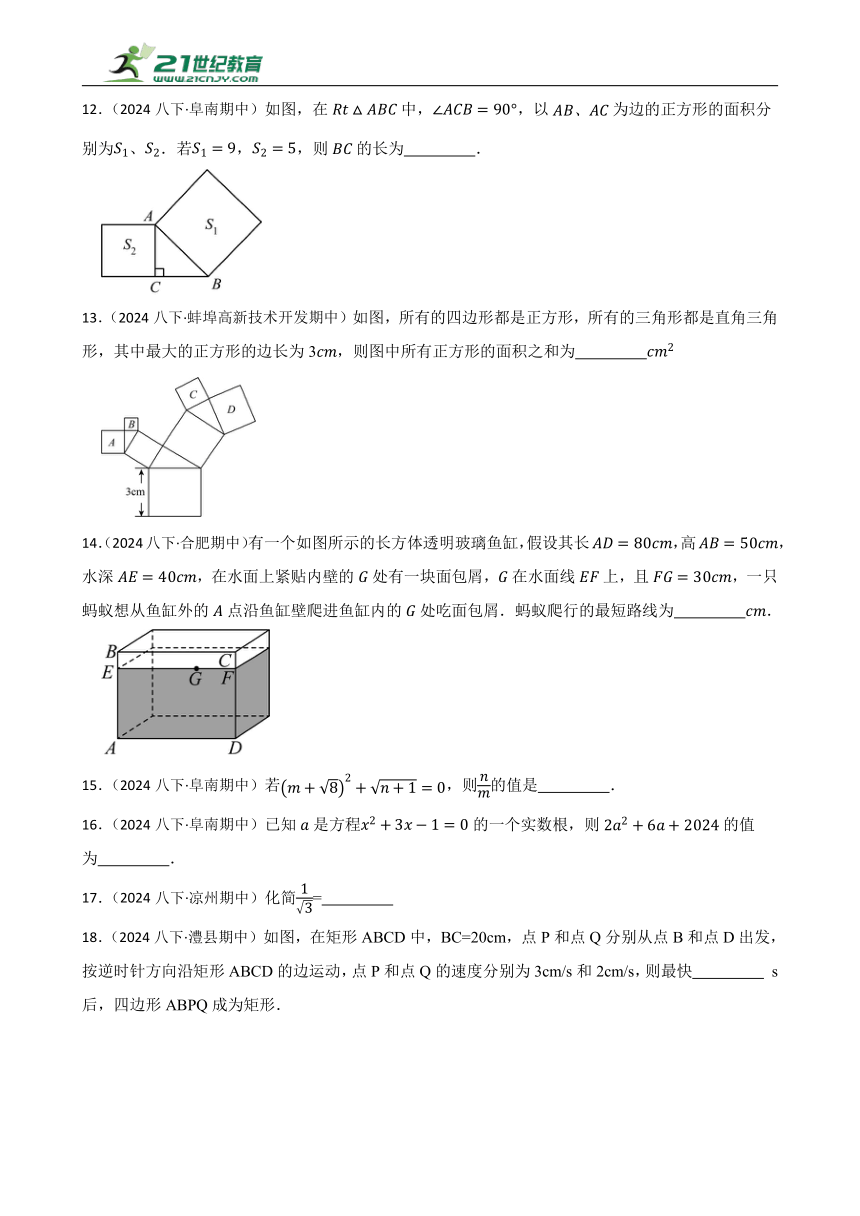
期中真题专项复习02填空题
一、填空题
1.(2023八下·大竹期中)如图,在正方形ABCD中,边长为2的等边三角形AEF的顶点E、F分别在BC和CD上,下列结论:①CE=CF;②∠AEB=75°;③BE+DF=EF;④S正方形ABCD=.
其中正确的序号是 (把你认为正确的都填上).
2.(2024八下·庐阳期中)如图所示,点和点分别为轴与轴上一点,且,为直线上一点,作交轴于点.
()若点的横坐标为,则 ;
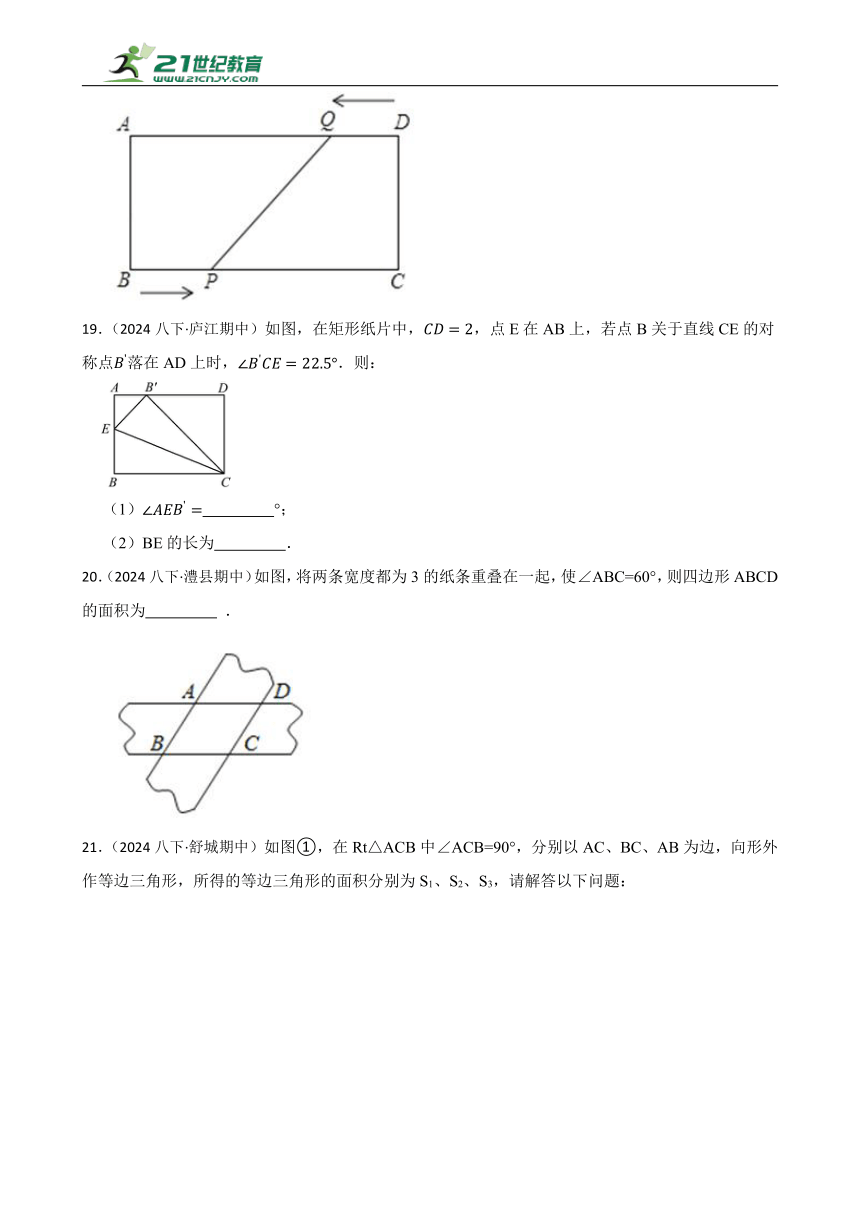
()若为线段中点,连接,则的最小值为 .
3.(2024八下·大观期中) 定义:若、是方程的两个整数根,且满足,则称此类方程为“自然方程”,例如:是“自然方程”.
⑴下列方程是“自然方程”的是 ;(填序号)
①;②;③.
⑵若方程是“自然方程”,m的值为 .
4.(2024八下·庐阳期中)如图,已知中,,,,是的中点,连接,则的值为 .
5.(2024八下·庐阳期中)若一个等腰三角形的一边为,另外两边为的两根,则的值为 .
6.(2024八下·庐阳期中)若代数式在实数范围内有意义,则的取值范围是 .
7.(2024八下·苍梧期中)计算:()2=
8.(2024八下·蜀山期中)如图是我市将要开发的一块长方形土地,长为,宽为,建筑开发商将这块土地分成甲、乙、丙三部分,其中甲和乙均为正方形,现计划甲地建住宅区,乙地建商业区,丙地开辟成小区公园.若已知丙地的面积为,则的值是 .
9.(2024八下·瑶海期中) 如图,直角三角形纸片中,,,为斜边中点,第1次将纸片折叠,使点与点重合,折痕与交于点;设的中点为,第2次将纸片折叠,使点与点重合,折痕与交于点;设的中点为,第3次将纸片折叠,使点与点重合,折痕与交于点则:
①
②当折叠2024次之后,
10.(2024八下·芜湖期中)如图,C为平行四边形外一点,连接,分别交边于点F,E,使,,,若,,则(1)的长为 ;(2)的长为 .
11.(2024八下·瑶海期中) 如果方程有两个不相等的实数根,那么的值满足 .
12.(2024八下·阜南期中)如图,在中,,以为边的正方形的面积分别为、.若,,则的长为 .
13.(2024八下·蚌埠高新技术开发期中)如图,所有的四边形都是正方形,所有的三角形都是直角三角形,其中最大的正方形的边长为3,则图中所有正方形的面积之和为
14.(2024八下·合肥期中)有一个如图所示的长方体透明玻璃鱼缸,假设其长,高,水深,在水面上紧贴内壁的处有一块面包屑,在水面线上,且,一只蚂蚁想从鱼缸外的点沿鱼缸壁爬进鱼缸内的处吃面包屑.蚂蚁爬行的最短路线为 .
15.(2024八下·阜南期中)若,则的值是 .
16.(2024八下·阜南期中)已知是方程的一个实数根,则的值为 .
17.(2024八下·凉州期中)化简=
18.(2024八下·澧县期中)如图,在矩形ABCD中,BC=20cm,点P和点Q分别从点B和点D出发,按逆时针方向沿矩形ABCD的边运动,点P和点Q的速度分别为3cm/s和2cm/s,则最快 s后,四边形ABPQ成为矩形.
19.(2024八下·庐江期中)如图,在矩形纸片中,,点E在AB上,若点B关于直线CE的对称点落在AD上时,.则:
(1) °;
(2)BE的长为 .
20.(2024八下·澧县期中)如图,将两条宽度都为3的纸条重叠在一起,使∠ABC=60°,则四边形ABCD的面积为 .
21.(2024八下·舒城期中)如图①,在Rt△ACB中∠ACB=90°,分别以AC、BC、AB为边,向形外作等边三角形,所得的等边三角形的面积分别为S1、S2、S3,请解答以下问题:
(1)S1、S2、S3满足的数量关系是 .
(2)现将△ABF向上翻折,如图②,若阴影部分的S甲=6、S乙=5、S丙=4,则= .
22.(2024八下·芜湖期中)我国南宋著名的数学家秦九韶,曾提出利用三角形的三边求面积的“秦九韶公式”(三斜求积术)∶ 若 一 个 三 角 形 的 三 边 长 分 别 为 a, b, c, 则 这 个 三 角 形 的 面 积.若一个三角形的三边长,,分别为,则这个三角形的面积为
23.(2024八下·武威期中)若直角三角形的一个锐角是,斜边长为1,则此直角三角形周长是 .
24.(2024八下·南谯期中)若a是方程的根,则的值为 .
25.(2024八下·开州期中)如图所示,在中,M是的中点,平分于N点,且,则 .
26.(2024八下·金安期中) 计算 .
27.(2024八下·阜阳期中)如图,的对角线,交于点, 是的中点,连结,,,若,则的长为 .
28.(2024八下·无为期中)如图,在正方形中,点分别在边上,是等边三角形.
(1)的度数是.
(2)连接交于点G,若,则线段的长度是.
29.(2024八下·无为期中)如图,在菱形中,O是对角线,的交点,E是边的中点,若,,则.
30.(2023八下·谷城期中)化简 ; .
31.(2024八下·蚌埠高新技术开发期中)如图,中,,,P是BC上的动点,Q是AC上的动点(Q不与A、C重合),
(1)线段PA的最小值为 ;
(2)当为直角三角形时,也为直角三角形时,则CQ的长度为 .
32.(2024八下·合肥期中) 已知实数且分别满足方程和方程,则代数式的值为 .
33.(2024八下·马鞍山期中)如图,点是等边内一点,连接、、,,以为边作,连接,则有以下结论:①是等边三角形;②是直角三角形;③;④,其中一定正确的是 .(把所有正确答案的序号都填在横线上)
34.(2024八下·马鞍山期中)一元二次方程的两根为,,则 .
35.(2024八下·蜀山期中)已知满足等式,则 .
36.(2024八下·马鞍山期中)一元二次方程的解是 .
37.(2024八下·桐城期中)如图,在中,,,已知.
(1)的长为 .
(2)点,分别是,上一点,沿着直线将折叠,得到,已知点落在边上,若是直角三角形,则的长为 (注:)
38.(2024八下·桐城期中)如图,在数轴上,点和点对应的实数分别是和,,,以点为旋转中心,以为半径画弧交数轴于点,则点表示的实数为 .
39.(2024八下·潜山期中)已知a,b是一元二次方程的两个根,则 .
40.(2024八下·六安期中) 如图,在中,,,D、E为上两点,,F为外一点,且,,则下列结论:①;②;③;④,其中正确的是 .
41.(2024八下·六安期中) 直角三角形的两条直角边长分别是6和8,则斜边上的高为 .
42.(2024八下·六安期中) 若最简二次根式与能合并成一项,则 .
43.(2024八下·太和期中)如图.在矩形中,E,F,G,H 为矩形四边的中点,依次连接点 E,F,G,H.
(1)四边形 的形状是 .
(2)若,则四边形的周长是 .
44.(2024八下·太和期中)如图,在中,,则的长为 .
45.(2024八下·庐江期中)如图,阴影部分是两个正方形,其他三个图形是一个正方形和两个直角三角形,则阴影部分的面积之和为 .
46.(2024八下·南谯期中)为贯彻《关于全面加强新时代大中小学劳动教育的意见》的方针政策,帮助同学们更好地理解劳动的价值与意义,培养学生的劳动情感、劳动能力和劳动品质,学校给八(1)班、八(2)班各分一块三角形形状的劳动试验基地.
(1)若班主任测量出八(1)班试验基地的三边长分别为,,,则这块试验基地的面积为
(2)八(2)班的劳动试验基地的三边长分别为,,(如图),则的面积为 .
47.(2024八下·合肥期中) 如果关于x的一元二次方程的一个解是,那么代数式的值是 .
48.(2024八下·蜀山期中)如图是我市将要开发的一块长方形的土地,长为,宽为,建筑开发商将这块土地分为甲、乙、丙三部分,其中甲和乙均为正方形,现计划甲地建住宅区,乙地建商业区,丙地开辟成小区公园,若已知丙地的面积为2km2,则x的值为 .
49.(2024八下·庐江期中)如图,为平行四边形的对角线,,于点,于点,,相交于点,直线交线段的延长线于点,下列结论:①;②;③;④.其中正确的结论有 .
50.(2024八下·合肥期中)如图,已知,则数轴上点B所表示的数是 .
答案解析部分
1.①②④
2.;
3.②;2或0
解:⑴①
,
∴,
∴,
则该方程的解不是整数,故此选项不符合题意;
②
∴,
∴,
∴,
∴,
∴该方程是“自然方程”;
③
∴,
∴,
则该方程的解不是整数,故此选项不符合题意;
故答案为:②
⑵,
∴,
∴,
∴,
∵方程是“自然方程”,
∴,
∴或0.
故答案为:2或0
⑴、根据“自然方程”的概念判定即可,通过求三个方程的解可知正确答案;
⑵、因为方程是“自然方程”,故有两整数解,且两解差的绝对值等于1,易得m的绝对值方程,根据绝对值的意义,转化为一元一次方程求解即可。
4.
5.或16
6.
7.5
解:()2=5.
故答案为:5.
直接利用二次根式的性质求出答案.
8.4或5
解:由题意得:丙的长为,丙的宽为,
∵丙地的面积为,列方程得:,即,
解得:,,
所以x的值为4或5 .
故答案为:4或5
根据题意列一元二次方程,解方程即可得解.
9.;
解:由勾股定理得:,
∵D是BC的中点,
∴,由折叠的性质得,
∵的中点为
∴,,,,
,,,
,
,
故,.
先写出,,,的长度,然后可发现规律推出的表达式,继而根据即可得出的表达式,也可得出的长.
10.2;
11.且
解:由题意得:且,
解得:且,
故答案为:且.
根据一元二次方程的定义和判别式的意义得到,,即可求解.
12.2
13.27
14.
15.
16.
17.
解:.
故答案为:.
直接利用二次根式的性质化简求出答案.
18.4
解;设最快x秒,四边形ABPQ成为矩形,由BP=AQ得
3x=20﹣2x.
解得x=4,
故答案为:4.
根据矩形的性质,可得BC与AD的关系,根据矩形的判定定理,可得BP=AQ,根据解题元一次方程,可得答案.
19.45;
20.6
解:∵纸条的对边平行,即AB∥CD,AD∥BC,
∴四边形ABCD是平行四边形,
∵两张纸条的宽度都是3,
∴S四边形ABCD=AB×3=BC×3,
∴AB=BC,
∴平行四边形ABCD是菱形,即四边形ABCD是菱形.
如图,过A作AE⊥BC,垂足为E,
∵∠ABC=60°,
∴∠BAE=90°﹣60°=30°,
∴AB=2BE,
在△ABE中,AB2=BE2+AE2,
即AB2=AB2+32,
解得AB=2,
∴S四边形ABCD=BC AE=2×3=6.
故答案是:6.
先根据两组对边分别平行证明四边形ABCD是平行四边形,再根据两张纸条的宽度相等,利用面积求出AB=BC,然后根据邻边相等的平行四边形是菱形;根据宽度是3cm与∠ABC=60°求出菱形的边长,然后利用菱形的面积=底×高计算即可.
21.S1+S2=S3;7
22.
23. 或 +
∵直角三角形的一个锐角是60°,斜边长为1,∴两个直角边的长分别为1×sin60°=32,1×cos60°=12,
∴此直角三角形周长是1+12+32=3+32.
本题考查特殊角的三角函数值,sin60°=32 , cos60°=12 .
24.2027
25.3
解:如图,延长BN交AC于点E,
∵AN平分∠BAE,∴∠BAN=∠EAN,
∵AN⊥BE,∴∠ANB=∠ANE=90°,
∵AN=AN,
∴△ANB≌△ANE(ASA),
∴BN=EN,AE=AB=10,
∵M是BC的中点,
∴MN为△BCE的中位线,
∴CE=2MN ,
∵CE=AC-AE=16-10=6,
∴MN=3;
故答案为:3.
延长BN交AC于点E,证明△ANB≌△ANE(ASA),可得BN=EN,AE=AB=10,可知MN为△BCE的中位线,可得CE=2MN ,由CE=AC-AE=6即可求出MN的长.
26.
,
故答案为:.
先利用完全平方公式及分母有理化化简,再计算即可.
27.
28.,
29.
30.;
31.3;3或4或4.5
32.
解:由题意得,将方程两边同时除以得,
∵,
∴,
∴a和为一元二次方程的两根,
∴,,
∴.
故答案为:.
将方程变形得到,得到a和为一元二次方程的两根,利用根与系数的关系得到,,代入代数式进行计算,即可得到答案.
33.①②③
34.
35.-1
解:,
,
,
解得:,
∴.
故答案为:.
根据二次根式非负性,偶次方的非负性求出,再代入,计算求解即可.
36.,
37.;或
38.
39.
40.①②④
41.4.8
解:∵两条直角边长分别是6和8,
∴斜边为,
设斜边上的高为h,
∴,
即h=4.8.
故答案为:4.8.
根据勾股定理求出斜边的长,根据面积相等,利用三角形的面积公式得到,即可求出斜边上的高.
42.3
43.菱形;
44.
45.64
46.;
47.
解:∵ 关于x的一元二次方程的一个解是,
∴a-b+1=0,
∴a-b=-1,
∴2024+a-b=2024-1=2023.
故答案为:2023.
根据题意可得a-b+1=0,变形得到a-b=-1,将其代入2024+a-b进行计算,即可得到答案.
48.4或5
49.②④
50.
期中真题专项复习02填空题
一、填空题
1.(2023八下·大竹期中)如图,在正方形ABCD中,边长为2的等边三角形AEF的顶点E、F分别在BC和CD上,下列结论:①CE=CF;②∠AEB=75°;③BE+DF=EF;④S正方形ABCD=.
其中正确的序号是 (把你认为正确的都填上).
2.(2024八下·庐阳期中)如图所示,点和点分别为轴与轴上一点,且,为直线上一点,作交轴于点.
()若点的横坐标为,则 ;
()若为线段中点,连接,则的最小值为 .
3.(2024八下·大观期中) 定义:若、是方程的两个整数根,且满足,则称此类方程为“自然方程”,例如:是“自然方程”.
⑴下列方程是“自然方程”的是 ;(填序号)
①;②;③.
⑵若方程是“自然方程”,m的值为 .
4.(2024八下·庐阳期中)如图,已知中,,,,是的中点,连接,则的值为 .
5.(2024八下·庐阳期中)若一个等腰三角形的一边为,另外两边为的两根,则的值为 .
6.(2024八下·庐阳期中)若代数式在实数范围内有意义,则的取值范围是 .
7.(2024八下·苍梧期中)计算:()2=
8.(2024八下·蜀山期中)如图是我市将要开发的一块长方形土地,长为,宽为,建筑开发商将这块土地分成甲、乙、丙三部分,其中甲和乙均为正方形,现计划甲地建住宅区,乙地建商业区,丙地开辟成小区公园.若已知丙地的面积为,则的值是 .
9.(2024八下·瑶海期中) 如图,直角三角形纸片中,,,为斜边中点,第1次将纸片折叠,使点与点重合,折痕与交于点;设的中点为,第2次将纸片折叠,使点与点重合,折痕与交于点;设的中点为,第3次将纸片折叠,使点与点重合,折痕与交于点则:
①
②当折叠2024次之后,
10.(2024八下·芜湖期中)如图,C为平行四边形外一点,连接,分别交边于点F,E,使,,,若,,则(1)的长为 ;(2)的长为 .
11.(2024八下·瑶海期中) 如果方程有两个不相等的实数根,那么的值满足 .
12.(2024八下·阜南期中)如图,在中,,以为边的正方形的面积分别为、.若,,则的长为 .
13.(2024八下·蚌埠高新技术开发期中)如图,所有的四边形都是正方形,所有的三角形都是直角三角形,其中最大的正方形的边长为3,则图中所有正方形的面积之和为
14.(2024八下·合肥期中)有一个如图所示的长方体透明玻璃鱼缸,假设其长,高,水深,在水面上紧贴内壁的处有一块面包屑,在水面线上,且,一只蚂蚁想从鱼缸外的点沿鱼缸壁爬进鱼缸内的处吃面包屑.蚂蚁爬行的最短路线为 .
15.(2024八下·阜南期中)若,则的值是 .
16.(2024八下·阜南期中)已知是方程的一个实数根,则的值为 .
17.(2024八下·凉州期中)化简=
18.(2024八下·澧县期中)如图,在矩形ABCD中,BC=20cm,点P和点Q分别从点B和点D出发,按逆时针方向沿矩形ABCD的边运动,点P和点Q的速度分别为3cm/s和2cm/s,则最快 s后,四边形ABPQ成为矩形.
19.(2024八下·庐江期中)如图,在矩形纸片中,,点E在AB上,若点B关于直线CE的对称点落在AD上时,.则:
(1) °;
(2)BE的长为 .
20.(2024八下·澧县期中)如图,将两条宽度都为3的纸条重叠在一起,使∠ABC=60°,则四边形ABCD的面积为 .
21.(2024八下·舒城期中)如图①,在Rt△ACB中∠ACB=90°,分别以AC、BC、AB为边,向形外作等边三角形,所得的等边三角形的面积分别为S1、S2、S3,请解答以下问题:
(1)S1、S2、S3满足的数量关系是 .
(2)现将△ABF向上翻折,如图②,若阴影部分的S甲=6、S乙=5、S丙=4,则= .
22.(2024八下·芜湖期中)我国南宋著名的数学家秦九韶,曾提出利用三角形的三边求面积的“秦九韶公式”(三斜求积术)∶ 若 一 个 三 角 形 的 三 边 长 分 别 为 a, b, c, 则 这 个 三 角 形 的 面 积.若一个三角形的三边长,,分别为,则这个三角形的面积为
23.(2024八下·武威期中)若直角三角形的一个锐角是,斜边长为1,则此直角三角形周长是 .
24.(2024八下·南谯期中)若a是方程的根,则的值为 .
25.(2024八下·开州期中)如图所示,在中,M是的中点,平分于N点,且,则 .
26.(2024八下·金安期中) 计算 .
27.(2024八下·阜阳期中)如图,的对角线,交于点, 是的中点,连结,,,若,则的长为 .
28.(2024八下·无为期中)如图,在正方形中,点分别在边上,是等边三角形.
(1)的度数是.
(2)连接交于点G,若,则线段的长度是.
29.(2024八下·无为期中)如图,在菱形中,O是对角线,的交点,E是边的中点,若,,则.
30.(2023八下·谷城期中)化简 ; .
31.(2024八下·蚌埠高新技术开发期中)如图,中,,,P是BC上的动点,Q是AC上的动点(Q不与A、C重合),
(1)线段PA的最小值为 ;
(2)当为直角三角形时,也为直角三角形时,则CQ的长度为 .
32.(2024八下·合肥期中) 已知实数且分别满足方程和方程,则代数式的值为 .
33.(2024八下·马鞍山期中)如图,点是等边内一点,连接、、,,以为边作,连接,则有以下结论:①是等边三角形;②是直角三角形;③;④,其中一定正确的是 .(把所有正确答案的序号都填在横线上)
34.(2024八下·马鞍山期中)一元二次方程的两根为,,则 .
35.(2024八下·蜀山期中)已知满足等式,则 .
36.(2024八下·马鞍山期中)一元二次方程的解是 .
37.(2024八下·桐城期中)如图,在中,,,已知.
(1)的长为 .
(2)点,分别是,上一点,沿着直线将折叠,得到,已知点落在边上,若是直角三角形,则的长为 (注:)
38.(2024八下·桐城期中)如图,在数轴上,点和点对应的实数分别是和,,,以点为旋转中心,以为半径画弧交数轴于点,则点表示的实数为 .
39.(2024八下·潜山期中)已知a,b是一元二次方程的两个根,则 .
40.(2024八下·六安期中) 如图,在中,,,D、E为上两点,,F为外一点,且,,则下列结论:①;②;③;④,其中正确的是 .
41.(2024八下·六安期中) 直角三角形的两条直角边长分别是6和8,则斜边上的高为 .
42.(2024八下·六安期中) 若最简二次根式与能合并成一项,则 .
43.(2024八下·太和期中)如图.在矩形中,E,F,G,H 为矩形四边的中点,依次连接点 E,F,G,H.
(1)四边形 的形状是 .
(2)若,则四边形的周长是 .
44.(2024八下·太和期中)如图,在中,,则的长为 .
45.(2024八下·庐江期中)如图,阴影部分是两个正方形,其他三个图形是一个正方形和两个直角三角形,则阴影部分的面积之和为 .
46.(2024八下·南谯期中)为贯彻《关于全面加强新时代大中小学劳动教育的意见》的方针政策,帮助同学们更好地理解劳动的价值与意义,培养学生的劳动情感、劳动能力和劳动品质,学校给八(1)班、八(2)班各分一块三角形形状的劳动试验基地.
(1)若班主任测量出八(1)班试验基地的三边长分别为,,,则这块试验基地的面积为
(2)八(2)班的劳动试验基地的三边长分别为,,(如图),则的面积为 .
47.(2024八下·合肥期中) 如果关于x的一元二次方程的一个解是,那么代数式的值是 .
48.(2024八下·蜀山期中)如图是我市将要开发的一块长方形的土地,长为,宽为,建筑开发商将这块土地分为甲、乙、丙三部分,其中甲和乙均为正方形,现计划甲地建住宅区,乙地建商业区,丙地开辟成小区公园,若已知丙地的面积为2km2,则x的值为 .
49.(2024八下·庐江期中)如图,为平行四边形的对角线,,于点,于点,,相交于点,直线交线段的延长线于点,下列结论:①;②;③;④.其中正确的结论有 .
50.(2024八下·合肥期中)如图,已知,则数轴上点B所表示的数是 .
答案解析部分
1.①②④
2.;
3.②;2或0
解:⑴①
,
∴,
∴,
则该方程的解不是整数,故此选项不符合题意;
②
∴,
∴,
∴,
∴,
∴该方程是“自然方程”;
③
∴,
∴,
则该方程的解不是整数,故此选项不符合题意;
故答案为:②
⑵,
∴,
∴,
∴,
∵方程是“自然方程”,
∴,
∴或0.
故答案为:2或0
⑴、根据“自然方程”的概念判定即可,通过求三个方程的解可知正确答案;
⑵、因为方程是“自然方程”,故有两整数解,且两解差的绝对值等于1,易得m的绝对值方程,根据绝对值的意义,转化为一元一次方程求解即可。
4.
5.或16
6.
7.5
解:()2=5.
故答案为:5.
直接利用二次根式的性质求出答案.
8.4或5
解:由题意得:丙的长为,丙的宽为,
∵丙地的面积为,列方程得:,即,
解得:,,
所以x的值为4或5 .
故答案为:4或5
根据题意列一元二次方程,解方程即可得解.
9.;
解:由勾股定理得:,
∵D是BC的中点,
∴,由折叠的性质得,
∵的中点为
∴,,,,
,,,
,
,
故,.
先写出,,,的长度,然后可发现规律推出的表达式,继而根据即可得出的表达式,也可得出的长.
10.2;
11.且
解:由题意得:且,
解得:且,
故答案为:且.
根据一元二次方程的定义和判别式的意义得到,,即可求解.
12.2
13.27
14.
15.
16.
17.
解:.
故答案为:.
直接利用二次根式的性质化简求出答案.
18.4
解;设最快x秒,四边形ABPQ成为矩形,由BP=AQ得
3x=20﹣2x.
解得x=4,
故答案为:4.
根据矩形的性质,可得BC与AD的关系,根据矩形的判定定理,可得BP=AQ,根据解题元一次方程,可得答案.
19.45;
20.6
解:∵纸条的对边平行,即AB∥CD,AD∥BC,
∴四边形ABCD是平行四边形,
∵两张纸条的宽度都是3,
∴S四边形ABCD=AB×3=BC×3,
∴AB=BC,
∴平行四边形ABCD是菱形,即四边形ABCD是菱形.
如图,过A作AE⊥BC,垂足为E,
∵∠ABC=60°,
∴∠BAE=90°﹣60°=30°,
∴AB=2BE,
在△ABE中,AB2=BE2+AE2,
即AB2=AB2+32,
解得AB=2,
∴S四边形ABCD=BC AE=2×3=6.
故答案是:6.
先根据两组对边分别平行证明四边形ABCD是平行四边形,再根据两张纸条的宽度相等,利用面积求出AB=BC,然后根据邻边相等的平行四边形是菱形;根据宽度是3cm与∠ABC=60°求出菱形的边长,然后利用菱形的面积=底×高计算即可.
21.S1+S2=S3;7
22.
23. 或 +
∵直角三角形的一个锐角是60°,斜边长为1,∴两个直角边的长分别为1×sin60°=32,1×cos60°=12,
∴此直角三角形周长是1+12+32=3+32.
本题考查特殊角的三角函数值,sin60°=32 , cos60°=12 .
24.2027
25.3
解:如图,延长BN交AC于点E,
∵AN平分∠BAE,∴∠BAN=∠EAN,
∵AN⊥BE,∴∠ANB=∠ANE=90°,
∵AN=AN,
∴△ANB≌△ANE(ASA),
∴BN=EN,AE=AB=10,
∵M是BC的中点,
∴MN为△BCE的中位线,
∴CE=2MN ,
∵CE=AC-AE=16-10=6,
∴MN=3;
故答案为:3.
延长BN交AC于点E,证明△ANB≌△ANE(ASA),可得BN=EN,AE=AB=10,可知MN为△BCE的中位线,可得CE=2MN ,由CE=AC-AE=6即可求出MN的长.
26.
,
故答案为:.
先利用完全平方公式及分母有理化化简,再计算即可.
27.
28.,
29.
30.;
31.3;3或4或4.5
32.
解:由题意得,将方程两边同时除以得,
∵,
∴,
∴a和为一元二次方程的两根,
∴,,
∴.
故答案为:.
将方程变形得到,得到a和为一元二次方程的两根,利用根与系数的关系得到,,代入代数式进行计算,即可得到答案.
33.①②③
34.
35.-1
解:,
,
,
解得:,
∴.
故答案为:.
根据二次根式非负性,偶次方的非负性求出,再代入,计算求解即可.
36.,
37.;或
38.
39.
40.①②④
41.4.8
解:∵两条直角边长分别是6和8,
∴斜边为,
设斜边上的高为h,
∴,
即h=4.8.
故答案为:4.8.
根据勾股定理求出斜边的长,根据面积相等,利用三角形的面积公式得到,即可求出斜边上的高.
42.3
43.菱形;
44.
45.64
46.;
47.
解:∵ 关于x的一元二次方程的一个解是,
∴a-b+1=0,
∴a-b=-1,
∴2024+a-b=2024-1=2023.
故答案为:2023.
根据题意可得a-b+1=0,变形得到a-b=-1,将其代入2024+a-b进行计算,即可得到答案.
48.4或5
49.②④
50.
同课章节目录
