云南省昆明市第二十一中学人教版九年级数学上册:24-2-1点和圆的位置关系 教案(无答案)
文档属性
| 名称 | 云南省昆明市第二十一中学人教版九年级数学上册:24-2-1点和圆的位置关系 教案(无答案) |
|
|
| 格式 | zip | ||
| 文件大小 | 17.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-05-20 11:18:20 | ||
图片预览

文档简介
《点和圆的位置关系》教案
一.学习目标:
1.理解点和圆的三种位置关系,并会运用它解决一
些实际问题;
2.会过不在同一直线上的三个点作圆,理解三角形 的
外心和外接圆的概念
3.结合本节内容的学习,体会数形结合、分类讨论 的数学思想.
二.学习重点:
点和圆的位置关系.
教学过程:
一.导入新知:多媒体出示射击靶的图片,利用上面射击点和圆环的 位置关系,引出课题且板书课题。
二.探究新知:
1.请同学黑板上摆出点与圆的所有位置关系。
2. 多媒体出示动画点与圆的所有位置关系。
3.师生归纳点与圆的所有位置关系。
设⊙O 的半径为 r,点 P 到圆心的距离为 d,则有:
点 P 在圆外 d>r ;
点 P 在圆上 d=r ;
点 P 在圆内 d<r .
4.作圆:已知圆心和半径,可以作一个圆.
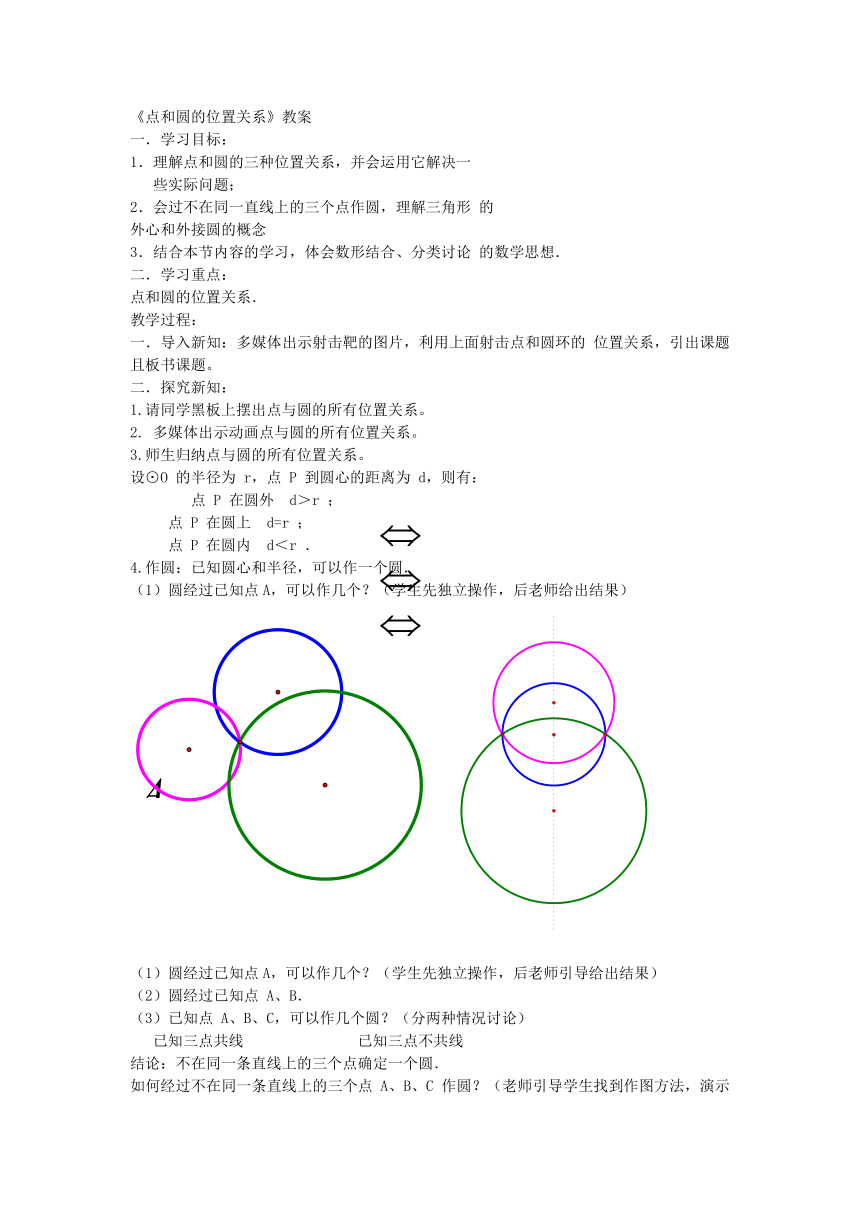
(1)圆经过已知点A,可以作几个?(学生先独立操作,后老师给出结果)
(1)圆经过已知点A,可以作几个?(学生先独立操作,后老师引导给出结果)
(2)圆经过已知点 A、B.
(3)已知点 A、B、C,可以作几个圆?(分两种情况讨论)
已知三点共线 已知三点不共线
结论:不在同一条直线上的三个点确定一个圆.
如何经过不在同一条直线上的三个点 A、B、C 作圆?(老师引导学生找到作图方法,演示作图过程)
①连接 AB、BC;
② 分别作线段 AB、BC 的垂直平分线DE 和 FG,DE 和FG 相交于点 O;
③ 以点O 为圆心,OA 为半径作圆,⊙O 就是所要求作的圆.
(4)归纳概念:
经过三角形的三个顶点可以作一个圆,这个圆叫做三角圆.
外接圆的圆心是三角形三条边的垂直平分线的交点,叫做这个三角形的外心.
三。例题讲解:
例1 已知⊙O 的半径为 5,圆心 O的坐标为 (0,0),若点 P 的坐标为(4,2),点 P 与⊙O 的位置关系是( ).
A.点 P 在⊙O 内 B.点 P 在⊙O上
C.点 P 在⊙O 外 D.点 P 在⊙O 上或⊙O 外
例2 直角三角形的外心是______的中点, 锐角三角形的外心在三角形______,钝角三角形的外心在三角形_________.
四.课堂小结
(1)点和圆的位置关系:
设⊙O 的半径为 r,点 P 到圆心的距离为 d,则
点 P 在圆外 d>r;
点 P 在圆上 d=r;
点 P 在圆内 d<r.
(2)不在同一条直线上的三个点确定一个圆.
(3)理解三角形外接圆和三角形外心的概念.
(五).布置作业
教科书第 95 页 练习第 2,3 题.
A
A
B
C
O
一.学习目标:
1.理解点和圆的三种位置关系,并会运用它解决一
些实际问题;
2.会过不在同一直线上的三个点作圆,理解三角形 的
外心和外接圆的概念
3.结合本节内容的学习,体会数形结合、分类讨论 的数学思想.
二.学习重点:
点和圆的位置关系.
教学过程:
一.导入新知:多媒体出示射击靶的图片,利用上面射击点和圆环的 位置关系,引出课题且板书课题。
二.探究新知:
1.请同学黑板上摆出点与圆的所有位置关系。
2. 多媒体出示动画点与圆的所有位置关系。
3.师生归纳点与圆的所有位置关系。
设⊙O 的半径为 r,点 P 到圆心的距离为 d,则有:
点 P 在圆外 d>r ;
点 P 在圆上 d=r ;
点 P 在圆内 d<r .
4.作圆:已知圆心和半径,可以作一个圆.
(1)圆经过已知点A,可以作几个?(学生先独立操作,后老师给出结果)
(1)圆经过已知点A,可以作几个?(学生先独立操作,后老师引导给出结果)
(2)圆经过已知点 A、B.
(3)已知点 A、B、C,可以作几个圆?(分两种情况讨论)
已知三点共线 已知三点不共线
结论:不在同一条直线上的三个点确定一个圆.
如何经过不在同一条直线上的三个点 A、B、C 作圆?(老师引导学生找到作图方法,演示作图过程)
①连接 AB、BC;
② 分别作线段 AB、BC 的垂直平分线DE 和 FG,DE 和FG 相交于点 O;
③ 以点O 为圆心,OA 为半径作圆,⊙O 就是所要求作的圆.
(4)归纳概念:
经过三角形的三个顶点可以作一个圆,这个圆叫做三角圆.
外接圆的圆心是三角形三条边的垂直平分线的交点,叫做这个三角形的外心.
三。例题讲解:
例1 已知⊙O 的半径为 5,圆心 O的坐标为 (0,0),若点 P 的坐标为(4,2),点 P 与⊙O 的位置关系是( ).
A.点 P 在⊙O 内 B.点 P 在⊙O上
C.点 P 在⊙O 外 D.点 P 在⊙O 上或⊙O 外
例2 直角三角形的外心是______的中点, 锐角三角形的外心在三角形______,钝角三角形的外心在三角形_________.
四.课堂小结
(1)点和圆的位置关系:
设⊙O 的半径为 r,点 P 到圆心的距离为 d,则
点 P 在圆外 d>r;
点 P 在圆上 d=r;
点 P 在圆内 d<r.
(2)不在同一条直线上的三个点确定一个圆.
(3)理解三角形外接圆和三角形外心的概念.
(五).布置作业
教科书第 95 页 练习第 2,3 题.
A
A
B
C
O
同课章节目录
