人教版八年级数学下册18.2.2 菱形 复习题(含详解)
文档属性
| 名称 | 人教版八年级数学下册18.2.2 菱形 复习题(含详解) |

|
|
| 格式 | docx | ||
| 文件大小 | 1.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-03-31 09:05:33 | ||
图片预览




文档简介
18.2.2 菱形复习题
一、单选题
1.我们知道,菱形的性质:“菱形的对角线互相垂直”是真命题,但它的逆命题“对角线互相垂直的四边形是菱形”是假命题,下列图形可作为判断该逆命题是假命题的反例( )
A. B. C. D.
2.菱形和矩形都是特殊的平行四边形,那么下列是菱形和矩形都具有的性质是( )
A.各角都相等 B.各边都相等
C.有两条对称轴 D.对角线相等
3.如图,菱形的边长为2,边在轴上,,对角线、相交于点,则点的坐标是( )
A. B. C. D.
4.将两个完全相同的菱形按如图方式放置,若,,则( )
A. B. C. D.
5.矩形ABCD中,AD=3,AB=9,点E、F同时分别从点A、C出发沿AB、CD方向以每秒1个单位的速度运动,当四边形EBFD为菱形时,两点运动的时间为( )
A.秒 B.秒 C.秒 D.秒
6.如图,是的角平分线,垂直平分,且交于点D,判断以下结论错误的是( )
A. B.
C.是的平分线 D.四边形是矩形
7.小雨在参观故宫博物馆时,被太和殿窗棂的三交六椀菱花图案所吸引,他从中提取出一个含角的菱形(如图1所示).若的长度为,则菱形的面积为( )
A. B. C. D.
8.在菱形ABCD中,点O为对角线AC的中点,点E为AB边上一动点(点E不与点A,B重合),连接EO并延长交CD于点F,连接AF,CE,若四边形AECF一定不是矩形,则∠BAD应满足的条件是( )
A.0°<∠BAD≤90° B.45°<∠BAD≤135°
C.90°<∠BAD<180° D.0°<∠BAD<180°
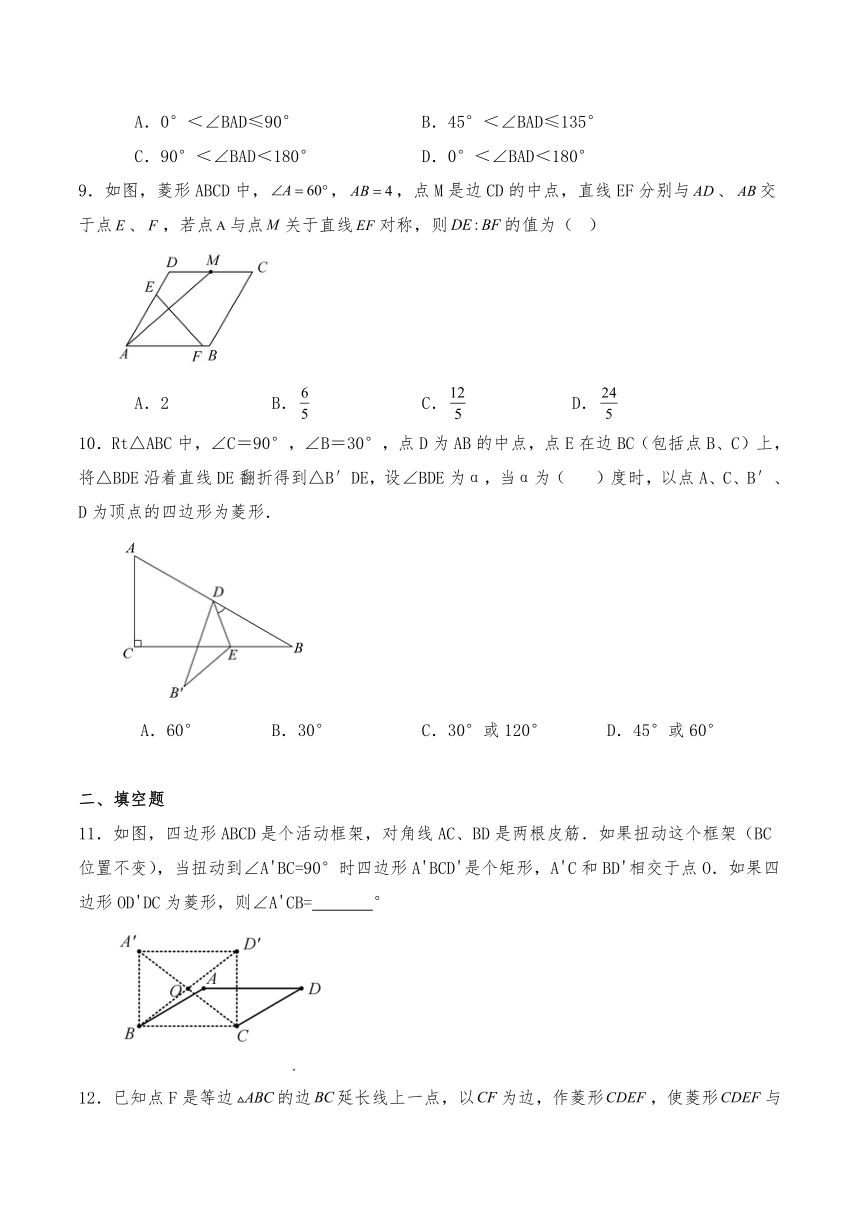
9.如图,菱形ABCD中,,,点M是边CD的中点,直线EF分别与、交于点、,若点与点关于直线对称,则的值为( )
A.2 B. C. D.
10.Rt△ABC中,∠C=90°,∠B=30°,点D为AB的中点,点E在边BC(包括点B、C)上,将△BDE沿着直线DE翻折得到△B′DE,设∠BDE为α,当α为( )度时,以点A、C、B′、D为顶点的四边形为菱形.
A.60° B.30° C.30°或120° D.45°或60°
二、填空题
11.如图,四边形ABCD是个活动框架,对角线AC、BD是两根皮筋.如果扭动这个框架(BC位置不变),当扭动到∠A'BC=90°时四边形A'BCD'是个矩形,A'C和BD'相交于点O.如果四边形OD'DC为菱形,则∠A'CB= °
12.已知点F是等边的边延长线上一点,以为边,作菱形,使菱形与等边在的同侧,且,连结,若的面积为 .
13.如图,四边形是菱形,,是边上的动点,交边于点.当线段最短时,.此时点到直线的距离是 .
14.如图,四边形为菱形,,延长到,在内作射线,使得,过点作,垂足为,若,则对角线的长为 .(结果保留根号)
15.如图,线段,在线段上有一点C,当时,以为直角边在上方作等腰,,P为平面内一点,连接,,将和分别沿,翻折得到和,若A、、P恰好共线,则线段的最小值是 .
16.如图,在菱形中,点为边上一点,点为边中点,连接,将沿直线翻折至菱形所在平面内,得到,连接并延长交边于点.若,,点到线段的距离为,则折痕的长为 .
17.两张完全相同的长方形ABCD、EFGH纸条,长、宽分别为12cm、5cm,按如图所示的方式摆放(对角线BD、EG重合),则重叠部分的四边形BPDQ的对角线QP的长是 cm.
18.如图,四边形为菱形,,,点为边上一点.且,过作交、于点、,连接,若点,分别为、的中点,则的长度为 .
三、解答题
19.如图,菱形,E是的中点,且,.
(1)求的度数; (2)求对角线的长.
20.如图,在四边形中,,E为的中点,连接,,∠ABD=90°;
(1)求证:四边形为菱形.
(2)连接,若,求的长.
21.如图,四边形的对角线,相交于点,,为矩形对角线,,.
(1)求证:四边形是菱形;
(2)连接,若,,求的值.
22.在中,,点D为射线上一动点(点D不与B,C重合),以为边作菱形,使,连接.
(1)如图1,当点D在线段上时,直接写出线段与的数量关系;
(2)如图2,当点D在线段BC的延长线上,且时,求证:.
23.如图,中,是上一点,于点是的中点,于点,与交于点,若平分,连接.
(1)求证:;
(2)试探究线段之间的数量关系,并证明.
(3)若点为中点,判断四边形是什么四边形?并说明理由.
24.在菱形中,,点是平面内一动点,以为边作等边 APE,其中,,按逆时针方向排列.
(1)如图①,当点在线段上,点在菱形内部时,连接,则线段与的数量关系是 ;与的夹角度数是 ;
(2)如图②,当点在线段上,点在菱形外部时,连接,求证:;
(3)如图③,当点在线段的延长线上时,连接,请直接用等式表示线段,,之间的数量关系: .
答案:
一、单选题
1.D
【分析】根据菱形的判定定理判断即可.
解:A、对角线不垂直,不能判断该逆命题是假命题,不符合题意;
B、对角线不垂直,不能判断该逆命题是假命题,不符合题意;
C、对角线互相垂直,但四边形是菱形,不能判断该逆命题是假命题,不符合题意;
D、对角线互相垂直,但四边形不是菱形,能作为判断该逆命题是假命题的反例,符合题意;
故选:D.
2.C
【分析】根据矩形的性质与菱形的性质,找出相同的性质即可.
解:∵矩形的性质为:对边平行且相等,四个角都是90°,对角线互相平分且相等,有两条对称轴;
菱形的性质为:四边相等,对边平行,对角相等,对角线互相垂直且平分,每条对角线平分一组对角,有两条对称轴;
∴菱形和矩形都具有的性质是:对边平行且相等,对角线互相平分,有两条对称轴;
故选C.
3.B
【分析】根据菱形性质,求出两点的坐标,再利用中点坐标公式即可得到点的坐标.
解:过作轴于,如图所示:
菱形的边长为2,边在轴上,,
,,
,
菱形的对角线、相交于点,
点的坐标是,即,
故选:B.
4.D
【分析】由题意可得,由菱形的性质可得,由平行线的性质可得,进行计算即可得到答案.
解:根据题意可得:,
四边形为菱形,
,
,
,
,
故选:D.
5.A
【分析】设t秒时四边形EBFD为菱形,根据菱形的性质得到DE=DF=FB=BE,然后表示出AE=t,DF=9-t,从而根据勾股定理列出方程求解即可.
解:设t秒时四边形EBFD为菱形,
此时DE=DF=FB=BE,
则AE=t,DF=9-t,
根据勾股定理得:,
解得:t=4,
即当四边形EBFD为菱形时,两点运动的时间为4秒,故A正确.
故选:A.
6.D
【分析】根据角平分线,可以的∠MAP=∠NAP,根据垂直平分线,可以证AN=PN,MA=PM,再证明出四边形AMPN为菱形即可得出结果.
解:∵垂直平分,
∴,,
∵平分,∴,
∵,∴,
∴,∴,
同理可知,
∴四边形是平行四边形,
又∵,
∴平行四边形是菱形,
∴,是的平分线.
综上所述,选项A、B、C结论正确,不符合题意.
故选:D.
7.B
【分析】作出图形,利用直角三角形的性质求出高,利用菱形的面积公式可求解.
解:如图所示,菱形中,,,
过点A作于点E,则,
∴,
由勾股定理得,
∴菱形的面积为,
故选:B.
8.A
【分析】根据四边形AECF一定不是矩形得到∠EAF≠90°,又点E不与A、B重合,∠EAF<∠BAD,即可求得∠BAD应满足的条件.
解:如图所示,
∵ 四边形AECF一定不是矩形
∴ ∠EAF≠90°
∵点E不与A、B重合
∴∠EAF<∠BAD
∴当时,,
故选:A
9.C
【分析】利用勾股定理得出的长,再利用菱形的性质以及等边三角形的性质得出,进而得出答案.
解:如图所示:延长,过点作于点,连接,,,
,四边形是菱形,
,
,
设,则,,
,
,
,
解得:,
故,
连接,
,,
是等边三角形,
是的中点,
,
,,
,
设,则,
故,
解得:,
的值为:.
故选:C.
10.C
【分析】分为菱形点对角线,菱形的边长两种情况讨论即可
解:∵Rt△ABC中,∠C=90°,∠B=30°,点D为AB的中点,
∴,
是等边三角形
折叠
①如图,当为菱形的边长时,
,则
②当为菱形的对角线时,此时与重合,如图
同理可得,则
故选C
二、填空题
11.30
【分析】先证明是等边三角形,得到,再由四边形是矩形,得到,则.
解:∵四边形OD'DC为菱形,
∴,
∵在扭动过程中,CD的长度是不会发生变化的,
∴,
∴,
∴是等边三角形,
∴,
∵四边形是矩形,
∴,
∴,
故答案为:30.
12.
【分析】作EH⊥BF延长线于H点,根据菱形以及等边三角形的性质推出∠EFH=60°,结合边长即可求出EH的长度,从而根据BF和EG求出△BEF的面积即可.
解:如图所示,作EH⊥BF延长线于H点,则∠EHF=90°,
∵△ABC为等边三角形,四边形CDEF为菱形,CD∥AB,
∴∠ABC=60°,CD∥EF,
∴∠ABC=∠DCF=∠EFH=60°,∠FEH=30°,
∵EF=8,
∴CF=EF=8,FH=4,EH=4,
∴BF=BC+CF=18,
∴,
故答案为:.
13.2
【分析】利用菱形的性质得到∠ABC=60°,BD平分∠ADC和∠ABC,,则∠DBC=30°,根据垂线段最短可判断当AM⊥BC时,AM最短,则根据含30度的直角三角形三边的关系计算出AM=3,则AN=2,然后根据角平分线的性质得到点N到CD直线的距离等于NA的长.
解:∵四边形ABCD是菱形,∠DAB=120°,
∵AD∥BC, BD平分∠ADC和∠ABC,
∴∠ABC=60°,
∴∠DBC=30°,
当AM⊥BC时,AM最短, 则
∵NM=1,
∴
∴
∴AN=AM-NM=3-1=2,
∵,AM⊥BC,
∴AM⊥AD,
∵BD平分∠ADC,
∴点N到CD的距离等于N点到AD的距离, 而NA=2,
∴此时点N到CD直线的距离是2.
故答案为:2.
14.
【分析】先由菱形的性质得出,求得,再根据直角三角形两锐角互余得 ,连接AC交BD于点O,根据菱形的性质得,,根据AAS证明可得,从而可求出.
解:连接AC,如图,
∵四边形ABCD是菱形,
∴AB//CD,,BD=2DO
∴
∵
∴
∵
∴
∵四边形ABCD是菱形,
∴
∴
在和中,
∴≌
∴
∴
故答案为:.
15.
【分析】由题意可知,当P、、D在同一直线上时,最小,此时,连接交于点O,在上取E,使得,连接、,先利用折叠的性质,证明四边形是菱形,推出是的中位线,得到是的中点,然后利用勾股定理,求得,再根据折叠的性质,得到是的中点,推出是的中位线,求得,最后利用即可求出的最小值.
解:当P、、D构成三角形时,;当P、B、D在同一直线上时,,
,
故当P、、D在同一直线上时,最小,,
如图,连接交于点O,在上取E,使得,连接、,
由折叠的性质可知,,,
对角线、互相垂直平分,
四边形是菱形,
,,
,
∴AC=AB-BC=4,
,
是的中位线,
是的中点,
是等腰直角三角形,
,,
由勾股定理得:,
由折叠性质可知,,,
,
是的中点,
是的中位线,
,
,
故答案为:.
16.
【分析】作,,根据角之间的关系得到,根据勾股定理求得、的长度,从而求得的长度.
解:作,,如下图:
由题意可得:,,,,,
∴,
又∵,
∴
∴
∴四边形为平行四边形
又∵
∴平行四边形为矩形
∴,
由勾股定理得:,即
∵为的中点
∴
∵
∴
由勾股定理得:
故答案为
17.
【分析】由题意得出∠A=∠F=90°,AB=FB,AD=FD,即可证明△ABD≌△FBD,得到∠ADB=∠FDB,进而得到DP=BP,根据AD∥BC,BH∥DF,证四边形BPDQ是菱形,根据勾股定理求出BD,设BP=DP=x,则CP=12﹣x,在Rt△CDP中,由勾股定理得出方程,解方程求出BP,再利用菱形面积的两种求法即可得出答案.
解:∵四边形ABCD、EFGH是完全相同的矩形,
∴∠A=∠F=90°,AB=FB,AD=FD,
在△ABD和△FBD中,
,
∴△ABD≌△FBD(SAS),
∴∠ADB=∠FDB,
∵AB∥CD,DF∥BH,
∴四边形BPDQ是平行四边形,∠ADB=∠PBD,
∴∠FDB=∠PBD,
∴DP=BP,
∴ BPDQ是菱形,
∵长方形ABCD长、宽分别为12cm、5cm,
∴BD===13,
设DP=BP=x,则CP=12﹣x,
在Rt△CDP中,CD2+CP2=DP2,即52+(12﹣x)2=x2,
解得:x=,即BP=,
∴菱形BPDQ的面积=BP CD=×5=,
∵菱形BPDQ的面积=BD QP,
∴×13 QP=,
∴QP=(cm),
故答案为:.
18.
【分析】如图,连接 交于, 连接 过作于 先证明 是等边三角形,求解 证明四边形是平行四边形,可得再求解 再求解 可得 再利用勾股定理可得答案.
解:如图,连接 交于, 连接 过作于
四边形是菱形,
是等边三角形,
四边形是平行四边形,
是的中点,
为等边三角形,
是的中点,
故答案为:
三、解答题
19.
(1)解:如图,连接,
∵四边形是菱形,,
,
是的中点,且,
垂直平分,
,
,
是等边三角形,
,
又,
.
(2)解:如图,连接,交于点,
∵四边形是菱形,,
,
,
.
20.
解:(1)证明:∵,E是的中点,
∴,
∵,
∴,
∵,
∴四边形为平行四边形,
∵,
∴四边形为菱形;
(2)解:连接,如图所示,
由(1)得:四边形为菱形,
∴,
∵,
∴四边形为平行四边形,
∵,
∴四边形为菱形,
∴,
∵,
∴.
21.
解:(1)明:四边形是矩形,
,,
,
,
,
,
四边形是菱形;
(2)解:四边形是菱形,,
,,,,,,
是等边三角形,
,
,
,
四边形是矩形,
,,
.
22.
解:(1)证明:四边形是菱形,
,
,
,
,
≌,
.
(2)证明:四边形是菱形,
,
,
,
,
≌,
,
,,
∴由勾股定理,得,
,
.
23.
解:(1)证明:∵,
∴,
∵平分,
∴,
∴,
∴,
∵,
∴,
∵,
∴,
∴,
∴,,
∵是的中点,,
∴在中,是的中点,
∴是线段的垂直平分线,
∴;
(2),理由如下,
证明:过点作于,
∴,
在和中,
,
∴,
∴,,由(1)可得,
在和中,
∴,
∴,
∴.
(3)解:四边形是菱形,理由如下:
证明:∵在中,为中点,
∴,
∵是线段的垂直平分线,
∴,
∴,
∴四边形是菱形.
24.
(1)解:如图①,连接,延长交于点,与的交点为,
四边形是菱形,
,
,
是等边三角形,
,;
是等边三角形,
,,
,
,
;
四边形是菱形,
,
,
,
,
,
四边形为菱形,
,
为菱形的对角线,
,
;
故答案为:,;
(2)证明:如图②中,连接,交于,
菱形,,
和都是等边三角形,
,,,
是等边三角形,
,,
,
,
,
,
菱形的对角线与相交于,
,,
在中,,
;
(3)解:.
理由:如图③,连接,交于,
同(2)的方法得,,
同(1)的方法得,
.
故答案为:.
一、单选题
1.我们知道,菱形的性质:“菱形的对角线互相垂直”是真命题,但它的逆命题“对角线互相垂直的四边形是菱形”是假命题,下列图形可作为判断该逆命题是假命题的反例( )
A. B. C. D.
2.菱形和矩形都是特殊的平行四边形,那么下列是菱形和矩形都具有的性质是( )
A.各角都相等 B.各边都相等
C.有两条对称轴 D.对角线相等
3.如图,菱形的边长为2,边在轴上,,对角线、相交于点,则点的坐标是( )
A. B. C. D.
4.将两个完全相同的菱形按如图方式放置,若,,则( )
A. B. C. D.
5.矩形ABCD中,AD=3,AB=9,点E、F同时分别从点A、C出发沿AB、CD方向以每秒1个单位的速度运动,当四边形EBFD为菱形时,两点运动的时间为( )
A.秒 B.秒 C.秒 D.秒
6.如图,是的角平分线,垂直平分,且交于点D,判断以下结论错误的是( )
A. B.
C.是的平分线 D.四边形是矩形
7.小雨在参观故宫博物馆时,被太和殿窗棂的三交六椀菱花图案所吸引,他从中提取出一个含角的菱形(如图1所示).若的长度为,则菱形的面积为( )
A. B. C. D.
8.在菱形ABCD中,点O为对角线AC的中点,点E为AB边上一动点(点E不与点A,B重合),连接EO并延长交CD于点F,连接AF,CE,若四边形AECF一定不是矩形,则∠BAD应满足的条件是( )
A.0°<∠BAD≤90° B.45°<∠BAD≤135°
C.90°<∠BAD<180° D.0°<∠BAD<180°
9.如图,菱形ABCD中,,,点M是边CD的中点,直线EF分别与、交于点、,若点与点关于直线对称,则的值为( )
A.2 B. C. D.
10.Rt△ABC中,∠C=90°,∠B=30°,点D为AB的中点,点E在边BC(包括点B、C)上,将△BDE沿着直线DE翻折得到△B′DE,设∠BDE为α,当α为( )度时,以点A、C、B′、D为顶点的四边形为菱形.
A.60° B.30° C.30°或120° D.45°或60°
二、填空题
11.如图,四边形ABCD是个活动框架,对角线AC、BD是两根皮筋.如果扭动这个框架(BC位置不变),当扭动到∠A'BC=90°时四边形A'BCD'是个矩形,A'C和BD'相交于点O.如果四边形OD'DC为菱形,则∠A'CB= °
12.已知点F是等边的边延长线上一点,以为边,作菱形,使菱形与等边在的同侧,且,连结,若的面积为 .
13.如图,四边形是菱形,,是边上的动点,交边于点.当线段最短时,.此时点到直线的距离是 .
14.如图,四边形为菱形,,延长到,在内作射线,使得,过点作,垂足为,若,则对角线的长为 .(结果保留根号)
15.如图,线段,在线段上有一点C,当时,以为直角边在上方作等腰,,P为平面内一点,连接,,将和分别沿,翻折得到和,若A、、P恰好共线,则线段的最小值是 .
16.如图,在菱形中,点为边上一点,点为边中点,连接,将沿直线翻折至菱形所在平面内,得到,连接并延长交边于点.若,,点到线段的距离为,则折痕的长为 .
17.两张完全相同的长方形ABCD、EFGH纸条,长、宽分别为12cm、5cm,按如图所示的方式摆放(对角线BD、EG重合),则重叠部分的四边形BPDQ的对角线QP的长是 cm.
18.如图,四边形为菱形,,,点为边上一点.且,过作交、于点、,连接,若点,分别为、的中点,则的长度为 .
三、解答题
19.如图,菱形,E是的中点,且,.
(1)求的度数; (2)求对角线的长.
20.如图,在四边形中,,E为的中点,连接,,∠ABD=90°;
(1)求证:四边形为菱形.
(2)连接,若,求的长.
21.如图,四边形的对角线,相交于点,,为矩形对角线,,.
(1)求证:四边形是菱形;
(2)连接,若,,求的值.
22.在中,,点D为射线上一动点(点D不与B,C重合),以为边作菱形,使,连接.
(1)如图1,当点D在线段上时,直接写出线段与的数量关系;
(2)如图2,当点D在线段BC的延长线上,且时,求证:.
23.如图,中,是上一点,于点是的中点,于点,与交于点,若平分,连接.
(1)求证:;
(2)试探究线段之间的数量关系,并证明.
(3)若点为中点,判断四边形是什么四边形?并说明理由.
24.在菱形中,,点是平面内一动点,以为边作等边 APE,其中,,按逆时针方向排列.
(1)如图①,当点在线段上,点在菱形内部时,连接,则线段与的数量关系是 ;与的夹角度数是 ;
(2)如图②,当点在线段上,点在菱形外部时,连接,求证:;
(3)如图③,当点在线段的延长线上时,连接,请直接用等式表示线段,,之间的数量关系: .
答案:
一、单选题
1.D
【分析】根据菱形的判定定理判断即可.
解:A、对角线不垂直,不能判断该逆命题是假命题,不符合题意;
B、对角线不垂直,不能判断该逆命题是假命题,不符合题意;
C、对角线互相垂直,但四边形是菱形,不能判断该逆命题是假命题,不符合题意;
D、对角线互相垂直,但四边形不是菱形,能作为判断该逆命题是假命题的反例,符合题意;
故选:D.
2.C
【分析】根据矩形的性质与菱形的性质,找出相同的性质即可.
解:∵矩形的性质为:对边平行且相等,四个角都是90°,对角线互相平分且相等,有两条对称轴;
菱形的性质为:四边相等,对边平行,对角相等,对角线互相垂直且平分,每条对角线平分一组对角,有两条对称轴;
∴菱形和矩形都具有的性质是:对边平行且相等,对角线互相平分,有两条对称轴;
故选C.
3.B
【分析】根据菱形性质,求出两点的坐标,再利用中点坐标公式即可得到点的坐标.
解:过作轴于,如图所示:
菱形的边长为2,边在轴上,,
,,
,
菱形的对角线、相交于点,
点的坐标是,即,
故选:B.
4.D
【分析】由题意可得,由菱形的性质可得,由平行线的性质可得,进行计算即可得到答案.
解:根据题意可得:,
四边形为菱形,
,
,
,
,
故选:D.
5.A
【分析】设t秒时四边形EBFD为菱形,根据菱形的性质得到DE=DF=FB=BE,然后表示出AE=t,DF=9-t,从而根据勾股定理列出方程求解即可.
解:设t秒时四边形EBFD为菱形,
此时DE=DF=FB=BE,
则AE=t,DF=9-t,
根据勾股定理得:,
解得:t=4,
即当四边形EBFD为菱形时,两点运动的时间为4秒,故A正确.
故选:A.
6.D
【分析】根据角平分线,可以的∠MAP=∠NAP,根据垂直平分线,可以证AN=PN,MA=PM,再证明出四边形AMPN为菱形即可得出结果.
解:∵垂直平分,
∴,,
∵平分,∴,
∵,∴,
∴,∴,
同理可知,
∴四边形是平行四边形,
又∵,
∴平行四边形是菱形,
∴,是的平分线.
综上所述,选项A、B、C结论正确,不符合题意.
故选:D.
7.B
【分析】作出图形,利用直角三角形的性质求出高,利用菱形的面积公式可求解.
解:如图所示,菱形中,,,
过点A作于点E,则,
∴,
由勾股定理得,
∴菱形的面积为,
故选:B.
8.A
【分析】根据四边形AECF一定不是矩形得到∠EAF≠90°,又点E不与A、B重合,∠EAF<∠BAD,即可求得∠BAD应满足的条件.
解:如图所示,
∵ 四边形AECF一定不是矩形
∴ ∠EAF≠90°
∵点E不与A、B重合
∴∠EAF<∠BAD
∴当时,,
故选:A
9.C
【分析】利用勾股定理得出的长,再利用菱形的性质以及等边三角形的性质得出,进而得出答案.
解:如图所示:延长,过点作于点,连接,,,
,四边形是菱形,
,
,
设,则,,
,
,
,
解得:,
故,
连接,
,,
是等边三角形,
是的中点,
,
,,
,
设,则,
故,
解得:,
的值为:.
故选:C.
10.C
【分析】分为菱形点对角线,菱形的边长两种情况讨论即可
解:∵Rt△ABC中,∠C=90°,∠B=30°,点D为AB的中点,
∴,
是等边三角形
折叠
①如图,当为菱形的边长时,
,则
②当为菱形的对角线时,此时与重合,如图
同理可得,则
故选C
二、填空题
11.30
【分析】先证明是等边三角形,得到,再由四边形是矩形,得到,则.
解:∵四边形OD'DC为菱形,
∴,
∵在扭动过程中,CD的长度是不会发生变化的,
∴,
∴,
∴是等边三角形,
∴,
∵四边形是矩形,
∴,
∴,
故答案为:30.
12.
【分析】作EH⊥BF延长线于H点,根据菱形以及等边三角形的性质推出∠EFH=60°,结合边长即可求出EH的长度,从而根据BF和EG求出△BEF的面积即可.
解:如图所示,作EH⊥BF延长线于H点,则∠EHF=90°,
∵△ABC为等边三角形,四边形CDEF为菱形,CD∥AB,
∴∠ABC=60°,CD∥EF,
∴∠ABC=∠DCF=∠EFH=60°,∠FEH=30°,
∵EF=8,
∴CF=EF=8,FH=4,EH=4,
∴BF=BC+CF=18,
∴,
故答案为:.
13.2
【分析】利用菱形的性质得到∠ABC=60°,BD平分∠ADC和∠ABC,,则∠DBC=30°,根据垂线段最短可判断当AM⊥BC时,AM最短,则根据含30度的直角三角形三边的关系计算出AM=3,则AN=2,然后根据角平分线的性质得到点N到CD直线的距离等于NA的长.
解:∵四边形ABCD是菱形,∠DAB=120°,
∵AD∥BC, BD平分∠ADC和∠ABC,
∴∠ABC=60°,
∴∠DBC=30°,
当AM⊥BC时,AM最短, 则
∵NM=1,
∴
∴
∴AN=AM-NM=3-1=2,
∵,AM⊥BC,
∴AM⊥AD,
∵BD平分∠ADC,
∴点N到CD的距离等于N点到AD的距离, 而NA=2,
∴此时点N到CD直线的距离是2.
故答案为:2.
14.
【分析】先由菱形的性质得出,求得,再根据直角三角形两锐角互余得 ,连接AC交BD于点O,根据菱形的性质得,,根据AAS证明可得,从而可求出.
解:连接AC,如图,
∵四边形ABCD是菱形,
∴AB//CD,,BD=2DO
∴
∵
∴
∵
∴
∵四边形ABCD是菱形,
∴
∴
在和中,
∴≌
∴
∴
故答案为:.
15.
【分析】由题意可知,当P、、D在同一直线上时,最小,此时,连接交于点O,在上取E,使得,连接、,先利用折叠的性质,证明四边形是菱形,推出是的中位线,得到是的中点,然后利用勾股定理,求得,再根据折叠的性质,得到是的中点,推出是的中位线,求得,最后利用即可求出的最小值.
解:当P、、D构成三角形时,;当P、B、D在同一直线上时,,
,
故当P、、D在同一直线上时,最小,,
如图,连接交于点O,在上取E,使得,连接、,
由折叠的性质可知,,,
对角线、互相垂直平分,
四边形是菱形,
,,
,
∴AC=AB-BC=4,
,
是的中位线,
是的中点,
是等腰直角三角形,
,,
由勾股定理得:,
由折叠性质可知,,,
,
是的中点,
是的中位线,
,
,
故答案为:.
16.
【分析】作,,根据角之间的关系得到,根据勾股定理求得、的长度,从而求得的长度.
解:作,,如下图:
由题意可得:,,,,,
∴,
又∵,
∴
∴
∴四边形为平行四边形
又∵
∴平行四边形为矩形
∴,
由勾股定理得:,即
∵为的中点
∴
∵
∴
由勾股定理得:
故答案为
17.
【分析】由题意得出∠A=∠F=90°,AB=FB,AD=FD,即可证明△ABD≌△FBD,得到∠ADB=∠FDB,进而得到DP=BP,根据AD∥BC,BH∥DF,证四边形BPDQ是菱形,根据勾股定理求出BD,设BP=DP=x,则CP=12﹣x,在Rt△CDP中,由勾股定理得出方程,解方程求出BP,再利用菱形面积的两种求法即可得出答案.
解:∵四边形ABCD、EFGH是完全相同的矩形,
∴∠A=∠F=90°,AB=FB,AD=FD,
在△ABD和△FBD中,
,
∴△ABD≌△FBD(SAS),
∴∠ADB=∠FDB,
∵AB∥CD,DF∥BH,
∴四边形BPDQ是平行四边形,∠ADB=∠PBD,
∴∠FDB=∠PBD,
∴DP=BP,
∴ BPDQ是菱形,
∵长方形ABCD长、宽分别为12cm、5cm,
∴BD===13,
设DP=BP=x,则CP=12﹣x,
在Rt△CDP中,CD2+CP2=DP2,即52+(12﹣x)2=x2,
解得:x=,即BP=,
∴菱形BPDQ的面积=BP CD=×5=,
∵菱形BPDQ的面积=BD QP,
∴×13 QP=,
∴QP=(cm),
故答案为:.
18.
【分析】如图,连接 交于, 连接 过作于 先证明 是等边三角形,求解 证明四边形是平行四边形,可得再求解 再求解 可得 再利用勾股定理可得答案.
解:如图,连接 交于, 连接 过作于
四边形是菱形,
是等边三角形,
四边形是平行四边形,
是的中点,
为等边三角形,
是的中点,
故答案为:
三、解答题
19.
(1)解:如图,连接,
∵四边形是菱形,,
,
是的中点,且,
垂直平分,
,
,
是等边三角形,
,
又,
.
(2)解:如图,连接,交于点,
∵四边形是菱形,,
,
,
.
20.
解:(1)证明:∵,E是的中点,
∴,
∵,
∴,
∵,
∴四边形为平行四边形,
∵,
∴四边形为菱形;
(2)解:连接,如图所示,
由(1)得:四边形为菱形,
∴,
∵,
∴四边形为平行四边形,
∵,
∴四边形为菱形,
∴,
∵,
∴.
21.
解:(1)明:四边形是矩形,
,,
,
,
,
,
四边形是菱形;
(2)解:四边形是菱形,,
,,,,,,
是等边三角形,
,
,
,
四边形是矩形,
,,
.
22.
解:(1)证明:四边形是菱形,
,
,
,
,
≌,
.
(2)证明:四边形是菱形,
,
,
,
,
≌,
,
,,
∴由勾股定理,得,
,
.
23.
解:(1)证明:∵,
∴,
∵平分,
∴,
∴,
∴,
∵,
∴,
∵,
∴,
∴,
∴,,
∵是的中点,,
∴在中,是的中点,
∴是线段的垂直平分线,
∴;
(2),理由如下,
证明:过点作于,
∴,
在和中,
,
∴,
∴,,由(1)可得,
在和中,
∴,
∴,
∴.
(3)解:四边形是菱形,理由如下:
证明:∵在中,为中点,
∴,
∵是线段的垂直平分线,
∴,
∴,
∴四边形是菱形.
24.
(1)解:如图①,连接,延长交于点,与的交点为,
四边形是菱形,
,
,
是等边三角形,
,;
是等边三角形,
,,
,
,
;
四边形是菱形,
,
,
,
,
,
四边形为菱形,
,
为菱形的对角线,
,
;
故答案为:,;
(2)证明:如图②中,连接,交于,
菱形,,
和都是等边三角形,
,,,
是等边三角形,
,,
,
,
,
,
菱形的对角线与相交于,
,,
在中,,
;
(3)解:.
理由:如图③,连接,交于,
同(2)的方法得,,
同(1)的方法得,
.
故答案为:.
