2025年3月浙江省山海联盟中考数学第一次模拟试卷(图片版,含答案)
文档属性
| 名称 | 2025年3月浙江省山海联盟中考数学第一次模拟试卷(图片版,含答案) |

|
|
| 格式 | |||
| 文件大小 | 697.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-03-30 00:00:00 | ||
图片预览



文档简介
2025 年浙江省山海联盟第一次中考模拟数学试卷
一、选择题(本题共有 10 小题,每小题 3 分,共 30 分)
1.在数轴上有分别表示 5,0,1,3四个数的点,其中离原点最远的点表示的数是 ( )
A. 5 B.0 C.1 D.3
2.如图,一颗珠子放在一块木板的正中间,此时几何体的左视图是 ( )
A. B. C. D.
3.2025年 2月 12日,中国载人航天工程办公室宣布,载人月球探测任务的登月服命名为“望字”.已知月
球距离地球的距离约为 384000km,将 384000用科学记数法表示为 ( )
A.3.84 105 B.384 103 C.3.84 103 D. 0.384 106
4.下列运算不正确的是 ( )
A. x2 x2 2x2 B. x x3 x3 C. x6 x2 x4 D. (2x2 )3 8x6
5.在一组数据 24,31,15,26,5■,44中,发现“5■”的个位数字模糊不清,下列统计量中与■的值
无关的是 ( )
A.平均数 B.方差 C.中位数 D.众数
6.关于 x的一元二次方程 x2 4x k 0有实数根,则 k的取值范围是 ( )
A. k 4 B. k 4 C. k 4 D. k 4
7.如图,图形 ABCD在由完全相同的小正方形拼接而成的网格中,顶点 A,B,C,
D均在格点上,则 ABC BCD BAD的值为 ( )
A.120 B.135 C.145 D.150
8.如图,在 Rt△ ABC中, ACB 90 , O是△ ABC的内切圆,若 AC 3.3,
BC 4.4,则图中△ ABO的面积为 ( )
A.5.5 B.2.75 C.6.05 D.3.025
9 4.如图,已知CD x轴,垂足为D,CO,CD分别交反比例函数 y 的图象于点 A,B.若OA AC,
x
则△OBC的面积为 ( )
A.4 B.6 C.8 D.10
第 1 页 共 5 页
10.如图,E,F 分别是正方形 ABCD的边 AD,BC上的点,将正方形纸片 ABCD沿 EF 折叠,使得点 B
的对应点 B 恰好落在边CD上,要想知道正方形 ABCD的边长,只需知道 ( )
A. BF 的长度 B. B CF 的周长 C. B DG的周长 D. A EG的面积
二、填空题(本题共有 6 小题,每小题 3 分,共 18 分)
11.因式分解: x2 x .
12 x x 3.当 时,分式 的值为 0.
x 1
13.如图,扇形OAB的半径为 3cm,且 AOB 45 ,则它的面积为 cm2.
14.如果小球在如图所示的地板上自由的滚动,并随机停留在某块方砖上,那么它最终停留在阴影区域的
概率是 .
(第 14题) (第 15题) (第 16题)
15.如图,在四边形 ABCD中, AD / /BC , ABC 90 ,点 E在 AB的延长线上,DE分别交 BC, AC于
点 F ,G.若 AB 5, AE AD 8, EF DG,则 BC .
16.如图,在 Rt△ ABC中, ABC 90 , tan ACB 4 ,BC 5,D是斜边 AC上的动点,以线段 BD为
3
一边并在其右侧作等边三角形 BDE,连结CE ,则CE 的最小值是 .
三、解答题(本题共有 8 小题,共 72 分.请务必写出解答过程)
17.(8分)计算: 2 sin 45 ( 1)2025 1 ( ) 1.
2
18.(8分)已知 x2 2x 3 0 ,求代数式 (x 1)(2x 1) 5x的值.
第 2 页 共 5 页
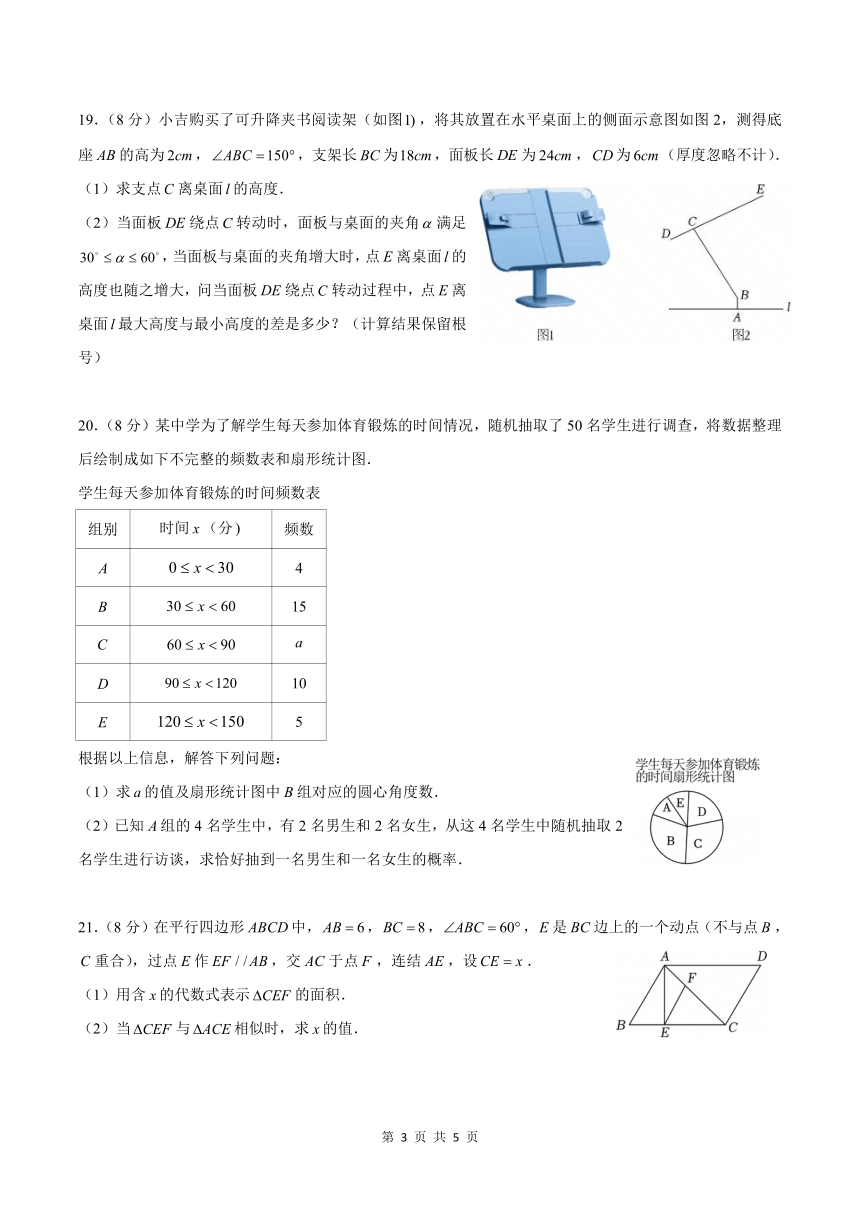
19.(8 分)小吉购买了可升降夹书阅读架(如图1),将其放置在水平桌面上的侧面示意图如图 2,测得底
座 AB的高为 2cm, ABC 150 ,支架长 BC为18cm,面板长DE为 24cm,CD为 6cm(厚度忽略不计).
(1)求支点C 离桌面 l的高度.
(2)当面板DE绕点C转动时,面板与桌面的夹角 满足
30 60 ,当面板与桌面的夹角增大时,点 E离桌面 l的
高度也随之增大,问当面板DE绕点C转动过程中,点 E离
桌面 l最大高度与最小高度的差是多少?(计算结果保留根
号)
20.(8分)某中学为了解学生每天参加体育锻炼的时间情况,随机抽取了 50名学生进行调查,将数据整理
后绘制成如下不完整的频数表和扇形统计图.
学生每天参加体育锻炼的时间频数表
组别 时间 x(分 ) 频数
A 0 x 30 4
B 30 x 60 15
C 60 x 90 a
D 90 x 120 10
E 120 x 150 5
根据以上信息,解答下列问题:
(1)求 a的值及扇形统计图中 B组对应的圆心角度数.
(2)已知 A组的 4名学生中,有 2名男生和 2名女生,从这 4名学生中随机抽取 2
名学生进行访谈,求恰好抽到一名男生和一名女生的概率.
21.(8分)在平行四边形 ABCD中,AB 6,BC 8, ABC 60 ,E是 BC边上的一个动点(不与点 B,
C重合),过点 E作 EF / /AB,交 AC于点 F ,连结 AE,设CE x.
(1)用含 x的代数式表示 CEF 的面积.
(2)当 CEF 与 ACE相似时,求 x的值.
第 3 页 共 5 页
22.(10分)一条公路上有相距80km的 A, B两地,甲、乙、丙三人都在这条公路上匀速行驶.甲从 A地
出发前往 B地,速度为 20km / h.甲出发 1小时后,乙也从 A地出发前往 B地,出发半小时后追上了甲,
到达 B地后停止不动.丙与甲同时出发,从 B地前往 A地,当丙与甲相遇时,甲与乙相距 20km.设甲行驶
的时间为 x(h),甲、乙、丙三人离 A地的距离分别为 y甲 km , y乙 km , y丙 km , y甲, y乙 关于 x的函数
图象如图所示.
(1)求乙的行驶速度.
(2)求甲与乙相距 20km时甲行驶的时间.
(3)丙出发后多少小时与乙相遇?请直接写出答案.
23.(10分)根据以下素材,探索完成任务.
乒乓球发球机的运动路线
素材一 如图 1,某乒乓球台面是矩形,长为 280cm,宽为 150cm,球网高度为
14cm.乒乓球发球机的出球口在桌面中线端点 O正上方 25cm的点 P处.
素材二 假设每次发出的乒乓球都落在中线上,球的运动的高度 y(cm)关于运
动的水平距离 x(m)的函数图象是一条抛物线,且这条抛物线在与点 P
水平距离为 100cm的点 Q处达到最高高度,此时距桌面的高度为 45cm,
乒乓球落在桌面的点 M处.以 O为原点,桌面中线所在直线为 x轴,建
立如图 2所示的平面直角坐标系.
素材三 如图 3,若乒乓球落在桌面上弹起后,在与点 O的水平距离为 300cm的
点 R处达到最高,设弹后球达到最高时距离桌面的高度为 h(cm).
问题解决
任务一 研究乒乓球的飞行轨迹 (1)求出从发球机发球后到落在桌
面前,乒乓球运动轨迹的函数表达
式(不要求写出自变量的取值范
围).
任务二 击球点的确定 (2)当 h=20时,运动员小亮想在
点 R处把球沿直线擦网击打到点 O,
他能不能实现?请说明理由.
第 4 页 共 5 页
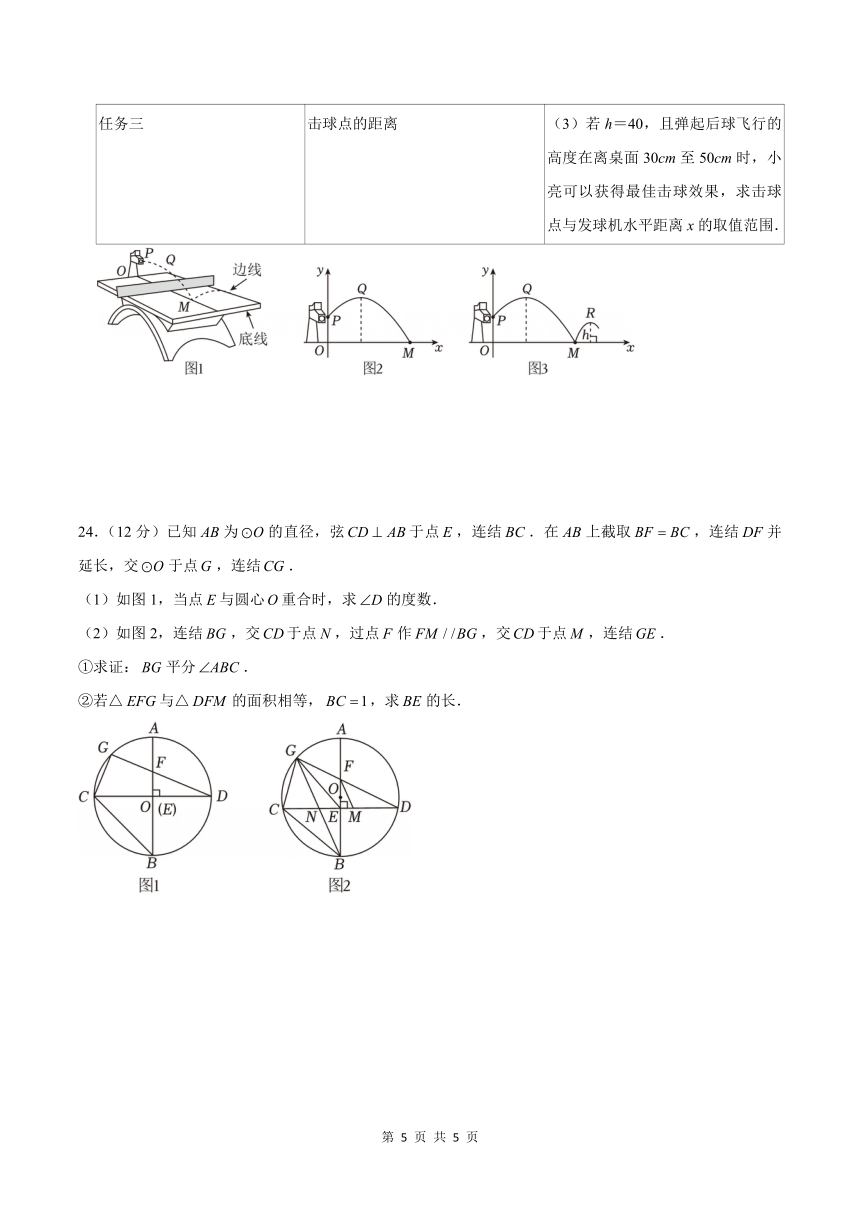
任务三 击球点的距离 (3)若 h=40,且弹起后球飞行的
高度在离桌面 30cm至 50cm时,小
亮可以获得最佳击球效果,求击球
点与发球机水平距离 x的取值范围.
24.(12分)已知 AB为 O 的直径,弦CD AB于点 E,连结 BC.在 AB上截取 BF BC,连结DF 并
延长,交 O 于点G,连结CG.
(1)如图 1,当点 E与圆心O重合时,求 D的度数.
(2)如图 2,连结 BG ,交CD于点 N,过点 F 作 FM / /BG,交CD于点M ,连结GE.
①求证: BG 平分 ABC.
②若△ EFG与△ DFM 的面积相等, BC 1,求 BE 的长.
第 5 页 共 5 页
参考答案与试题解析
一.选择题(共 10 小题)
题号 1 2 3 4 5 6 7 8 9 10
答案 A C A B C B B D B C
9.解:过点 A作 AE x轴于点 E,
CD x 4轴,垂足为D,CO,CD分别交反比例函数 y 的图象于点 A,B,
x
S OAE S
1
OBD 4 2, AE / /CD, OAE ~ OCD,2
OA AC OA 1 S 1 2 , , OAE , S
OC 2 S OCD
8,
OCD 4 S OCD
S OBC S OCD S OBD 8 2 6.
故选: B.
10.解:由折叠得 GB F B 90 , B F BF ,
DB CD B C BC B C,CF B F CF BF BC,BF 2 B C2 B F 2 B C2 CF 2, DB G CFB 90 CB F,
DB G ~ CFB , DB DG B G DB DG B G DB BC B C , ,
CF B C B F CF B C B F CF CF
DB DG B G (BC B C)(BC B
C) BC2 B C2
,
CF CF
BC2 B C2 (BF CF )
2 B C2 BF 2 2BF CF CF 2 B C2 2BF CF 2CF 2
2(BF CF ) 2AB,
CF CF CF CF
DB DG B G 2AB, 要想知道正方形 ABCD的边长,只需知道 B DG的周长;
故选:C.
二、填空题(本题共有 6 小题,每小题 3 分,共 18 分)
11 x(x 1) 12 x 3 13 3 14 1 25 3 3. . . . . . . . 15. . 16. 2.
8 4 3 2
15.解: AD / /BC , ABC 90 , DAE ABC 180 , DAE 90 ,
AD AE 8, AED是等腰直角三角形, DE 2AD 8 2 , E 45 ,
EBF 180 ABC 90 , EBF是等腰直角三角形, FE 2BE,BF BE,
BE AE AB 8 5 3, FE 3 2 , DG EF 3 2, FG ED EF GD 8 2 3 2 3 2 2 2,
FC / /AD 16, CFG ~ ADG, FC : AD FG :GD, FC : 8 2 2 : 3 2 , FC ,
3
BC BF FC 3 16 25 .
3 3
第 6 页 共 5 页
16.解:如图,在 BC的上方作等边△ FBC,连接 AF ,DF,过点 F 作 FH AB于点H .
ABC 90 1 5 , FBC 60 , BC BF CF 5, FH BF ,
2 2
tan ACB AB 4 AB 20 , , AC AB2 BC 2 25 ,
BC 3 3 3
BDE是等边三角形, BE BD, DBE FBC 60 , DBF EBC ,
BDF BEC SAS , DF CE, 当 DF AC 时,DF的值最小,此时CE 的值最小,
S 1 20 5 3 2 1 20 1 25 3 3 ABF S BFC S ABC S ACF , 5 5 DF , DF 2,2 3 2 4 2 3 2 3 2
CE 3 3 的最小值为 2.
2
三、解答题(本题共有 8 小题,共 72 分.请务必写出解答过程)
17 2.解:原式 2 ( 1) ( 2) 1 1 2 2.
2
18.解: x2 2x 3 0, x2 2x 3, (x 1)(2x 1) 5x 2x2 x 2x 1 5x 2(x2 2x) 1 2 3 1 5.
19.解:(1)如图 2中,过点C作CH 直线 l于点H ,过点 B作 BJ CH 于点 J.则四边形 ABJH 是矩形.
JH AB 2cm,
ABC 150 , ABJ 90 , CBJ 60 , CJ BC sin 60 9 3(cm) ,
CH CJ JH (2 9 3)cm, 支点C离桌面 l的高度为 (2 9 3)cm;
(2)如图 2 中,过点 E作 EK 直线 l于点 K,过点C作CG EK于点G,则四边
形CGKH 是矩形, GK CH (2 9 3)cm,
当 ECG 60 时,点 E到直线 l的距离最大,
DE 24cm,CD 6cm, CE DE CD 24 6 18(cm), EG EC sin 60 9 3(cm) ,
EK EG GK (2 18 3)cm.
当 ECG 30 时,点 E到直线 l的距离最小,可得最小值 (11 9 3)cm,
点 E离桌面 l最大高度与最小高度的差 (2 18 3) (11 9 3) (9 3 9)cm.
20.解:(1)由题意得, a 50 4 15 10 5 16.
15
扇形统计图中 B组对应的圆心角度数为 360 108 .
50
第 7 页 共 5 页
(2)列表如下:
男 男 女 女
男 (男,男) (男,女) (男,女)
男 (男,男) (男,女) (男,女)
女 (女,男) (女,男) (女,女)
女 (女,男) (女,男) (女,女)
8 2
共有 12种等可能的结果,其中恰好抽到一名男生和一名女生的结果有 8种, 概率为 .
12 3
21.解:(1)过点 A作 AH BC于点 H .
3 B 60 , AB 6, AH AB sin 60 6 3 3 ,
2
ABC 1的面积 8 3 3 12 3,
2
EF / /AB, ABC ~ FEC ABC的面积 BC, ( )2 64
3
, FEC的面积 x2 (0 x 8);
FEC的面积 EC x 2 16
(2) BH AB cos60 3, CH BC BH 8 3 5, AC 2 AH 2 CH 2 27 25 52,
EF / /AB, B FEC 60 ,
CEF ~ CAE, FEC CAE 60 , CAE B,
ACE ACB, ACB ~ ECA, CA2 CE CB, x CE 52 13 .
8 2
22 1 1.解:(1)设乙的速度为 a km / h,根据题意得: (1 ) 20 a,解得 a 60,
2 2
答:乙的行驶速度为 60km / h;
(2)若甲在乙前面 20km,则此时乙在 A地,甲刚好出发1km,行驶了 20km;
若乙在甲前面 20km,则 (20 1 20) (60 20) 1(h) ,此时甲出发 2h,
综上所述,当甲与乙相距 20km时甲行驶的时间为1h或 2h;
(3)设丙出发 x h与乙相遇,
7
①若甲在乙前面 20km, 丙速度为 (80 20) 1 60(km / h) , 60x 60(x 1) 80 ,解得 x ;
6
②若乙在甲前面 20km,则此时乙在 A地,甲刚好出发1km,行驶了 20km,
(20 1 20) (60 20) 1(h) , 此时乙出发了1h,所走路程为 60km,甲所走路程为 20 (1 1) 40(km) ,
丙的速度为 (80 40) (1 1) 20(km / h), 20x 7 60(x 1) 80 ,解得 x .
4
7 7
综上所述,丙出发 h或 h与乙相遇.
6 4
第 8 页 共 5 页
23.解:任务一:由题意得抛物线的顶点为:(100,45),
设从发球机发球后到落在桌面前,乒乓球运动轨迹的函数表达式为:y=a(x﹣100)2+45,
则 25=a(0 1 1﹣100)2+45,解得 a , y x 100 2 45;
500 500
任务二:小亮不能实现;
1 1
设 OP的解析式为:y=kx,则 300k=20,解得: k , y x,当 x=140时, y 28 <14,
15 15 3
∴小亮不能实现;
1
任务三:设弹起后球飞行的路径为:y=b(x﹣300)2+40,对于 y x 100 2 45,
500
y 0 0 1当 = 时, x 100 2 45,解得:x=﹣50(不合题意,舍去)或 x=250,∴M(250,0),
500
0 b 250 300 2 2∴ = ( ﹣ )2+40,解得:b , y x 300 2 40,
125 125
当 y=30 2时,30 x 300 2 40,解得:x=275或 x=325,
125
∴击球点与发球机水平距离 x的取值范围 275≤x≤325.
24.(1)解:连接 FC,如图,
1点 E与圆心O重合, AB,CD为圆的直径, CD AB, B AOC 45 ,
2
BF BC BCF BFC 180 45 , 67.5 , FCD 22.5 ,
2
CD AB,OC OD, FC FD, D FCD 22.5 ;
(2)①证明:连接 FC, AG, AC,如图, BF BC, BCF BFC,
AB为 O 的直径,弦CD AB于点 E, B C B D, AB垂直平分CD,
CAB DCB,CE DE, FC FD, FDC FCD, FDC GAC, GAC FCD,
GAB GAC CAB, FCB FCD DCB, GAB FCB, GAB BFC , AG / /FC.
AB为 O的直径, AGB 90 , AG BG, FC BG, BC BF, BG平分 ABC;
②连接 FC,AG,AC,过点G作GH AB于点 H ,FC交 BG于点 K,如图,
AB为 O的直径,弦CD AB于点 E, CE DE ,
由(2)①知:BG 平分 ABC, CBG ABG, C G AG, CG AG,
BC BF
在 BCG和 BFG中, CBG FBG, BCG BFG SAS , GC GF , GA GF,
BG BG
GH AB, AH HF.
第 9 页 共 5 页
EFG DFM 1与 的面积相等, EF 1 GH MD EF, GH MD.
2 2
BF BC, BG平分 ABC, CK KF ,
FM / /BG, CN NM 1 CM .
2
DM CD CM 2CE 2CN 2NE, GH 2CE,
GH AB, AB CD, GH / /CD, NE为△GHB的中位线, BE EH ,
设 BE EH x,则 BH 2x,
BC BF 1, FH 2x 1, AH 2x 1, AB BH AH 4x 1.
AB为 O的直径, ACB 90 ,
CD CB AB 1 4x 1 1 17 AB, CEB ~ ABC, , , 4x2 x 1 0 , x .
BE BC x 1 8
经检验,它们都是原方程的根,但负数不合题意,舍去,
BE 1 17 .
8
第 10 页 共 5 页
一、选择题(本题共有 10 小题,每小题 3 分,共 30 分)
1.在数轴上有分别表示 5,0,1,3四个数的点,其中离原点最远的点表示的数是 ( )
A. 5 B.0 C.1 D.3
2.如图,一颗珠子放在一块木板的正中间,此时几何体的左视图是 ( )
A. B. C. D.
3.2025年 2月 12日,中国载人航天工程办公室宣布,载人月球探测任务的登月服命名为“望字”.已知月
球距离地球的距离约为 384000km,将 384000用科学记数法表示为 ( )
A.3.84 105 B.384 103 C.3.84 103 D. 0.384 106
4.下列运算不正确的是 ( )
A. x2 x2 2x2 B. x x3 x3 C. x6 x2 x4 D. (2x2 )3 8x6
5.在一组数据 24,31,15,26,5■,44中,发现“5■”的个位数字模糊不清,下列统计量中与■的值
无关的是 ( )
A.平均数 B.方差 C.中位数 D.众数
6.关于 x的一元二次方程 x2 4x k 0有实数根,则 k的取值范围是 ( )
A. k 4 B. k 4 C. k 4 D. k 4
7.如图,图形 ABCD在由完全相同的小正方形拼接而成的网格中,顶点 A,B,C,
D均在格点上,则 ABC BCD BAD的值为 ( )
A.120 B.135 C.145 D.150
8.如图,在 Rt△ ABC中, ACB 90 , O是△ ABC的内切圆,若 AC 3.3,
BC 4.4,则图中△ ABO的面积为 ( )
A.5.5 B.2.75 C.6.05 D.3.025
9 4.如图,已知CD x轴,垂足为D,CO,CD分别交反比例函数 y 的图象于点 A,B.若OA AC,
x
则△OBC的面积为 ( )
A.4 B.6 C.8 D.10
第 1 页 共 5 页
10.如图,E,F 分别是正方形 ABCD的边 AD,BC上的点,将正方形纸片 ABCD沿 EF 折叠,使得点 B
的对应点 B 恰好落在边CD上,要想知道正方形 ABCD的边长,只需知道 ( )
A. BF 的长度 B. B CF 的周长 C. B DG的周长 D. A EG的面积
二、填空题(本题共有 6 小题,每小题 3 分,共 18 分)
11.因式分解: x2 x .
12 x x 3.当 时,分式 的值为 0.
x 1
13.如图,扇形OAB的半径为 3cm,且 AOB 45 ,则它的面积为 cm2.
14.如果小球在如图所示的地板上自由的滚动,并随机停留在某块方砖上,那么它最终停留在阴影区域的
概率是 .
(第 14题) (第 15题) (第 16题)
15.如图,在四边形 ABCD中, AD / /BC , ABC 90 ,点 E在 AB的延长线上,DE分别交 BC, AC于
点 F ,G.若 AB 5, AE AD 8, EF DG,则 BC .
16.如图,在 Rt△ ABC中, ABC 90 , tan ACB 4 ,BC 5,D是斜边 AC上的动点,以线段 BD为
3
一边并在其右侧作等边三角形 BDE,连结CE ,则CE 的最小值是 .
三、解答题(本题共有 8 小题,共 72 分.请务必写出解答过程)
17.(8分)计算: 2 sin 45 ( 1)2025 1 ( ) 1.
2
18.(8分)已知 x2 2x 3 0 ,求代数式 (x 1)(2x 1) 5x的值.
第 2 页 共 5 页
19.(8 分)小吉购买了可升降夹书阅读架(如图1),将其放置在水平桌面上的侧面示意图如图 2,测得底
座 AB的高为 2cm, ABC 150 ,支架长 BC为18cm,面板长DE为 24cm,CD为 6cm(厚度忽略不计).
(1)求支点C 离桌面 l的高度.
(2)当面板DE绕点C转动时,面板与桌面的夹角 满足
30 60 ,当面板与桌面的夹角增大时,点 E离桌面 l的
高度也随之增大,问当面板DE绕点C转动过程中,点 E离
桌面 l最大高度与最小高度的差是多少?(计算结果保留根
号)
20.(8分)某中学为了解学生每天参加体育锻炼的时间情况,随机抽取了 50名学生进行调查,将数据整理
后绘制成如下不完整的频数表和扇形统计图.
学生每天参加体育锻炼的时间频数表
组别 时间 x(分 ) 频数
A 0 x 30 4
B 30 x 60 15
C 60 x 90 a
D 90 x 120 10
E 120 x 150 5
根据以上信息,解答下列问题:
(1)求 a的值及扇形统计图中 B组对应的圆心角度数.
(2)已知 A组的 4名学生中,有 2名男生和 2名女生,从这 4名学生中随机抽取 2
名学生进行访谈,求恰好抽到一名男生和一名女生的概率.
21.(8分)在平行四边形 ABCD中,AB 6,BC 8, ABC 60 ,E是 BC边上的一个动点(不与点 B,
C重合),过点 E作 EF / /AB,交 AC于点 F ,连结 AE,设CE x.
(1)用含 x的代数式表示 CEF 的面积.
(2)当 CEF 与 ACE相似时,求 x的值.
第 3 页 共 5 页
22.(10分)一条公路上有相距80km的 A, B两地,甲、乙、丙三人都在这条公路上匀速行驶.甲从 A地
出发前往 B地,速度为 20km / h.甲出发 1小时后,乙也从 A地出发前往 B地,出发半小时后追上了甲,
到达 B地后停止不动.丙与甲同时出发,从 B地前往 A地,当丙与甲相遇时,甲与乙相距 20km.设甲行驶
的时间为 x(h),甲、乙、丙三人离 A地的距离分别为 y甲 km , y乙 km , y丙 km , y甲, y乙 关于 x的函数
图象如图所示.
(1)求乙的行驶速度.
(2)求甲与乙相距 20km时甲行驶的时间.
(3)丙出发后多少小时与乙相遇?请直接写出答案.
23.(10分)根据以下素材,探索完成任务.
乒乓球发球机的运动路线
素材一 如图 1,某乒乓球台面是矩形,长为 280cm,宽为 150cm,球网高度为
14cm.乒乓球发球机的出球口在桌面中线端点 O正上方 25cm的点 P处.
素材二 假设每次发出的乒乓球都落在中线上,球的运动的高度 y(cm)关于运
动的水平距离 x(m)的函数图象是一条抛物线,且这条抛物线在与点 P
水平距离为 100cm的点 Q处达到最高高度,此时距桌面的高度为 45cm,
乒乓球落在桌面的点 M处.以 O为原点,桌面中线所在直线为 x轴,建
立如图 2所示的平面直角坐标系.
素材三 如图 3,若乒乓球落在桌面上弹起后,在与点 O的水平距离为 300cm的
点 R处达到最高,设弹后球达到最高时距离桌面的高度为 h(cm).
问题解决
任务一 研究乒乓球的飞行轨迹 (1)求出从发球机发球后到落在桌
面前,乒乓球运动轨迹的函数表达
式(不要求写出自变量的取值范
围).
任务二 击球点的确定 (2)当 h=20时,运动员小亮想在
点 R处把球沿直线擦网击打到点 O,
他能不能实现?请说明理由.
第 4 页 共 5 页
任务三 击球点的距离 (3)若 h=40,且弹起后球飞行的
高度在离桌面 30cm至 50cm时,小
亮可以获得最佳击球效果,求击球
点与发球机水平距离 x的取值范围.
24.(12分)已知 AB为 O 的直径,弦CD AB于点 E,连结 BC.在 AB上截取 BF BC,连结DF 并
延长,交 O 于点G,连结CG.
(1)如图 1,当点 E与圆心O重合时,求 D的度数.
(2)如图 2,连结 BG ,交CD于点 N,过点 F 作 FM / /BG,交CD于点M ,连结GE.
①求证: BG 平分 ABC.
②若△ EFG与△ DFM 的面积相等, BC 1,求 BE 的长.
第 5 页 共 5 页
参考答案与试题解析
一.选择题(共 10 小题)
题号 1 2 3 4 5 6 7 8 9 10
答案 A C A B C B B D B C
9.解:过点 A作 AE x轴于点 E,
CD x 4轴,垂足为D,CO,CD分别交反比例函数 y 的图象于点 A,B,
x
S OAE S
1
OBD 4 2, AE / /CD, OAE ~ OCD,2
OA AC OA 1 S 1 2 , , OAE , S
OC 2 S OCD
8,
OCD 4 S OCD
S OBC S OCD S OBD 8 2 6.
故选: B.
10.解:由折叠得 GB F B 90 , B F BF ,
DB CD B C BC B C,CF B F CF BF BC,BF 2 B C2 B F 2 B C2 CF 2, DB G CFB 90 CB F,
DB G ~ CFB , DB DG B G DB DG B G DB BC B C , ,
CF B C B F CF B C B F CF CF
DB DG B G (BC B C)(BC B
C) BC2 B C2
,
CF CF
BC2 B C2 (BF CF )
2 B C2 BF 2 2BF CF CF 2 B C2 2BF CF 2CF 2
2(BF CF ) 2AB,
CF CF CF CF
DB DG B G 2AB, 要想知道正方形 ABCD的边长,只需知道 B DG的周长;
故选:C.
二、填空题(本题共有 6 小题,每小题 3 分,共 18 分)
11 x(x 1) 12 x 3 13 3 14 1 25 3 3. . . . . . . . 15. . 16. 2.
8 4 3 2
15.解: AD / /BC , ABC 90 , DAE ABC 180 , DAE 90 ,
AD AE 8, AED是等腰直角三角形, DE 2AD 8 2 , E 45 ,
EBF 180 ABC 90 , EBF是等腰直角三角形, FE 2BE,BF BE,
BE AE AB 8 5 3, FE 3 2 , DG EF 3 2, FG ED EF GD 8 2 3 2 3 2 2 2,
FC / /AD 16, CFG ~ ADG, FC : AD FG :GD, FC : 8 2 2 : 3 2 , FC ,
3
BC BF FC 3 16 25 .
3 3
第 6 页 共 5 页
16.解:如图,在 BC的上方作等边△ FBC,连接 AF ,DF,过点 F 作 FH AB于点H .
ABC 90 1 5 , FBC 60 , BC BF CF 5, FH BF ,
2 2
tan ACB AB 4 AB 20 , , AC AB2 BC 2 25 ,
BC 3 3 3
BDE是等边三角形, BE BD, DBE FBC 60 , DBF EBC ,
BDF BEC SAS , DF CE, 当 DF AC 时,DF的值最小,此时CE 的值最小,
S 1 20 5 3 2 1 20 1 25 3 3 ABF S BFC S ABC S ACF , 5 5 DF , DF 2,2 3 2 4 2 3 2 3 2
CE 3 3 的最小值为 2.
2
三、解答题(本题共有 8 小题,共 72 分.请务必写出解答过程)
17 2.解:原式 2 ( 1) ( 2) 1 1 2 2.
2
18.解: x2 2x 3 0, x2 2x 3, (x 1)(2x 1) 5x 2x2 x 2x 1 5x 2(x2 2x) 1 2 3 1 5.
19.解:(1)如图 2中,过点C作CH 直线 l于点H ,过点 B作 BJ CH 于点 J.则四边形 ABJH 是矩形.
JH AB 2cm,
ABC 150 , ABJ 90 , CBJ 60 , CJ BC sin 60 9 3(cm) ,
CH CJ JH (2 9 3)cm, 支点C离桌面 l的高度为 (2 9 3)cm;
(2)如图 2 中,过点 E作 EK 直线 l于点 K,过点C作CG EK于点G,则四边
形CGKH 是矩形, GK CH (2 9 3)cm,
当 ECG 60 时,点 E到直线 l的距离最大,
DE 24cm,CD 6cm, CE DE CD 24 6 18(cm), EG EC sin 60 9 3(cm) ,
EK EG GK (2 18 3)cm.
当 ECG 30 时,点 E到直线 l的距离最小,可得最小值 (11 9 3)cm,
点 E离桌面 l最大高度与最小高度的差 (2 18 3) (11 9 3) (9 3 9)cm.
20.解:(1)由题意得, a 50 4 15 10 5 16.
15
扇形统计图中 B组对应的圆心角度数为 360 108 .
50
第 7 页 共 5 页
(2)列表如下:
男 男 女 女
男 (男,男) (男,女) (男,女)
男 (男,男) (男,女) (男,女)
女 (女,男) (女,男) (女,女)
女 (女,男) (女,男) (女,女)
8 2
共有 12种等可能的结果,其中恰好抽到一名男生和一名女生的结果有 8种, 概率为 .
12 3
21.解:(1)过点 A作 AH BC于点 H .
3 B 60 , AB 6, AH AB sin 60 6 3 3 ,
2
ABC 1的面积 8 3 3 12 3,
2
EF / /AB, ABC ~ FEC ABC的面积 BC, ( )2 64
3
, FEC的面积 x2 (0 x 8);
FEC的面积 EC x 2 16
(2) BH AB cos60 3, CH BC BH 8 3 5, AC 2 AH 2 CH 2 27 25 52,
EF / /AB, B FEC 60 ,
CEF ~ CAE, FEC CAE 60 , CAE B,
ACE ACB, ACB ~ ECA, CA2 CE CB, x CE 52 13 .
8 2
22 1 1.解:(1)设乙的速度为 a km / h,根据题意得: (1 ) 20 a,解得 a 60,
2 2
答:乙的行驶速度为 60km / h;
(2)若甲在乙前面 20km,则此时乙在 A地,甲刚好出发1km,行驶了 20km;
若乙在甲前面 20km,则 (20 1 20) (60 20) 1(h) ,此时甲出发 2h,
综上所述,当甲与乙相距 20km时甲行驶的时间为1h或 2h;
(3)设丙出发 x h与乙相遇,
7
①若甲在乙前面 20km, 丙速度为 (80 20) 1 60(km / h) , 60x 60(x 1) 80 ,解得 x ;
6
②若乙在甲前面 20km,则此时乙在 A地,甲刚好出发1km,行驶了 20km,
(20 1 20) (60 20) 1(h) , 此时乙出发了1h,所走路程为 60km,甲所走路程为 20 (1 1) 40(km) ,
丙的速度为 (80 40) (1 1) 20(km / h), 20x 7 60(x 1) 80 ,解得 x .
4
7 7
综上所述,丙出发 h或 h与乙相遇.
6 4
第 8 页 共 5 页
23.解:任务一:由题意得抛物线的顶点为:(100,45),
设从发球机发球后到落在桌面前,乒乓球运动轨迹的函数表达式为:y=a(x﹣100)2+45,
则 25=a(0 1 1﹣100)2+45,解得 a , y x 100 2 45;
500 500
任务二:小亮不能实现;
1 1
设 OP的解析式为:y=kx,则 300k=20,解得: k , y x,当 x=140时, y 28 <14,
15 15 3
∴小亮不能实现;
1
任务三:设弹起后球飞行的路径为:y=b(x﹣300)2+40,对于 y x 100 2 45,
500
y 0 0 1当 = 时, x 100 2 45,解得:x=﹣50(不合题意,舍去)或 x=250,∴M(250,0),
500
0 b 250 300 2 2∴ = ( ﹣ )2+40,解得:b , y x 300 2 40,
125 125
当 y=30 2时,30 x 300 2 40,解得:x=275或 x=325,
125
∴击球点与发球机水平距离 x的取值范围 275≤x≤325.
24.(1)解:连接 FC,如图,
1点 E与圆心O重合, AB,CD为圆的直径, CD AB, B AOC 45 ,
2
BF BC BCF BFC 180 45 , 67.5 , FCD 22.5 ,
2
CD AB,OC OD, FC FD, D FCD 22.5 ;
(2)①证明:连接 FC, AG, AC,如图, BF BC, BCF BFC,
AB为 O 的直径,弦CD AB于点 E, B C B D, AB垂直平分CD,
CAB DCB,CE DE, FC FD, FDC FCD, FDC GAC, GAC FCD,
GAB GAC CAB, FCB FCD DCB, GAB FCB, GAB BFC , AG / /FC.
AB为 O的直径, AGB 90 , AG BG, FC BG, BC BF, BG平分 ABC;
②连接 FC,AG,AC,过点G作GH AB于点 H ,FC交 BG于点 K,如图,
AB为 O的直径,弦CD AB于点 E, CE DE ,
由(2)①知:BG 平分 ABC, CBG ABG, C G AG, CG AG,
BC BF
在 BCG和 BFG中, CBG FBG, BCG BFG SAS , GC GF , GA GF,
BG BG
GH AB, AH HF.
第 9 页 共 5 页
EFG DFM 1与 的面积相等, EF 1 GH MD EF, GH MD.
2 2
BF BC, BG平分 ABC, CK KF ,
FM / /BG, CN NM 1 CM .
2
DM CD CM 2CE 2CN 2NE, GH 2CE,
GH AB, AB CD, GH / /CD, NE为△GHB的中位线, BE EH ,
设 BE EH x,则 BH 2x,
BC BF 1, FH 2x 1, AH 2x 1, AB BH AH 4x 1.
AB为 O的直径, ACB 90 ,
CD CB AB 1 4x 1 1 17 AB, CEB ~ ABC, , , 4x2 x 1 0 , x .
BE BC x 1 8
经检验,它们都是原方程的根,但负数不合题意,舍去,
BE 1 17 .
8
第 10 页 共 5 页
同课章节目录
