2025年浙江省杭州市西湖区保俶塔申花实验学校3月中考数学模拟试卷(pdf版,含答案)
文档属性
| 名称 | 2025年浙江省杭州市西湖区保俶塔申花实验学校3月中考数学模拟试卷(pdf版,含答案) |  | |
| 格式 | |||
| 文件大小 | 769.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-03-30 16:07:55 | ||
图片预览



文档简介
2025 年保俶塔申花实验学校九年级第二学期
中考数学模拟试卷(3 月份)
一.选择题(本大题共有 10 小题,每小题 3 分,共 30 分,每小题只有一个选项符合题意)
1.下列实数中,无理数是 ( )
A. 3 B 2.0 C. D. 5
3
2.据《人民日报》3月 12日电,世界知识产权组织近日公布数据显示,2023年,全球 PCT (《专利合作条
约》 )国际专利申请总量为 27.26万件,中国申请量为 69610件,是申请量最大的来源国.数据 69610用科
学记数法表示为 ( )
A. 6961 10 B. 696.1 102 C. 6.961 104 D. 0.6961 105
3.如图是由长方体和圆柱组成的几何体,其俯视图是 ( )
A. B. C. D.
4.在下列长度的四条线段中,能与长 6cm,8cm的两条线段围成一个三角形的是 ( )
A.1cm B. 2cm C.13cm D.14cm
5.下列运算正确的是 ( )
A. a3 a3 a9 B. a4 a2 a2 C. (a3)2 a5 D. 2a2 a2 2
6.如图,在 Rt△ ABC中, AC BC 2,点 D在 AB的延长线上,且CD AB,则 BD的长是 ( )
A. 10 2 B. 6 2 C. 2 2 2 D. 2 2 6
7 m m.若双曲线 y 与直线 y nx的一个交点坐标为 ( 1,2),则关于 x的不等式 nx的解集为 ( )
x x
A. 1 x 1 B. x 1或 x 1 C. 1 x 0或 x 1 D. x 1或 0 x 1
8 5.如图,在 ABC中, AB AC BC, AD BC于D, O为 ABC的内切圆,设 O
3
的半径为 R, AD R的长为 h,则 的值为 ( )
h
A 3 B 2 C 1 D 1. . . .
8 7 3 2
9.已知点 P1(x
2
1, y1), P2 (x2, y2 )为抛物线 y ax 4ax c(a 0)上两点,且 x1 x2 ,则下列说法正确的
是 ( )
第 1 页 共 4 页
A.若 x1 x2 4,则 y1 y2 B.若 x1 x2 4,则 y1 y2
C.若 a(x1 x2 4) 0,则 y1 y2 D.若 a(x1 x2 4) 0,则 y1 y2
10.如图,已知正方形 ABCD和正方形 BEFG,且 A、 B、 E三点在一条直线上,连接CE ,以CE 为边构
造正方形CPQE ,PQ交 AB于点M ,连接CM .设 APM , BCM .若点Q、B、F 三点共线,
tan n tan ,则 n的值为 ( )
A 2. B 3.
3 5
C 6. D 12.
7 13
二、填空题:(本大题共 6 小题,每小题 3 分,共 18 分)
11.因式分解: a2 4a .
12.如图,若圆锥的母线长为 12,底面半径为 4,则其侧面展开图的圆心角为 .
13.如图, AD,BE 均为△ ABC的高,且 AB AC,连结DE交 AB于点O,若 C 38 ,则 OEB的度
数为 .
(第 12题) (第 13题) (第 15题) (第 16题)
14.若一元二次方程 2x2 4x 1 0 的两根为m, n,则 3m2 4m n2 的值为 .
15.如图, O 与直线 l相交,圆心O到直线 l的距离OA 3,在直线 l上取点 B使 AB 3,将直线 l绕点
B逆时针旋转15 后得到直线m,若直线m恰好与 O相切于点C,则 O的半径为 .
16.如图,在 ABCD中,点 E是CD边上的一点,若 AB 5,CE 2,将△ BCE 沿 BE 翻折得△ BGE,
连结 AG,点 A在 EG的延长线上, BG恰好平分 ABE ,则 AG的长为 , cos EAD的值为 .
三、解答题:(本大题有 8 小题,共 72 分)
17.(8分)计算:
2
(1) | 1| 3 8 1 ( ) 2 a 2 3 ( 4);(2) .
3 a 1 1 a
18.(8分)某校计划在七年级开展阳光体育锻炼活动,开设以下五个球类项目:A(羽毛球),B(乒乓球),
C(篮球),D(排球),E(足球),要求每位学生必须参加,且只能选择其中一个项目.为了了解学生对
这五个项目的选择情况,学校从七年身全体学生中随机抽取部分学生进行问卷调查,对调查所得到的数据
第 2 页 共 4 页
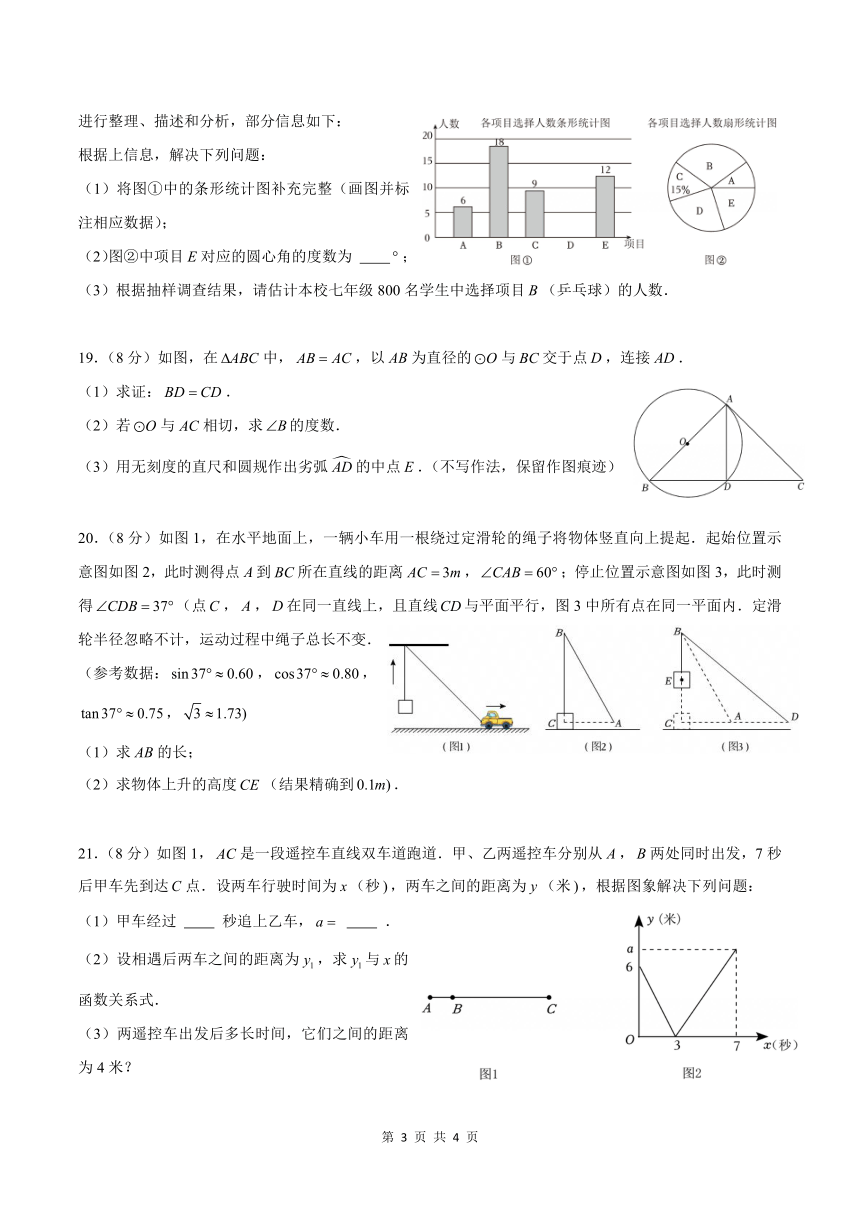
进行整理、描述和分析,部分信息如下:
根据上信息,解决下列问题:
(1)将图①中的条形统计图补充完整(画图并标
注相应数据);
(2)图②中项目 E对应的圆心角的度数为 ;
(3)根据抽样调查结果,请估计本校七年级 800名学生中选择项目 B(乒乓球)的人数.
19.(8分)如图,在 ABC中, AB AC,以 AB为直径的 O与 BC交于点D,连接 AD.
(1)求证: BD CD.
(2)若 O与 AC相切,求 B的度数.
(3)用无刻度的直尺和圆规作出劣弧 AD的中点 E.(不写作法,保留作图痕迹)
20.(8分)如图 1,在水平地面上,一辆小车用一根绕过定滑轮的绳子将物体竖直向上提起.起始位置示
意图如图 2,此时测得点 A到 BC所在直线的距离 AC 3m, CAB 60 ;停止位置示意图如图 3,此时测
得 CDB 37 (点C, A,D在同一直线上,且直线CD与平面平行,图 3中所有点在同一平面内.定滑
轮半径忽略不计,运动过程中绳子总长不变.
(参考数据: sin37 0.60, cos37 0.80,
tan 37 0.75, 3 1.73)
(1)求 AB的长;
(2)求物体上升的高度CE (结果精确到 0.1m).
21.(8分)如图 1, AC是一段遥控车直线双车道跑道.甲、乙两遥控车分别从 A, B两处同时出发,7秒
后甲车先到达C点.设两车行驶时间为 x(秒 ),两车之间的距离为 y(米 ),根据图象解决下列问题:
(1)甲车经过 秒追上乙车, a .
(2)设相遇后两车之间的距离为 y1,求 y1与 x的
函数关系式.
(3)两遥控车出发后多长时间,它们之间的距离
为 4米?
第 3 页 共 4 页
22.(10分)综合与实践
【问题情境】
如图,在正方形 ABCD中,点 E在线段 AD上,点 F 在线段CD上,且始终满足 AE CF ,连接 BE ,BF ,
将线段 BE绕点 E逆时针旋转一定角度,得到线段 EG(点G是点 B旋转后的对应点),并使点G落在线段
BC上, EG与 BF 交于点H .
【初步分析】
(1)线段 EG与 BF的数量关系为 ,位置关系为 ;
【深入分析】
(2)如图②,再将线段 EG绕点 E逆时针旋转90 ,得到线段 EM(点M 是点G旋转后的对应点),连接 FM ,
请判断四边形 BEMF 的形状,并说明理由;
(3)如图③,若点G落在 BC的延长线上,且当点H 恰好为 EG的中点时,设CD与 EG交于点 N,AD 3,
求CG的长.
23.(10分)已知二次函数 y mx2 2mx 3,其中m 0.
(1)若二次函数经过 ( 1,4),求二次函数解析式.
(2)若该抛物线开口向上,当 1 x 2时,抛物线的最高点为M ,最低点为 N,点M 的纵坐标为 9,求
点M 和点 N的坐标.
(3)在二次函数图象上任取两点 (x1 , y1), (x2 , y2 ),当a x1 x2 a 2时,总有 y1 y2,求 a的取值范
围.
24.(12分)在 ABC内接于 O,点D在 O上,连结 AD,AO,分别交 BC于点 E,F , CAD BAO.
(1)求证: AD BC.
(2)若 AO / /CD.
①求证:CA CF .
②若CD 5, BF 10 ,求 BC的长.
第 4 页 共 4 页
参考答案与试题解析
一.选择题(共 10 小题)
题号 1 2 3 4 5 6 7 8 9 10
答案 D C C C B B C A D A
9 4a.解:抛物线对称轴为直线 x 2,当 x1 x 4时, x2a 2 2
2 2 x1,
则当 a 0时, y1 y2;当 a 0时, y1 y2 ;
当 x1 x2 4时, x2 2 2 x1,则当 a 0时, y2 y1;当 a 0时, y1 y2;
故 A、 B选项都不正确;
若 a(x1 x2 4) 0,则 a与 x1 x2 4同号,由上可知 y1 y2,故C不正确;
若 a(x1 x2 4) 0,则 a与 x1 x2 4异号,由上可知 y1 y2,故 D正确;
故选: D.
10.解:过点Q作QN AB于 N,连接Q、B、F ,则 QNE QNM 90 ,
EC EQ,CB CD, GBE CEQ BCD PCE A 90 ,
点Q、B、F 三点共线, QBN EBF 45 , EBF 、 BQN都是等腰直角三角形, QN BN ,
BCE BEC 90 , QEN BEC 90 , BCE QEN ,
ENQ CBE 90
在 ENQ和 CBE 中, QEN BCE , ENQ CBE (AAS ), EN CB,QN EB,
EQ CE
QN BN , EN CB 2EB, EB QN BN BG CG ,
设 EB QN BN BG CG a ,则 AB BC CD AD 2a, AN 2a a a,
DCP BCP 90 , BCE BCP 90 , DCP BCE,
CBE D 90
在 CBE 和 CDP中, CB CD , CBE CDP( ASA), BE DP a, PA 2a a a, PA QN,
BCE DCP
PMA QMN
在 PAM 和 QNM 中, , PAM QNM (AAS), AM MN 1 AN 1 a,BM 2a 1 a 3 A QNM 90 a,
2 2 2 2
PA QN
1 a 3 a
在Rt PAM中, tan APM tan AM 2 1 ,在Rt BCM BM 3中, tan BCM tan 2 ,
PA a 2 BC 2a 4
tan n tan 1 3 2, n , n ,故选: A.
2 4 3
第 5 页 共 4 页
二、填空题:(本大题共 6 小题,每小题 3 分,共 18 分)
11. a(a 4). 12.120 . 13.52 . 14.6. 15. 6 . 16.
15.解:如图所示,连接OB,OC, 圆心O到直线 l的距离OA 3, OA AB,
AB 3 tan ABO AO 3 , , BO AB2 AO2 2 3, ABO 30 ,
AB 3
将直线 l绕点 B逆时针旋转15 后得到的直线m, ABC 15 ,
CBO CBA ABO 45 ,
直线m恰好与 O相切于点C, OC BC, COB 45 , CB CO,CB2 CO2 BO2 ,
2CO2 (2 3)2 , CO 6 , O的半径为 6 .
16.解: 四边形 ABCD是平行四边形, AB / /CD,
将△ BCE沿 BE 翻折得△ BGE, CBE GBE, CEB AEB,CE GE,
设 CBE GBE , BG恰好平分 ABE , ABG GBE CBE , ABE 2 ,
AB / /CD, CEB ABE 2 , AEB ABE 2 , AE AB,
又 CE GE, AG AE GE AB CE 5 2 3;
如图所示,延长 BE交 AD的延长线于点 F ,过点 B分别作 AE, AF 的垂线,垂足分别为H ,M ,
AB AE, AEB ABE 2 , BAE 180 4 ,
BC / /AD,
F CBE , EAD BAD BAE (180 3 ) (180 4 ) ,
F EAF , EF EA 5,
DE CD EF DE 3 5 3 CE AB CE 5 2 3, AB / /DE, △ FED∽△ FBA, , ,
BF AB 5 BE 5
BF 25 BE BF EF 25 5 10 ,则 ,
3 3 3
在 Rt△ ABH ,Rt△ BEH 中,BE2 EH 2 AB2 AH 2 (10, )2 EH 2 52 (5 EH )2 EH 10,解得: ,
3 9
BH BE 2 HE 2 (10则 )2 (10 )2 20 2 ,GH GE EH 2 10 8 ,
3 9 9 9 9
Rt 20 2 8在 △ BGH 中, BG BH 2 GH 2 ( )2 ( )2 4 6 ,
9 9 3
5 20 2
BM HB
BGH C BAM , sin BGH sin BAM , , AB BH 9 25 3 ,
AB BG BM BG 4 6 9
3
第 6 页 共 4 页
25 6
在 Rt△ BMF 中,MF BF 2 BM 2 (5 10)2 (25 3)2 25 6
MF 6
, cos EAD cos F 9 25 ,3 9 9 BF 3
3
6
故答案为: .
3
三、解答题:(本大题有 8 小题,共 72 分)
2
17.解:(1 a 2 3 (a 1)(a 1))原式 1 2 9 4 12;(2)原式 a 1.
a 1 a 1
18.解:(1)此次调查的总人数为 9 15% 60(人 ),D项目的人数有 60 6 18 9 12 15(人 ),
补全条形统计图如下:
(2)图②中项目 E 12对应的圆心角的度数为 360 72 ;
60
故答案为:72;
18
(3)800 240(名 ),
60
答:估计本校七年级 800名学生中选择项目 B(乒乓球)的人数为 240名.
19.(1)证明: AB是直径, ADB 90 , AD BC, AB AC , BD CD;
(2)解: O与 AC相切, AB为直径, BA AC,
AB AC , BAC是等腰直角三角形, B 45 ;
(3)解:如图,作 ABC的角平分线交 AD于点 E,则点 E即是劣弧 AD的中点.
20.解:(1)由题意得: BCA 90 ,
AC AC 3 1 3m, CAB 60 ,在 Rt△ ABC中,由 cos A ,得 cos60 , AB 6m;
AB AB 2
(2)在 Rt△ ABC中,由勾股定理得: BC AB2 AC 2 3 3(m),在 Rt△ BCD中, sin CDB BC ,
BD
sin37 3 3 0.6, BD 5 3m,由题意得, BC AB BE BD,
BD
BE BC AB BD 3 3 6 5 3 6 2 3(m) , CE BC BE 3 3 (6 2 3) 5 3 6 2.7(m) ,
答:物体上升的高度约为 2.7m.
21.解:(1)由图象可知,甲车经过 3秒追上乙车;
甲的速度比乙的速度快 6 3 2(米 /秒),则 7秒时甲、乙之间的距离为 2 (7 3) 8(米 ), a 8.
故答案为:3,8.
(2) y1 2(x 3) 2x 6, y1与 x的函数关系式为 y1 2x 6.
(3)当0 x 3时,当之间的距离为 4米时,得 6 2x 4,解得 x 1;
第 7 页 共 4 页
当3 x 7时,当之间的距离为 4米时,得 2x 6 4,解得 x 5.
答:两遥控车出发后 1秒或 5秒时,它们之间的距离为 4米.
22.解:(1) EG BF, EG BF ;理由如下:
四边形 ABCD是正方形 A C ABC 90 , AB CB,
又 AE CF, ABE CBF (SAS ), BE BF , ABE CBF .
由旋转的性质,得 BE EG, EG BF , EBG EGB.
又 ABE EBG ABC 90 , CBF EGB 90 , BHG 90 ,即 EG BF .
故答案为: EG BF, EG BF ;
(2)四边形 BEMF 为菱形,理由如下:
由旋转的性质,得 EG EM , GEM 90 ,
又 EG BF , BHE 90 , EM BF, GEM BHE 90 , EM / /BF , 四边形 BEMF 是平行四边形,
又 BE BF , 四边形 BEMF 是菱形;
(3) 点H 是 EG的中点, BF EG, BF是 EG的垂直平分线, BE BG, EBF GBF .
ABE CBF ABE CBF EBF 1 1又 , ABC 90 30 .
3 3
四边形 ABCD是正方形, D 90 ,AB AD CD BC 3, 在Rt ABE中,BE AB 3 2 3,
sin 60 3
2
BG 2 3, CG BG BC 2 3 3.
23.解:(1)把 ( 1,4) 1 1 2代入函数解析式得m 2m 3 4, m , 函数解析式为: y x2 x 3;
3 3 3
(2) 抛物线开口方向向上, m 0,
y mx2 2mx 3 m(x 1)2 3 m, 抛物线的顶点为 (1,3 m),
当 x 1时 y随 x增大而减小,当 x 1时, y随 x增大而增大, 最低点 N (1,3 m),
当 x 1时, y 3m 3,当 x 2时, y 3,且m 0, 3m 3 3, 最高点M ( 1,3m 3),
3m 3 9, m 2,代入M 点和 N点坐标得:M ( 1,9), N (1,1);
(3)①当m 0时,
则有当 x 1时 y随 x增大而减小,当 x 1时, y随 x增大而增大,
又 当a x1 x2 a 2时,总有 y1 y2,此时 a 2 1,
a 1,
第 8 页 共 4 页
②当m 0时,
则有当 x 1时 y随 x增大而增大,当 x 1时, y随 x增大而减小,
又 当a x1 x2 a 2时,总有 y1 y2,此时 a 1,
综上,当m 0时 a 1;当m 0时, a 1.
24.(1)证明:延长 AO交 O于点M ,连结CM ,如图,
AM 为 O的直径, ACM 90 , BCM ACE 90 ,
BCM BAO, BAO ACE 90 ,
CAD BAO, CAD ACE 90 ,即 AEC 90 , AD BC;
(2)①证明: AO / /CD, FAE D,
D B, FAE B,
CAF CAE FAE, FAB B AFC,又 CAD BAO,即 CAE FAB,
CAF AFC, CA CF ;
②解: CAD FAB, D B ACD AC CD 5, ∽ AFB, ,
AF BF 10
设 AC 5a,则 AF 10a,由①知CF CA, CF 5a,
设CE x,则 EF 5a x,由(1)知 AD BC, AE 2 AC 2 CE 2 , AE2 AF 2 EF 2,
AC 2 CE 2 AF 2 EF 2 , (5a)2 x2 ( 10a)2 (5a x)2 , x 4a,即CE 4a, EF a,
AE AC2 CE2 (5a)2 (4a)2 3a,
FAE AE EF B, AEF BEA, AEF∽ BEA, ,即 AE2 EF EB,
EB AE
(3a)2 a (a 10) 10 5 10 5 10 13 10 ,解得 a , CF 5a , BC CF BF 10 .
8 8 8 8
第 9 页 共 4 页
中考数学模拟试卷(3 月份)
一.选择题(本大题共有 10 小题,每小题 3 分,共 30 分,每小题只有一个选项符合题意)
1.下列实数中,无理数是 ( )
A. 3 B 2.0 C. D. 5
3
2.据《人民日报》3月 12日电,世界知识产权组织近日公布数据显示,2023年,全球 PCT (《专利合作条
约》 )国际专利申请总量为 27.26万件,中国申请量为 69610件,是申请量最大的来源国.数据 69610用科
学记数法表示为 ( )
A. 6961 10 B. 696.1 102 C. 6.961 104 D. 0.6961 105
3.如图是由长方体和圆柱组成的几何体,其俯视图是 ( )
A. B. C. D.
4.在下列长度的四条线段中,能与长 6cm,8cm的两条线段围成一个三角形的是 ( )
A.1cm B. 2cm C.13cm D.14cm
5.下列运算正确的是 ( )
A. a3 a3 a9 B. a4 a2 a2 C. (a3)2 a5 D. 2a2 a2 2
6.如图,在 Rt△ ABC中, AC BC 2,点 D在 AB的延长线上,且CD AB,则 BD的长是 ( )
A. 10 2 B. 6 2 C. 2 2 2 D. 2 2 6
7 m m.若双曲线 y 与直线 y nx的一个交点坐标为 ( 1,2),则关于 x的不等式 nx的解集为 ( )
x x
A. 1 x 1 B. x 1或 x 1 C. 1 x 0或 x 1 D. x 1或 0 x 1
8 5.如图,在 ABC中, AB AC BC, AD BC于D, O为 ABC的内切圆,设 O
3
的半径为 R, AD R的长为 h,则 的值为 ( )
h
A 3 B 2 C 1 D 1. . . .
8 7 3 2
9.已知点 P1(x
2
1, y1), P2 (x2, y2 )为抛物线 y ax 4ax c(a 0)上两点,且 x1 x2 ,则下列说法正确的
是 ( )
第 1 页 共 4 页
A.若 x1 x2 4,则 y1 y2 B.若 x1 x2 4,则 y1 y2
C.若 a(x1 x2 4) 0,则 y1 y2 D.若 a(x1 x2 4) 0,则 y1 y2
10.如图,已知正方形 ABCD和正方形 BEFG,且 A、 B、 E三点在一条直线上,连接CE ,以CE 为边构
造正方形CPQE ,PQ交 AB于点M ,连接CM .设 APM , BCM .若点Q、B、F 三点共线,
tan n tan ,则 n的值为 ( )
A 2. B 3.
3 5
C 6. D 12.
7 13
二、填空题:(本大题共 6 小题,每小题 3 分,共 18 分)
11.因式分解: a2 4a .
12.如图,若圆锥的母线长为 12,底面半径为 4,则其侧面展开图的圆心角为 .
13.如图, AD,BE 均为△ ABC的高,且 AB AC,连结DE交 AB于点O,若 C 38 ,则 OEB的度
数为 .
(第 12题) (第 13题) (第 15题) (第 16题)
14.若一元二次方程 2x2 4x 1 0 的两根为m, n,则 3m2 4m n2 的值为 .
15.如图, O 与直线 l相交,圆心O到直线 l的距离OA 3,在直线 l上取点 B使 AB 3,将直线 l绕点
B逆时针旋转15 后得到直线m,若直线m恰好与 O相切于点C,则 O的半径为 .
16.如图,在 ABCD中,点 E是CD边上的一点,若 AB 5,CE 2,将△ BCE 沿 BE 翻折得△ BGE,
连结 AG,点 A在 EG的延长线上, BG恰好平分 ABE ,则 AG的长为 , cos EAD的值为 .
三、解答题:(本大题有 8 小题,共 72 分)
17.(8分)计算:
2
(1) | 1| 3 8 1 ( ) 2 a 2 3 ( 4);(2) .
3 a 1 1 a
18.(8分)某校计划在七年级开展阳光体育锻炼活动,开设以下五个球类项目:A(羽毛球),B(乒乓球),
C(篮球),D(排球),E(足球),要求每位学生必须参加,且只能选择其中一个项目.为了了解学生对
这五个项目的选择情况,学校从七年身全体学生中随机抽取部分学生进行问卷调查,对调查所得到的数据
第 2 页 共 4 页
进行整理、描述和分析,部分信息如下:
根据上信息,解决下列问题:
(1)将图①中的条形统计图补充完整(画图并标
注相应数据);
(2)图②中项目 E对应的圆心角的度数为 ;
(3)根据抽样调查结果,请估计本校七年级 800名学生中选择项目 B(乒乓球)的人数.
19.(8分)如图,在 ABC中, AB AC,以 AB为直径的 O与 BC交于点D,连接 AD.
(1)求证: BD CD.
(2)若 O与 AC相切,求 B的度数.
(3)用无刻度的直尺和圆规作出劣弧 AD的中点 E.(不写作法,保留作图痕迹)
20.(8分)如图 1,在水平地面上,一辆小车用一根绕过定滑轮的绳子将物体竖直向上提起.起始位置示
意图如图 2,此时测得点 A到 BC所在直线的距离 AC 3m, CAB 60 ;停止位置示意图如图 3,此时测
得 CDB 37 (点C, A,D在同一直线上,且直线CD与平面平行,图 3中所有点在同一平面内.定滑
轮半径忽略不计,运动过程中绳子总长不变.
(参考数据: sin37 0.60, cos37 0.80,
tan 37 0.75, 3 1.73)
(1)求 AB的长;
(2)求物体上升的高度CE (结果精确到 0.1m).
21.(8分)如图 1, AC是一段遥控车直线双车道跑道.甲、乙两遥控车分别从 A, B两处同时出发,7秒
后甲车先到达C点.设两车行驶时间为 x(秒 ),两车之间的距离为 y(米 ),根据图象解决下列问题:
(1)甲车经过 秒追上乙车, a .
(2)设相遇后两车之间的距离为 y1,求 y1与 x的
函数关系式.
(3)两遥控车出发后多长时间,它们之间的距离
为 4米?
第 3 页 共 4 页
22.(10分)综合与实践
【问题情境】
如图,在正方形 ABCD中,点 E在线段 AD上,点 F 在线段CD上,且始终满足 AE CF ,连接 BE ,BF ,
将线段 BE绕点 E逆时针旋转一定角度,得到线段 EG(点G是点 B旋转后的对应点),并使点G落在线段
BC上, EG与 BF 交于点H .
【初步分析】
(1)线段 EG与 BF的数量关系为 ,位置关系为 ;
【深入分析】
(2)如图②,再将线段 EG绕点 E逆时针旋转90 ,得到线段 EM(点M 是点G旋转后的对应点),连接 FM ,
请判断四边形 BEMF 的形状,并说明理由;
(3)如图③,若点G落在 BC的延长线上,且当点H 恰好为 EG的中点时,设CD与 EG交于点 N,AD 3,
求CG的长.
23.(10分)已知二次函数 y mx2 2mx 3,其中m 0.
(1)若二次函数经过 ( 1,4),求二次函数解析式.
(2)若该抛物线开口向上,当 1 x 2时,抛物线的最高点为M ,最低点为 N,点M 的纵坐标为 9,求
点M 和点 N的坐标.
(3)在二次函数图象上任取两点 (x1 , y1), (x2 , y2 ),当a x1 x2 a 2时,总有 y1 y2,求 a的取值范
围.
24.(12分)在 ABC内接于 O,点D在 O上,连结 AD,AO,分别交 BC于点 E,F , CAD BAO.
(1)求证: AD BC.
(2)若 AO / /CD.
①求证:CA CF .
②若CD 5, BF 10 ,求 BC的长.
第 4 页 共 4 页
参考答案与试题解析
一.选择题(共 10 小题)
题号 1 2 3 4 5 6 7 8 9 10
答案 D C C C B B C A D A
9 4a.解:抛物线对称轴为直线 x 2,当 x1 x 4时, x2a 2 2
2 2 x1,
则当 a 0时, y1 y2;当 a 0时, y1 y2 ;
当 x1 x2 4时, x2 2 2 x1,则当 a 0时, y2 y1;当 a 0时, y1 y2;
故 A、 B选项都不正确;
若 a(x1 x2 4) 0,则 a与 x1 x2 4同号,由上可知 y1 y2,故C不正确;
若 a(x1 x2 4) 0,则 a与 x1 x2 4异号,由上可知 y1 y2,故 D正确;
故选: D.
10.解:过点Q作QN AB于 N,连接Q、B、F ,则 QNE QNM 90 ,
EC EQ,CB CD, GBE CEQ BCD PCE A 90 ,
点Q、B、F 三点共线, QBN EBF 45 , EBF 、 BQN都是等腰直角三角形, QN BN ,
BCE BEC 90 , QEN BEC 90 , BCE QEN ,
ENQ CBE 90
在 ENQ和 CBE 中, QEN BCE , ENQ CBE (AAS ), EN CB,QN EB,
EQ CE
QN BN , EN CB 2EB, EB QN BN BG CG ,
设 EB QN BN BG CG a ,则 AB BC CD AD 2a, AN 2a a a,
DCP BCP 90 , BCE BCP 90 , DCP BCE,
CBE D 90
在 CBE 和 CDP中, CB CD , CBE CDP( ASA), BE DP a, PA 2a a a, PA QN,
BCE DCP
PMA QMN
在 PAM 和 QNM 中, , PAM QNM (AAS), AM MN 1 AN 1 a,BM 2a 1 a 3 A QNM 90 a,
2 2 2 2
PA QN
1 a 3 a
在Rt PAM中, tan APM tan AM 2 1 ,在Rt BCM BM 3中, tan BCM tan 2 ,
PA a 2 BC 2a 4
tan n tan 1 3 2, n , n ,故选: A.
2 4 3
第 5 页 共 4 页
二、填空题:(本大题共 6 小题,每小题 3 分,共 18 分)
11. a(a 4). 12.120 . 13.52 . 14.6. 15. 6 . 16.
15.解:如图所示,连接OB,OC, 圆心O到直线 l的距离OA 3, OA AB,
AB 3 tan ABO AO 3 , , BO AB2 AO2 2 3, ABO 30 ,
AB 3
将直线 l绕点 B逆时针旋转15 后得到的直线m, ABC 15 ,
CBO CBA ABO 45 ,
直线m恰好与 O相切于点C, OC BC, COB 45 , CB CO,CB2 CO2 BO2 ,
2CO2 (2 3)2 , CO 6 , O的半径为 6 .
16.解: 四边形 ABCD是平行四边形, AB / /CD,
将△ BCE沿 BE 翻折得△ BGE, CBE GBE, CEB AEB,CE GE,
设 CBE GBE , BG恰好平分 ABE , ABG GBE CBE , ABE 2 ,
AB / /CD, CEB ABE 2 , AEB ABE 2 , AE AB,
又 CE GE, AG AE GE AB CE 5 2 3;
如图所示,延长 BE交 AD的延长线于点 F ,过点 B分别作 AE, AF 的垂线,垂足分别为H ,M ,
AB AE, AEB ABE 2 , BAE 180 4 ,
BC / /AD,
F CBE , EAD BAD BAE (180 3 ) (180 4 ) ,
F EAF , EF EA 5,
DE CD EF DE 3 5 3 CE AB CE 5 2 3, AB / /DE, △ FED∽△ FBA, , ,
BF AB 5 BE 5
BF 25 BE BF EF 25 5 10 ,则 ,
3 3 3
在 Rt△ ABH ,Rt△ BEH 中,BE2 EH 2 AB2 AH 2 (10, )2 EH 2 52 (5 EH )2 EH 10,解得: ,
3 9
BH BE 2 HE 2 (10则 )2 (10 )2 20 2 ,GH GE EH 2 10 8 ,
3 9 9 9 9
Rt 20 2 8在 △ BGH 中, BG BH 2 GH 2 ( )2 ( )2 4 6 ,
9 9 3
5 20 2
BM HB
BGH C BAM , sin BGH sin BAM , , AB BH 9 25 3 ,
AB BG BM BG 4 6 9
3
第 6 页 共 4 页
25 6
在 Rt△ BMF 中,MF BF 2 BM 2 (5 10)2 (25 3)2 25 6
MF 6
, cos EAD cos F 9 25 ,3 9 9 BF 3
3
6
故答案为: .
3
三、解答题:(本大题有 8 小题,共 72 分)
2
17.解:(1 a 2 3 (a 1)(a 1))原式 1 2 9 4 12;(2)原式 a 1.
a 1 a 1
18.解:(1)此次调查的总人数为 9 15% 60(人 ),D项目的人数有 60 6 18 9 12 15(人 ),
补全条形统计图如下:
(2)图②中项目 E 12对应的圆心角的度数为 360 72 ;
60
故答案为:72;
18
(3)800 240(名 ),
60
答:估计本校七年级 800名学生中选择项目 B(乒乓球)的人数为 240名.
19.(1)证明: AB是直径, ADB 90 , AD BC, AB AC , BD CD;
(2)解: O与 AC相切, AB为直径, BA AC,
AB AC , BAC是等腰直角三角形, B 45 ;
(3)解:如图,作 ABC的角平分线交 AD于点 E,则点 E即是劣弧 AD的中点.
20.解:(1)由题意得: BCA 90 ,
AC AC 3 1 3m, CAB 60 ,在 Rt△ ABC中,由 cos A ,得 cos60 , AB 6m;
AB AB 2
(2)在 Rt△ ABC中,由勾股定理得: BC AB2 AC 2 3 3(m),在 Rt△ BCD中, sin CDB BC ,
BD
sin37 3 3 0.6, BD 5 3m,由题意得, BC AB BE BD,
BD
BE BC AB BD 3 3 6 5 3 6 2 3(m) , CE BC BE 3 3 (6 2 3) 5 3 6 2.7(m) ,
答:物体上升的高度约为 2.7m.
21.解:(1)由图象可知,甲车经过 3秒追上乙车;
甲的速度比乙的速度快 6 3 2(米 /秒),则 7秒时甲、乙之间的距离为 2 (7 3) 8(米 ), a 8.
故答案为:3,8.
(2) y1 2(x 3) 2x 6, y1与 x的函数关系式为 y1 2x 6.
(3)当0 x 3时,当之间的距离为 4米时,得 6 2x 4,解得 x 1;
第 7 页 共 4 页
当3 x 7时,当之间的距离为 4米时,得 2x 6 4,解得 x 5.
答:两遥控车出发后 1秒或 5秒时,它们之间的距离为 4米.
22.解:(1) EG BF, EG BF ;理由如下:
四边形 ABCD是正方形 A C ABC 90 , AB CB,
又 AE CF, ABE CBF (SAS ), BE BF , ABE CBF .
由旋转的性质,得 BE EG, EG BF , EBG EGB.
又 ABE EBG ABC 90 , CBF EGB 90 , BHG 90 ,即 EG BF .
故答案为: EG BF, EG BF ;
(2)四边形 BEMF 为菱形,理由如下:
由旋转的性质,得 EG EM , GEM 90 ,
又 EG BF , BHE 90 , EM BF, GEM BHE 90 , EM / /BF , 四边形 BEMF 是平行四边形,
又 BE BF , 四边形 BEMF 是菱形;
(3) 点H 是 EG的中点, BF EG, BF是 EG的垂直平分线, BE BG, EBF GBF .
ABE CBF ABE CBF EBF 1 1又 , ABC 90 30 .
3 3
四边形 ABCD是正方形, D 90 ,AB AD CD BC 3, 在Rt ABE中,BE AB 3 2 3,
sin 60 3
2
BG 2 3, CG BG BC 2 3 3.
23.解:(1)把 ( 1,4) 1 1 2代入函数解析式得m 2m 3 4, m , 函数解析式为: y x2 x 3;
3 3 3
(2) 抛物线开口方向向上, m 0,
y mx2 2mx 3 m(x 1)2 3 m, 抛物线的顶点为 (1,3 m),
当 x 1时 y随 x增大而减小,当 x 1时, y随 x增大而增大, 最低点 N (1,3 m),
当 x 1时, y 3m 3,当 x 2时, y 3,且m 0, 3m 3 3, 最高点M ( 1,3m 3),
3m 3 9, m 2,代入M 点和 N点坐标得:M ( 1,9), N (1,1);
(3)①当m 0时,
则有当 x 1时 y随 x增大而减小,当 x 1时, y随 x增大而增大,
又 当a x1 x2 a 2时,总有 y1 y2,此时 a 2 1,
a 1,
第 8 页 共 4 页
②当m 0时,
则有当 x 1时 y随 x增大而增大,当 x 1时, y随 x增大而减小,
又 当a x1 x2 a 2时,总有 y1 y2,此时 a 1,
综上,当m 0时 a 1;当m 0时, a 1.
24.(1)证明:延长 AO交 O于点M ,连结CM ,如图,
AM 为 O的直径, ACM 90 , BCM ACE 90 ,
BCM BAO, BAO ACE 90 ,
CAD BAO, CAD ACE 90 ,即 AEC 90 , AD BC;
(2)①证明: AO / /CD, FAE D,
D B, FAE B,
CAF CAE FAE, FAB B AFC,又 CAD BAO,即 CAE FAB,
CAF AFC, CA CF ;
②解: CAD FAB, D B ACD AC CD 5, ∽ AFB, ,
AF BF 10
设 AC 5a,则 AF 10a,由①知CF CA, CF 5a,
设CE x,则 EF 5a x,由(1)知 AD BC, AE 2 AC 2 CE 2 , AE2 AF 2 EF 2,
AC 2 CE 2 AF 2 EF 2 , (5a)2 x2 ( 10a)2 (5a x)2 , x 4a,即CE 4a, EF a,
AE AC2 CE2 (5a)2 (4a)2 3a,
FAE AE EF B, AEF BEA, AEF∽ BEA, ,即 AE2 EF EB,
EB AE
(3a)2 a (a 10) 10 5 10 5 10 13 10 ,解得 a , CF 5a , BC CF BF 10 .
8 8 8 8
第 9 页 共 4 页
同课章节目录
