期中真题专项复习01 选择题(含答案)--2024-2025学年八年级数学下册(冀教版)
文档属性
| 名称 | 期中真题专项复习01 选择题(含答案)--2024-2025学年八年级数学下册(冀教版) |  | |
| 格式 | docx | ||
| 文件大小 | 501.4KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-03-30 11:31:29 | ||
图片预览




文档简介
2024-2025学年八年级数学下册(冀教版)
期中真题专项复习01 选择题
一、选择题
1.(2024八下·唐山期中)如图,在平行四边形ABCD中,E、F、G、H分别是各边的中点,在下列四个图形中,阴影部分的面积与其他三个阴影部分面积不相等的是( )
A. B.
C. D.
2.(2024八下·遵化期中)在平面直角坐标系中,点在( )
A.轴的负半轴上 B.轴的负半轴上
C.轴的正半轴上 D.轴的正半轴上
3.(2024八下·丛台期中)下列选项中y不是x的函数的是( )
A. B.
C. D.
4.(2024八下·丛台期中)如图.P是面积为S的平行四边形ABCD内任意一点,△PAD的面积为,△PBC的面积为,则( )
A. B.
C. D.的大小与P点位置有关
5.(2024八下·承德期中)如图,在中,对角线,相交于点,添加下列条件不能判定是菱形的只有( )
A. B. C. D.
6.(2024八下·承德期中)如图,矩形的对角线、相交于点O,分别过点C、D作、的平行线相交于点E.若,则点E到的距离是( )
A.7 B.8 C.9 D.12
7.(2024八下·卢龙期中)在频数分布直方图中,各个小组的频数比为1:5:4:6,则对应的小长方形的高的比为( )
A.1:4:5:3 B.1:5:3:6 C.1:5:4:6 D.6:4:5:1
8.(2024八下·承德期中)如图,矩形的对角线与相交于点O,,则的值为( )
A.5 B.4 C.3.5 D.3
9.(2024八下·威县期中)如图,菱形的对角线相交于点为上的点,顺次连接四点,所得四边形恰好是正方形.若,,则菱形的面积为( )
A.2 B.4 C.6 D.8
10.(2024八下·桥西期中)在平面直角坐标系中,点向下平移5个单位长度后,得到对应点的坐标为( )
A. B. C. D.
11.(2024八下·海口期中)如图,已知平行四边形中,,则( )
A.18° B.36° C.72° D.144°
12.(2024八下·承德期中)如图,在菱形中,E、F分别是、的中点,如果,那么菱形的周长是( )
A.8 B.12 C.14 D.16
13.(2024八下·汕头期中)两条对角线相等且互相垂直平分的四边形是( )
A.平行四边形 B.矩形
C.菱形 D.正方形
14.(2021八下·丰南期中)如图是我国古代著名的“赵爽弦图”的示意图,此图是由四个全等的直角三角形拼接而成,其中AE=10,BE=24,则EF的长是( )
A.14 B.16 C.14 D.14
15.(2024八下·遵化期中)要反应我区2019年12月份每天的最高气温的变化情况,宜采用( )
A.条形统计图 B.扇形统计图 C.折线统计图 D.统计表
16.(2023八下·秦皇岛期中)为了观察某一段时间内温度的变化,记录了每天固定时刻的温度,根据这些数据制成统计图,选取的最佳统计图是( )
A.条形统计图 B.扇形统计图 C.折线统计图 D.都可以
17.(2024八下·丰润期中) 如图,在矩形ABCD 中,对角线AC与BD相交于点 O,添加下列条件不能判定矩形 ABCD 是正方形的是 ( )
A.AB=BC B.AC=BD C.AC⊥BD D.∠1=∠2
18.(2024八下·遵化期中)用下列方式获取的数据中,可信度较低的是( )
A.社会上的传闻 B.从报纸上摘录的
C.看电视新闻得到的 D.小组实地考察或测量得到的
19.(2024八下·赵县期中)如图,在□ABCD中,ABAC,若AB=4,AC=6,则BD的长是( )
A.11 B.10 C.9 D.8
20.(2023八下·新兴期中) 四边形 中,对角线与交于点O,下列条件中不一定能判定这个四边形是平行四边形的是( )
A., B.,
C., D.,
21.(2024八下·石家庄期中)如图,红旗中学七年级(6)班就上学方式作出调查后绘制了条形图,那么乘车上学的同学人数占全班人数的( )
A. B. C. D.
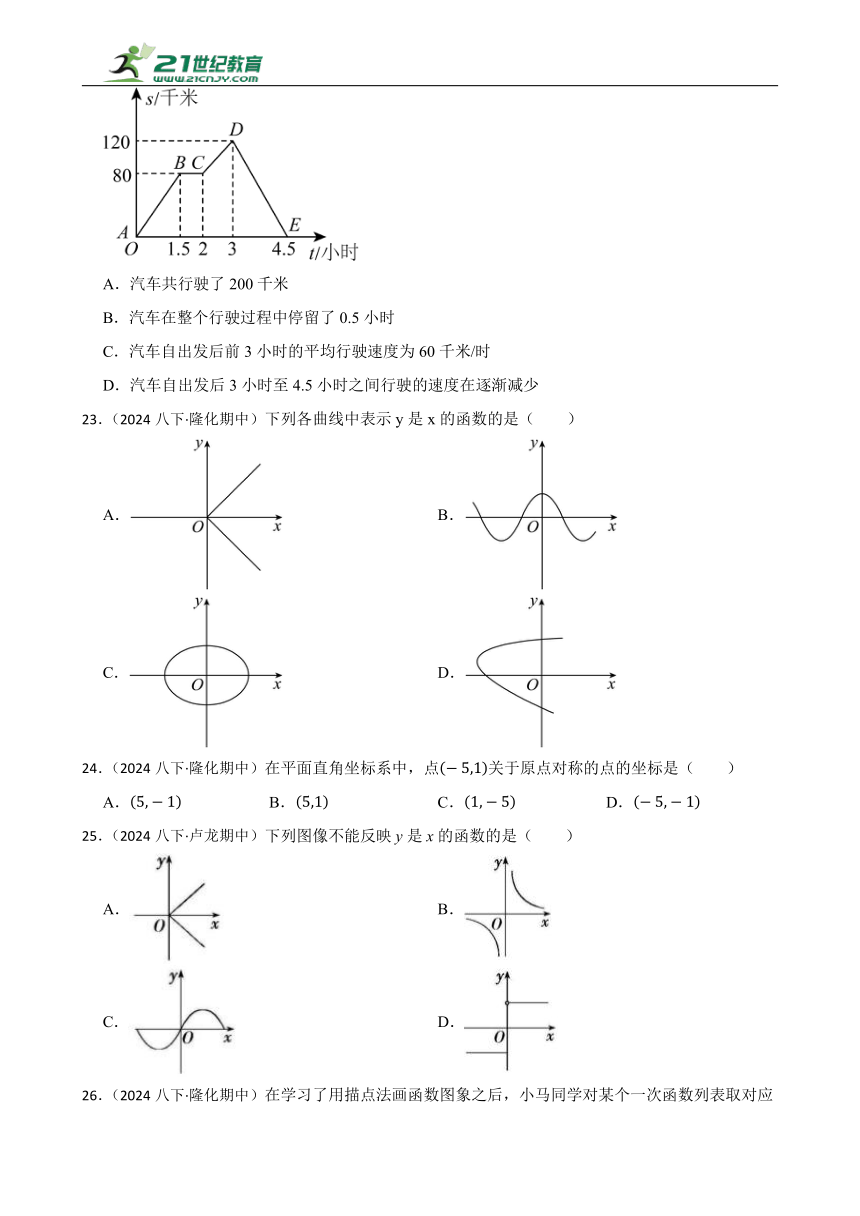
22.(2024八下·隆化期中)如图,折线描述了一辆能源汽车在某一直线公路上的行驶过程中,汽车离出发地的距离(千米)和行驶时间(小时)之间的函数关系根据图中提供的信息,给出下列说法,其中正确的说法是( )
A.汽车共行驶了200千米
B.汽车在整个行驶过程中停留了0.5小时
C.汽车自出发后前3小时的平均行驶速度为60千米/时
D.汽车自出发后3小时至4.5小时之间行驶的速度在逐渐减少
23.(2024八下·隆化期中)下列各曲线中表示y是x的函数的是( )
A. B.
C. D.
24.(2024八下·隆化期中)在平面直角坐标系中,点关于原点对称的点的坐标是( )
A. B. C. D.
25.(2024八下·卢龙期中)下列图像不能反映y是x的函数的是( )
A. B.
C. D.
26.(2024八下·隆化期中)在学习了用描点法画函数图象之后,小马同学对某个一次函数列表取对应值如表:
… 0 1 2 …
… 0 3 …
他在最后描点连线时发现有一个点明显不对,这个点是( )
A. B. C. D.
27.(2024八下·遵化期中)已知点在正比例函数的图象上,则的值是( )
A. B. C.6 D.
28.(2024八下·平山期中)综合实践课上,嘉嘉画出,利用尺规作图找一点C,使得四边形为平行四边形.图1~图3是其作图过程.
(1)作的垂直平分线交于点O; (2)连接,在的延长线上截取; (3)连接,,则四边形即为所求.
在嘉嘉的作法中,可直接判定四边形ABCD为平行四边形的条件是( )
A.两组对边分别平行 B.两组对边分别相等
C.对角线互相平分 D.一组对边平行且相等
29.(2024八下·雄安期中)如图1,中,,为锐角.要在对角线BD上找点N,M,使四边形ANCM为平行四边形,现有图2中的甲、乙、丙三种方案,则正确的方案( ).
取BD中点O,作, 作于N,于M 作AN,CM分别平分,,交BD于点N,M
A.甲、乙、丙都是 B.只有甲、乙才是
C.只有甲、丙才是 D.只有乙、丙才是
30.(2024八下·遵化期中)在平面直角坐标系中,一次函数的图像与轴的交点坐标为( )
A. B. C. D.
31.(2024八下·宣化期中)如图,在 中,以为圆心,任意长为半径画弧,分别交,于点,,分别以,为圆心,以大于为半径画弧,两弧交于点作射线交于点,若,则( )
A. B. C. D.
32.(2024八下·卢龙期中)以下调查中,最适合用来全面调查的是( )
A.了解班级每位同学穿鞋的尺码 B.了解中学生的心理健康状况
C.调查滦河水质情况 D.了解市民做高铁出行的意愿
33.(2024八下·卢龙期中)已知甲、乙、丙三人所处位置不同.甲说:“以我为坐标原点,乙的位置是.”丙说:“以我为坐标原点,乙的位置是.”若以乙为坐标原点(三人建立平面直角坐标系时,x轴、y轴正方向分别相同),甲、丙的坐标分别是( )
A., B.,
C., D.,
34.(2024八下·石家庄期中)关于一次函数,下列说法正确的是( )
A.图象经过点
B.图象向上平移1个单位长度后得到的函数解析式为
C.图象不经过第二象限
D.若两点,在该函数图象上,则
35.(2024八下·承德期中)我国古代数学家赵爽的“勾股圆方图”是由四个全等的直角三角形与中间的一个小正方形拼成一个大正方形(如图所示).如果大正方形的面积是13,小正方形的面积是1,直角三角形的两直角边长分别为,那么的值是( )
A.20 B.12 C.24 D.25
36.(2024八下·商水期中)如图,在中,,平分,平分,则长为( )
A.2 B.3 C.4 D.5
37.(2024八下·镇海区期中)下列多边形中,内角和等于外角和的是( )
A. B.
C. D.
38.(2022八下·阜平期中)如图,矩形中,,在数轴上,若以点A为圆心,对角线的长为半径作弧交数轴于点M,则点M表示的数为( )
A.2 B. C. D.
39.(2024八下·巴楚期中)如图,在平行四边形ABCD中,∠B+∠D=100°,则∠A等于( )
A.50° B.100° C.130° D.150°
40.(2024八下·卢龙期中)在平面直角坐标系中,一矩形上各点的纵坐标不变,横坐标变为原来的,则该矩形发生的变化为( )
A.向左平移了二个单位长度 B.向下平移了二个单位长度
C.横向压缩为原来的一半 D.纵向压缩为原来的一半
41.(2024八下·凤鸣期中)某洗衣机在洗涤衣服时经历了注水、清洗、排水三个连续过程(工作前洗衣机内无水),在这三个过程中洗衣机内水量y(升)与时间x(分)之间的函数关系对应的图象大致为( )
A. B.
C. D.
42.(2024八下·遵化期中)某汽车油箱中盛有油,装满货物行驶的过程中每小时耗油8L,则油箱中的剩油量与时间之间的关系式是( )
A. B. C. D.
43.(2024八下·杭州期中)如图,四边形ABCD是平行四边形,O是对角线AC与BD的交点,AB⊥AC,若AB=8,AC=12,则BD的长是( )
A.16 B.18 C.20 D.22
44.(2024八下·遵化期中)下列数据不能确定物体具体位置的是( )
A.5楼6号 B.北偏东
C.希望路20号 D.东经,北纬
45.(2024八下·临湘期中)如图,依次连接第一个矩形各边的中点得到一个菱形,再依次连接菱形各边的中点得到第二个矩形,按照此方法继续下去.已知第一个矩形的面积为1,则第n个矩形的面积为( )
A. B. C. D.
46.(2024八下·隆化期中)为了解某学校4000名学生课外阅读情况,随机抽取400名学生进行调查,下列说法错误的是( )
A.400名学生是样本容量
B.400名学生课外读书情况是一个样本
C.每名学生的课外读书情况是个体
D.4000名学生课外读书情况是总体
47.(2024八下·扶沟期中)如图,在平行四边形ABCD中,AB=4,∠BAD的平分线与BC的延长线交于点E,与DC交于点F,且点F为边DC的中点,DG⊥AE,垂足为G,若DG=1,则AE的边长为( )
A. B. C.4 D.8
48.(2024八下·卢龙期中)向最大容量为60升的热水器内注水,每分钟注水10升,注水2分钟后停止1分钟,然后继续注水,直至注满.则能反映注水量与注水时间函数关系的图象是 ( )
A. B.
C. D.
49.(2024八下·新乡期中)如图,E,F分别是平行四边形的边,上的点,与相交于点P,与相交于点Q,若,,,则阴影部分的面积为( )
A. B. C. D.
50.(2024八下·宣化期中)如图,在平行四边形中,对角线,相交于点O,过点O,交于点F,交于点E.若,,,则图中阴影部分的面积是( )
A.1.5 B.3 C.6 D.4
答案解析部分
1.B
2.B
解:点,横坐标为0,纵坐标为,则该点在轴负半轴上,
故答案为:B.
本题考查平面直角坐标系点的位置特征.先判断点横坐标和纵坐标的特征,再根据平面直角坐标系中点的特征进行判断可选出答案.
3.A
解:A y不是x的函数,故A项符合题意;
B y是x的函数,故B项不符合题意;
C y是x的函数,故C项不符合题意;
D y=5-y,y是x的函数,故D项不符合题意.
故答案为:A.
根据函数的定义可知,对于每一个确定的x的值,y都有唯一确定的值与其对应,即可判断.
4.C
解:过点P作直线l使AD⊥l,分别交AD,BC于点M,N,如图,
则MN⊥AD,
∵ 四边形ABCD为平行四边形,
∴ MN⊥BC,
∴ S=,
S1=,
S2=,
∴ .
故答案为:C.
过点P作直线l使AD⊥l,分别交AD,BC于点M,N,根据平行四边形的性质可得MN⊥BC,根据平行四边形的面积公式和三角形的面积公式,即可求得.
5.C
6.C
7.C
解:∵在频数分布直方图中各小长方形的高的比等于频数之比,
∴各个小组的频数比为,则对应的小长方形的高的比为.
故答案为C.
本题考查频数分布直方图的特点.根据频数分布直方图中各小长方形的高的比等于频数之比,据此可选出答案.
8.B
9.B
10.A
解:由题意得点向下平移5个单位长度即纵坐标-5,
∴平移后得到对应点的坐标为,
故答案为:A
根据坐标与图形的变化-平移结合题意即可求解。
11.B
12.D
13.D
解:根据正方形的判别方法知,两条对角线互相垂直平分的四边形是菱形,且相等又可判定为正方形,故选D.
两条对角线互相垂直平分的四边形是菱形,对角线相等的菱形是正方形,所以该四边形是正方形.
14.D
解:∵AE=10,BE=24,即24和10为两条直角边长时,
小正方形的边长=24-10=14,
∴EF=.
故答案为:D.
先求出小正方形的边长,再利用勾股定理求出EF的长即可。
15.C
解:要反映每天的气温升高、降低的变化情况,因此选择折线统计图较好,
故答案为:C.
本题考查统计图的选择.根据题意:要反映经开区年月份每天的最高气温的变化情况,因此符合折线统计图的特点,因此选择折线统计图比较合适.
16.C
解:
∵观察某一段时间内温度的变化,
∴适合选取折线统计图,
故答案为:C
根据每种统计图的特点进行选取即可求解。
17.B
解:A、邻边相等的矩形是正方形,A不符合题意;
B、矩形的对角线相等,但对角线相等的矩形不一定是正方形,B符合题意;
C、∵四边形是矩形,
∴,,
∵,
∴,
∴矩形为正方形,C不符合题意;
D、∵,,
∴,
∴,
∴,
∴矩形是正方形,D不符合题意
故答案为:B
根据正方形的判定与性质,矩形的判定与性质结合题意添加条件即可求解。
18.A
解:A、社会上的传闻很多是人们道听途说的,可信度比较低,故本选项符合题意,A正确;
B、从报纸上摘录的信息,因为报纸是国家正规报纸,所以可信度很高,故本选项不合题意,B错误;
C、电视上的新闻报道的大都是事实事件,所以可信度很高,故本选项不合题意,C错误;
D、考察或测量得到的可信度很高,故本选项不合题意,D错误.
故答案为:A.
本题考查调查收集数据的过程与方法.根据传闻可信度比较低可判断A选项;根据报纸可信度很高,据此可判断B选项;根据电视上的新闻报道可信度很高可判断C选项;根据考察或测量可信度很高据此可判断D选项.
19.B
20.A
21.B
22.B
23.B
24.A
25.A
解:A、当x取一值时,y没有唯一与它对应的值,y不是x的函数,故答案为项A符合题意,A错误;
B、当x取一值时,y有唯一与它对应的值,y是x的函数,故答案为项B不合题意,B错误;
C、当x取一值时,y有唯一与它对应的值,y是x的函数,故答案为项C不合题意,C错误;
D、当x取一值时,y有唯一与它对应的值,y是x的函数,故答案为项D不合题意,D错误;
故答案为A.
本题考查函数的概念.根据函数的概念:当x取一值时,y有唯一与它对应的值.进行逐项判断可选出答案.
26.C
27.A
解:把点代入正比例函数解析式中,
得,
解得,
故答案为A.
本题考查图象过点问题.把点代入正比例函数解析式中,通过化简可求出的值.
28.C
29.A
30.D
解:令x=0, ,
∴一次函数的图象与轴的交点的坐标为.
故答案为:D
本题考查一次函数的图象和性质.令x=0,可求出函数值,据此可求出图象与轴的交点的坐标.
31.C
解:由作图得:平分,
∴,
在中,,,,
∴,
∴,
∴,
∴,
故答案为:.
根据角平分线定义可得,再根据平行四边形性质可得,,,则,即,根据等角对等边可得,再根据边之间的关系即可求出答案.
32.A
解:A、了解班级每位同学穿鞋的尺码,适合全面调查,选项说法正确,符合题意,A正确;
B、了解中学生的心理健康状况,适合抽样调查,选项说法错误,不符合题意,B错误;
C、调查长江水质情况,适合抽样调查,选项说法错误,不符合题意,C错误;
D、了解市民做高铁出行的意愿,适合抽样调查,选项说法错误,不符合题意,D错误;
故答案为:A.
本题考查全面调查和抽样调查的定义.根据全面调查的定义: 是对需要调查的对象逐个调查; 抽样调查的定义: 在被调查对象的总体中,抽取若干个体作为样本进行调查,然后根据对样本的调查结果来推导总体的一般特征; ,逐项进行判断可选出答案.
33.C
解:以甲为坐标原点,乙的位置是(2,3),则以乙为坐标原点,甲的位置是(-2,-3);
以丙为坐标原点,乙的位置是(-3,-2),则以乙为坐标原点,丙的位置是(3,2).
故答案为:C.
本题考查坐标确定位置.由于已知三人建立坐标系时,x轴y轴正方向相同,根据:直角坐标平面内点的位置由有序实数对确定,有序实数对与点一一对应,则以甲为坐标原点,乙的位置是(2,3),则以乙为坐标原点,甲的位置是(-2,-3);同样得到以丙为坐标原点,乙的位置是(-3,-2),则以乙为坐标原点,丙的位置是(3,2).
34.D
解:A、当x=2时,y=-2+6=4≠1,A错误;
B、图象向上平移1个单位长度后得到的函数解析式为,B错误;
C、k=-1<0,b=6>0,
其图像经过第一、二、四象限,C错误;
D、k=-1<0,
y随x的增大而减小,
1>-1,
,D正确.
故答案为:D.
把x=2代入表达式求出y的值即可判断A;根据平移的性质为上加下减即可判断B;由k=-1<0,b=6>0,得出一次函数所经过的象限即可判断C;由k<0,得到y随x的增大而减小即可判断D.
35.D
36.A
解:∵,
∴.
∴.
∵平分,
∴.
∴.
∴.
同理可得.
∴.
故答案为:A.
根据平行四边形性质可得,则,再根据角平分线定义可得,则,再根据等角对等边可得,同理可得,再根据边之间的关系即可求出答案.
37.B
解:任意多边形的外角和等于360°,
A、三角形的内角和等于180°,180°不等于360°,不符合题意;
B、四边形的内角和等于360°,360°等于360°,符合题意;
C、五边形的内角和等于540°,540°不等于360°,不符合题意;
D、六边形的内角和等于720°,720°不等于360°,不符合题意.
故答案为:B.
根据任意多边形的外角和等于360°,要使内角和等于外角和,利用公式求出多边形内角和即可判断.
38.C
39.C
解:∵四边形ABCD是平行四边形,
∴∠B=∠D,∠A+∠B=180°,
∵∠B+∠D=100°,
∴∠B=∠D=50°,
∴∠A=130°,
故答案为:C.
由四边形ABCD是平行四边形,得出∠A+∠B=180°,即可求解∠B的度数,再利用平行四边形的邻角互补求得答案即可。
40.C
解:先设矩形中某个点的坐标为,则由一矩形上各点的纵坐标不变,横坐标变为原来的,可知该点的坐标变为,
∴该矩形发生的变化为横向压缩原来的一半;
故答案为C.
本题考查平面直角坐标系点的坐标特征及矩形的性质.先设矩形中某个点的坐标为,根据矩形的性质、平移的性质可求出该点的坐标变为,据此可找出矩形发生的变化,选出答案.
41.D
解:∵洗衣机工作前洗衣机内无水,
∴A,B两选项不正确,被淘汰;
又∵洗衣机最后排完水,
∴C选项不正确,被淘汰,
所以选项D正确.
故选:D.
根据洗衣机内水量开始为0,清洗时水量不变,排水时水量变小,直到水量0,即可得到答案.
42.C
解:根据题意,得,
故,
故答案为C.
本题考查了一次函数的应用.根据耗油量+剩油量=100,据此可列出式子,再进行变形可得到答案.
43.C
解:∵四边形ABCD是平行四边形,AC=12,
∴OA=AC=6,BD=2OB,
∵AB⊥AC,AB=8,
∴OB==10,
∴BD=2OB=20.
故选C.
由四边形ABCD是平行四边形,根据平行四边形的对角线互相平分,可得OA的长,然后由AB⊥AC,AB=8,AC=12,根据勾股定理可求得OB的长,继而求得答案.
44.B
解:5楼6号、希望路20号、东经,北纬都能确定物体的具体位置,
北偏东不能确定物体的具体位置,
故答案为:B.
本题考查坐标确定位置.根据坐标确定位置.:一对有序实数对才能确定一个点的位置.在平面直角坐标系中,要用两个数据才能表示一个点的位置.北偏东只有一个数据,故不能确定一个位置.
45.D
解:已知第一个矩形的面积为1;
第二个矩形的面积为原来的()2×2-2=;
第三个矩形的面积是()2×3-2=;
…
故第n个矩形的面积为:= .
故答案为:D.
先求出第二个矩形的面积为,第三个矩形的面积是,依次类推,可得第n个矩形的面积为,即可判断.
46.A
47.B
48.D
解:注水需要60÷10=6分钟,注水2分钟后停止注水1分钟,共经历6+1=7分钟,排除A、B;再根据停1分钟,再注水4分钟,排除C.
故答案为:D.
先计算出注水所需的时间,即60÷10=6分钟,由于中途休息了1分钟,则共需要7分钟,由题意得2到3分钟之间休息,则2到3分钟之间线段与x轴平行.
49.B
50.C
期中真题专项复习01 选择题
一、选择题
1.(2024八下·唐山期中)如图,在平行四边形ABCD中,E、F、G、H分别是各边的中点,在下列四个图形中,阴影部分的面积与其他三个阴影部分面积不相等的是( )
A. B.
C. D.
2.(2024八下·遵化期中)在平面直角坐标系中,点在( )
A.轴的负半轴上 B.轴的负半轴上
C.轴的正半轴上 D.轴的正半轴上
3.(2024八下·丛台期中)下列选项中y不是x的函数的是( )
A. B.
C. D.
4.(2024八下·丛台期中)如图.P是面积为S的平行四边形ABCD内任意一点,△PAD的面积为,△PBC的面积为,则( )
A. B.
C. D.的大小与P点位置有关
5.(2024八下·承德期中)如图,在中,对角线,相交于点,添加下列条件不能判定是菱形的只有( )
A. B. C. D.
6.(2024八下·承德期中)如图,矩形的对角线、相交于点O,分别过点C、D作、的平行线相交于点E.若,则点E到的距离是( )
A.7 B.8 C.9 D.12
7.(2024八下·卢龙期中)在频数分布直方图中,各个小组的频数比为1:5:4:6,则对应的小长方形的高的比为( )
A.1:4:5:3 B.1:5:3:6 C.1:5:4:6 D.6:4:5:1
8.(2024八下·承德期中)如图,矩形的对角线与相交于点O,,则的值为( )
A.5 B.4 C.3.5 D.3
9.(2024八下·威县期中)如图,菱形的对角线相交于点为上的点,顺次连接四点,所得四边形恰好是正方形.若,,则菱形的面积为( )
A.2 B.4 C.6 D.8
10.(2024八下·桥西期中)在平面直角坐标系中,点向下平移5个单位长度后,得到对应点的坐标为( )
A. B. C. D.
11.(2024八下·海口期中)如图,已知平行四边形中,,则( )
A.18° B.36° C.72° D.144°
12.(2024八下·承德期中)如图,在菱形中,E、F分别是、的中点,如果,那么菱形的周长是( )
A.8 B.12 C.14 D.16
13.(2024八下·汕头期中)两条对角线相等且互相垂直平分的四边形是( )
A.平行四边形 B.矩形
C.菱形 D.正方形
14.(2021八下·丰南期中)如图是我国古代著名的“赵爽弦图”的示意图,此图是由四个全等的直角三角形拼接而成,其中AE=10,BE=24,则EF的长是( )
A.14 B.16 C.14 D.14
15.(2024八下·遵化期中)要反应我区2019年12月份每天的最高气温的变化情况,宜采用( )
A.条形统计图 B.扇形统计图 C.折线统计图 D.统计表
16.(2023八下·秦皇岛期中)为了观察某一段时间内温度的变化,记录了每天固定时刻的温度,根据这些数据制成统计图,选取的最佳统计图是( )
A.条形统计图 B.扇形统计图 C.折线统计图 D.都可以
17.(2024八下·丰润期中) 如图,在矩形ABCD 中,对角线AC与BD相交于点 O,添加下列条件不能判定矩形 ABCD 是正方形的是 ( )
A.AB=BC B.AC=BD C.AC⊥BD D.∠1=∠2
18.(2024八下·遵化期中)用下列方式获取的数据中,可信度较低的是( )
A.社会上的传闻 B.从报纸上摘录的
C.看电视新闻得到的 D.小组实地考察或测量得到的
19.(2024八下·赵县期中)如图,在□ABCD中,ABAC,若AB=4,AC=6,则BD的长是( )
A.11 B.10 C.9 D.8
20.(2023八下·新兴期中) 四边形 中,对角线与交于点O,下列条件中不一定能判定这个四边形是平行四边形的是( )
A., B.,
C., D.,
21.(2024八下·石家庄期中)如图,红旗中学七年级(6)班就上学方式作出调查后绘制了条形图,那么乘车上学的同学人数占全班人数的( )
A. B. C. D.
22.(2024八下·隆化期中)如图,折线描述了一辆能源汽车在某一直线公路上的行驶过程中,汽车离出发地的距离(千米)和行驶时间(小时)之间的函数关系根据图中提供的信息,给出下列说法,其中正确的说法是( )
A.汽车共行驶了200千米
B.汽车在整个行驶过程中停留了0.5小时
C.汽车自出发后前3小时的平均行驶速度为60千米/时
D.汽车自出发后3小时至4.5小时之间行驶的速度在逐渐减少
23.(2024八下·隆化期中)下列各曲线中表示y是x的函数的是( )
A. B.
C. D.
24.(2024八下·隆化期中)在平面直角坐标系中,点关于原点对称的点的坐标是( )
A. B. C. D.
25.(2024八下·卢龙期中)下列图像不能反映y是x的函数的是( )
A. B.
C. D.
26.(2024八下·隆化期中)在学习了用描点法画函数图象之后,小马同学对某个一次函数列表取对应值如表:
… 0 1 2 …
… 0 3 …
他在最后描点连线时发现有一个点明显不对,这个点是( )
A. B. C. D.
27.(2024八下·遵化期中)已知点在正比例函数的图象上,则的值是( )
A. B. C.6 D.
28.(2024八下·平山期中)综合实践课上,嘉嘉画出,利用尺规作图找一点C,使得四边形为平行四边形.图1~图3是其作图过程.
(1)作的垂直平分线交于点O; (2)连接,在的延长线上截取; (3)连接,,则四边形即为所求.
在嘉嘉的作法中,可直接判定四边形ABCD为平行四边形的条件是( )
A.两组对边分别平行 B.两组对边分别相等
C.对角线互相平分 D.一组对边平行且相等
29.(2024八下·雄安期中)如图1,中,,为锐角.要在对角线BD上找点N,M,使四边形ANCM为平行四边形,现有图2中的甲、乙、丙三种方案,则正确的方案( ).
取BD中点O,作, 作于N,于M 作AN,CM分别平分,,交BD于点N,M
A.甲、乙、丙都是 B.只有甲、乙才是
C.只有甲、丙才是 D.只有乙、丙才是
30.(2024八下·遵化期中)在平面直角坐标系中,一次函数的图像与轴的交点坐标为( )
A. B. C. D.
31.(2024八下·宣化期中)如图,在 中,以为圆心,任意长为半径画弧,分别交,于点,,分别以,为圆心,以大于为半径画弧,两弧交于点作射线交于点,若,则( )
A. B. C. D.
32.(2024八下·卢龙期中)以下调查中,最适合用来全面调查的是( )
A.了解班级每位同学穿鞋的尺码 B.了解中学生的心理健康状况
C.调查滦河水质情况 D.了解市民做高铁出行的意愿
33.(2024八下·卢龙期中)已知甲、乙、丙三人所处位置不同.甲说:“以我为坐标原点,乙的位置是.”丙说:“以我为坐标原点,乙的位置是.”若以乙为坐标原点(三人建立平面直角坐标系时,x轴、y轴正方向分别相同),甲、丙的坐标分别是( )
A., B.,
C., D.,
34.(2024八下·石家庄期中)关于一次函数,下列说法正确的是( )
A.图象经过点
B.图象向上平移1个单位长度后得到的函数解析式为
C.图象不经过第二象限
D.若两点,在该函数图象上,则
35.(2024八下·承德期中)我国古代数学家赵爽的“勾股圆方图”是由四个全等的直角三角形与中间的一个小正方形拼成一个大正方形(如图所示).如果大正方形的面积是13,小正方形的面积是1,直角三角形的两直角边长分别为,那么的值是( )
A.20 B.12 C.24 D.25
36.(2024八下·商水期中)如图,在中,,平分,平分,则长为( )
A.2 B.3 C.4 D.5
37.(2024八下·镇海区期中)下列多边形中,内角和等于外角和的是( )
A. B.
C. D.
38.(2022八下·阜平期中)如图,矩形中,,在数轴上,若以点A为圆心,对角线的长为半径作弧交数轴于点M,则点M表示的数为( )
A.2 B. C. D.
39.(2024八下·巴楚期中)如图,在平行四边形ABCD中,∠B+∠D=100°,则∠A等于( )
A.50° B.100° C.130° D.150°
40.(2024八下·卢龙期中)在平面直角坐标系中,一矩形上各点的纵坐标不变,横坐标变为原来的,则该矩形发生的变化为( )
A.向左平移了二个单位长度 B.向下平移了二个单位长度
C.横向压缩为原来的一半 D.纵向压缩为原来的一半
41.(2024八下·凤鸣期中)某洗衣机在洗涤衣服时经历了注水、清洗、排水三个连续过程(工作前洗衣机内无水),在这三个过程中洗衣机内水量y(升)与时间x(分)之间的函数关系对应的图象大致为( )
A. B.
C. D.
42.(2024八下·遵化期中)某汽车油箱中盛有油,装满货物行驶的过程中每小时耗油8L,则油箱中的剩油量与时间之间的关系式是( )
A. B. C. D.
43.(2024八下·杭州期中)如图,四边形ABCD是平行四边形,O是对角线AC与BD的交点,AB⊥AC,若AB=8,AC=12,则BD的长是( )
A.16 B.18 C.20 D.22
44.(2024八下·遵化期中)下列数据不能确定物体具体位置的是( )
A.5楼6号 B.北偏东
C.希望路20号 D.东经,北纬
45.(2024八下·临湘期中)如图,依次连接第一个矩形各边的中点得到一个菱形,再依次连接菱形各边的中点得到第二个矩形,按照此方法继续下去.已知第一个矩形的面积为1,则第n个矩形的面积为( )
A. B. C. D.
46.(2024八下·隆化期中)为了解某学校4000名学生课外阅读情况,随机抽取400名学生进行调查,下列说法错误的是( )
A.400名学生是样本容量
B.400名学生课外读书情况是一个样本
C.每名学生的课外读书情况是个体
D.4000名学生课外读书情况是总体
47.(2024八下·扶沟期中)如图,在平行四边形ABCD中,AB=4,∠BAD的平分线与BC的延长线交于点E,与DC交于点F,且点F为边DC的中点,DG⊥AE,垂足为G,若DG=1,则AE的边长为( )
A. B. C.4 D.8
48.(2024八下·卢龙期中)向最大容量为60升的热水器内注水,每分钟注水10升,注水2分钟后停止1分钟,然后继续注水,直至注满.则能反映注水量与注水时间函数关系的图象是 ( )
A. B.
C. D.
49.(2024八下·新乡期中)如图,E,F分别是平行四边形的边,上的点,与相交于点P,与相交于点Q,若,,,则阴影部分的面积为( )
A. B. C. D.
50.(2024八下·宣化期中)如图,在平行四边形中,对角线,相交于点O,过点O,交于点F,交于点E.若,,,则图中阴影部分的面积是( )
A.1.5 B.3 C.6 D.4
答案解析部分
1.B
2.B
解:点,横坐标为0,纵坐标为,则该点在轴负半轴上,
故答案为:B.
本题考查平面直角坐标系点的位置特征.先判断点横坐标和纵坐标的特征,再根据平面直角坐标系中点的特征进行判断可选出答案.
3.A
解:A y不是x的函数,故A项符合题意;
B y是x的函数,故B项不符合题意;
C y是x的函数,故C项不符合题意;
D y=5-y,y是x的函数,故D项不符合题意.
故答案为:A.
根据函数的定义可知,对于每一个确定的x的值,y都有唯一确定的值与其对应,即可判断.
4.C
解:过点P作直线l使AD⊥l,分别交AD,BC于点M,N,如图,
则MN⊥AD,
∵ 四边形ABCD为平行四边形,
∴ MN⊥BC,
∴ S=,
S1=,
S2=,
∴ .
故答案为:C.
过点P作直线l使AD⊥l,分别交AD,BC于点M,N,根据平行四边形的性质可得MN⊥BC,根据平行四边形的面积公式和三角形的面积公式,即可求得.
5.C
6.C
7.C
解:∵在频数分布直方图中各小长方形的高的比等于频数之比,
∴各个小组的频数比为,则对应的小长方形的高的比为.
故答案为C.
本题考查频数分布直方图的特点.根据频数分布直方图中各小长方形的高的比等于频数之比,据此可选出答案.
8.B
9.B
10.A
解:由题意得点向下平移5个单位长度即纵坐标-5,
∴平移后得到对应点的坐标为,
故答案为:A
根据坐标与图形的变化-平移结合题意即可求解。
11.B
12.D
13.D
解:根据正方形的判别方法知,两条对角线互相垂直平分的四边形是菱形,且相等又可判定为正方形,故选D.
两条对角线互相垂直平分的四边形是菱形,对角线相等的菱形是正方形,所以该四边形是正方形.
14.D
解:∵AE=10,BE=24,即24和10为两条直角边长时,
小正方形的边长=24-10=14,
∴EF=.
故答案为:D.
先求出小正方形的边长,再利用勾股定理求出EF的长即可。
15.C
解:要反映每天的气温升高、降低的变化情况,因此选择折线统计图较好,
故答案为:C.
本题考查统计图的选择.根据题意:要反映经开区年月份每天的最高气温的变化情况,因此符合折线统计图的特点,因此选择折线统计图比较合适.
16.C
解:
∵观察某一段时间内温度的变化,
∴适合选取折线统计图,
故答案为:C
根据每种统计图的特点进行选取即可求解。
17.B
解:A、邻边相等的矩形是正方形,A不符合题意;
B、矩形的对角线相等,但对角线相等的矩形不一定是正方形,B符合题意;
C、∵四边形是矩形,
∴,,
∵,
∴,
∴矩形为正方形,C不符合题意;
D、∵,,
∴,
∴,
∴,
∴矩形是正方形,D不符合题意
故答案为:B
根据正方形的判定与性质,矩形的判定与性质结合题意添加条件即可求解。
18.A
解:A、社会上的传闻很多是人们道听途说的,可信度比较低,故本选项符合题意,A正确;
B、从报纸上摘录的信息,因为报纸是国家正规报纸,所以可信度很高,故本选项不合题意,B错误;
C、电视上的新闻报道的大都是事实事件,所以可信度很高,故本选项不合题意,C错误;
D、考察或测量得到的可信度很高,故本选项不合题意,D错误.
故答案为:A.
本题考查调查收集数据的过程与方法.根据传闻可信度比较低可判断A选项;根据报纸可信度很高,据此可判断B选项;根据电视上的新闻报道可信度很高可判断C选项;根据考察或测量可信度很高据此可判断D选项.
19.B
20.A
21.B
22.B
23.B
24.A
25.A
解:A、当x取一值时,y没有唯一与它对应的值,y不是x的函数,故答案为项A符合题意,A错误;
B、当x取一值时,y有唯一与它对应的值,y是x的函数,故答案为项B不合题意,B错误;
C、当x取一值时,y有唯一与它对应的值,y是x的函数,故答案为项C不合题意,C错误;
D、当x取一值时,y有唯一与它对应的值,y是x的函数,故答案为项D不合题意,D错误;
故答案为A.
本题考查函数的概念.根据函数的概念:当x取一值时,y有唯一与它对应的值.进行逐项判断可选出答案.
26.C
27.A
解:把点代入正比例函数解析式中,
得,
解得,
故答案为A.
本题考查图象过点问题.把点代入正比例函数解析式中,通过化简可求出的值.
28.C
29.A
30.D
解:令x=0, ,
∴一次函数的图象与轴的交点的坐标为.
故答案为:D
本题考查一次函数的图象和性质.令x=0,可求出函数值,据此可求出图象与轴的交点的坐标.
31.C
解:由作图得:平分,
∴,
在中,,,,
∴,
∴,
∴,
∴,
故答案为:.
根据角平分线定义可得,再根据平行四边形性质可得,,,则,即,根据等角对等边可得,再根据边之间的关系即可求出答案.
32.A
解:A、了解班级每位同学穿鞋的尺码,适合全面调查,选项说法正确,符合题意,A正确;
B、了解中学生的心理健康状况,适合抽样调查,选项说法错误,不符合题意,B错误;
C、调查长江水质情况,适合抽样调查,选项说法错误,不符合题意,C错误;
D、了解市民做高铁出行的意愿,适合抽样调查,选项说法错误,不符合题意,D错误;
故答案为:A.
本题考查全面调查和抽样调查的定义.根据全面调查的定义: 是对需要调查的对象逐个调查; 抽样调查的定义: 在被调查对象的总体中,抽取若干个体作为样本进行调查,然后根据对样本的调查结果来推导总体的一般特征; ,逐项进行判断可选出答案.
33.C
解:以甲为坐标原点,乙的位置是(2,3),则以乙为坐标原点,甲的位置是(-2,-3);
以丙为坐标原点,乙的位置是(-3,-2),则以乙为坐标原点,丙的位置是(3,2).
故答案为:C.
本题考查坐标确定位置.由于已知三人建立坐标系时,x轴y轴正方向相同,根据:直角坐标平面内点的位置由有序实数对确定,有序实数对与点一一对应,则以甲为坐标原点,乙的位置是(2,3),则以乙为坐标原点,甲的位置是(-2,-3);同样得到以丙为坐标原点,乙的位置是(-3,-2),则以乙为坐标原点,丙的位置是(3,2).
34.D
解:A、当x=2时,y=-2+6=4≠1,A错误;
B、图象向上平移1个单位长度后得到的函数解析式为,B错误;
C、k=-1<0,b=6>0,
其图像经过第一、二、四象限,C错误;
D、k=-1<0,
y随x的增大而减小,
1>-1,
,D正确.
故答案为:D.
把x=2代入表达式求出y的值即可判断A;根据平移的性质为上加下减即可判断B;由k=-1<0,b=6>0,得出一次函数所经过的象限即可判断C;由k<0,得到y随x的增大而减小即可判断D.
35.D
36.A
解:∵,
∴.
∴.
∵平分,
∴.
∴.
∴.
同理可得.
∴.
故答案为:A.
根据平行四边形性质可得,则,再根据角平分线定义可得,则,再根据等角对等边可得,同理可得,再根据边之间的关系即可求出答案.
37.B
解:任意多边形的外角和等于360°,
A、三角形的内角和等于180°,180°不等于360°,不符合题意;
B、四边形的内角和等于360°,360°等于360°,符合题意;
C、五边形的内角和等于540°,540°不等于360°,不符合题意;
D、六边形的内角和等于720°,720°不等于360°,不符合题意.
故答案为:B.
根据任意多边形的外角和等于360°,要使内角和等于外角和,利用公式求出多边形内角和即可判断.
38.C
39.C
解:∵四边形ABCD是平行四边形,
∴∠B=∠D,∠A+∠B=180°,
∵∠B+∠D=100°,
∴∠B=∠D=50°,
∴∠A=130°,
故答案为:C.
由四边形ABCD是平行四边形,得出∠A+∠B=180°,即可求解∠B的度数,再利用平行四边形的邻角互补求得答案即可。
40.C
解:先设矩形中某个点的坐标为,则由一矩形上各点的纵坐标不变,横坐标变为原来的,可知该点的坐标变为,
∴该矩形发生的变化为横向压缩原来的一半;
故答案为C.
本题考查平面直角坐标系点的坐标特征及矩形的性质.先设矩形中某个点的坐标为,根据矩形的性质、平移的性质可求出该点的坐标变为,据此可找出矩形发生的变化,选出答案.
41.D
解:∵洗衣机工作前洗衣机内无水,
∴A,B两选项不正确,被淘汰;
又∵洗衣机最后排完水,
∴C选项不正确,被淘汰,
所以选项D正确.
故选:D.
根据洗衣机内水量开始为0,清洗时水量不变,排水时水量变小,直到水量0,即可得到答案.
42.C
解:根据题意,得,
故,
故答案为C.
本题考查了一次函数的应用.根据耗油量+剩油量=100,据此可列出式子,再进行变形可得到答案.
43.C
解:∵四边形ABCD是平行四边形,AC=12,
∴OA=AC=6,BD=2OB,
∵AB⊥AC,AB=8,
∴OB==10,
∴BD=2OB=20.
故选C.
由四边形ABCD是平行四边形,根据平行四边形的对角线互相平分,可得OA的长,然后由AB⊥AC,AB=8,AC=12,根据勾股定理可求得OB的长,继而求得答案.
44.B
解:5楼6号、希望路20号、东经,北纬都能确定物体的具体位置,
北偏东不能确定物体的具体位置,
故答案为:B.
本题考查坐标确定位置.根据坐标确定位置.:一对有序实数对才能确定一个点的位置.在平面直角坐标系中,要用两个数据才能表示一个点的位置.北偏东只有一个数据,故不能确定一个位置.
45.D
解:已知第一个矩形的面积为1;
第二个矩形的面积为原来的()2×2-2=;
第三个矩形的面积是()2×3-2=;
…
故第n个矩形的面积为:= .
故答案为:D.
先求出第二个矩形的面积为,第三个矩形的面积是,依次类推,可得第n个矩形的面积为,即可判断.
46.A
47.B
48.D
解:注水需要60÷10=6分钟,注水2分钟后停止注水1分钟,共经历6+1=7分钟,排除A、B;再根据停1分钟,再注水4分钟,排除C.
故答案为:D.
先计算出注水所需的时间,即60÷10=6分钟,由于中途休息了1分钟,则共需要7分钟,由题意得2到3分钟之间休息,则2到3分钟之间线段与x轴平行.
49.B
50.C
同课章节目录
