期中真题专项复习02 填空题(含答案)--2024-2025学年七年级数学下册(华师大版2024)
文档属性
| 名称 | 期中真题专项复习02 填空题(含答案)--2024-2025学年七年级数学下册(华师大版2024) |  | |
| 格式 | docx | ||
| 文件大小 | 324.0KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-03-30 11:35:12 | ||
图片预览




文档简介
2024-2025学年七年级数学下册(华师大版2024)
期中真题专项复习02 填空题
一、填空题
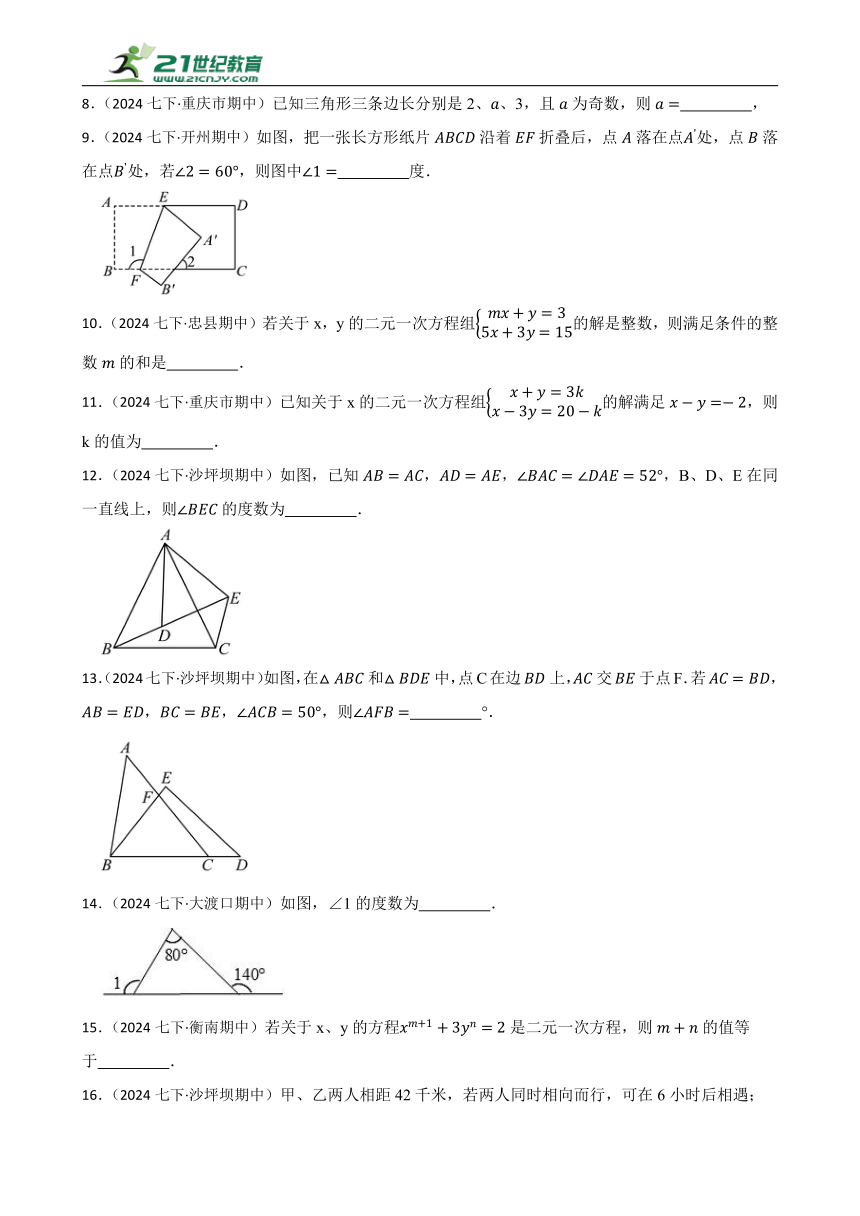
1.(2024七下·海口期中)如图,在△MBC中,∠ABC、∠ACB的角平分线OB、OC交于点O,若∠O=m°,则∠A的度数是 °(用含m的代数式表示).
2.(2024七下·彭山期中)已知某商品的进价为65元,按标价打八折售出后仍盈利15元,则该商品的标价为 .
3.(2024七下·江津期中)如图,将一张长方形纸片如图所示折叠后,再展开.如果∠1=66°,那么∠2= .
4.(2023七下·江北期中)若方程组是二元一次方程组,则“……”可以是 .
5.(2024七下·江津期中)若是整数,关于、的二元一次方程组的解是整数,则满足条件的所有的值的和为 .
6.(2024七下·重庆市期中)如图,在锐角中,分别是边上的点,,,且交于点F.若,则的大小是 .
AI
7.(2024七下·遂宁期中)如果方程是关于的一元一次方程,那么 .
8.(2024七下·重庆市期中)已知三角形三条边长分别是2、、3,且为奇数,则 ,
9.(2024七下·开州期中)如图,把一张长方形纸片沿着折叠后,点落在点处,点落在点处,若,则图中 度.
10.(2024七下·忠县期中)若关于x,y的二元一次方程组的解是整数,则满足条件的整数的和是 .
11.(2024七下·重庆市期中)已知关于x的二元一次方程组的解满足,则k的值为 .
12.(2024七下·沙坪坝期中)如图,已知,,,B、D、E在同一直线上,则的度数为 .
13.(2024七下·沙坪坝期中)如图,在和中,点C在边上,交于点F.若,,,,则 °.
14.(2024七下·大渡口期中)如图,∠1的度数为 .
15.(2024七下·衡南期中)若关于x、y的方程是二元一次方程,则的值等于 .
16.(2024七下·沙坪坝期中)甲、乙两人相距42千米,若两人同时相向而行,可在6小时后相遇;而若两人同时同向而行,乙可在14小时后追上甲,设甲的速度为x千米/时,乙的速度为y千米/时,列出的二元一次方程组为 .
17.(2024七下·重庆市期中)如图,在中,已知D、E、F分别为的中点,且的面积等于,则阴影部分面积为 .
18.(2024七下·重庆市期中)等腰三角形两腰上的高所在的直线形成的锐角为,则该等腰三角形的底角的度数为 .
19.(2024七下·铜梁期中)某同学家到学校之间只有一段上坡和一段平路.如果该同学保持上坡速度米分,平路速度米分,下坡速度米分,那么他从家到学校需要分钟,从学校回家需要分钟.则该同学家到学校全程是 米.
20.(2024七下·铜梁期中)关于的二元一次方程组中,,则 ;
21.(2024七下·忠县期中)如图,点C、D在线段上,点C是线段的中点,.若,则 .
22.(2024七下·北碚期中)五一假期即将到来,销售重庆特产的某商户准备继续推出去年较火的三种特产礼盒进行售卖.去年五一节期间,三种礼盒的销量比为,其中礼盒的售价为礼盒的售价的倍,且礼盒的销售额为礼盒的销售额的倍.今年由于成本变化,礼盒售价上调,礼盒售价有一定提高,礼盒售价与去年保持不变,该商家预估今年礼盒和礼盒的销量也与去年保持不变,如果今年总的销售额上涨且礼盒与礼盒的销售额之比为,则今年礼盒与礼盒的售价之比为 .
23.(2024七下·北碚期中)如图,四边形中,,点、点在上,将沿折叠,点落在点处,线段所在的直线平分,将沿折叠,点刚好落在线段上的点处,且两条折痕形成的,则 .
24.(2024七下·潼南期中)如图,已知a∥b,∠1=70°,∠2=40°,则∠3= 度.
25.(2023七下·雁峰期中)已知方程2x﹣4=0,则x= .
26.(2024七下·蓝山期中)若方程,则用含的代数式表示得 .
27.(2024七下·重庆市期中)在△ABC中,点D为AB上的一点,且BD:AD=1:2,点E为AC上的中点,连接BE、CD交于点F,若△ABC的面积为18,则四边形AEFD的面积为 .
28.(2024七下·珠晖期中)方程组的解为 .
29.(2024七下·沙坪坝期中)如图,在中,,点在外,连接交于点,若,,则的度数为 °.
30.(2024七下·郴州期中)把方程写成用含有的代数式表示的形式 .
31.(2024七下·沙坪坝期中)如图,为钝角三角形,分别过点作边上的高,已知,,,则的长为 .
32.(2024七下·道县期中)已知,则 .
33.(2024七下·衡阳期中)若关于的方程的解是,则代数式的值为 .
34.(2024七下·黔江期中)关于x、y的二元一次方程组的解满足,则m的值是 .
35.(2024七下·武侯期中)若a,b,c分别为三角形的三边,化简:= .
36.(2024七下·江津期中)如图,将△ABC沿BC方向平移2个单位得到△DEF,若△ABC的周长等于18,则四边形ABFD的周长等于 .
37.(2024七下·江津期中)将一条两边沿互相平行的纸带按如图折叠,若,则 .
38.(2024七下·沙坪坝期中)如图,,过点A作于点F,若,则的度数是 .
39.(2024七下·沙坪坝期中)在如图所示的6×5网格中,是格点三角形(即顶点恰好是网格线的交点),则与有一条公共边且全等(不含)的所有格点三角形的个数是 .
40.(2024七下·沙坪坝期中)如图,已知点A,B,D,E在同一直线上,,,,若,则的度数为 .
41.(2024七下·秀英期中)当 时,式子与式子的值相等.
42.(2024七下·新会期中)如果方程组的解与方程组的解相同,则a+b= .
43.(2024七下·临高期中)如图,将一个矩形纸片按如图折叠,若,则的度数是 .
44.(2024七下·海口期中)若是三元一次方程组的解,则的值是 .
45.(2024七下·永州期中)已知关于、的二元一次方程组的解为,那么关于、的二元一次方程组的解为 .
46.(2024七下·衡南期中)若关于的方程的解为负数,则的取值范围是 .
47.(2023七下·雁峰期中)如图,在△ABC中,∠BAC=90°,AD是高,BE是中线,CF是角平分线,CF交AD于点G,下面说法中正确的有 (请填写序号).
①S△ABE=S△BCE;②∠AFG=∠AGF;③∠FAG=2∠ACF.
48.(2023七下·雁峰期中)如图,∠A=40°,∠CBD是△ABC的外角,∠CBD=120°,则∠C是 度.
49.(2023七下·北仑期中)一副直角三角尺叠放如图1所示,现将45°的三角尺ADE固定不动,将含30°的三角尺ABC绕顶点A顺时针转动(旋转角不超过180度),使两块三角尺至少有一组边互相平行.如图2:当∠BAD=15°时,BC∥DE.则∠BAD(0°<∠BAD<180°)其它所有可能符合条件的度数为 .
50.(2024七下·沙坪坝期中)已知二元一次方程,用含y的代数式表示x,则 .
答案解析部分
1.(2m-180)
2.100元
3.48°
4.(答案不唯一)
解:∵是二元一次方程组 ,
∴"······"可以是x-y=0;
故答案为:x-y=0(答案不唯一).
根据二元一次方程组的定义进行求解即可.
5.-12
6.
7.3
8.3
9.
10.3
11.
12.
13.100
14.
15.1
16.
17.
18.或
19.
20.
21.18
解:设,
,
,
,
点C为线段的中点,
,
,
,
.
故答案为:18.
设,根据题意可得出,根据点C是线段的中点,得出的长度,结合建立等式,即可求出x的值,即可求解.
22.
23.
24.70
解:由对顶角相等可得∠ACB=∠2=40°,
在△ABC中,由三角形内角和知∠ABC=180°-∠1-∠ACB=70°.
又∵a∥b,
∴∠3=∠ABC=70°.
故答案为:70.
由对顶角相等可得∠ACB=∠2=40°,根据三角形的内角和定理算出∠ABC的度数,最后根据二直线平行,内错角相等得出∠3=∠ABC=70°.
25.2
解:2x-4=0,
移项得:2x=4,
系数化为1得:x=2
故答案为:2.
根据解一元一次方程方法和步骤操作计算即可.
26.
解:,
移项得:3x=1-4y,
两边同时除以3得: ,
用含的代数式表示得: .
故答案为: .
根据等式的性质将x的系数化为1即可得到答案.
27.7.5
28.
29.
30.
31.6
32.1
33.
34.2
35.
36.22
37.65°
38.
39.7个
40.
41.
42.1
解:依题意,知是方程组的解,
①+②,得7a+7b=7,
方程两边都除以7,得a+b=1.
两个方程组的解相同,意思是这两个方程组中的x都等于4,y都等于3,即是方程组的解,根据方程组的解的定义,即可求出a+b的值.
43.
44.
45.
46.
47.①②③
解:∵BE是中线,
∴AE=CE,
∴S△ABE=S△BCE, 故①正确,符合题意;
∵CF平分∠ACB,
设∠ACF=∠BCF=x,
∵AD是高线,
∴∠ADC=∠BAC=90°,
∴∠AFG=180°-∠ACF-∠CAF=90°-x,
∠AGF=∠CGD=180°-∠CDG-∠DCG=90°-x,
∴ ∠AFG=∠AGF,故②正确,符合题意;
∴∠FAG=180°-∠AFG-∠AGF=2x,
∴ ∠FAG=2∠ACF ,故③正确,符合题意;
故答案为:①②③.
由中线等积可推出①,结合题干条件,设角推理更为直观表示各个角度的关系,即推出②③;
48.80
解:在△ABC中,
∵∠BCD=∠A+∠C,
∴∠C=∠BCD-∠A=120°-40°=80°
故答案为:80.
由内角和推论,即外角的性质作差直接求得一个内角度数.
49.45°,60°,105°,135°
解:如图,
当AC∥DE时,∠BAD=∠DAE=45°;
当BC∥AD时,∠DAB=∠B=60°;
当BC∥AE时,∵∠EAB=∠B=60°,
∴∠BAD=∠DAE+∠EAB=45°+60°=105°;
当AB∥DE时,∵∠E=∠EAB=90°,
∴∠BAD=∠DAE+∠EAB=45°+90°=135°.
故答案为:45°,60°,105°,135°.
分①当AC∥DE时,②当BC∥AD时,③当BC∥AE时,④当AB∥DE时四种情况分别画出图形,然后根据平行线的性质及直角三角板的特点即可解决问题.
50.
解:
移项,得
故答案为:.
将已知的等式经过移项可把x用含y的代数式表示出来.
期中真题专项复习02 填空题
一、填空题
1.(2024七下·海口期中)如图,在△MBC中,∠ABC、∠ACB的角平分线OB、OC交于点O,若∠O=m°,则∠A的度数是 °(用含m的代数式表示).
2.(2024七下·彭山期中)已知某商品的进价为65元,按标价打八折售出后仍盈利15元,则该商品的标价为 .
3.(2024七下·江津期中)如图,将一张长方形纸片如图所示折叠后,再展开.如果∠1=66°,那么∠2= .
4.(2023七下·江北期中)若方程组是二元一次方程组,则“……”可以是 .
5.(2024七下·江津期中)若是整数,关于、的二元一次方程组的解是整数,则满足条件的所有的值的和为 .
6.(2024七下·重庆市期中)如图,在锐角中,分别是边上的点,,,且交于点F.若,则的大小是 .
AI
7.(2024七下·遂宁期中)如果方程是关于的一元一次方程,那么 .
8.(2024七下·重庆市期中)已知三角形三条边长分别是2、、3,且为奇数,则 ,
9.(2024七下·开州期中)如图,把一张长方形纸片沿着折叠后,点落在点处,点落在点处,若,则图中 度.
10.(2024七下·忠县期中)若关于x,y的二元一次方程组的解是整数,则满足条件的整数的和是 .
11.(2024七下·重庆市期中)已知关于x的二元一次方程组的解满足,则k的值为 .
12.(2024七下·沙坪坝期中)如图,已知,,,B、D、E在同一直线上,则的度数为 .
13.(2024七下·沙坪坝期中)如图,在和中,点C在边上,交于点F.若,,,,则 °.
14.(2024七下·大渡口期中)如图,∠1的度数为 .
15.(2024七下·衡南期中)若关于x、y的方程是二元一次方程,则的值等于 .
16.(2024七下·沙坪坝期中)甲、乙两人相距42千米,若两人同时相向而行,可在6小时后相遇;而若两人同时同向而行,乙可在14小时后追上甲,设甲的速度为x千米/时,乙的速度为y千米/时,列出的二元一次方程组为 .
17.(2024七下·重庆市期中)如图,在中,已知D、E、F分别为的中点,且的面积等于,则阴影部分面积为 .
18.(2024七下·重庆市期中)等腰三角形两腰上的高所在的直线形成的锐角为,则该等腰三角形的底角的度数为 .
19.(2024七下·铜梁期中)某同学家到学校之间只有一段上坡和一段平路.如果该同学保持上坡速度米分,平路速度米分,下坡速度米分,那么他从家到学校需要分钟,从学校回家需要分钟.则该同学家到学校全程是 米.
20.(2024七下·铜梁期中)关于的二元一次方程组中,,则 ;
21.(2024七下·忠县期中)如图,点C、D在线段上,点C是线段的中点,.若,则 .
22.(2024七下·北碚期中)五一假期即将到来,销售重庆特产的某商户准备继续推出去年较火的三种特产礼盒进行售卖.去年五一节期间,三种礼盒的销量比为,其中礼盒的售价为礼盒的售价的倍,且礼盒的销售额为礼盒的销售额的倍.今年由于成本变化,礼盒售价上调,礼盒售价有一定提高,礼盒售价与去年保持不变,该商家预估今年礼盒和礼盒的销量也与去年保持不变,如果今年总的销售额上涨且礼盒与礼盒的销售额之比为,则今年礼盒与礼盒的售价之比为 .
23.(2024七下·北碚期中)如图,四边形中,,点、点在上,将沿折叠,点落在点处,线段所在的直线平分,将沿折叠,点刚好落在线段上的点处,且两条折痕形成的,则 .
24.(2024七下·潼南期中)如图,已知a∥b,∠1=70°,∠2=40°,则∠3= 度.
25.(2023七下·雁峰期中)已知方程2x﹣4=0,则x= .
26.(2024七下·蓝山期中)若方程,则用含的代数式表示得 .
27.(2024七下·重庆市期中)在△ABC中,点D为AB上的一点,且BD:AD=1:2,点E为AC上的中点,连接BE、CD交于点F,若△ABC的面积为18,则四边形AEFD的面积为 .
28.(2024七下·珠晖期中)方程组的解为 .
29.(2024七下·沙坪坝期中)如图,在中,,点在外,连接交于点,若,,则的度数为 °.
30.(2024七下·郴州期中)把方程写成用含有的代数式表示的形式 .
31.(2024七下·沙坪坝期中)如图,为钝角三角形,分别过点作边上的高,已知,,,则的长为 .
32.(2024七下·道县期中)已知,则 .
33.(2024七下·衡阳期中)若关于的方程的解是,则代数式的值为 .
34.(2024七下·黔江期中)关于x、y的二元一次方程组的解满足,则m的值是 .
35.(2024七下·武侯期中)若a,b,c分别为三角形的三边,化简:= .
36.(2024七下·江津期中)如图,将△ABC沿BC方向平移2个单位得到△DEF,若△ABC的周长等于18,则四边形ABFD的周长等于 .
37.(2024七下·江津期中)将一条两边沿互相平行的纸带按如图折叠,若,则 .
38.(2024七下·沙坪坝期中)如图,,过点A作于点F,若,则的度数是 .
39.(2024七下·沙坪坝期中)在如图所示的6×5网格中,是格点三角形(即顶点恰好是网格线的交点),则与有一条公共边且全等(不含)的所有格点三角形的个数是 .
40.(2024七下·沙坪坝期中)如图,已知点A,B,D,E在同一直线上,,,,若,则的度数为 .
41.(2024七下·秀英期中)当 时,式子与式子的值相等.
42.(2024七下·新会期中)如果方程组的解与方程组的解相同,则a+b= .
43.(2024七下·临高期中)如图,将一个矩形纸片按如图折叠,若,则的度数是 .
44.(2024七下·海口期中)若是三元一次方程组的解,则的值是 .
45.(2024七下·永州期中)已知关于、的二元一次方程组的解为,那么关于、的二元一次方程组的解为 .
46.(2024七下·衡南期中)若关于的方程的解为负数,则的取值范围是 .
47.(2023七下·雁峰期中)如图,在△ABC中,∠BAC=90°,AD是高,BE是中线,CF是角平分线,CF交AD于点G,下面说法中正确的有 (请填写序号).
①S△ABE=S△BCE;②∠AFG=∠AGF;③∠FAG=2∠ACF.
48.(2023七下·雁峰期中)如图,∠A=40°,∠CBD是△ABC的外角,∠CBD=120°,则∠C是 度.
49.(2023七下·北仑期中)一副直角三角尺叠放如图1所示,现将45°的三角尺ADE固定不动,将含30°的三角尺ABC绕顶点A顺时针转动(旋转角不超过180度),使两块三角尺至少有一组边互相平行.如图2:当∠BAD=15°时,BC∥DE.则∠BAD(0°<∠BAD<180°)其它所有可能符合条件的度数为 .
50.(2024七下·沙坪坝期中)已知二元一次方程,用含y的代数式表示x,则 .
答案解析部分
1.(2m-180)
2.100元
3.48°
4.(答案不唯一)
解:∵是二元一次方程组 ,
∴"······"可以是x-y=0;
故答案为:x-y=0(答案不唯一).
根据二元一次方程组的定义进行求解即可.
5.-12
6.
7.3
8.3
9.
10.3
11.
12.
13.100
14.
15.1
16.
17.
18.或
19.
20.
21.18
解:设,
,
,
,
点C为线段的中点,
,
,
,
.
故答案为:18.
设,根据题意可得出,根据点C是线段的中点,得出的长度,结合建立等式,即可求出x的值,即可求解.
22.
23.
24.70
解:由对顶角相等可得∠ACB=∠2=40°,
在△ABC中,由三角形内角和知∠ABC=180°-∠1-∠ACB=70°.
又∵a∥b,
∴∠3=∠ABC=70°.
故答案为:70.
由对顶角相等可得∠ACB=∠2=40°,根据三角形的内角和定理算出∠ABC的度数,最后根据二直线平行,内错角相等得出∠3=∠ABC=70°.
25.2
解:2x-4=0,
移项得:2x=4,
系数化为1得:x=2
故答案为:2.
根据解一元一次方程方法和步骤操作计算即可.
26.
解:,
移项得:3x=1-4y,
两边同时除以3得: ,
用含的代数式表示得: .
故答案为: .
根据等式的性质将x的系数化为1即可得到答案.
27.7.5
28.
29.
30.
31.6
32.1
33.
34.2
35.
36.22
37.65°
38.
39.7个
40.
41.
42.1
解:依题意,知是方程组的解,
①+②,得7a+7b=7,
方程两边都除以7,得a+b=1.
两个方程组的解相同,意思是这两个方程组中的x都等于4,y都等于3,即是方程组的解,根据方程组的解的定义,即可求出a+b的值.
43.
44.
45.
46.
47.①②③
解:∵BE是中线,
∴AE=CE,
∴S△ABE=S△BCE, 故①正确,符合题意;
∵CF平分∠ACB,
设∠ACF=∠BCF=x,
∵AD是高线,
∴∠ADC=∠BAC=90°,
∴∠AFG=180°-∠ACF-∠CAF=90°-x,
∠AGF=∠CGD=180°-∠CDG-∠DCG=90°-x,
∴ ∠AFG=∠AGF,故②正确,符合题意;
∴∠FAG=180°-∠AFG-∠AGF=2x,
∴ ∠FAG=2∠ACF ,故③正确,符合题意;
故答案为:①②③.
由中线等积可推出①,结合题干条件,设角推理更为直观表示各个角度的关系,即推出②③;
48.80
解:在△ABC中,
∵∠BCD=∠A+∠C,
∴∠C=∠BCD-∠A=120°-40°=80°
故答案为:80.
由内角和推论,即外角的性质作差直接求得一个内角度数.
49.45°,60°,105°,135°
解:如图,
当AC∥DE时,∠BAD=∠DAE=45°;
当BC∥AD时,∠DAB=∠B=60°;
当BC∥AE时,∵∠EAB=∠B=60°,
∴∠BAD=∠DAE+∠EAB=45°+60°=105°;
当AB∥DE时,∵∠E=∠EAB=90°,
∴∠BAD=∠DAE+∠EAB=45°+90°=135°.
故答案为:45°,60°,105°,135°.
分①当AC∥DE时,②当BC∥AD时,③当BC∥AE时,④当AB∥DE时四种情况分别画出图形,然后根据平行线的性质及直角三角板的特点即可解决问题.
50.
解:
移项,得
故答案为:.
将已知的等式经过移项可把x用含y的代数式表示出来.
同课章节目录
