期中真题专项复习02 填空题(含答案)--2024-2025学年七年级数学下册(冀教版2024)
文档属性
| 名称 | 期中真题专项复习02 填空题(含答案)--2024-2025学年七年级数学下册(冀教版2024) |  | |
| 格式 | docx | ||
| 文件大小 | 583.1KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-03-30 11:36:09 | ||
图片预览



文档简介
2024-2025学年七年级数学下册(冀教版2024)
期中真题专项复习02 填空题
一、填空题
1.(2024七下·保定期中)如图1,在中,,的角平分线交于点O,则.
如图2,在中,,的两条三等分角线分别对应交于,,则,则 .
根据以上阅读理解,如图3、猜想(n等分时,内部有个点)(用n的代数式表示) .
2.(2024七下·唐山期中)平面直角坐标系中,点A的坐标为,将点A沿水平方向向右平移2个单位长度得到点B,则点B的坐标为 ,又将点B向下平移5个单位长度点C,则点C的坐标为 .
3.(2024七下·石家庄期中)如图,已知,,则 度.
4.(2024七下·保定期中)已知则 .
5.(2024七下·石家庄期中)如图,AD是△ABC的中线,点E为AD的中点,点F为BE的中点,S△ABC=41,则S△BFC= .
6.(2024七下·石家庄期中)(1)计算: .
(2)计算: .
7.(2024七下·石家庄期中)已知是关于x,y的二元一次方程,则 .
8.(2024七下·石家庄期中)已知,则 .
9.(2024七下·石家庄期中)计算
(1) .
(2) .
10.(2024七下·保定期中)如图,△ABC≌△A'B'C',其中∠A=36°,∠C'=24°,则∠B= 度.
11.(2024七下·东光期中)已知二元一次方程x﹣2y﹣1=0,若用含x的代数式表示y,可得 y= .
12.(2024七下·定州期中)在平面直角坐标系中,线段CD是由线段AB平移得到的,点的对应点,则点的对应点D的坐标为 .
13.(2024七下·柯桥期中)如果(x+3)(x+a)=x2﹣2x﹣15,则a= .
14.(2024七下·石家庄期中)如图,已知,则 ,则等于 (用含的式子表示).
15.(2024七下·石家庄期中)已知:如图,直线,,若,则 .
16.(2024七下·石家庄期中)把命题“两直线平行,同旁内角互补”改写成如果 ,那么 .
17.(2024七下·慈溪期中)如图,将直角三角形ABC沿AB方向平移4个单位长度得到三角形DEF,CG=3,EF=7,则图中阴影部分的面积为 .
18.(2024七下·丛台期中)如图,直线,点在上,点在上,点在之间,和的角平分线相交于点的角平分线交的反向延长线于点,下列四个结论:
①;
②;
③若,则;
④.
其中正确的结论是 (填写序号).
19.(2024七下·桥西期中)如图,已知,,则的度数为 .
20.(2024七下·桥西期中) .
21.(2024七下·竞秀期中)在,,三个内角中最大内角的度数为 ,的形状为 .
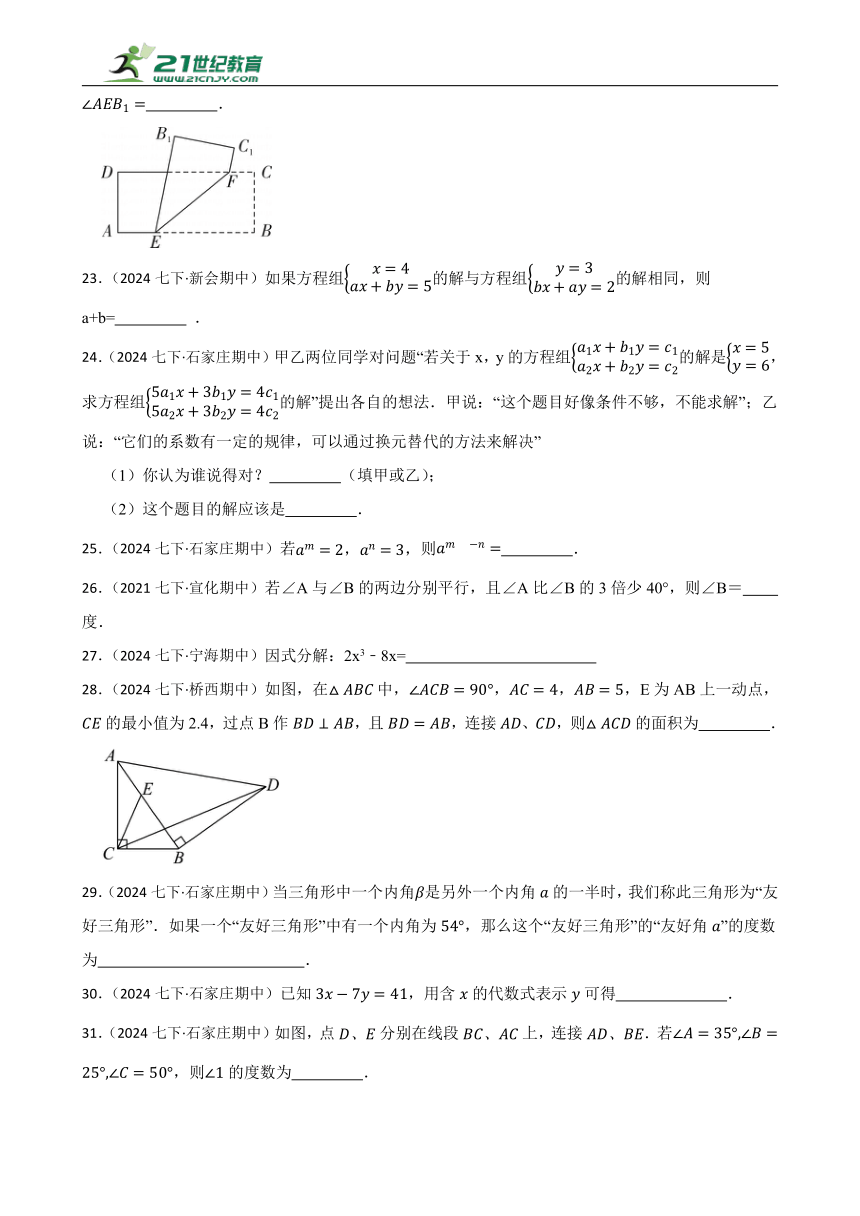
22.(2024七下·威县期中)如图,将长方形纸片ABCD沿直线EF折叠.若∠DFE=40°,则 .
23.(2024七下·新会期中)如果方程组的解与方程组的解相同,则a+b= .
24.(2024七下·石家庄期中)甲乙两位同学对问题“若关于x,y的方程组的解是,求方程组的解”提出各自的想法.甲说:“这个题目好像条件不够,不能求解”;乙说:“它们的系数有一定的规律,可以通过换元替代的方法来解决”
(1)你认为谁说得对? (填甲或乙);
(2)这个题目的解应该是 .
25.(2024七下·石家庄期中)若则 .
26.(2021七下·宣化期中)若∠A与∠B的两边分别平行,且∠A比∠B的3倍少40°,则∠B= 度.
27.(2024七下·宁海期中)因式分解:2x3﹣8x=
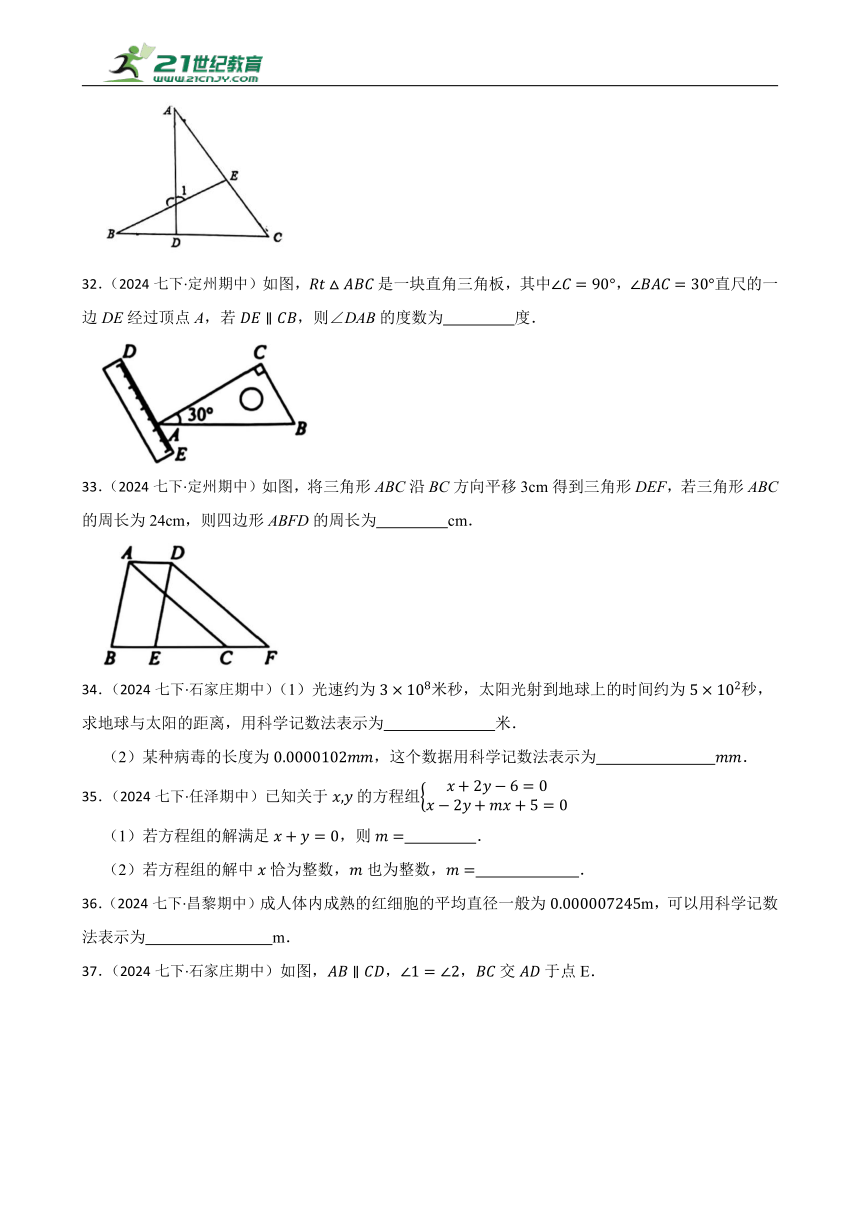
28.(2024七下·桥西期中)如图,在中,,,,E为AB上一动点,的最小值为2.4,过点B作,且,连接、,则的面积为 .
29.(2024七下·石家庄期中)当三角形中一个内角是另外一个内角的一半时,我们称此三角形为“友好三角形”.如果一个“友好三角形”中有一个内角为,那么这个“友好三角形”的“友好角”的度数为 .
30.(2024七下·石家庄期中)已知,用含的代数式表示可得 .
31.(2024七下·石家庄期中)如图,点分别在线段上,连接.若,则的度数为 .
32.(2024七下·定州期中)如图,是一块直角三角板,其中,直尺的一边DE经过顶点A,若,则∠DAB的度数为 度.
33.(2024七下·定州期中)如图,将三角形ABC沿BC方向平移3cm得到三角形DEF,若三角形ABC的周长为24cm,则四边形ABFD的周长为 cm.
34.(2024七下·石家庄期中)(1)光速约为米秒,太阳光射到地球上的时间约为秒,求地球与太阳的距离,用科学记数法表示为 米.
(2)某种病毒的长度为,这个数据用科学记数法表示为 .
35.(2024七下·任泽期中)已知关于的方程组
(1)若方程组的解满足,则 .
(2)若方程组的解中恰为整数,也为整数, .
36.(2024七下·昌黎期中)成人体内成熟的红细胞的平均直径一般为m,可以用科学记数法表示为 m.
37.(2024七下·石家庄期中)如图,,,交于点E.
(1)如图1,若于点D,,则的度数为 °;
(2)如图2,与的平分线交于点P,若,求的 °.
38.(2024七下·丰润期中)已知关于x,y的二元一次方程组的解满足,则k的值为 .
39.(2024七下·保定期中)如图,D、E分别是△ABC边AB、BC上的点,AD=2BD,BE=CE,设△ADF的面积为,△FCE的面积为,若S△ABC=24,则-的值为 .
40.(2024七下·襄都期中)如图,这是某校劳动实践基地的两块边长分别为的正方形用地,,其中种菜,种花,不能使用的部分(阴影部分)为,面积为.
(1)种菜和花的总面积为 (用含的代数式表示).
(2)经测量,与之和为8米,种菜的面积比种花的面积多了16平方米,则比长 米.
41.(2024七下·保定期中)如图,一块含30°角的直角三角尺,两个顶点分别在直尺的一对平行边上,若∠=110°,则∠= °.
42.(2024七下·桥西期中)如图,已知,,则的度数为 .
43.(2024七下·东光期中)如图,甲所示三角形纸片中,,将纸片沿过点B的直线折叠,使点C落到边上的E点处,折痕为(如图乙).再将纸片沿过点E的直线折叠,点A恰好与点D重合,折痕为(如图丙),则的大小为 .
44.(2024七下·保定期中)如图,从边长为的正方形纸片中剪去一个边长为的正方形,剩余部分沿虚线又剪拼成一个矩形(不重叠无缝隙),则矩形的面积为 .
45.(2023七下·孝南期中)把命题“相等的角是对顶角”改写成“如果…,那么…”的形式是
46.(2024七下·保定期中)如图,在中,点,点分别是,的中点,若的面积为1,则的面积为 .
47.(2024七下·献县期中)如图,直线,相交于点,过点作,射线平分,,则的度数为 ,的度数为 .
48.(2024七下·竞秀期中)如图,已知,点是上一点,交于点.
(1)与CF的位置关系是;
(2)若,,则的长为.
49.(2024七下·竞秀期中)若,则.
50.(2024七下·竞秀期中)如图,在中,为的中点,连接,取的中点,连接若的面积是1,则的面积是.
答案解析部分
1.;
2.;
3.
4.2
解:,
∴2m+3=7,
解得:m=2,
故答案为:2.
利用同底数幂的乘方及幂的乘方的计算方法可得,即可得到2m+3=7,最后求出m的值即可.
5..
6.;
7.
8.40
9.;
10.120
11.
12.
∵线段CD是由线段AB平移得到的,点的对应点,
∴线段CD是由线段AB先向右平移4个单位长度,再向上平移3个单位长度得到,
∵点B的坐标为(-4,-1),
∴点D的坐标为(-4+4,-1+3),即(0,2),
故答案为(0,2).
先利用点A、C的坐标证出线段CD是由线段AB先向右平移4个单位长度,再向上平移3个单位长度得到,再结合点B的坐标求出点D的坐标即可.
13.﹣5
解:(x+3)(x+a)=x2+(a+3)x+3a=x2﹣2x﹣15,
可得:a+3=﹣2,
解得:a=﹣5.
故答案为:﹣5.
已知等式左边利用多项式乘多项式法则计算,合并后利用多项式相等的条件即可求出a的值.
14.;
15.
16.两直线平行;同旁内角互补
17.22
解:∵Rt△ABC沿AB的方向平移AD距离得△DEF,
∴△DEF≌△ABC,
∴EF=BC=7,S△DEF=S△ABC,
∴S△ABC﹣S△DBG=S△DEF﹣S△DBG,
∴S四边形ACGD=S梯形BEFG,
∵CG=3,
∴BG=BC﹣CG=7﹣3=4,
∴S梯形BEFG (BG+EF) BE (4+7)×4=22.
故答案为:22.
根据平移的性质可得△DEF≌△ABC,即得S△DEF=S△ABC,从而求出S四边形ACGD=S梯形BEFG,根据梯形的面积公式计算即可.
18.①②④
19.70
解:如图所示:
∵a//b,∠1=110°,
∴∠3=∠1=110°,
∴∠2=180°-∠3=70°,
故答案为:70°.
利用平行线的性质可得∠3=∠1=110°,再利用邻补角求出∠2=180°-∠3=70°即可.
20.1
解:,
故答案为:1.
利用0指数幂的性质及计算方法分析求解即可.
21.;钝角三角形
22.100°
解:∵四边形ABCD是长方形,
∴DC∥AB.
∴∠DFE=∠FEB=40°.
∵折叠,
∴∠B1EF=∠FEB=40°.
∴∠AEB1=180°-∠FEB-∠B1EF=180°-40°-40°=100°.
故答案为:100°.
解题关键是结合平行线的性质与折叠的性质,解出∠FEB的度数和∠B1EF=∠FEB.
23.1
解:依题意,知是方程组的解,
①+②,得7a+7b=7,
方程两边都除以7,得a+b=1.
两个方程组的解相同,意思是这两个方程组中的x都等于4,y都等于3,即是方程组的解,根据方程组的解的定义,即可求出a+b的值.
24.乙;
25.
26.55或20
解:∵∠A与∠B的两边分别平行,
∴∠A+∠B=180°①,∠A=∠B②,
∵∠A比∠B的3倍少40°,
∴∠A=3∠B﹣40°③,
把③代入①得:3∠B﹣40°+∠B=180°,
∠B=55°,
把③代入②得:3∠B﹣40°=∠B,
∠B=20°,
故答案为:55或20.
根据题意当∠A与∠B的两边分别平行时,分为两种情况:∠A+∠B=180°,∠A=∠B,分别与∠A=3∠B﹣40°组成方程组,求解即可。
27. 2x(x+2)(x﹣2)
解:2x3﹣8x=2x(x2﹣4)=2x(x+2)(x﹣2).
故答案为:2x(x+2)(x﹣2).
先提公因式2x,分解成2x(x2﹣4),而x2﹣4可利用平方差公式分解.
28.14
29.或或
解:根据题意可得:,
①当时,,
解得:,
②当时,“友好角a”的度数为,
③当,时,
,
即,
解得:
综上:“友好角a”的度数为或或,
故答案为:或或.
分三种情况:①当时 ,②当时,③当,时,分别根据三角形内角和定理建立方程求解.
30.
解:∵,
∴,
∴,
故答案为:.
移项,化系数为1,据此求解.
31.
解:∵∠1=∠2=180° (∠B+∠ADB),∠ADB=∠A+∠C,
又∵,,,
∴∠1=180° (∠B+∠A+∠C)
=180° (25°+35°+50°)
=180° 110°
=70°
故答案为:70°.
由三角形的内角和定理,可得∠1=∠2=180 (∠B+∠ADB),根据外角的性质可得∠ADB=∠A+∠C,所以∠1=180° (∠B+∠A+∠C),由此解答即可.
32.120
∵,,
∴∠DAC=∠C=90°,
∵,
∴∠DAB=∠DAC+∠BAC=90°+30°=120°,
故答案为:120.
利用平行线的性质可得∠DAC=∠C=90°,再利用角的运算求出∠DAB=∠DAC+∠BAC=90°+30°=120°即可.
33.30
∵将三角形ABC沿BC方向平移3cm得到三角形DEF,且三角形ABC的周长为24cm,
∴AD=CF=3cm,AB+BC+AC=AB+BC+DF=24cm,
∴C四边形ABFD=AB+BC+DF+AD+CF=24+3+3=30cm,
故答案为:30.
利用平移的性质可得AD=CF=3cm,AB+BC+AC=AB+BC+DF=24cm,再利用四边形的周长公式及等量代换求解即可.
34.;
35.;或
36.
37.25;55
38.4
39.4
解:∵AD=2BD,
∴S△CBD= 13S△ABC=13×24=8 , ∵BE=CE,
∴S△ABE=,
∴S△ABE-S△CBD=(S1+S四边形BDFE)-(S2+S四边形BDFE)=S1-S2=12-8=4。
故答案为:4.
首先根据等高三角形面积之间的关系,求得S△CBD= 13S△ABC=13×24=8 ,S△ABE=,进而得出S△ABE-S△CBD=(S1+S四边形BDFE)-(S2+S四边形BDFE)=S1-S2=12-8=4。
40.;2
41.50
解:∵直尺的对边平行,
∴∠1=180°-α=180°-110°=70°,
∵∠2=60°,
∴∠β=180°-70°-60°=50°。
故答案为:50.
首先根据平行线的性质得出∠1=180°-α=180°-110°=70°,再根据平角的定义即可得出∠β=180°-70°-60°=50°。
42.70
43.120
44.
45.如果两个角是对顶角,那么两个角相等
解:∵原命题的条件是:“两个角是对顶角”,结论是:“这两个角相等”,
∴命题“对顶角相等”写成“如果…那么…”的形式为:“如果两个角是对顶角,那么两个角相等”,
故答案为:如果两个角是对顶角,那么两个角相等.
对顶角相等的条件是两个角是对顶角,结论是两角相等,据此即可改写成“如果…,那么…”的形式.
46.4
解:∵点E是AB的中点,的面积为1,
∴S△ADE=S△BDE=1,
∴S△ABD=S△ADE+S△BDE=1+1=2,
∵点D是BC的中点,
∴S△ADC=S△ABD=2,
∴S△ABC=S△ADC+S△ABD=2+2=4,
故答案为:4.
利用三角形中线平分三角形的面积可得S△ADE=S△BDE=1,S△ADC=S△ABD=2,再求出S△ABC=S△ADC+S△ABD=2+2=4即可.
47.;
48.,
49.27
50.
期中真题专项复习02 填空题
一、填空题
1.(2024七下·保定期中)如图1,在中,,的角平分线交于点O,则.
如图2,在中,,的两条三等分角线分别对应交于,,则,则 .
根据以上阅读理解,如图3、猜想(n等分时,内部有个点)(用n的代数式表示) .
2.(2024七下·唐山期中)平面直角坐标系中,点A的坐标为,将点A沿水平方向向右平移2个单位长度得到点B,则点B的坐标为 ,又将点B向下平移5个单位长度点C,则点C的坐标为 .
3.(2024七下·石家庄期中)如图,已知,,则 度.
4.(2024七下·保定期中)已知则 .
5.(2024七下·石家庄期中)如图,AD是△ABC的中线,点E为AD的中点,点F为BE的中点,S△ABC=41,则S△BFC= .
6.(2024七下·石家庄期中)(1)计算: .
(2)计算: .
7.(2024七下·石家庄期中)已知是关于x,y的二元一次方程,则 .
8.(2024七下·石家庄期中)已知,则 .
9.(2024七下·石家庄期中)计算
(1) .
(2) .
10.(2024七下·保定期中)如图,△ABC≌△A'B'C',其中∠A=36°,∠C'=24°,则∠B= 度.
11.(2024七下·东光期中)已知二元一次方程x﹣2y﹣1=0,若用含x的代数式表示y,可得 y= .
12.(2024七下·定州期中)在平面直角坐标系中,线段CD是由线段AB平移得到的,点的对应点,则点的对应点D的坐标为 .
13.(2024七下·柯桥期中)如果(x+3)(x+a)=x2﹣2x﹣15,则a= .
14.(2024七下·石家庄期中)如图,已知,则 ,则等于 (用含的式子表示).
15.(2024七下·石家庄期中)已知:如图,直线,,若,则 .
16.(2024七下·石家庄期中)把命题“两直线平行,同旁内角互补”改写成如果 ,那么 .
17.(2024七下·慈溪期中)如图,将直角三角形ABC沿AB方向平移4个单位长度得到三角形DEF,CG=3,EF=7,则图中阴影部分的面积为 .
18.(2024七下·丛台期中)如图,直线,点在上,点在上,点在之间,和的角平分线相交于点的角平分线交的反向延长线于点,下列四个结论:
①;
②;
③若,则;
④.
其中正确的结论是 (填写序号).
19.(2024七下·桥西期中)如图,已知,,则的度数为 .
20.(2024七下·桥西期中) .
21.(2024七下·竞秀期中)在,,三个内角中最大内角的度数为 ,的形状为 .
22.(2024七下·威县期中)如图,将长方形纸片ABCD沿直线EF折叠.若∠DFE=40°,则 .
23.(2024七下·新会期中)如果方程组的解与方程组的解相同,则a+b= .
24.(2024七下·石家庄期中)甲乙两位同学对问题“若关于x,y的方程组的解是,求方程组的解”提出各自的想法.甲说:“这个题目好像条件不够,不能求解”;乙说:“它们的系数有一定的规律,可以通过换元替代的方法来解决”
(1)你认为谁说得对? (填甲或乙);
(2)这个题目的解应该是 .
25.(2024七下·石家庄期中)若则 .
26.(2021七下·宣化期中)若∠A与∠B的两边分别平行,且∠A比∠B的3倍少40°,则∠B= 度.
27.(2024七下·宁海期中)因式分解:2x3﹣8x=
28.(2024七下·桥西期中)如图,在中,,,,E为AB上一动点,的最小值为2.4,过点B作,且,连接、,则的面积为 .
29.(2024七下·石家庄期中)当三角形中一个内角是另外一个内角的一半时,我们称此三角形为“友好三角形”.如果一个“友好三角形”中有一个内角为,那么这个“友好三角形”的“友好角”的度数为 .
30.(2024七下·石家庄期中)已知,用含的代数式表示可得 .
31.(2024七下·石家庄期中)如图,点分别在线段上,连接.若,则的度数为 .
32.(2024七下·定州期中)如图,是一块直角三角板,其中,直尺的一边DE经过顶点A,若,则∠DAB的度数为 度.
33.(2024七下·定州期中)如图,将三角形ABC沿BC方向平移3cm得到三角形DEF,若三角形ABC的周长为24cm,则四边形ABFD的周长为 cm.
34.(2024七下·石家庄期中)(1)光速约为米秒,太阳光射到地球上的时间约为秒,求地球与太阳的距离,用科学记数法表示为 米.
(2)某种病毒的长度为,这个数据用科学记数法表示为 .
35.(2024七下·任泽期中)已知关于的方程组
(1)若方程组的解满足,则 .
(2)若方程组的解中恰为整数,也为整数, .
36.(2024七下·昌黎期中)成人体内成熟的红细胞的平均直径一般为m,可以用科学记数法表示为 m.
37.(2024七下·石家庄期中)如图,,,交于点E.
(1)如图1,若于点D,,则的度数为 °;
(2)如图2,与的平分线交于点P,若,求的 °.
38.(2024七下·丰润期中)已知关于x,y的二元一次方程组的解满足,则k的值为 .
39.(2024七下·保定期中)如图,D、E分别是△ABC边AB、BC上的点,AD=2BD,BE=CE,设△ADF的面积为,△FCE的面积为,若S△ABC=24,则-的值为 .
40.(2024七下·襄都期中)如图,这是某校劳动实践基地的两块边长分别为的正方形用地,,其中种菜,种花,不能使用的部分(阴影部分)为,面积为.
(1)种菜和花的总面积为 (用含的代数式表示).
(2)经测量,与之和为8米,种菜的面积比种花的面积多了16平方米,则比长 米.
41.(2024七下·保定期中)如图,一块含30°角的直角三角尺,两个顶点分别在直尺的一对平行边上,若∠=110°,则∠= °.
42.(2024七下·桥西期中)如图,已知,,则的度数为 .
43.(2024七下·东光期中)如图,甲所示三角形纸片中,,将纸片沿过点B的直线折叠,使点C落到边上的E点处,折痕为(如图乙).再将纸片沿过点E的直线折叠,点A恰好与点D重合,折痕为(如图丙),则的大小为 .
44.(2024七下·保定期中)如图,从边长为的正方形纸片中剪去一个边长为的正方形,剩余部分沿虚线又剪拼成一个矩形(不重叠无缝隙),则矩形的面积为 .
45.(2023七下·孝南期中)把命题“相等的角是对顶角”改写成“如果…,那么…”的形式是
46.(2024七下·保定期中)如图,在中,点,点分别是,的中点,若的面积为1,则的面积为 .
47.(2024七下·献县期中)如图,直线,相交于点,过点作,射线平分,,则的度数为 ,的度数为 .
48.(2024七下·竞秀期中)如图,已知,点是上一点,交于点.
(1)与CF的位置关系是;
(2)若,,则的长为.
49.(2024七下·竞秀期中)若,则.
50.(2024七下·竞秀期中)如图,在中,为的中点,连接,取的中点,连接若的面积是1,则的面积是.
答案解析部分
1.;
2.;
3.
4.2
解:,
∴2m+3=7,
解得:m=2,
故答案为:2.
利用同底数幂的乘方及幂的乘方的计算方法可得,即可得到2m+3=7,最后求出m的值即可.
5..
6.;
7.
8.40
9.;
10.120
11.
12.
∵线段CD是由线段AB平移得到的,点的对应点,
∴线段CD是由线段AB先向右平移4个单位长度,再向上平移3个单位长度得到,
∵点B的坐标为(-4,-1),
∴点D的坐标为(-4+4,-1+3),即(0,2),
故答案为(0,2).
先利用点A、C的坐标证出线段CD是由线段AB先向右平移4个单位长度,再向上平移3个单位长度得到,再结合点B的坐标求出点D的坐标即可.
13.﹣5
解:(x+3)(x+a)=x2+(a+3)x+3a=x2﹣2x﹣15,
可得:a+3=﹣2,
解得:a=﹣5.
故答案为:﹣5.
已知等式左边利用多项式乘多项式法则计算,合并后利用多项式相等的条件即可求出a的值.
14.;
15.
16.两直线平行;同旁内角互补
17.22
解:∵Rt△ABC沿AB的方向平移AD距离得△DEF,
∴△DEF≌△ABC,
∴EF=BC=7,S△DEF=S△ABC,
∴S△ABC﹣S△DBG=S△DEF﹣S△DBG,
∴S四边形ACGD=S梯形BEFG,
∵CG=3,
∴BG=BC﹣CG=7﹣3=4,
∴S梯形BEFG (BG+EF) BE (4+7)×4=22.
故答案为:22.
根据平移的性质可得△DEF≌△ABC,即得S△DEF=S△ABC,从而求出S四边形ACGD=S梯形BEFG,根据梯形的面积公式计算即可.
18.①②④
19.70
解:如图所示:
∵a//b,∠1=110°,
∴∠3=∠1=110°,
∴∠2=180°-∠3=70°,
故答案为:70°.
利用平行线的性质可得∠3=∠1=110°,再利用邻补角求出∠2=180°-∠3=70°即可.
20.1
解:,
故答案为:1.
利用0指数幂的性质及计算方法分析求解即可.
21.;钝角三角形
22.100°
解:∵四边形ABCD是长方形,
∴DC∥AB.
∴∠DFE=∠FEB=40°.
∵折叠,
∴∠B1EF=∠FEB=40°.
∴∠AEB1=180°-∠FEB-∠B1EF=180°-40°-40°=100°.
故答案为:100°.
解题关键是结合平行线的性质与折叠的性质,解出∠FEB的度数和∠B1EF=∠FEB.
23.1
解:依题意,知是方程组的解,
①+②,得7a+7b=7,
方程两边都除以7,得a+b=1.
两个方程组的解相同,意思是这两个方程组中的x都等于4,y都等于3,即是方程组的解,根据方程组的解的定义,即可求出a+b的值.
24.乙;
25.
26.55或20
解:∵∠A与∠B的两边分别平行,
∴∠A+∠B=180°①,∠A=∠B②,
∵∠A比∠B的3倍少40°,
∴∠A=3∠B﹣40°③,
把③代入①得:3∠B﹣40°+∠B=180°,
∠B=55°,
把③代入②得:3∠B﹣40°=∠B,
∠B=20°,
故答案为:55或20.
根据题意当∠A与∠B的两边分别平行时,分为两种情况:∠A+∠B=180°,∠A=∠B,分别与∠A=3∠B﹣40°组成方程组,求解即可。
27. 2x(x+2)(x﹣2)
解:2x3﹣8x=2x(x2﹣4)=2x(x+2)(x﹣2).
故答案为:2x(x+2)(x﹣2).
先提公因式2x,分解成2x(x2﹣4),而x2﹣4可利用平方差公式分解.
28.14
29.或或
解:根据题意可得:,
①当时,,
解得:,
②当时,“友好角a”的度数为,
③当,时,
,
即,
解得:
综上:“友好角a”的度数为或或,
故答案为:或或.
分三种情况:①当时 ,②当时,③当,时,分别根据三角形内角和定理建立方程求解.
30.
解:∵,
∴,
∴,
故答案为:.
移项,化系数为1,据此求解.
31.
解:∵∠1=∠2=180° (∠B+∠ADB),∠ADB=∠A+∠C,
又∵,,,
∴∠1=180° (∠B+∠A+∠C)
=180° (25°+35°+50°)
=180° 110°
=70°
故答案为:70°.
由三角形的内角和定理,可得∠1=∠2=180 (∠B+∠ADB),根据外角的性质可得∠ADB=∠A+∠C,所以∠1=180° (∠B+∠A+∠C),由此解答即可.
32.120
∵,,
∴∠DAC=∠C=90°,
∵,
∴∠DAB=∠DAC+∠BAC=90°+30°=120°,
故答案为:120.
利用平行线的性质可得∠DAC=∠C=90°,再利用角的运算求出∠DAB=∠DAC+∠BAC=90°+30°=120°即可.
33.30
∵将三角形ABC沿BC方向平移3cm得到三角形DEF,且三角形ABC的周长为24cm,
∴AD=CF=3cm,AB+BC+AC=AB+BC+DF=24cm,
∴C四边形ABFD=AB+BC+DF+AD+CF=24+3+3=30cm,
故答案为:30.
利用平移的性质可得AD=CF=3cm,AB+BC+AC=AB+BC+DF=24cm,再利用四边形的周长公式及等量代换求解即可.
34.;
35.;或
36.
37.25;55
38.4
39.4
解:∵AD=2BD,
∴S△CBD= 13S△ABC=13×24=8 , ∵BE=CE,
∴S△ABE=,
∴S△ABE-S△CBD=(S1+S四边形BDFE)-(S2+S四边形BDFE)=S1-S2=12-8=4。
故答案为:4.
首先根据等高三角形面积之间的关系,求得S△CBD= 13S△ABC=13×24=8 ,S△ABE=,进而得出S△ABE-S△CBD=(S1+S四边形BDFE)-(S2+S四边形BDFE)=S1-S2=12-8=4。
40.;2
41.50
解:∵直尺的对边平行,
∴∠1=180°-α=180°-110°=70°,
∵∠2=60°,
∴∠β=180°-70°-60°=50°。
故答案为:50.
首先根据平行线的性质得出∠1=180°-α=180°-110°=70°,再根据平角的定义即可得出∠β=180°-70°-60°=50°。
42.70
43.120
44.
45.如果两个角是对顶角,那么两个角相等
解:∵原命题的条件是:“两个角是对顶角”,结论是:“这两个角相等”,
∴命题“对顶角相等”写成“如果…那么…”的形式为:“如果两个角是对顶角,那么两个角相等”,
故答案为:如果两个角是对顶角,那么两个角相等.
对顶角相等的条件是两个角是对顶角,结论是两角相等,据此即可改写成“如果…,那么…”的形式.
46.4
解:∵点E是AB的中点,的面积为1,
∴S△ADE=S△BDE=1,
∴S△ABD=S△ADE+S△BDE=1+1=2,
∵点D是BC的中点,
∴S△ADC=S△ABD=2,
∴S△ABC=S△ADC+S△ABD=2+2=4,
故答案为:4.
利用三角形中线平分三角形的面积可得S△ADE=S△BDE=1,S△ADC=S△ABD=2,再求出S△ABC=S△ADC+S△ABD=2+2=4即可.
47.;
48.,
49.27
50.
同课章节目录
