期中真题专项复习04 解答题(含答案)--2024-2025学年八年级数学下册(青岛版)
文档属性
| 名称 | 期中真题专项复习04 解答题(含答案)--2024-2025学年八年级数学下册(青岛版) |

|
|
| 格式 | docx | ||
| 文件大小 | 474.2KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-03-30 11:39:17 | ||
图片预览



文档简介
2024-2025学年八年级数学下册(青岛版)
期中真题专项复习04 解答题
一、解答题
1.(2024八下·青岛期中)为庆祝伟大的中国共产党成立100周年,发扬红色传统,传承红色精神,某学校举行了主题为“学史明理,学史增信,学史崇德,学史力行”的党史知识竞赛,一共有25道题,满分100分,每一题答对得4分,答错扣1分,不答得0分.
(1)若某参赛同学只有一道题没有作答,最后他的总得分为86分,则该参赛同学一共答对了多少道题?
(2)若规定参赛者每道题都必须作答且总得分大于或等于90分才可以被评为“学党史小达人”,则参赛者至少需答对多少道题才能被评为“学党史小达人”?
2.(2024八下·淄博期中)如图,正比例函数的图象与一次函数的图象交于点,一次函数的图象经过点,与y轴的交点为D,与x轴的交点为C.
(1)求一次函数的表达式;
(2)求的面积;
(3)不解关于的方程组,直接写出方程组的解.
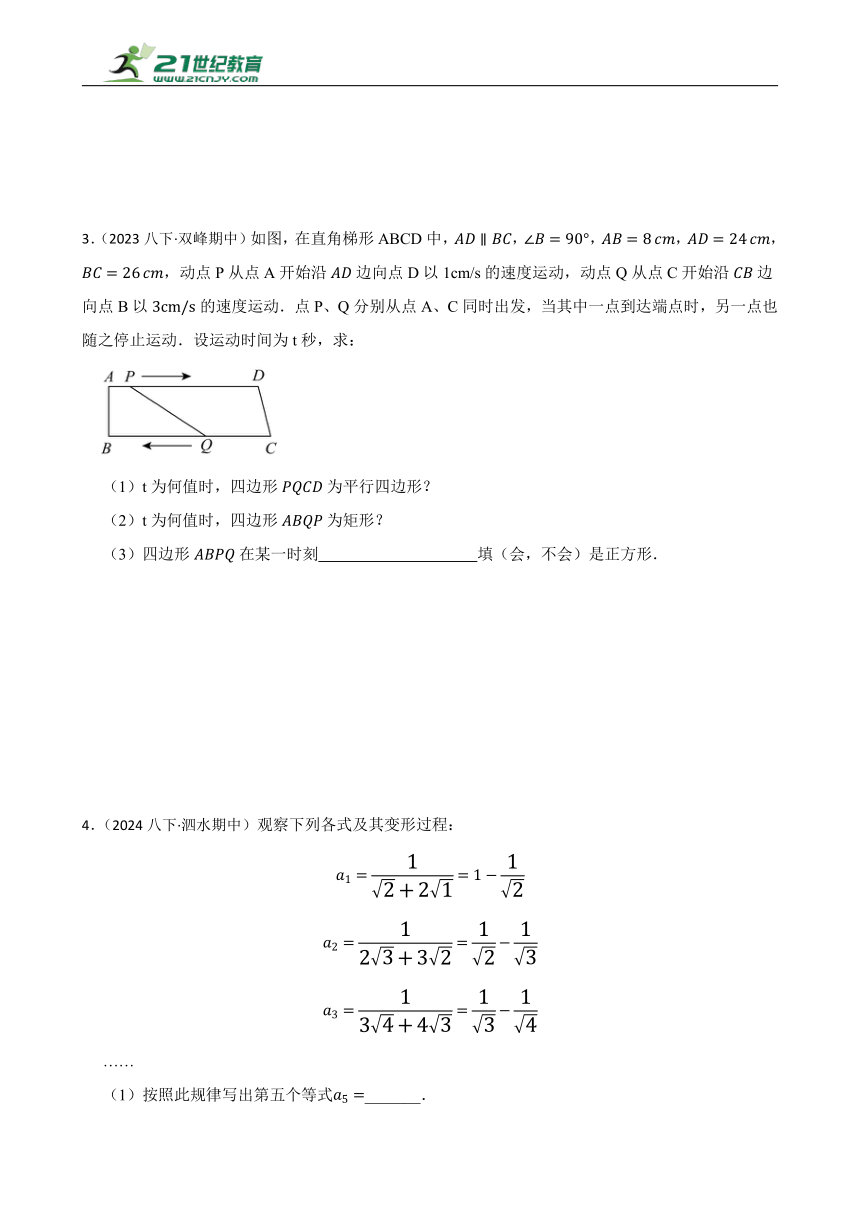
3.(2023八下·双峰期中)如图,在直角梯形ABCD中,,,,,,动点P从点A开始沿边向点D以1cm/s的速度运动,动点Q从点C开始沿边向点B以的速度运动.点P、Q分别从点A、C同时出发,当其中一点到达端点时,另一点也随之停止运动.设运动时间为t秒,求:
(1)t为何值时,四边形为平行四边形?
(2)t为何值时,四边形为矩形?
(3)四边形在某一时刻 填(会,不会)是正方形.
4.(2024八下·泗水期中)观察下列各式及其变形过程:
……
(1)按照此规律写出第五个等式_______.
(2)按照此规律,若,当时,_______.
(3)在(2)的条件下,若,试求的值.
5.(2024八下·庐江期中)在△ABC中,AB=15,BC=14,AC=13,求△ABC的面积.某学习小组经过合作交流,给出了下面的解题思路,请你按照他们的解题思路完成解答过程.作AD⊥BC于D,设BD=x,用含x的代数式表示CD→根据勾股定理,利用AD作为“桥梁”,建立方程模型求出x→利用勾股定理求出AD的长,再计算三角形的面积.
6.(2024八下·青岛期中)某公司准备把240吨白砂糖运往A、B两地,用大、小两种货车共20辆,恰好能一次性装完这批白砂糖,相关数据见表:
载重量 运往A地的费用 运往B地的费用
大车 15吨/辆 630元/辆 750元/辆
小车 10吨/辆 420元/辆 550元/辆
(1)求大、小两种货车各用多少辆?
(2)如果安排10辆货车前往A地,其中大车有m辆,其余货车前往B地,且运往A地的白砂糖不少于130吨.
①求m的取值范围;
②请设计出总运费最少的货车调配方案,并求最少总运费.
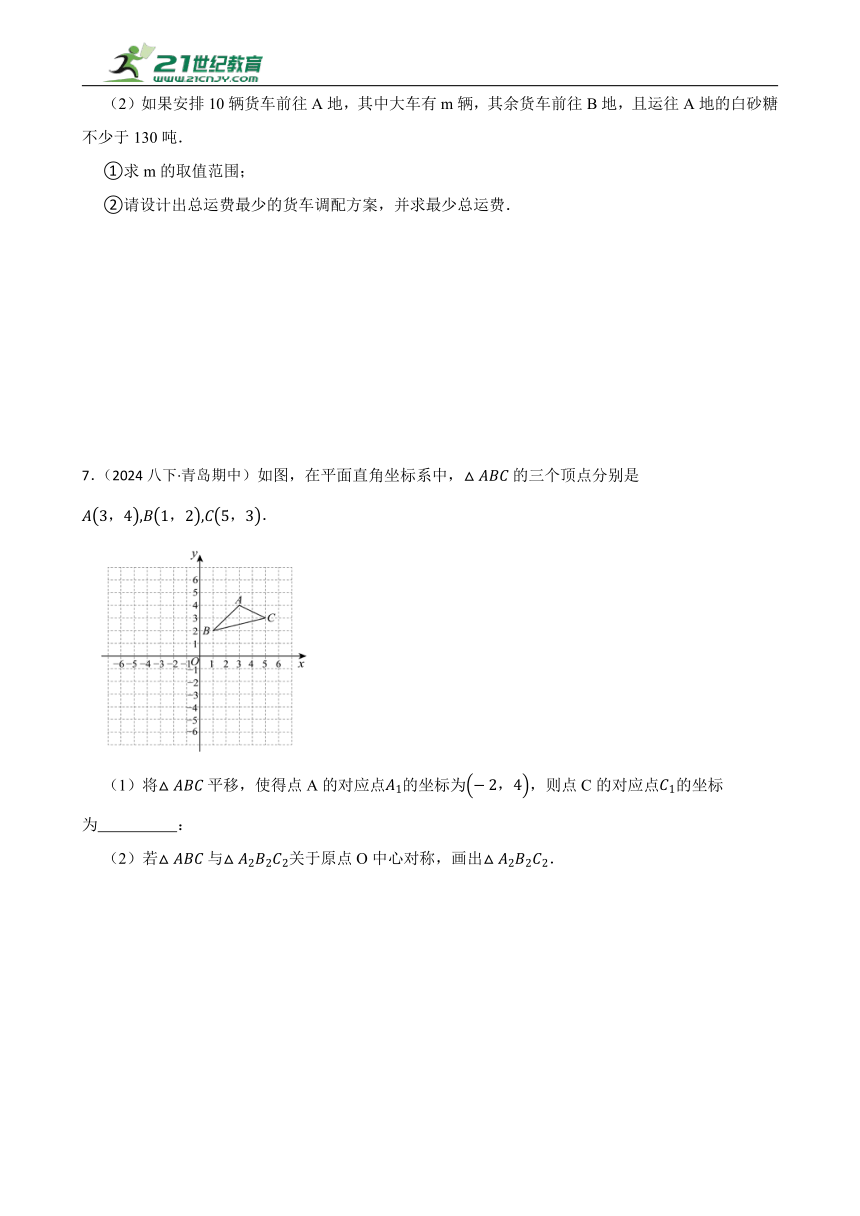
7.(2024八下·青岛期中)如图,在平面直角坐标系中,的三个顶点分别是.
(1)将平移,使得点A的对应点的坐标为,则点C的对应点的坐标为 :
(2)若与关于原点O中心对称,画出.
8.(2024八下·宁津期中)如图,四边形中,,过点A作于点E,E恰好是的中点,若.
(1)直接写出四边形的周长;
(2)求四边形的面积.
9.(2024八下·东港期中)无人机目前广泛应用于各个行业,在某地有A,,三个无人机起降点(三个起降点在同一水平面上),其中A在的北偏东54°方向上,与的距离是800米,在的南偏东36°方向上,与的距离是600米.
(1)求点A与点之间的距离;
(2)若在点的正上方高度为480米的空中有一个静止的信号源,信号覆盖半径为500米,每隔2秒会发射一次信号,此时在点的正上方同样高度处有一架无人机准备沿直线向点A飞行,无人机飞行的速度为每秒10米.
①若计划无人机在飞往A处的过程中维持高度不变,飞行到点A的正上方后再降落,试求无人机在飞行过程中,最多能收到多少次信号?(信号传播的时间忽略不计).
②无人机在按原计划飞行12秒后,因紧急情况需要飞到点处,请直接写出此时无人机飞到点需要的最短时间为______秒.
10.(2024八下·兰州期中)如图,已知函数=2x+b和=ax﹣3的图象交于点P(﹣2,﹣5),这两个函数的图象与x轴分别交于点A、B.
(1)分别求出这两个函数的解析式;
(2)求△ABP的面积;
(3)根据图象直接写出不等式2x+b<ax﹣3的解集.
11.(2024八下·岚山期中)阅读并回答下列问题.
几何模型:如图,、是直线同侧的两个定点.问题:在直线上找一点,使值最小.
方法:如图,作点关于的对称点,连接交于点,则为所求作的点.(不必说明)
模型应用:如图,若、两点在直线同侧,分别过点、作,,为线段上一动点,连接、.已知,,,设.
(1)用含的代数式表示的长为 ;
(2)拓展运用:
请问点满足什么条件时,的值最小,最小值为 ;
请问点满足什么条件时,的值最小,并求出最小值;
根据中的规律和结论,直接写出代数式的最小值.
12.(2024八下·济南期中)如图,在平行四边形中,,,.动点P从点A出发沿以速度向终点D运动,同时点Q从点C出发,以速度沿射线运动,当点P到达终点时,点Q也随之停止运动,设点P的运动时间为t秒().
(1)的长为 ;
(2)线段的长为 ;(用含t的代数式表示)
(3)当以P、Q、A、B为顶点的四边形为平行四边形时,求出t的值.
13.(2024八下·邹平期中)如图,直线的解析式为,且与轴交于点D,直线经过点A、B,直线、交于点C.
(1)求直线的解析表达式;
(2)求的面积;
(3)在直线上存在异于点C的另一点P,使得与的面积相等,请求出点P的坐标.
14.(2024八下·峄城期中)如图,Rt△ABC中,∠C=90°,AD平分∠BAC,交BC于点D,CD=1.5,BD=2.5.
(1)求点D到直线AB的距离;
(2)求线段AC的长.
15.(2024八下·腾冲期中)如图,已知某开发区有一块四边形空地ABCD,现计划在该空地上种植草皮,经测量∠ADC=90°,CD=6m,AD=8m,BC=24m,AB=26m,若每平方米草皮需200元,则在该空地上种植草皮共需多少钱?
16.(2024八下·芝罘期中)如图,中,D、E、F分别在、和上,,,若,,,求和的长度.
17.(2024八下·广饶期中)已知直角三角形的两条直角边分别是、,斜边是,
(1)如果,,求;
(2)如果,,求及直角三角形的面积.
18.(2024八下·济南期中) 如图, ABCD中,E、F为对角线BD上的两点,且DF=BE,连接AE,CF.
(1)求证:∠DAE=∠BCF.
(2)连接AF、CE,求证:四边形AECF是平行四边形.
19.(2024八下·德城期中)如图,方格纸中小正方形的边长为1,△ABC的三个顶点都在小正方形格点上,
(1)边AC、AB、BC的长;
(2)求△ABC的面积;
(3)点C到AB边的距离
20.(2024八下·李沧期中)【定义新知】
给定两个不等式P和Q,若不等式P的任意一个解,都是不等式Q的一个解,则称不等式P为不等式Q的“子集”.
例如:不等式P:是Q:的子集.
同理,给定两个不等式组M和N,若不等式组M的任意一个解,都是不等式组N的一个解,则称不等式组M为不等式组N的“子集”.
例如:不等式组M:是不等式组N:的子集.
【新知应用】
(1)请写出不等式的一个子集 ;
(2)若不等式组A:,不等式组B:,则其中不等式组 是不等式组M:的“子集”(填:A或B);
(3)若关于x的不等式组是不等式组的“子集”,则a的取值范围是 ;
(4)若a,b,c,d为互不相等的整数,,,下列三个不等式组D:,E:,F:,满足:D是E的“子集”且E是F的“子集”,则的值为 ;
(5)已知不等式组G:有解,且不等式组H:是不等式组G的“子集”,且m,n为正整数,则的最大值为 .
21.(2024八下·惠民期中)如图,一个直径为12cm的杯子,在它的正中间竖直放一根筷子,筷子漏出杯子外2cm,当筷子倒向杯壁时(筷子底端不动),筷子顶端正好触到杯口,求筷子长度.
22.(2024八下·潍城期中)在中,,点M为边的中点,点D在边上.
(1)若(如图①),求的长;
(2)过点M作与边所在的直线交于点E(如图②),试探究:线段、、三者之间的数量关系,并证明你的结论.
23.(2024八下·周村期中)实数与满足.
(1)写出与的取值范围;
(2)已知是有理数.
①当是正整数时,求的值;
②当是整数时,将符合条件的的值从大到小排列,请直接写出排在第3个位置和第11个位置的数.
24.(2024八下·宁阳期中)已知关于x的一元二次方程的两个根为a,b.
(1)若a,b分别是菱形的两条对角线的长,且菱形的面积为5,求m的值;
(2)若a,b分别为矩形的两条对角线的长,求m的值.
25.(2024八下·河东期中)在数学学习中,小明遇到一道题:已知,求的值.小明是这样解答的:∵,.请你根据小明的解题过程,解决下列问题:
(1)填空:_______,_______;
(2)化简:.
26.(2024八下·滨城期中)如图,在中,,,,将折叠,使点与的中点重合,折痕为,求线段的长.
27.(2024八下·济南期中)如图,在中,,将沿射线方向平移得到,点A、B、C的对应点分别是点D、E、F.
(1)若,求的度数.
(2)若,在平移过程中,当时,求的长.
28.(2024八下·兰陵期中)“为了安全,请勿超速”,如图所示是一条已经建成并通车的公路,且该公路的某直线路段MN上限速17m/s,为了检测来往车辆是否超速,交警在MN旁设立了观测点C.若某次从观测点C测得一汽车从点A到达点B行驶了5秒钟,已知∠CAN=45°,∠CBN=60°,BC=200m.
(1)求观测点C到公路MN的距离;
(2)请你判断该汽车是否超速?(参考数据:≈1.41,≈1.73)
29.(2024八下·博山期中)如图,已知正方形点在边上,以为边在左侧作正方形;以为邻边作平行四边形连接.
(1)判断和的数量及位置关系,并说明理由;
(2)将绕点顺时针旋转,在旋转过程中,和的数量及位置关系是否发生变化?请说明理由.
30.(2024八下·博山期中)已知a=+1,b=﹣1,试求a2+2ab+b2的值.
答案解析部分
1.解:(1)设该参赛同学一共答对了道题,则该参赛同学一共答错了道题,
由题意得:,
解得,
答:该参赛同学一共答对了22道题;
(2)设参赛者需答对道题才能被评为“学党史小达人”,则参赛者答错了道题,
由题意得:,
解得,
答:参赛者至少需答对23道题才能被评为“学党史小达人”.
(1)设该参赛同学一共答对了道题,从而可得该参赛同学一共答错了道题,再根据“每一题答对得4分,答错扣1分,不答得0分”、“他的总得分为86分”建立方程,解方程即可求出答案.
(2)设参赛者需答对道题才能被评为“学党史小达人”,从而可得参赛者答错了道题,再根据“总得分大于或等于90分”建立不等式,解不等式即可求出答案.
2.(1)
(2)3
(3)
3.(1)当秒时,四边形为平行四边形
(2)当秒时,四边形为矩形
(3)不会
4.(1)
(2)
(3)
5.解:如图,
在△ABC中,AB=15,BC=14,AC=13,
设BD=x,则有CD=14﹣x,
由勾股定理得:AD2=AB2﹣BD2=152﹣x2,AD2=AC2﹣CD2=132﹣(14﹣x)2,
∴152﹣x2=132﹣(14﹣x)2,
解之得:x=9,
∴AD=12,
∴S△ABC=BC AD=×14×12=84.
设BD=x,则有CD=14﹣x,根据勾股定理可得152﹣x2=132﹣(14﹣x)2,再求出x的值,最后利用三角形的面积公式求解即可。
6.解:(1)设大货车x辆,则小货车有(20-x)辆,
15x+10(20-x)=240,
解得:x=8,
20-x=20-8=12(辆),
答:大货车用8辆.小货车用12辆;
(2)①调往A地的大车有m辆,则到A地的小车有(10-m)辆,由题意得:
15m+10(10-m)≥130,
解得:m≥6,
∵大车共有8辆,
∴6≤m≤8;
②设总运费为W元,
∵调往A地的大车有m辆,则到A地的小车有(10-m)辆,
∴到B的大车(8-m)辆,到B的小车有[12-(10-m)]=(2+m)辆,
W=630m+420(10-m)+750(8-m)+550(2+m),
=630m+4200-420m+6000-750m+1100+550m,
=10m+11300.
又∵W随m的增大而增大,
∴当m=6时,w最小.
当m=6时,W=10×6+11300=11360.
因此,应安排6辆大车和4辆小车前往A地,安排2辆大车和8辆小车前往B地,最少运费为11360元.
(1)设大车货x辆,则小货车(20-x)辆,根据“大车装的货物数量+小车装的货物数量=240吨”作为相等关系列方程,解方程即可求出答案.
(2)①调往A地的大车m辆,小车(10-m)辆;调往B地的大车(8-m)辆,小车(m+2)辆,根据“运往A地的白砂糖不少于130吨”列关于m的不等式求出m的取值范围,
②设总运费为W元,根据运费的求算方法列出关于运费的函数关系式W=10m+11300,再结合一次函数的单调性得出w的最小值即可求解.
7.(1)
(2)如图所示,即为所求.
(1)将平移,使得点的对应点的坐标为,
即将向左平移5个单位,,
如图所示,即为所求;
(1)将三个顶点分别向左平移5个单位,再首尾顺次连接即可得;
(2)分别作出三个顶点关于原点O中心对称的对称点,再首尾顺次连接即可得.
8.(1)
(2)
9.(1)点A与点之间的距离为1000米
(2)①无人机收到信号次数最多为次;②72
10.(1),;
(2)
(3)
11.(1);
(2)当时,最小值为;
当、、三点共线时取最小值,;
代数式最小值为.
12.(1)10
(2)或
(3)或1
13.(1)直线的解析表达式为
(2)
(3)点P的坐标为(6,3).
14.(1)1.5
(2)3
15.19200
16.,
17.(1)
(2),
18.(1)证明:∵四边形ABCD为平行四边形,
∴AB∥CD,AB=CD,
∴∠ABD=∠CDB,
在△ABE与△CDF中
,
∴△ABE≌△CDF(SAS),
∴∠DAE=∠BCF.
(2)证明:连接AO交BD于点O,连接AF、CE.
由(1)得,△ABE≌△CDF,
∴∠AED=∠CFB,AE=CF,
∴∠AEB=∠CFD,
∴AE∥CF,
∴四边形AECF为平行四边形.
(1)由“SAS”可证△ABE≌△CDF,即可推出∠DAE=∠BCF;
(2)由平行四边形的判定可证四边形AECF为平行四边形。熟练掌握全等三角形的判定和性质是解题的关键。
19.(1);(2);(3)
20.(1)(答案不唯一)
(2)A
(3)
(4)120
(5)
21.10cm
22.(1)解:连接,
在中,
∵,,
∴,
∵点为边的中点,,
∴是线段的垂直平分线,
∴,
设,则,
在中,
∵,即,
解得,即,
∵,
∴;
(2)解:.理由如下,
作交的延长线于点,连接,
∵
∴,,
∵点为边的中点,
∴,
∴,
∴,,
∵,
∴∠EMN=∠EMD,
又∵EM =EM ,
∴△EMN≌△EMD(SAS),
∴,
∵,,
∴,
∴△EAN为直角三角形,
∴,即.
(1)先利用勾股定理求出,再证明是线段的垂直平分线,再利用垂直平分线的性质和勾股定理,求出AD=BD=5,再利用等面积法即可求出MD的长;
(2)作交的延长线于点,证明,推出,,再证明△EMN≌△EMD(SAS),得到,再根据勾股定理即可得到结论.
(1)解:连接,
∵点为边的中点,,
∴是线段的垂直平分线,
∴,
设,则,
在中,由勾股定理,即,
解得,即,
在中,,,
∴,
∵,
∴;
(2)解:.理由如下,
作交的延长线于点,连接,
∴,,
∵点为边的中点,
∴,
∴,
∴,,
∵,
∴是线段的垂直平分线,
∴,
∵,,
∴,
∴,即.
23.(1)
(2)①或②
24.(1)7;
(2)6.
25.(1);
(2)
26.
27.(1)
(2)或
28.(1)100m;(2) 该汽车没有超速.
29.解:(1),.
由题意可得,平行四边形为矩形,,,,
,
,,
,
,
设与交于点,
则,
即.
(2)与的数量及位置关系都不变.
如图,延长到点,
四边形为平行四边形,
,,,
,
,,
,
,
,
又,,
,
,,
,
,
,
,
即.
(1)根据全等三角形判定定理可得,则,,再根据角之间的关系可得,设与交于点,则,即,即可求出答案.
(2)延长到点,根据平行四边形性质可得,,,则,再根据角之间的关系可得,由全等三角形判定定理可得,则,,再根据直线平行性质可得,再根据角之间的关系可得,则,即可求出答案.
30.解:∵a= +1,b=﹣1,
∴a2+2ab+b2
=(a+b)2
=(+1+﹣1)2
=(2)2
=20.
根据完全平方公式化简代数值,再将a,b值代入即可求出答案.
期中真题专项复习04 解答题
一、解答题
1.(2024八下·青岛期中)为庆祝伟大的中国共产党成立100周年,发扬红色传统,传承红色精神,某学校举行了主题为“学史明理,学史增信,学史崇德,学史力行”的党史知识竞赛,一共有25道题,满分100分,每一题答对得4分,答错扣1分,不答得0分.
(1)若某参赛同学只有一道题没有作答,最后他的总得分为86分,则该参赛同学一共答对了多少道题?
(2)若规定参赛者每道题都必须作答且总得分大于或等于90分才可以被评为“学党史小达人”,则参赛者至少需答对多少道题才能被评为“学党史小达人”?
2.(2024八下·淄博期中)如图,正比例函数的图象与一次函数的图象交于点,一次函数的图象经过点,与y轴的交点为D,与x轴的交点为C.
(1)求一次函数的表达式;
(2)求的面积;
(3)不解关于的方程组,直接写出方程组的解.
3.(2023八下·双峰期中)如图,在直角梯形ABCD中,,,,,,动点P从点A开始沿边向点D以1cm/s的速度运动,动点Q从点C开始沿边向点B以的速度运动.点P、Q分别从点A、C同时出发,当其中一点到达端点时,另一点也随之停止运动.设运动时间为t秒,求:
(1)t为何值时,四边形为平行四边形?
(2)t为何值时,四边形为矩形?
(3)四边形在某一时刻 填(会,不会)是正方形.
4.(2024八下·泗水期中)观察下列各式及其变形过程:
……
(1)按照此规律写出第五个等式_______.
(2)按照此规律,若,当时,_______.
(3)在(2)的条件下,若,试求的值.
5.(2024八下·庐江期中)在△ABC中,AB=15,BC=14,AC=13,求△ABC的面积.某学习小组经过合作交流,给出了下面的解题思路,请你按照他们的解题思路完成解答过程.作AD⊥BC于D,设BD=x,用含x的代数式表示CD→根据勾股定理,利用AD作为“桥梁”,建立方程模型求出x→利用勾股定理求出AD的长,再计算三角形的面积.
6.(2024八下·青岛期中)某公司准备把240吨白砂糖运往A、B两地,用大、小两种货车共20辆,恰好能一次性装完这批白砂糖,相关数据见表:
载重量 运往A地的费用 运往B地的费用
大车 15吨/辆 630元/辆 750元/辆
小车 10吨/辆 420元/辆 550元/辆
(1)求大、小两种货车各用多少辆?
(2)如果安排10辆货车前往A地,其中大车有m辆,其余货车前往B地,且运往A地的白砂糖不少于130吨.
①求m的取值范围;
②请设计出总运费最少的货车调配方案,并求最少总运费.
7.(2024八下·青岛期中)如图,在平面直角坐标系中,的三个顶点分别是.
(1)将平移,使得点A的对应点的坐标为,则点C的对应点的坐标为 :
(2)若与关于原点O中心对称,画出.
8.(2024八下·宁津期中)如图,四边形中,,过点A作于点E,E恰好是的中点,若.
(1)直接写出四边形的周长;
(2)求四边形的面积.
9.(2024八下·东港期中)无人机目前广泛应用于各个行业,在某地有A,,三个无人机起降点(三个起降点在同一水平面上),其中A在的北偏东54°方向上,与的距离是800米,在的南偏东36°方向上,与的距离是600米.
(1)求点A与点之间的距离;
(2)若在点的正上方高度为480米的空中有一个静止的信号源,信号覆盖半径为500米,每隔2秒会发射一次信号,此时在点的正上方同样高度处有一架无人机准备沿直线向点A飞行,无人机飞行的速度为每秒10米.
①若计划无人机在飞往A处的过程中维持高度不变,飞行到点A的正上方后再降落,试求无人机在飞行过程中,最多能收到多少次信号?(信号传播的时间忽略不计).
②无人机在按原计划飞行12秒后,因紧急情况需要飞到点处,请直接写出此时无人机飞到点需要的最短时间为______秒.
10.(2024八下·兰州期中)如图,已知函数=2x+b和=ax﹣3的图象交于点P(﹣2,﹣5),这两个函数的图象与x轴分别交于点A、B.
(1)分别求出这两个函数的解析式;
(2)求△ABP的面积;
(3)根据图象直接写出不等式2x+b<ax﹣3的解集.
11.(2024八下·岚山期中)阅读并回答下列问题.
几何模型:如图,、是直线同侧的两个定点.问题:在直线上找一点,使值最小.
方法:如图,作点关于的对称点,连接交于点,则为所求作的点.(不必说明)
模型应用:如图,若、两点在直线同侧,分别过点、作,,为线段上一动点,连接、.已知,,,设.
(1)用含的代数式表示的长为 ;
(2)拓展运用:
请问点满足什么条件时,的值最小,最小值为 ;
请问点满足什么条件时,的值最小,并求出最小值;
根据中的规律和结论,直接写出代数式的最小值.
12.(2024八下·济南期中)如图,在平行四边形中,,,.动点P从点A出发沿以速度向终点D运动,同时点Q从点C出发,以速度沿射线运动,当点P到达终点时,点Q也随之停止运动,设点P的运动时间为t秒().
(1)的长为 ;
(2)线段的长为 ;(用含t的代数式表示)
(3)当以P、Q、A、B为顶点的四边形为平行四边形时,求出t的值.
13.(2024八下·邹平期中)如图,直线的解析式为,且与轴交于点D,直线经过点A、B,直线、交于点C.
(1)求直线的解析表达式;
(2)求的面积;
(3)在直线上存在异于点C的另一点P,使得与的面积相等,请求出点P的坐标.
14.(2024八下·峄城期中)如图,Rt△ABC中,∠C=90°,AD平分∠BAC,交BC于点D,CD=1.5,BD=2.5.
(1)求点D到直线AB的距离;
(2)求线段AC的长.
15.(2024八下·腾冲期中)如图,已知某开发区有一块四边形空地ABCD,现计划在该空地上种植草皮,经测量∠ADC=90°,CD=6m,AD=8m,BC=24m,AB=26m,若每平方米草皮需200元,则在该空地上种植草皮共需多少钱?
16.(2024八下·芝罘期中)如图,中,D、E、F分别在、和上,,,若,,,求和的长度.
17.(2024八下·广饶期中)已知直角三角形的两条直角边分别是、,斜边是,
(1)如果,,求;
(2)如果,,求及直角三角形的面积.
18.(2024八下·济南期中) 如图, ABCD中,E、F为对角线BD上的两点,且DF=BE,连接AE,CF.
(1)求证:∠DAE=∠BCF.
(2)连接AF、CE,求证:四边形AECF是平行四边形.
19.(2024八下·德城期中)如图,方格纸中小正方形的边长为1,△ABC的三个顶点都在小正方形格点上,
(1)边AC、AB、BC的长;
(2)求△ABC的面积;
(3)点C到AB边的距离
20.(2024八下·李沧期中)【定义新知】
给定两个不等式P和Q,若不等式P的任意一个解,都是不等式Q的一个解,则称不等式P为不等式Q的“子集”.
例如:不等式P:是Q:的子集.
同理,给定两个不等式组M和N,若不等式组M的任意一个解,都是不等式组N的一个解,则称不等式组M为不等式组N的“子集”.
例如:不等式组M:是不等式组N:的子集.
【新知应用】
(1)请写出不等式的一个子集 ;
(2)若不等式组A:,不等式组B:,则其中不等式组 是不等式组M:的“子集”(填:A或B);
(3)若关于x的不等式组是不等式组的“子集”,则a的取值范围是 ;
(4)若a,b,c,d为互不相等的整数,,,下列三个不等式组D:,E:,F:,满足:D是E的“子集”且E是F的“子集”,则的值为 ;
(5)已知不等式组G:有解,且不等式组H:是不等式组G的“子集”,且m,n为正整数,则的最大值为 .
21.(2024八下·惠民期中)如图,一个直径为12cm的杯子,在它的正中间竖直放一根筷子,筷子漏出杯子外2cm,当筷子倒向杯壁时(筷子底端不动),筷子顶端正好触到杯口,求筷子长度.
22.(2024八下·潍城期中)在中,,点M为边的中点,点D在边上.
(1)若(如图①),求的长;
(2)过点M作与边所在的直线交于点E(如图②),试探究:线段、、三者之间的数量关系,并证明你的结论.
23.(2024八下·周村期中)实数与满足.
(1)写出与的取值范围;
(2)已知是有理数.
①当是正整数时,求的值;
②当是整数时,将符合条件的的值从大到小排列,请直接写出排在第3个位置和第11个位置的数.
24.(2024八下·宁阳期中)已知关于x的一元二次方程的两个根为a,b.
(1)若a,b分别是菱形的两条对角线的长,且菱形的面积为5,求m的值;
(2)若a,b分别为矩形的两条对角线的长,求m的值.
25.(2024八下·河东期中)在数学学习中,小明遇到一道题:已知,求的值.小明是这样解答的:∵,.请你根据小明的解题过程,解决下列问题:
(1)填空:_______,_______;
(2)化简:.
26.(2024八下·滨城期中)如图,在中,,,,将折叠,使点与的中点重合,折痕为,求线段的长.
27.(2024八下·济南期中)如图,在中,,将沿射线方向平移得到,点A、B、C的对应点分别是点D、E、F.
(1)若,求的度数.
(2)若,在平移过程中,当时,求的长.
28.(2024八下·兰陵期中)“为了安全,请勿超速”,如图所示是一条已经建成并通车的公路,且该公路的某直线路段MN上限速17m/s,为了检测来往车辆是否超速,交警在MN旁设立了观测点C.若某次从观测点C测得一汽车从点A到达点B行驶了5秒钟,已知∠CAN=45°,∠CBN=60°,BC=200m.
(1)求观测点C到公路MN的距离;
(2)请你判断该汽车是否超速?(参考数据:≈1.41,≈1.73)
29.(2024八下·博山期中)如图,已知正方形点在边上,以为边在左侧作正方形;以为邻边作平行四边形连接.
(1)判断和的数量及位置关系,并说明理由;
(2)将绕点顺时针旋转,在旋转过程中,和的数量及位置关系是否发生变化?请说明理由.
30.(2024八下·博山期中)已知a=+1,b=﹣1,试求a2+2ab+b2的值.
答案解析部分
1.解:(1)设该参赛同学一共答对了道题,则该参赛同学一共答错了道题,
由题意得:,
解得,
答:该参赛同学一共答对了22道题;
(2)设参赛者需答对道题才能被评为“学党史小达人”,则参赛者答错了道题,
由题意得:,
解得,
答:参赛者至少需答对23道题才能被评为“学党史小达人”.
(1)设该参赛同学一共答对了道题,从而可得该参赛同学一共答错了道题,再根据“每一题答对得4分,答错扣1分,不答得0分”、“他的总得分为86分”建立方程,解方程即可求出答案.
(2)设参赛者需答对道题才能被评为“学党史小达人”,从而可得参赛者答错了道题,再根据“总得分大于或等于90分”建立不等式,解不等式即可求出答案.
2.(1)
(2)3
(3)
3.(1)当秒时,四边形为平行四边形
(2)当秒时,四边形为矩形
(3)不会
4.(1)
(2)
(3)
5.解:如图,
在△ABC中,AB=15,BC=14,AC=13,
设BD=x,则有CD=14﹣x,
由勾股定理得:AD2=AB2﹣BD2=152﹣x2,AD2=AC2﹣CD2=132﹣(14﹣x)2,
∴152﹣x2=132﹣(14﹣x)2,
解之得:x=9,
∴AD=12,
∴S△ABC=BC AD=×14×12=84.
设BD=x,则有CD=14﹣x,根据勾股定理可得152﹣x2=132﹣(14﹣x)2,再求出x的值,最后利用三角形的面积公式求解即可。
6.解:(1)设大货车x辆,则小货车有(20-x)辆,
15x+10(20-x)=240,
解得:x=8,
20-x=20-8=12(辆),
答:大货车用8辆.小货车用12辆;
(2)①调往A地的大车有m辆,则到A地的小车有(10-m)辆,由题意得:
15m+10(10-m)≥130,
解得:m≥6,
∵大车共有8辆,
∴6≤m≤8;
②设总运费为W元,
∵调往A地的大车有m辆,则到A地的小车有(10-m)辆,
∴到B的大车(8-m)辆,到B的小车有[12-(10-m)]=(2+m)辆,
W=630m+420(10-m)+750(8-m)+550(2+m),
=630m+4200-420m+6000-750m+1100+550m,
=10m+11300.
又∵W随m的增大而增大,
∴当m=6时,w最小.
当m=6时,W=10×6+11300=11360.
因此,应安排6辆大车和4辆小车前往A地,安排2辆大车和8辆小车前往B地,最少运费为11360元.
(1)设大车货x辆,则小货车(20-x)辆,根据“大车装的货物数量+小车装的货物数量=240吨”作为相等关系列方程,解方程即可求出答案.
(2)①调往A地的大车m辆,小车(10-m)辆;调往B地的大车(8-m)辆,小车(m+2)辆,根据“运往A地的白砂糖不少于130吨”列关于m的不等式求出m的取值范围,
②设总运费为W元,根据运费的求算方法列出关于运费的函数关系式W=10m+11300,再结合一次函数的单调性得出w的最小值即可求解.
7.(1)
(2)如图所示,即为所求.
(1)将平移,使得点的对应点的坐标为,
即将向左平移5个单位,,
如图所示,即为所求;
(1)将三个顶点分别向左平移5个单位,再首尾顺次连接即可得;
(2)分别作出三个顶点关于原点O中心对称的对称点,再首尾顺次连接即可得.
8.(1)
(2)
9.(1)点A与点之间的距离为1000米
(2)①无人机收到信号次数最多为次;②72
10.(1),;
(2)
(3)
11.(1);
(2)当时,最小值为;
当、、三点共线时取最小值,;
代数式最小值为.
12.(1)10
(2)或
(3)或1
13.(1)直线的解析表达式为
(2)
(3)点P的坐标为(6,3).
14.(1)1.5
(2)3
15.19200
16.,
17.(1)
(2),
18.(1)证明:∵四边形ABCD为平行四边形,
∴AB∥CD,AB=CD,
∴∠ABD=∠CDB,
在△ABE与△CDF中
,
∴△ABE≌△CDF(SAS),
∴∠DAE=∠BCF.
(2)证明:连接AO交BD于点O,连接AF、CE.
由(1)得,△ABE≌△CDF,
∴∠AED=∠CFB,AE=CF,
∴∠AEB=∠CFD,
∴AE∥CF,
∴四边形AECF为平行四边形.
(1)由“SAS”可证△ABE≌△CDF,即可推出∠DAE=∠BCF;
(2)由平行四边形的判定可证四边形AECF为平行四边形。熟练掌握全等三角形的判定和性质是解题的关键。
19.(1);(2);(3)
20.(1)(答案不唯一)
(2)A
(3)
(4)120
(5)
21.10cm
22.(1)解:连接,
在中,
∵,,
∴,
∵点为边的中点,,
∴是线段的垂直平分线,
∴,
设,则,
在中,
∵,即,
解得,即,
∵,
∴;
(2)解:.理由如下,
作交的延长线于点,连接,
∵
∴,,
∵点为边的中点,
∴,
∴,
∴,,
∵,
∴∠EMN=∠EMD,
又∵EM =EM ,
∴△EMN≌△EMD(SAS),
∴,
∵,,
∴,
∴△EAN为直角三角形,
∴,即.
(1)先利用勾股定理求出,再证明是线段的垂直平分线,再利用垂直平分线的性质和勾股定理,求出AD=BD=5,再利用等面积法即可求出MD的长;
(2)作交的延长线于点,证明,推出,,再证明△EMN≌△EMD(SAS),得到,再根据勾股定理即可得到结论.
(1)解:连接,
∵点为边的中点,,
∴是线段的垂直平分线,
∴,
设,则,
在中,由勾股定理,即,
解得,即,
在中,,,
∴,
∵,
∴;
(2)解:.理由如下,
作交的延长线于点,连接,
∴,,
∵点为边的中点,
∴,
∴,
∴,,
∵,
∴是线段的垂直平分线,
∴,
∵,,
∴,
∴,即.
23.(1)
(2)①或②
24.(1)7;
(2)6.
25.(1);
(2)
26.
27.(1)
(2)或
28.(1)100m;(2) 该汽车没有超速.
29.解:(1),.
由题意可得,平行四边形为矩形,,,,
,
,,
,
,
设与交于点,
则,
即.
(2)与的数量及位置关系都不变.
如图,延长到点,
四边形为平行四边形,
,,,
,
,,
,
,
,
又,,
,
,,
,
,
,
,
即.
(1)根据全等三角形判定定理可得,则,,再根据角之间的关系可得,设与交于点,则,即,即可求出答案.
(2)延长到点,根据平行四边形性质可得,,,则,再根据角之间的关系可得,由全等三角形判定定理可得,则,,再根据直线平行性质可得,再根据角之间的关系可得,则,即可求出答案.
30.解:∵a= +1,b=﹣1,
∴a2+2ab+b2
=(a+b)2
=(+1+﹣1)2
=(2)2
=20.
根据完全平方公式化简代数值,再将a,b值代入即可求出答案.
同课章节目录
