期中真题专项复习01 选择题(含答案)--2024-2025学年八年级数学下册(青岛版)
文档属性
| 名称 | 期中真题专项复习01 选择题(含答案)--2024-2025学年八年级数学下册(青岛版) |  | |
| 格式 | docx | ||
| 文件大小 | 521.4KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-03-30 13:13:51 | ||
图片预览


文档简介
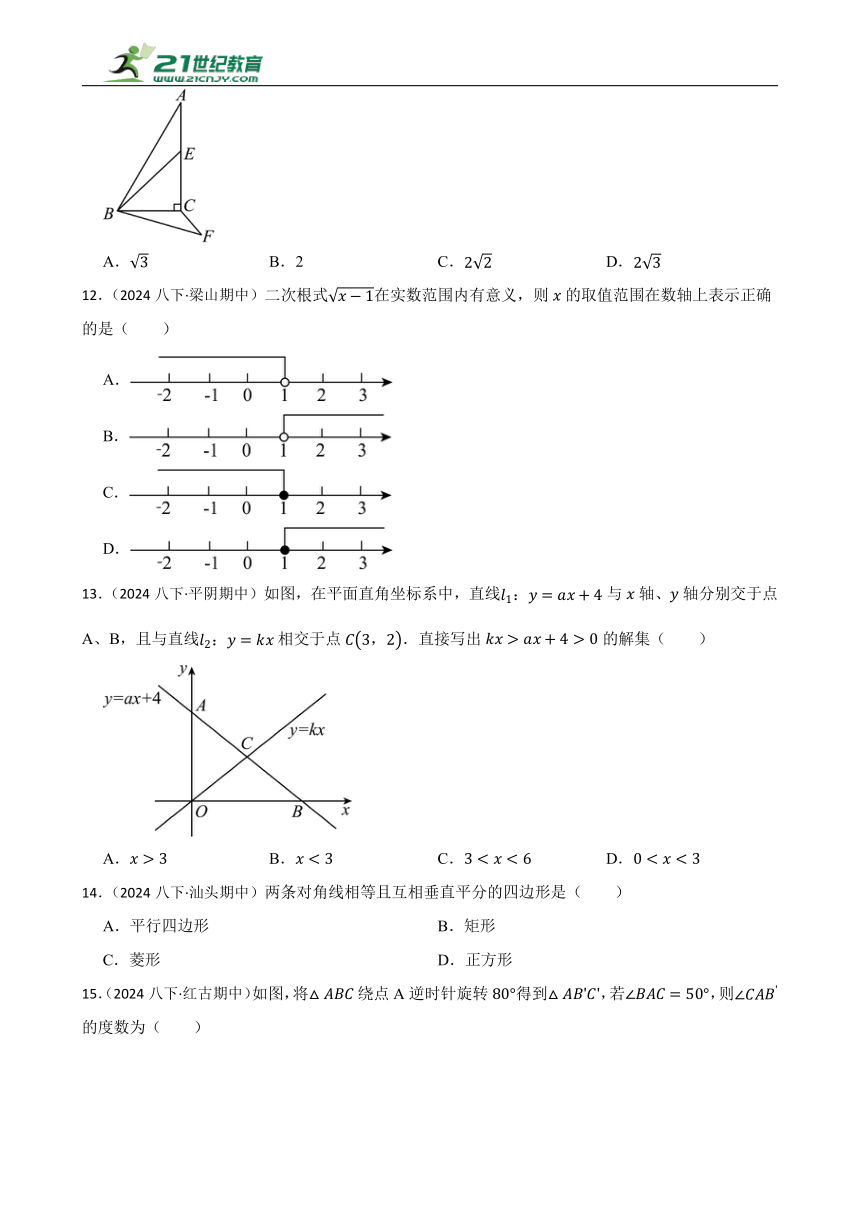
2024-2025学年八年级数学下册(青岛版)
期中真题专项复习01 选择题
一、选择题
1.(2024八下·青岛期中)若,则下列不等式一定成立的是( )
A. B. C. D.
2.(2024八下·潍坊期中)若的小数部分是a,则的值为( )
A.1 B. C.3 D.12
3.(2024八下·淄博期中)如图,在正方形中,F是边上的一点,连结并延长与的延长线相交于点E.若,则的值为( )
A. B. C. D.
4.(2024八下·聊城期中)若关于x的不等式组无解,则实数m的取值范围是( )
A. B. C. D.
5.(2024八下·聊城期中)下列实数中的无理数是( )
A. B.0 C. D.
6.(2022八下·港北期中)如图,在中,分别是的中点,点在延长线上,添加一个条件使四边形为平行四边形,则这个条件是( )
A. B. C. D.
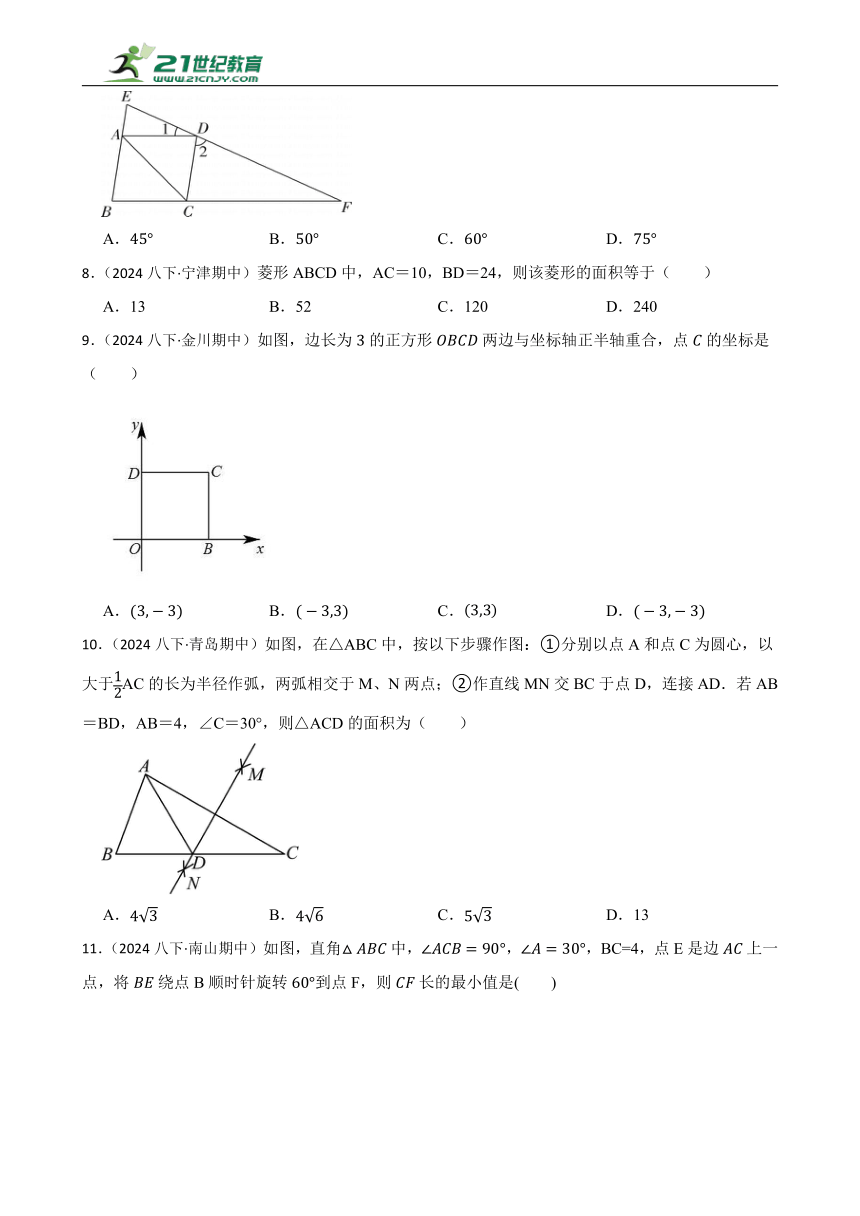
7.(2024八下·徐闻期中)如图,四边形是菱形,过点的直线分别交,的延长线于点,,若,,则等于( )
A. B. C. D.
8.(2024八下·宁津期中)菱形ABCD中,AC=10,BD=24,则该菱形的面积等于( )
A.13 B.52 C.120 D.240
9.(2024八下·金川期中)如图,边长为的正方形两边与坐标轴正半轴重合,点的坐标是( )
A. B. C. D.
10.(2024八下·青岛期中)如图,在△ABC中,按以下步骤作图:①分别以点A和点C为圆心,以大于AC的长为半径作弧,两弧相交于M、N两点;②作直线MN交BC于点D,连接AD.若AB=BD,AB=4,∠C=30°,则△ACD的面积为( )
A. B. C. D.13
11.(2024八下·南山期中)如图,直角中,,,BC=4,点E是边上一点,将绕点B顺时针旋转到点F,则长的最小值是( )
A. B.2 C. D.
12.(2024八下·梁山期中)二次根式在实数范围内有意义,则的取值范围在数轴上表示正确的是( )
A.
B.
C.
D.
13.(2024八下·平阴期中)如图,在平面直角坐标系中,直线与轴、轴分别交于点A、B,且与直线相交于点.直接写出的解集( )
A. B. C. D.
14.(2024八下·汕头期中)两条对角线相等且互相垂直平分的四边形是( )
A.平行四边形 B.矩形
C.菱形 D.正方形
15.(2024八下·红古期中)如图,将绕点A逆时针旋转得到,若,则的度数为( )
A. B. C. D..
16.(2022八下·曲阳期中)函数的自变量的取值范围是( )
A.x>0且x≠ B.x≥0且x≠ C.x≥0 D.x≠
17.(2024八下·宁津期中)下列二次根式中,最简二次根式是( )
A. B. C. D.
18.(2024八下·杭州期中)如图,四边形ABCD是平行四边形,O是对角线AC与BD的交点,AB⊥AC,若AB=8,AC=12,则BD的长是( )
A.16 B.18 C.20 D.22
19.(2024八下·邳州期中)如图,正方形ABCD和正方形CEFG中,点D在CG上,已知BC=1,CE=7,点H是AF的中点,则CH的长是( )
A.5 B.3.5 C.4 D.
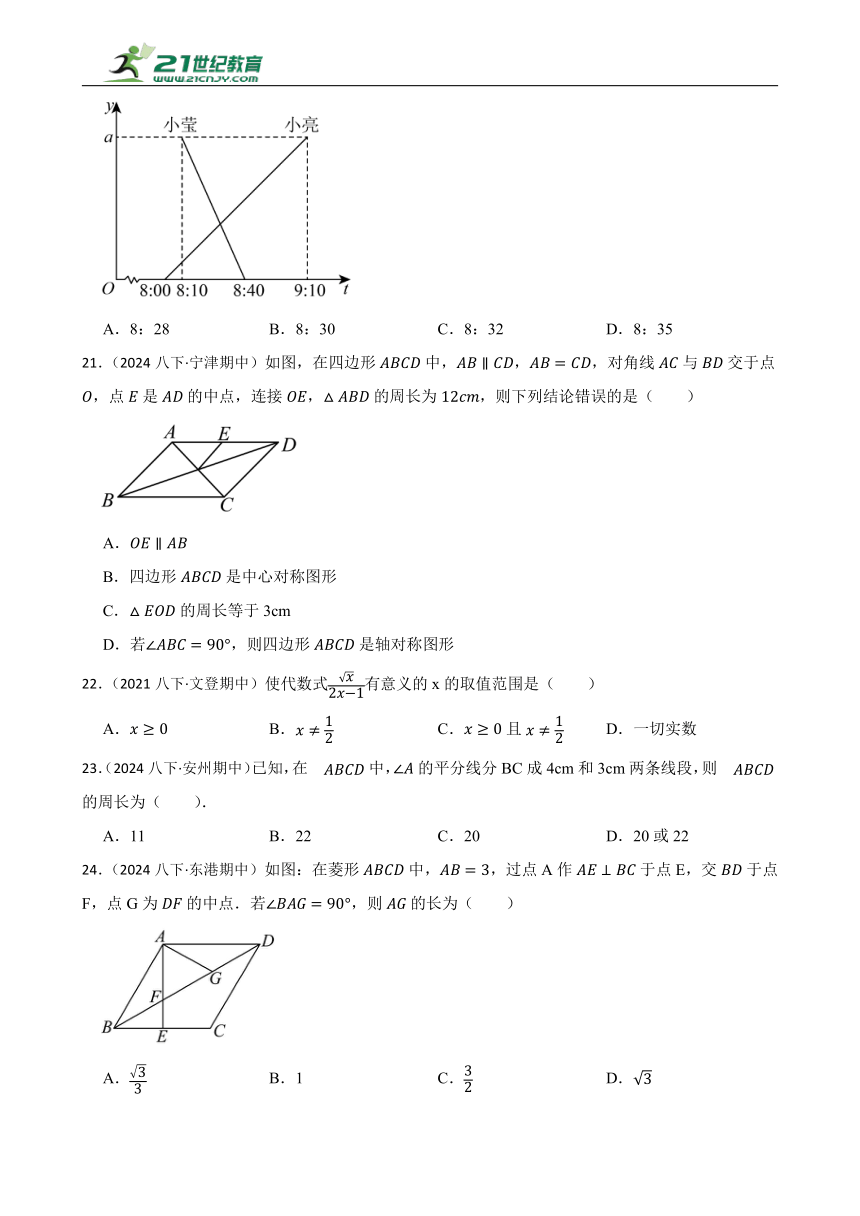
20.(2024八下·无棣期中)甲乙两地相距a千米,小亮8:00乘慢车从甲地去乙地,10分钟后小莹乘快车从乙地赶往甲地.两人分别距甲地的距离y(千米)与两人行驶时刻t(×时×分)的函数图象如图所示,则小亮与小莹相遇的时刻为( )
A.8:28 B.8:30 C.8:32 D.8:35
21.(2024八下·宁津期中)如图,在四边形中,,,对角线与交于点,点是的中点,连接,的周长为,则下列结论错误的是( )
A.
B.四边形是中心对称图形
C.的周长等于3cm
D.若,则四边形是轴对称图形
22.(2021八下·文登期中)使代数式有意义的x的取值范围是( )
A. B. C.且 D.一切实数
23.(2024八下·安州期中)已知,在中,的平分线分BC成4cm和3cm两条线段,则的周长为( ).
A.11 B.22 C.20 D.20或22
24.(2024八下·东港期中)如图:在菱形中,,过点A作于点E,交于点F,点G为的中点.若,则的长为( )
A. B.1 C. D.
25.(2024八下·无棣期中)如图,的对角线交于点,下列结论一定成立的是( )
A. B. C. D.
26.(2024八下·扶沟期中)如图,在平行四边形中,,,的平分线交于点,交的延长线于点则CF的长为( )
A.2 B.3 C.3.5 D.4
27.(2024八下·青岛期中)如图,在中,,将在平面内绕点A逆时针旋转到的位置,使,则旋转角的度数为( )
A. B. C. D.
28.(2024八下·南充期中)如图是边长为1的的正方形网格,已知的三个顶点均在正方形格点上,则边上的高是( )
A. B. C. D.
29.(2024八下·无棣期中)以下列各组数为边长,能组成直角三角形的是( )
A.8,15,17 B.4,5,6 C.5,8,10 D.8,39,40
30.(2024八下·东港期中)已知的三边之长分别为2、5、m,则等于( )
A. B. C.10 D.4
31.(2024八下·深圳期中)如图,四边形的对角线,相交于点O,,且,则添加下列一个条件能判定四边形是菱形的是( )
A. B. C. D.
32.(2024八下·丛台期中)已知四边形ABCD是平行四边形,对角线AC、BD交于点O,E是BC的中点,以下说法错误的是( )
A.OE= DC B.OA=OC C.∠BOE=∠OBA D.∠OBE=∠OCE
33.(2024八下·黄埔期中)如图,在正方形ABCD中,边长为2的等边三角形AEF的顶点E、F分别在BC和CD上.下列结论:①CE=CF;②∠AEB=75°;③BE+DF=EF;④S正方形ABCD=2+.其中正确的个数为( )
A.1 B.2 C.3 D.4
34.(2024八下·青岛期中)如图,直角三角形的三边,,,满足的关系.利用这个关系,探究下面的问题:如图,是腰长为1的等腰直角三角形,,延长至,使,以为底,在外侧作等腰直角三角形,再延长至,使,以为底,在外侧作等腰直角三角形,……,按此规律作等 直角三角形(,为正整数),则的长及的面积分别是( )
A., B., C., D.,
35.(2024八下·青岛期中)如图,将线段AB先绕原点O按逆时针方向旋转90°,再向下平移4个单位,得到线段CD,则点A的对应点C的坐标是( )
A.(1,﹣6) B.(﹣1,6)
C.(1,﹣2) D.(﹣1,﹣2)
36.(2024八下·无棣期中)如图,平行四边形的对角线相交于点O,的平分线与边相交于点P,是中点,若,则的长为( )
A.6 B.4 C.3 D.2
37.(2024八下·宁津期中)如图,的对角线、交于点O,平分交于点E,且,,连接.下列结论:①;②;③;④;成立的个数有( )
A.1个 B.2个 C.3个 D.4个
38.(2024八下·宁津期中)如图,在平行四边形中,平分,则平行四边形的周长是( )
A. B. C. D.
39.(2024八下·宁津期中)如图,在矩形中,,,将矩形沿折叠,点D落在点处,则的长为( )
A. B. C. D.
40.(2024八下·宁津期中)若顺次连接四边形各边中点所得的四边形是菱形,则四边形必定是( )
A.菱形 B.对角线相互垂直的四边形
C.正方形 D.对角线相等的四边形
41.(2024八下·宁津期中)下列命题的逆命题是真命题的是( )
A.对顶角相等
B.菱形的对角相等
C.对角线互相平分的四边形是平行四边形
D.全等三角形的对应角相等
42.(2024八下·宁津期中)如图,在中,E、F、G分别是三边的中点,若四边形是菱形,则应当满足的条件是( )
A.任意三角形 B. C. D.
43.(2024八下·宁津期中)下列式子是二次根式的是( )
A. B. C. D.
44.(2024八下·无棣期中)如图,△ABC的顶点A、B、C在边长为1的正方形网格的格点上,BD⊥AC于点D,则CD的长为( )
A. B. C. D.
45.(2024八下·无棣期中)下列命题正确的是( )
A.一组邻边相等的四边形是菱形
B.对角互补的四边形是平行四边形
C.矩形的对角线互相垂直
D.正方形的对角线相等且互相平分
46.(2024八下·东港期中)如图,在正方形中,点,分别是,的中点,,相交于点,为上一点,为的中点.若,,则线段的长度为( )
A. B. C.2 D.
47.(2024八下·市中区期中)已知关于x的分式方程的解为非正数,则m的取值范围是( )
A. B.
C.且 D.且
48.(2024八下·吐鲁番期中)下列说法中,错误的是( )
A.菱形的对角线互相垂直
B.矩形的四个内角都相等
C.对角线互相垂直的四边形是菱形
D.四个内角都相等的四边形是矩形
49.(2024八上·襄都期中)已知,则的平方根为( )
A. B. C. D.
50.(2024八下·阳信期中)对于直线的描述正确的是( )
A.y随x的增大而增大 B.与y轴的交点是
C.经过点 D.图象不经过第二象限
答案解析部分
1.B
解:A. 若,则,故该选项不成立,不符合题意;
B. 若,则,故该选项成立,符合题意;
C. 若,时,有,故该选项不一定成立,不符合题意;
D. 若,则,故该选项不成立,不符合题意;
故答案为:B.
根据不等式的性质逐项进行判断即可求出答案.
2.C
3.B
4.B
5.C
6.B
7.B
由菱形ABCD可得,AB∥CD,AC平分∠BAD,
∴∠BAD+∠ADC=180°,
∵∠ADC=180°-∠1-∠2=180°-25°-75°=80°,
∴∠BAD=100°,
∴∠BAC=∠BAD=50°。
故答案为:B
根据菱形 的性质可得出BAD+∠ADC=180°,求出∠ADC可得∠BAD,再根据AC平分∠BAD可得∠BAC。
8.C
9.C
10.A
解:由作图过程可知:
MN是AC的垂直平分线,交AC于点E,
∴DA=DC,
∴∠DAC=∠C=30°,
∴∠ADB=60°,
∵AB=BD=4,
∴△ABD是等边三角形,
∴AD=AB=BD=4,
在Rt△DCE中,DC=4,∠C=30°,
∴DE=2,CE=2,
∴AC=2CE=4,
∴S△ADC= AC DE=×4×2=4.
故答案为:A.
根据作图过程可得MN是AC的垂直平分线,交AC于点E,得DA=DC,根据∠C=30°,根据等边三角形判定定理可得AD=AB=BD=4,再根据含30°角的直角三角形性质可得DE=2,CE=2,则AC=2CE=4,再根据三角形面积即可求出答案.
11.B
12.D
13.C
14.D
解:根据正方形的判别方法知,两条对角线互相垂直平分的四边形是菱形,且相等又可判定为正方形,故选D.
两条对角线互相垂直平分的四边形是菱形,对角线相等的菱形是正方形,所以该四边形是正方形.
15.A
16.B
17.B
18.C
解:∵四边形ABCD是平行四边形,AC=12,
∴OA=AC=6,BD=2OB,
∵AB⊥AC,AB=8,
∴OB==10,
∴BD=2OB=20.
故选C.
由四边形ABCD是平行四边形,根据平行四边形的对角线互相平分,可得OA的长,然后由AB⊥AC,AB=8,AC=12,根据勾股定理可求得OB的长,继而求得答案.
19.A
20.A
21.C
22.C
解:根据二次根式被开方数必须是非负数和分式分母不为0的条件,要使在实数范围内有意义,必须.
故答案为:C.
根据分式及二次根式有意义的条件可得 ,再求出x的取值范围即可。
23.D
24.D
25.C
26.B
27.B
解:由旋转的性质得.
∵,,
∴.
∵,
∴,
∴.
故答案为:B.
由旋转的性质得由旋转的性质得,再根据直线平行性质可得,再根据等边对等角可得,再根据三角形内角和定理即可求出答案.
28.A
29.A
30.A
31.B
解:A、证明四边形是平行四边形, ,可得四边形是矩形,选项错误.
B、证明四边形是平行四边形,,可得对角线互相垂直平分,能证明是菱形,选项正确.
C、证明四边形是平行四边形,可得是矩形,选项错误.
D、证明四边形是平行四边形,,条件没用,选项错误.
故答案为:B.
根据菱形的判定定理逐项判断即可.
32.D
解:∵四边形ABCD是平行四边形,
∴OA=OC,OB=OD,AB∥DC,
又∵点E是BC的中点,
∴OE是△BCD的中位线,
∴OE= DC,OE∥DC,
∴OE∥AB,
∴∠BOE=∠OBA,
∴选项A、B、C正确;
∵OB≠OC,
∴∠OBE≠∠OCE,
∴选项D错误;
故选:D.
由平行四边形的性质和三角形中位线定理得出选项A、B、C正确;由OB≠OC,得出∠OBE≠∠OCE,选项D错误;即可得出结论.
33.C
解:∵四边形ABCD是正方形,
∴AB=AD,
∵△AEF是等边三角形,
∴AE=AF,
在Rt△ABE和Rt△ADF中,,
∴Rt△ABE≌Rt△ADF(HL),
∴BE=DF,
∵BC=DC,
∴BC–BE=CD–DF,
∴CE=CF,
∴①说法正确;
∵CE=CF,
∴△ECF是等腰直角三角形,
∴∠CEF=45°,
∵∠AEF=60°,
∴∠AEB=75°,
∴②说法正确;
如图,连接AC,交EF于G点,
∴AC⊥EF,且AC平分EF,
∵∠CAF≠∠DAF,
∴DF≠FG,
∴BE+DF≠EF,
∴③说法错误;
∵EF=2,
∴CE=CF=,设正方形的边长为a,
在Rt△ADF中,a2+(a–)2=4,
解得a=,
则a2=2+,
∴S正方形ABCD=2+,
④说法正确,
∴正确的有①②④.
故答案为:C.
根据正方形性质可得AB=AD,再根据等边三角形性质可得AE=AF,由全等三角形判定定理可得Rt△ABE≌Rt△ADF(HL),则BE=DF,再根据边之间的关系可判断①;根据等腰直角三角形判定定理可得△ECF是等腰直角三角形,则∠CEF=45°,再根据角之间的关系可判断②;连接AC,交EF于G点,根据垂直平分线性质可判断③;设正方形的边长为a,根据勾股定理建立方程,解方程可得a2=2+,再根据正方形面积可判断④.
34.B
解:是腰长为1的等腰直角三角形,
,
,
,
为等腰直角三角形,
.
同理,
,
.
同理,
,
.
依此类推:.
故答案为:B.
根据等腰直角三角形的性质分别求出、和的长度,从而找出规律,求出长度,即可求出的面积.
35.D
解:由题意可得如下图形:
∴由图象可知:点A的对应点C的坐标是(﹣1,﹣2);
故答案为:D.
根据旋转及平移的性质画出图形,结合图象即可求出答案.
36.D
37.A
38.C
39.B
40.D
41.C
42.C
43.B
44.A
45.D
46.A
47.C
48.C
解:A、菱形的对角线互相垂直,A不符合题意;
B、矩形的四个内角都相等为90°,B不符合题意;
C、对角线互相垂直平分的四边形是菱形,C符合题意;
D、四个内角都相等的四边形是矩形,D不符合题意;
故答案为:C.
利用菱形,矩形的判定与性质对每个选项一一判断即可。
49.D
50.B
期中真题专项复习01 选择题
一、选择题
1.(2024八下·青岛期中)若,则下列不等式一定成立的是( )
A. B. C. D.
2.(2024八下·潍坊期中)若的小数部分是a,则的值为( )
A.1 B. C.3 D.12
3.(2024八下·淄博期中)如图,在正方形中,F是边上的一点,连结并延长与的延长线相交于点E.若,则的值为( )
A. B. C. D.
4.(2024八下·聊城期中)若关于x的不等式组无解,则实数m的取值范围是( )
A. B. C. D.
5.(2024八下·聊城期中)下列实数中的无理数是( )
A. B.0 C. D.
6.(2022八下·港北期中)如图,在中,分别是的中点,点在延长线上,添加一个条件使四边形为平行四边形,则这个条件是( )
A. B. C. D.
7.(2024八下·徐闻期中)如图,四边形是菱形,过点的直线分别交,的延长线于点,,若,,则等于( )
A. B. C. D.
8.(2024八下·宁津期中)菱形ABCD中,AC=10,BD=24,则该菱形的面积等于( )
A.13 B.52 C.120 D.240
9.(2024八下·金川期中)如图,边长为的正方形两边与坐标轴正半轴重合,点的坐标是( )
A. B. C. D.
10.(2024八下·青岛期中)如图,在△ABC中,按以下步骤作图:①分别以点A和点C为圆心,以大于AC的长为半径作弧,两弧相交于M、N两点;②作直线MN交BC于点D,连接AD.若AB=BD,AB=4,∠C=30°,则△ACD的面积为( )
A. B. C. D.13
11.(2024八下·南山期中)如图,直角中,,,BC=4,点E是边上一点,将绕点B顺时针旋转到点F,则长的最小值是( )
A. B.2 C. D.
12.(2024八下·梁山期中)二次根式在实数范围内有意义,则的取值范围在数轴上表示正确的是( )
A.
B.
C.
D.
13.(2024八下·平阴期中)如图,在平面直角坐标系中,直线与轴、轴分别交于点A、B,且与直线相交于点.直接写出的解集( )
A. B. C. D.
14.(2024八下·汕头期中)两条对角线相等且互相垂直平分的四边形是( )
A.平行四边形 B.矩形
C.菱形 D.正方形
15.(2024八下·红古期中)如图,将绕点A逆时针旋转得到,若,则的度数为( )
A. B. C. D..
16.(2022八下·曲阳期中)函数的自变量的取值范围是( )
A.x>0且x≠ B.x≥0且x≠ C.x≥0 D.x≠
17.(2024八下·宁津期中)下列二次根式中,最简二次根式是( )
A. B. C. D.
18.(2024八下·杭州期中)如图,四边形ABCD是平行四边形,O是对角线AC与BD的交点,AB⊥AC,若AB=8,AC=12,则BD的长是( )
A.16 B.18 C.20 D.22
19.(2024八下·邳州期中)如图,正方形ABCD和正方形CEFG中,点D在CG上,已知BC=1,CE=7,点H是AF的中点,则CH的长是( )
A.5 B.3.5 C.4 D.
20.(2024八下·无棣期中)甲乙两地相距a千米,小亮8:00乘慢车从甲地去乙地,10分钟后小莹乘快车从乙地赶往甲地.两人分别距甲地的距离y(千米)与两人行驶时刻t(×时×分)的函数图象如图所示,则小亮与小莹相遇的时刻为( )
A.8:28 B.8:30 C.8:32 D.8:35
21.(2024八下·宁津期中)如图,在四边形中,,,对角线与交于点,点是的中点,连接,的周长为,则下列结论错误的是( )
A.
B.四边形是中心对称图形
C.的周长等于3cm
D.若,则四边形是轴对称图形
22.(2021八下·文登期中)使代数式有意义的x的取值范围是( )
A. B. C.且 D.一切实数
23.(2024八下·安州期中)已知,在中,的平分线分BC成4cm和3cm两条线段,则的周长为( ).
A.11 B.22 C.20 D.20或22
24.(2024八下·东港期中)如图:在菱形中,,过点A作于点E,交于点F,点G为的中点.若,则的长为( )
A. B.1 C. D.
25.(2024八下·无棣期中)如图,的对角线交于点,下列结论一定成立的是( )
A. B. C. D.
26.(2024八下·扶沟期中)如图,在平行四边形中,,,的平分线交于点,交的延长线于点则CF的长为( )
A.2 B.3 C.3.5 D.4
27.(2024八下·青岛期中)如图,在中,,将在平面内绕点A逆时针旋转到的位置,使,则旋转角的度数为( )
A. B. C. D.
28.(2024八下·南充期中)如图是边长为1的的正方形网格,已知的三个顶点均在正方形格点上,则边上的高是( )
A. B. C. D.
29.(2024八下·无棣期中)以下列各组数为边长,能组成直角三角形的是( )
A.8,15,17 B.4,5,6 C.5,8,10 D.8,39,40
30.(2024八下·东港期中)已知的三边之长分别为2、5、m,则等于( )
A. B. C.10 D.4
31.(2024八下·深圳期中)如图,四边形的对角线,相交于点O,,且,则添加下列一个条件能判定四边形是菱形的是( )
A. B. C. D.
32.(2024八下·丛台期中)已知四边形ABCD是平行四边形,对角线AC、BD交于点O,E是BC的中点,以下说法错误的是( )
A.OE= DC B.OA=OC C.∠BOE=∠OBA D.∠OBE=∠OCE
33.(2024八下·黄埔期中)如图,在正方形ABCD中,边长为2的等边三角形AEF的顶点E、F分别在BC和CD上.下列结论:①CE=CF;②∠AEB=75°;③BE+DF=EF;④S正方形ABCD=2+.其中正确的个数为( )
A.1 B.2 C.3 D.4
34.(2024八下·青岛期中)如图,直角三角形的三边,,,满足的关系.利用这个关系,探究下面的问题:如图,是腰长为1的等腰直角三角形,,延长至,使,以为底,在外侧作等腰直角三角形,再延长至,使,以为底,在外侧作等腰直角三角形,……,按此规律作等 直角三角形(,为正整数),则的长及的面积分别是( )
A., B., C., D.,
35.(2024八下·青岛期中)如图,将线段AB先绕原点O按逆时针方向旋转90°,再向下平移4个单位,得到线段CD,则点A的对应点C的坐标是( )
A.(1,﹣6) B.(﹣1,6)
C.(1,﹣2) D.(﹣1,﹣2)
36.(2024八下·无棣期中)如图,平行四边形的对角线相交于点O,的平分线与边相交于点P,是中点,若,则的长为( )
A.6 B.4 C.3 D.2
37.(2024八下·宁津期中)如图,的对角线、交于点O,平分交于点E,且,,连接.下列结论:①;②;③;④;成立的个数有( )
A.1个 B.2个 C.3个 D.4个
38.(2024八下·宁津期中)如图,在平行四边形中,平分,则平行四边形的周长是( )
A. B. C. D.
39.(2024八下·宁津期中)如图,在矩形中,,,将矩形沿折叠,点D落在点处,则的长为( )
A. B. C. D.
40.(2024八下·宁津期中)若顺次连接四边形各边中点所得的四边形是菱形,则四边形必定是( )
A.菱形 B.对角线相互垂直的四边形
C.正方形 D.对角线相等的四边形
41.(2024八下·宁津期中)下列命题的逆命题是真命题的是( )
A.对顶角相等
B.菱形的对角相等
C.对角线互相平分的四边形是平行四边形
D.全等三角形的对应角相等
42.(2024八下·宁津期中)如图,在中,E、F、G分别是三边的中点,若四边形是菱形,则应当满足的条件是( )
A.任意三角形 B. C. D.
43.(2024八下·宁津期中)下列式子是二次根式的是( )
A. B. C. D.
44.(2024八下·无棣期中)如图,△ABC的顶点A、B、C在边长为1的正方形网格的格点上,BD⊥AC于点D,则CD的长为( )
A. B. C. D.
45.(2024八下·无棣期中)下列命题正确的是( )
A.一组邻边相等的四边形是菱形
B.对角互补的四边形是平行四边形
C.矩形的对角线互相垂直
D.正方形的对角线相等且互相平分
46.(2024八下·东港期中)如图,在正方形中,点,分别是,的中点,,相交于点,为上一点,为的中点.若,,则线段的长度为( )
A. B. C.2 D.
47.(2024八下·市中区期中)已知关于x的分式方程的解为非正数,则m的取值范围是( )
A. B.
C.且 D.且
48.(2024八下·吐鲁番期中)下列说法中,错误的是( )
A.菱形的对角线互相垂直
B.矩形的四个内角都相等
C.对角线互相垂直的四边形是菱形
D.四个内角都相等的四边形是矩形
49.(2024八上·襄都期中)已知,则的平方根为( )
A. B. C. D.
50.(2024八下·阳信期中)对于直线的描述正确的是( )
A.y随x的增大而增大 B.与y轴的交点是
C.经过点 D.图象不经过第二象限
答案解析部分
1.B
解:A. 若,则,故该选项不成立,不符合题意;
B. 若,则,故该选项成立,符合题意;
C. 若,时,有,故该选项不一定成立,不符合题意;
D. 若,则,故该选项不成立,不符合题意;
故答案为:B.
根据不等式的性质逐项进行判断即可求出答案.
2.C
3.B
4.B
5.C
6.B
7.B
由菱形ABCD可得,AB∥CD,AC平分∠BAD,
∴∠BAD+∠ADC=180°,
∵∠ADC=180°-∠1-∠2=180°-25°-75°=80°,
∴∠BAD=100°,
∴∠BAC=∠BAD=50°。
故答案为:B
根据菱形 的性质可得出BAD+∠ADC=180°,求出∠ADC可得∠BAD,再根据AC平分∠BAD可得∠BAC。
8.C
9.C
10.A
解:由作图过程可知:
MN是AC的垂直平分线,交AC于点E,
∴DA=DC,
∴∠DAC=∠C=30°,
∴∠ADB=60°,
∵AB=BD=4,
∴△ABD是等边三角形,
∴AD=AB=BD=4,
在Rt△DCE中,DC=4,∠C=30°,
∴DE=2,CE=2,
∴AC=2CE=4,
∴S△ADC= AC DE=×4×2=4.
故答案为:A.
根据作图过程可得MN是AC的垂直平分线,交AC于点E,得DA=DC,根据∠C=30°,根据等边三角形判定定理可得AD=AB=BD=4,再根据含30°角的直角三角形性质可得DE=2,CE=2,则AC=2CE=4,再根据三角形面积即可求出答案.
11.B
12.D
13.C
14.D
解:根据正方形的判别方法知,两条对角线互相垂直平分的四边形是菱形,且相等又可判定为正方形,故选D.
两条对角线互相垂直平分的四边形是菱形,对角线相等的菱形是正方形,所以该四边形是正方形.
15.A
16.B
17.B
18.C
解:∵四边形ABCD是平行四边形,AC=12,
∴OA=AC=6,BD=2OB,
∵AB⊥AC,AB=8,
∴OB==10,
∴BD=2OB=20.
故选C.
由四边形ABCD是平行四边形,根据平行四边形的对角线互相平分,可得OA的长,然后由AB⊥AC,AB=8,AC=12,根据勾股定理可求得OB的长,继而求得答案.
19.A
20.A
21.C
22.C
解:根据二次根式被开方数必须是非负数和分式分母不为0的条件,要使在实数范围内有意义,必须.
故答案为:C.
根据分式及二次根式有意义的条件可得 ,再求出x的取值范围即可。
23.D
24.D
25.C
26.B
27.B
解:由旋转的性质得.
∵,,
∴.
∵,
∴,
∴.
故答案为:B.
由旋转的性质得由旋转的性质得,再根据直线平行性质可得,再根据等边对等角可得,再根据三角形内角和定理即可求出答案.
28.A
29.A
30.A
31.B
解:A、证明四边形是平行四边形, ,可得四边形是矩形,选项错误.
B、证明四边形是平行四边形,,可得对角线互相垂直平分,能证明是菱形,选项正确.
C、证明四边形是平行四边形,可得是矩形,选项错误.
D、证明四边形是平行四边形,,条件没用,选项错误.
故答案为:B.
根据菱形的判定定理逐项判断即可.
32.D
解:∵四边形ABCD是平行四边形,
∴OA=OC,OB=OD,AB∥DC,
又∵点E是BC的中点,
∴OE是△BCD的中位线,
∴OE= DC,OE∥DC,
∴OE∥AB,
∴∠BOE=∠OBA,
∴选项A、B、C正确;
∵OB≠OC,
∴∠OBE≠∠OCE,
∴选项D错误;
故选:D.
由平行四边形的性质和三角形中位线定理得出选项A、B、C正确;由OB≠OC,得出∠OBE≠∠OCE,选项D错误;即可得出结论.
33.C
解:∵四边形ABCD是正方形,
∴AB=AD,
∵△AEF是等边三角形,
∴AE=AF,
在Rt△ABE和Rt△ADF中,,
∴Rt△ABE≌Rt△ADF(HL),
∴BE=DF,
∵BC=DC,
∴BC–BE=CD–DF,
∴CE=CF,
∴①说法正确;
∵CE=CF,
∴△ECF是等腰直角三角形,
∴∠CEF=45°,
∵∠AEF=60°,
∴∠AEB=75°,
∴②说法正确;
如图,连接AC,交EF于G点,
∴AC⊥EF,且AC平分EF,
∵∠CAF≠∠DAF,
∴DF≠FG,
∴BE+DF≠EF,
∴③说法错误;
∵EF=2,
∴CE=CF=,设正方形的边长为a,
在Rt△ADF中,a2+(a–)2=4,
解得a=,
则a2=2+,
∴S正方形ABCD=2+,
④说法正确,
∴正确的有①②④.
故答案为:C.
根据正方形性质可得AB=AD,再根据等边三角形性质可得AE=AF,由全等三角形判定定理可得Rt△ABE≌Rt△ADF(HL),则BE=DF,再根据边之间的关系可判断①;根据等腰直角三角形判定定理可得△ECF是等腰直角三角形,则∠CEF=45°,再根据角之间的关系可判断②;连接AC,交EF于G点,根据垂直平分线性质可判断③;设正方形的边长为a,根据勾股定理建立方程,解方程可得a2=2+,再根据正方形面积可判断④.
34.B
解:是腰长为1的等腰直角三角形,
,
,
,
为等腰直角三角形,
.
同理,
,
.
同理,
,
.
依此类推:.
故答案为:B.
根据等腰直角三角形的性质分别求出、和的长度,从而找出规律,求出长度,即可求出的面积.
35.D
解:由题意可得如下图形:
∴由图象可知:点A的对应点C的坐标是(﹣1,﹣2);
故答案为:D.
根据旋转及平移的性质画出图形,结合图象即可求出答案.
36.D
37.A
38.C
39.B
40.D
41.C
42.C
43.B
44.A
45.D
46.A
47.C
48.C
解:A、菱形的对角线互相垂直,A不符合题意;
B、矩形的四个内角都相等为90°,B不符合题意;
C、对角线互相垂直平分的四边形是菱形,C符合题意;
D、四个内角都相等的四边形是矩形,D不符合题意;
故答案为:C.
利用菱形,矩形的判定与性质对每个选项一一判断即可。
49.D
50.B
同课章节目录
