期中真题专项复习04 解答题(含答案)--2024-2025学年七年级数学下册(青岛版2024)
文档属性
| 名称 | 期中真题专项复习04 解答题(含答案)--2024-2025学年七年级数学下册(青岛版2024) |

|
|
| 格式 | docx | ||
| 文件大小 | 480.0KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-03-30 00:00:00 | ||
图片预览




文档简介
2024-2025学年七年级数学下册(青岛版2024)
期中真题专项复习04 解答题
一、解答题
1.(2024七下·青岛期中)如图,在一块正方形的钢板中挖去两个边长分别为a,b的小正方形.
(1)求剩余钢板的面积;
(2)若原钢板的周长是40,且,求剩余钢板的面积.
2.(2024七下·济南期中)如图,在中,为边上的高,点为边上的一点,连接.
(1)当为边上的中线时,若,的面积为24,求的长;
(2)当为的平分线时,若,,求的度数.
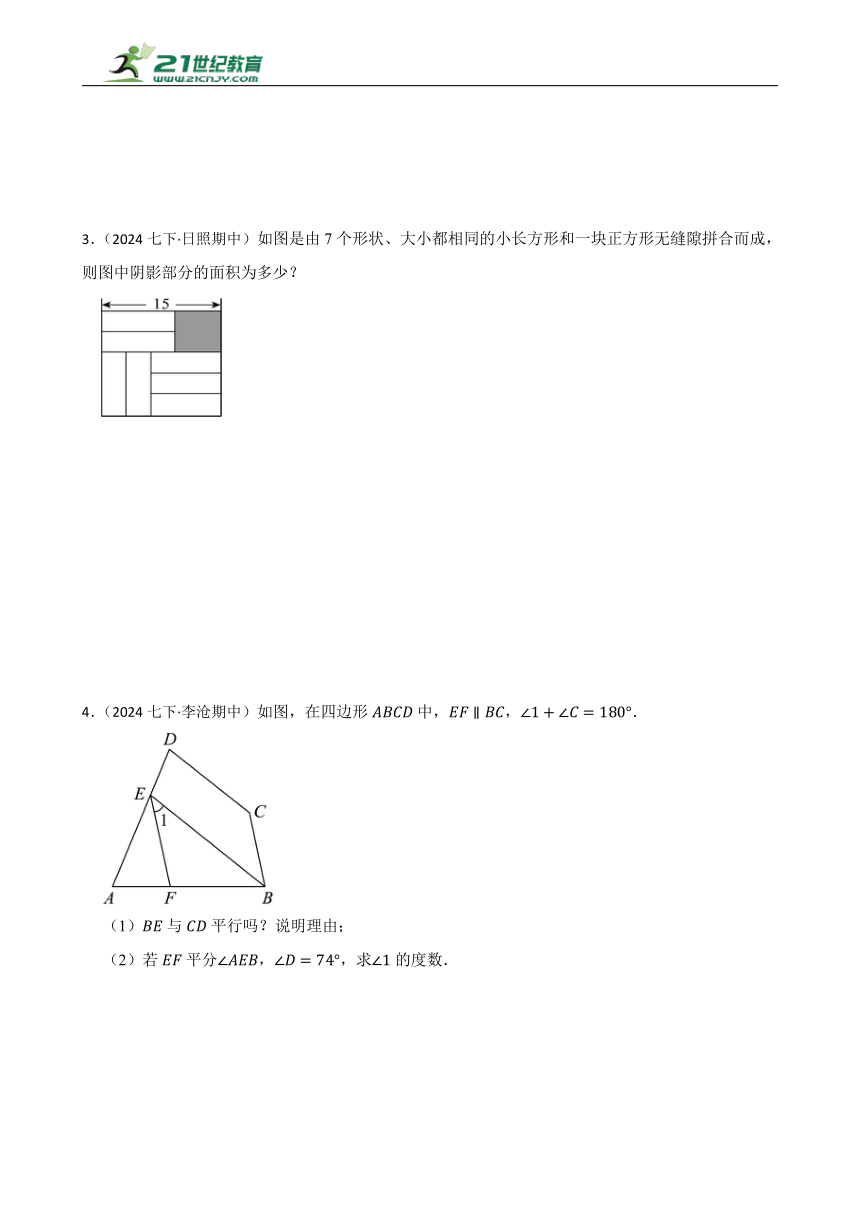
3.(2024七下·日照期中)如图是由7个形状、大小都相同的小长方形和一块正方形无缝隙拼合而成,则图中阴影部分的面积为多少?
4.(2024七下·李沧期中)如图,在四边形中,,.
(1)与平行吗?说明理由;
(2)若平分,,求的度数.
5.(2024七下·青岛期中)对于一个图形,通过两种不同的方法计算它的面积,可以得到一个数学等式,例如图1可以得到,请解答下列问题:
(1)图2所表示的数学等式为___________;
(2)利用(1)得到的结论,解决问题:若,求的值;
(3)如图3,将两个边长分别为a和b的正方形拼在一起,三点在同一直线上,连接,若两正方形的边长满足,求阴影部分面积.
6.(2024七下·东港期中)在解方程组时,由于甲看错了方程(1)中的m值,使得方程的解为,乙看错了方程(2)中的n值,得到的方程组的解为,求代数式的平方根,并求出原方程组的解
7.(2024七下·乳山期中)如图,在中,平分,交于点D,于点E,,,求的度数.
8.(2024七下·市南区期中) 如图,已知∠1=∠BDC,∠2+∠3=180°.
(1)问AD与CE平行吗?如果平行请说明理由.
(2)若CE⊥AE于E,DA平分∠BDC,∠FAB=68°,求∠1的度数.
9.(2024七下·济南期中) 学习整式的乘法时可以发现:用两种不同的方法表示同一个图形的面积,可以得到一个等式,进而可以利用得到的等式解决问题.
(1)如图,是由边长为,的正方形和长为、宽为的长方形拼成的大正方形,由图可得等式: ;
(2)知识迁移:
如图是用个小正方体和个小长方体拼成的一个大正方体,类比,用不同的方法表示这个大正方体的体积,则可得等式: ;
已知,,,利用中所得等式,求代数式的值.
10.(2024七下·冠县期中)某商场投入13800元资金购进甲、乙两种矿泉水共500箱,矿泉水的成本价和销售价如表所示:
类别/单价 成本价 销售价(元/箱)
甲 24 36
乙 33 48
(1)该商场购进甲、乙两种矿泉水各多少箱?
(2)全部售完500箱矿泉水,该商场共获得利润多少元?
11.(2024七下·牟平期中)“文明其精神,野蛮其体魄”,为进一步提升学生的健康水平,我市某校计划用760元购买14个体育用品,备选体育用品及单价如表:
备选体育用品 足球 篮球 排球
单价(元) 80 60 40
(1)若760元全部用来购买足球和排球,求足球和排球各购买的数量.
(2)若该校先用一部分资金购买了a个排球,再用剩下的资金购买了足球和篮球,且篮球和足球的个数相同,此时正好剩余80元,求a的值.
(3)由于篮球和排球都不够分配,该校再补充采购这两种球共花费了480元,其中这两种球都至少购进2个,则有几种补购方案?
12.(2024七下·济南期中) 中,,,过点作连接,,为平面内一动点.
(1)如图,若,则 .
(2)如图,点在上,且于,过点作于,为中点,连接并延长,交于点.
求证:≌;;
(3)如图,连接,,过点作于点,且满足,连接,,过点作于点,若,,,求线段的长度的取值范围.
13.(2024七下·瓜州期中)先阅读下面的内容,再解决问题,
例题:若 6n+9=0,求m和n的值.
∵ 6n+9=0
∴ 6n+9=0
∴
∴m+n=0,n 3=0
∴m= 3,n=3
问题:若 2xy+4y+4=0,求的值.
14.(2024七下·章丘期中)(1)如图1,已知,,可得 度;
(2)如图2,在(1)的条件下,如果平分,求度数;
(3)如图3,在(1)(2)的条件下,如果,则 度;
(4)尝试解决下面问题:如图4,,,是的平分线,,求的度数.
15.(2017七下·濮阳期中)如图,EF∥AD,AD∥BC,CE平分∠BCF,∠DAC=120°,∠ACF=20°,求∠FEC的度数.
16.(2024七下·荣成期中)如图,在中,边的垂直平分线交于点D,边的垂直半分线交于点E,与相交于点O,连接,若的周长为,的周长为.
(1)求线段的长;
(2)连接,求线段的长;
(3)若,求的度数.
17.(2024七下·市中区期中)(1)先化简,再求值:,其中,.
(2)已知,求代数式的值.
18.(2024七下·青岛期中)【知识回顾】我们在学习代数式求值时,遇到这样一类题:代数式的值与x的取值无关,求a的值.
通常的解题思路是:把x、y看作字母,a看作系数,合并同类项.因为代数式的值与x的取值无关,所以含x项的系数为0.
具体解题过程是:原式,
代数式的值与x的取值无关,
,解得.
【理解应用】(1)若关于x的多项式的值与x的取值无关,求m值;
(2)已知,,且的值与x的取值无关,求m的值;
【能力提升】(3)7张如图1的小长方形,长为a,宽为b,按照图2方式不重叠地放在大长方形内,大长方形中未被覆盖的两个部分都是长方形. 设右上角的面积为,左下角的面积为,当的长变化时,的值始终保持不变,求a与b的等量关系.
19.(2024七下·台儿庄期中)在图1中,三种不同大小的正方形与长方形,拼成了一个如图2所示的正方形.
(1)根据图 2 中的阴影部分面积关系直接写出下列代数式之间的数量关系:___________;
(2)已知,求和的值;
(3)已知,求的值.
20.(2024七下·莱芜期中)为了适合不同人群的口味,莱芜信誉楼超市购进了巧克力味、牛奶味的两种草莓进行销售.已知箱巧克力味的进价与箱牛奶味的进价的和为元,且每箱巧克力味的进价比每箱牛奶味的进价贵元.
(1)求每箱巧克力味的进价与每箱牛奶味的进价分别是多少元?
(2)如果某一天超市购进了巧克力味的草莓箱,且每箱价格提高出售,购进了牛奶味的草莓箱,且每箱价格提高出售,问这一天超市全部卖完利润为多少元?
21.(2024七下·乳山期中)如图,点在的边上,交于点,连接,,,,.求的度数.
22.(2024七下·桐柏期中)已知关于 x、y 的二元一次方程组.
(1)当时,解这个方程组;
(2)若,设,求S的取值范围.
23.(2024七下·兖州期中)如图,在长方形中,,,,,将长方形沿着直线折叠,使点C落在处,交于点E,求的度数.
24.(2024七下·宁津期中)(1)已知关于x,y的二元一次方程组的解互为相反数,求k的值.
(2)甲、乙两位同学在解方程组时,甲看错了第一个方程,解得 ,乙看错了第二个方程,解得 ,求+b3的值.
25.(2024七下·昌乐期中)如图,某小区有一块长为米,宽为米的长方形地块,物业公司计划在小区内修一条平行四边形小路,小路的底边宽为米,将阴影部分进行绿化.
(1)用含有、的式子表示绿化的总面积;
(2)若,,求出此时绿化的总面积.
26.(2024七下·济南期中) 如图,在中,,分别是的中线和高,是的角平分线.
(1)若的面积为,,求的长;
(2)若,,求的大小.
27.(2024七下·泰山期中)如图,直线交的边、于,交延长线于,若,,,求的度数.
28.(2024七下·潍城期中)我们知道,一般的数学公式,法则、定义可以正向运用,也可以逆向运用.例如,“同底数幂的乘法”“幂的乘方”“积的乘方”这几个法则的逆向运用表现为:;
;;其中m,n为正整数.结合以上材料解决下列问题.
(1)已知,请把a,b,c用“”连接起来;
(2)若,求的值;
(3)化简:.
29.(2024七下·莱芜期中)将的顶角A沿直线DE折叠(如图),点A的对应点为点,记为,为.
(1)如图1,当点A的对应点落在内部时,试探求与的数量关系,并说明理由;
(2)如图2,当点A的对应点落在外部时,与又有怎样的数量关系呢?请写出猜想,并给予证明.
30.(2024七下·湖北期中)如图,在△ABC中,∠1=∠2,点E、F、G分别在BC、AB、AC上,且EF⊥AB,DG∥BC,请判断CD与AB的位置关系,并说明理由.
答案解析部分
1.(1)解:由题意得,剩余钢板的面积为:
=a2+2ab+b2-a2-b2
=2ab
(2)解:∵原钢板的周长是40,
∴,
∴,
∴
∵,
∴
∴,
∴,
∴剩余钢板的面积.
(1)由图可知大图形的边长为(a+b),阴影部分面积=大图形面积(a+b)2减去两个小图形面积a2+b2得结果为2ab;
(2)由周长4(a+b)为40得到,再由,可得,再代入(1)中2ab的代数式进行计算即可.
(1)解:由题意得,剩余钢板的面积为:
.
(2)解:∵原钢板的周长是40,
∴,
∴,
∴
∵,
∴
∴,
∴,
∴剩余钢板的面积.
2.(1);
(2).
3.解:设小长方形的长为x,宽为y,
由题意得,,
解得,
∴阴影部分的正方形边长为,
∴阴影部分的面积为:.
本题主要考查了二元一次方程组的应用,设小长方形的长为x,宽为y,结合长加上宽的两倍等于15,长为宽的三倍,列出方程组,求得方程组的解,即可得到答案.
4.(1)解:,理由如下:
,
,
,
,
;
(2)解:由(1)知,
,
,
平分,
.
(1)由,得到,进而求得,结合同旁内角互补,两直线平行,即可证得;
(2)由(1)知,得到,求得,再由平分,结合,即可求解.
5.(1);
(2)
(3)
6.的平方根为;原方程组的解为:
7.
8.(1)解:AD∥CE,
理由:∵∠1=∠BDC,
∴AB∥CD,
∴∠2=∠ADC,
∵∠2+∠3=180°,
∴∠3+∠ADC=180°,
∴AD∥CE;
(2)解:∵CE⊥AE,
∴∠CEA=90°,
∵CE∥AD,
∴∠CEA=∠DAF=90°,
∵∠FAB=68°,
∴∠2=∠DAF﹣∠FAB=22°,
∴∠2=∠ADC=22°,
∵DA平分∠CDF,
∴∠CDF=2∠ADC=44°,
∴∠1=∠CDF=44°,
∴∠1的度数为44°.
(1)利用已知可得AB∥CD,从而可得∠2=∠ADC,进而可得∠3+∠ADC=180°,然后利用同旁内角互补,两直线平行可得AD∥CE,即可解答;
(2)根据垂直定义可得∠CEA=90°,再利用(1)的结论可得∠CEA=∠DAF=90°,从而可得∠2=22°,然后利用(1)的结论可得∠2=∠ADC=22°,再利用角平分线的定义可得∠CDF=2∠ADC=44°,即可解答。熟练掌握平行线的判定与性质是解题的关键。
9.(1)
(2)解:;由拼图可知,大立方体的边长为,因此这个大正方体的体积为;这个大立方体是由个部分拼成的,这个部分的体积和为,因此有,故答案为:由得,,答:代数式的值为.
解:(1)由图(1)可知,大正方形的边长为a+b,因此这个正方形的面积为(a+b)2;
而这个大正方形由四个部分拼成的,这四个部分的面积和为a2+2ab+b2,
因此有(a+b)2=a2+2ab+b2,
故答案为:(a+b)2=a2+2ab+b2;
(2)①由拼图可知,大立方体的边长为a+b,因此这个大正方体的体积为(a+b)3;
这个大立方体是由6个部分拼成的,这6个部分的体积和为a3+3a2b+3ab2+b3,
因此有(a+b)3=a3+3a2b+3ab2+b3,
故答案为:(a+b)3=a3+3a2b+3ab2+b3;
(1)从整体和部分两个方面分别用代数式表示它们的面积即可;
(2)①从整体和部分两个方面用代数式表示大正方体体积即可得出答案;②利用①中的结论代入计算即可。
10.(1)商场购进甲种矿泉水300箱,购进乙种矿泉水200箱;(2)该商场共获得利润6600元.
11.(1)足球购买5个、排球购买9个;(2)a的值为10;(3)则有3种补购方案,分别为篮球购2个,排球购9个,或篮球购4个,排球购6个,或篮球购6个,排球购3个.
12.(1)8
(2)解:,
,,
,
在和中,
,
≌,
,,
,,
,
,
为中点,
,
又,
在和中,
,
≌,
,,
,
;
(3)解:连接,如图,
,
,
,
在和中,
,
≌,
,
,
,
,
,
在中,,
,
.
当点,点,点共线时,最大值为,最小值为,
.
解:(1)∵∠ABC=90°,AB=BC,BC=4,
∴S△ABC=×AB BC=8.
∵AE⊥AB,BC⊥AB,
∴AE∥BC,
∴S△EBC=S△ABC=8,
故答案为:8;
(1)由平行线的性质可得S△AEC=S△ABE,即可求解;
(2)由“AAS”可证△ABF≌△BCM,利用全等三角形的性质可得AF=BM,BF=CM,由“ASA”可证△ADF≌△CDH,利用相似三角形的性质可得AF=HC,DF=DH,可得结论;
(3)由“SAS”可证△CBM≌△ABM',可得CM=AM',由三角形的三边关系定理可求解。
13.
14.(1);(2);(3)67.5;(4)
15.解:∵EF∥AD,AD∥BC,
∴EF∥BC,
∴∠ACB+∠DAC=180°,
∵∠DAC=120°,
∴∠ACB=60°,
又∵∠ACF=20°,
∴∠FCB=∠ACB﹣∠ACF=40°,
∵CE平分∠BCF,
∴∠BCE=20°,
∵EF∥BC,
∴∠FEC=∠ECB,
∴∠FEC=20°.
推出EF∥BC,根据平行线性质求出∠ACB,求出∠FCB,根据角平分线求出∠ECB,根据平行线的性质推出∠FEC=∠ECB,代入即可.
16.(1)解:∵边的垂直平分线交于点D,边的垂直半分线交于点E,∴,
∴,
∵的周长为,即,
∴;
(2)解:连接,
∵边的垂直平分线交于点D,边的垂直半分线交于点E,
∴,
∵的周长为,即,,
∴;
(3)解:∵,∴,
∵,
∴,
∴,
∴.
(1)由边的垂直平分线交于点D,边的垂直半分线交于点E,根据线段垂直平分线的性质,得到,再由的周长为,列出算式,即可求得BC的长,得到答案;
(2)根据线段垂直平分线的性质,得到,结合的周长为,列出算式,即可求得OA的长,得到答案;
继而求解即可;
(3)根据三角形内角和定理,得出,再由,得到,结合,即可求解.
17.解:(1)
,
当,时,
原式;
(2)
,
∵,
∴,
∴原式
.
(1)根据整式的混合运算法则,结合完全平方公式、多项式与多项式的乘法、整式的除法的运算,化简得到,再将,,代入代数式,计算求值,即可得到答案;
(2)根据整式的混合运算法则,结合平方差公式、单项式与多项式的乘法的运算,化简得到,再由 ,整体代入求值,即可得到答案.
18.(1);(2);(3)
19.(1)
(2),
(3)16
20.(1)解:设每箱巧克力味的进价为元,每箱牛奶味的进价为元
由题意可得,,
解得:,
答:每箱巧克力味的进价为元,每箱牛奶味的进价为元:
(2)解:依题意,(元);
答:这一天超市全部卖完利润为元.
(1)设每箱巧克力味的进价为元,每箱牛奶味的进价为元,根据题意,列出二元一次方程组,求得方程组的解,即可得到答案;
(2)根据(1)的结论,结合超市购进了巧克力味的草莓箱,且每箱价格提高出售,购进了牛奶味的草莓箱,且每箱价格提高出售,列出算式,进行计算,即可得到答案.
(1)解:设每箱巧克力味的进价为元,每箱牛奶味的进价为元
由题意可得,,
解得:,
答:每箱巧克力味的进价为元,每箱牛奶味的进价为元:
(2)解:依题意,(元);
答:这一天超市全部卖完利润为元.
21.
22.(1)
(2)
23.解:由折叠可知,,,∵,
∴,
∵,
∴,
∴.
本题主要考查了平行线的性质,以及折叠的性质,根据折叠的性质,得到,,由,得到,再由,结合,即可求解.
24.(1)解:
①×3﹣②得:8(x+y)=3k-12,即x+y,
由题意得:x+y=0,即,
解得k=4.
(2)根据题意,得:,
解得:,
则b3(﹣1)31.
(1)方程组两方程相减表示出x+y,根据x与y互为相反数得到x+y=0,求出k的值即可;
(2)将x=1、y=﹣1代入第二个方程、将x=﹣2、y=﹣6代入第一个方程,列出关于a、b的方程组,求出a、b的值,再代入求解可得.
25.(1)平方米
(2)196平方米
26.(1)解:是的中线,,
,
是的高,的面积为,
,
;
(2)解:在中,为它的一个外角,且,,
,
是的角平分线,
,
.
(1)利用面积法求解即可.
(2)求出∠ABC,再根据∠BAF=90°-∠ABC即可求解。
27.
28.(1)解:∵
∴
(2)解:,∵,
∴原式;
(3)解:
.
(1)根据题意,利用逆用幂的乘方公式,将幂变为指数相同的幂,然后比较大小,即可得到答案;
(2)根据题意,利用逆用同底数幂和幂的乘方运算法则,化简得到进,将, 代入代数式,进行计算,即可求解;
(3)根据题意,利用逆用积的乘方运算法则,先计算乘方,结合乘法的结合律,进行计算,即可求解.
(1)解:∵
∴
(2)解:,
∵,
∴原式;
(3)解:
.
29.(1)解:,理由见解析:
如图1,连接,
是的外角,
.
同理,.
.
由折叠性质得.
.
(2)解:,证明如下:
如图2,连接,
是的外角,
.
同理,.
.
由折叠性质得.
,
.
30.解:CD⊥AB.理由如下:
∴DG∥BC,
∴∠1=∠DCB,
∵∠1=∠2,
∴∠2=∠DCB,
∴CD∥EF,
∴∠CDB=∠EFB,
∵EF⊥AB,
∴∠EFB=90°,
∴∠CDB=90°,
∴CD⊥AB.
由平行线的性质和已知条件可证明CD∥EF,可求得∠CDB=90°,可判断CD⊥AB.
期中真题专项复习04 解答题
一、解答题
1.(2024七下·青岛期中)如图,在一块正方形的钢板中挖去两个边长分别为a,b的小正方形.
(1)求剩余钢板的面积;
(2)若原钢板的周长是40,且,求剩余钢板的面积.
2.(2024七下·济南期中)如图,在中,为边上的高,点为边上的一点,连接.
(1)当为边上的中线时,若,的面积为24,求的长;
(2)当为的平分线时,若,,求的度数.
3.(2024七下·日照期中)如图是由7个形状、大小都相同的小长方形和一块正方形无缝隙拼合而成,则图中阴影部分的面积为多少?
4.(2024七下·李沧期中)如图,在四边形中,,.
(1)与平行吗?说明理由;
(2)若平分,,求的度数.
5.(2024七下·青岛期中)对于一个图形,通过两种不同的方法计算它的面积,可以得到一个数学等式,例如图1可以得到,请解答下列问题:
(1)图2所表示的数学等式为___________;
(2)利用(1)得到的结论,解决问题:若,求的值;
(3)如图3,将两个边长分别为a和b的正方形拼在一起,三点在同一直线上,连接,若两正方形的边长满足,求阴影部分面积.
6.(2024七下·东港期中)在解方程组时,由于甲看错了方程(1)中的m值,使得方程的解为,乙看错了方程(2)中的n值,得到的方程组的解为,求代数式的平方根,并求出原方程组的解
7.(2024七下·乳山期中)如图,在中,平分,交于点D,于点E,,,求的度数.
8.(2024七下·市南区期中) 如图,已知∠1=∠BDC,∠2+∠3=180°.
(1)问AD与CE平行吗?如果平行请说明理由.
(2)若CE⊥AE于E,DA平分∠BDC,∠FAB=68°,求∠1的度数.
9.(2024七下·济南期中) 学习整式的乘法时可以发现:用两种不同的方法表示同一个图形的面积,可以得到一个等式,进而可以利用得到的等式解决问题.
(1)如图,是由边长为,的正方形和长为、宽为的长方形拼成的大正方形,由图可得等式: ;
(2)知识迁移:
如图是用个小正方体和个小长方体拼成的一个大正方体,类比,用不同的方法表示这个大正方体的体积,则可得等式: ;
已知,,,利用中所得等式,求代数式的值.
10.(2024七下·冠县期中)某商场投入13800元资金购进甲、乙两种矿泉水共500箱,矿泉水的成本价和销售价如表所示:
类别/单价 成本价 销售价(元/箱)
甲 24 36
乙 33 48
(1)该商场购进甲、乙两种矿泉水各多少箱?
(2)全部售完500箱矿泉水,该商场共获得利润多少元?
11.(2024七下·牟平期中)“文明其精神,野蛮其体魄”,为进一步提升学生的健康水平,我市某校计划用760元购买14个体育用品,备选体育用品及单价如表:
备选体育用品 足球 篮球 排球
单价(元) 80 60 40
(1)若760元全部用来购买足球和排球,求足球和排球各购买的数量.
(2)若该校先用一部分资金购买了a个排球,再用剩下的资金购买了足球和篮球,且篮球和足球的个数相同,此时正好剩余80元,求a的值.
(3)由于篮球和排球都不够分配,该校再补充采购这两种球共花费了480元,其中这两种球都至少购进2个,则有几种补购方案?
12.(2024七下·济南期中) 中,,,过点作连接,,为平面内一动点.
(1)如图,若,则 .
(2)如图,点在上,且于,过点作于,为中点,连接并延长,交于点.
求证:≌;;
(3)如图,连接,,过点作于点,且满足,连接,,过点作于点,若,,,求线段的长度的取值范围.
13.(2024七下·瓜州期中)先阅读下面的内容,再解决问题,
例题:若 6n+9=0,求m和n的值.
∵ 6n+9=0
∴ 6n+9=0
∴
∴m+n=0,n 3=0
∴m= 3,n=3
问题:若 2xy+4y+4=0,求的值.
14.(2024七下·章丘期中)(1)如图1,已知,,可得 度;
(2)如图2,在(1)的条件下,如果平分,求度数;
(3)如图3,在(1)(2)的条件下,如果,则 度;
(4)尝试解决下面问题:如图4,,,是的平分线,,求的度数.
15.(2017七下·濮阳期中)如图,EF∥AD,AD∥BC,CE平分∠BCF,∠DAC=120°,∠ACF=20°,求∠FEC的度数.
16.(2024七下·荣成期中)如图,在中,边的垂直平分线交于点D,边的垂直半分线交于点E,与相交于点O,连接,若的周长为,的周长为.
(1)求线段的长;
(2)连接,求线段的长;
(3)若,求的度数.
17.(2024七下·市中区期中)(1)先化简,再求值:,其中,.
(2)已知,求代数式的值.
18.(2024七下·青岛期中)【知识回顾】我们在学习代数式求值时,遇到这样一类题:代数式的值与x的取值无关,求a的值.
通常的解题思路是:把x、y看作字母,a看作系数,合并同类项.因为代数式的值与x的取值无关,所以含x项的系数为0.
具体解题过程是:原式,
代数式的值与x的取值无关,
,解得.
【理解应用】(1)若关于x的多项式的值与x的取值无关,求m值;
(2)已知,,且的值与x的取值无关,求m的值;
【能力提升】(3)7张如图1的小长方形,长为a,宽为b,按照图2方式不重叠地放在大长方形内,大长方形中未被覆盖的两个部分都是长方形. 设右上角的面积为,左下角的面积为,当的长变化时,的值始终保持不变,求a与b的等量关系.
19.(2024七下·台儿庄期中)在图1中,三种不同大小的正方形与长方形,拼成了一个如图2所示的正方形.
(1)根据图 2 中的阴影部分面积关系直接写出下列代数式之间的数量关系:___________;
(2)已知,求和的值;
(3)已知,求的值.
20.(2024七下·莱芜期中)为了适合不同人群的口味,莱芜信誉楼超市购进了巧克力味、牛奶味的两种草莓进行销售.已知箱巧克力味的进价与箱牛奶味的进价的和为元,且每箱巧克力味的进价比每箱牛奶味的进价贵元.
(1)求每箱巧克力味的进价与每箱牛奶味的进价分别是多少元?
(2)如果某一天超市购进了巧克力味的草莓箱,且每箱价格提高出售,购进了牛奶味的草莓箱,且每箱价格提高出售,问这一天超市全部卖完利润为多少元?
21.(2024七下·乳山期中)如图,点在的边上,交于点,连接,,,,.求的度数.
22.(2024七下·桐柏期中)已知关于 x、y 的二元一次方程组.
(1)当时,解这个方程组;
(2)若,设,求S的取值范围.
23.(2024七下·兖州期中)如图,在长方形中,,,,,将长方形沿着直线折叠,使点C落在处,交于点E,求的度数.
24.(2024七下·宁津期中)(1)已知关于x,y的二元一次方程组的解互为相反数,求k的值.
(2)甲、乙两位同学在解方程组时,甲看错了第一个方程,解得 ,乙看错了第二个方程,解得 ,求+b3的值.
25.(2024七下·昌乐期中)如图,某小区有一块长为米,宽为米的长方形地块,物业公司计划在小区内修一条平行四边形小路,小路的底边宽为米,将阴影部分进行绿化.
(1)用含有、的式子表示绿化的总面积;
(2)若,,求出此时绿化的总面积.
26.(2024七下·济南期中) 如图,在中,,分别是的中线和高,是的角平分线.
(1)若的面积为,,求的长;
(2)若,,求的大小.
27.(2024七下·泰山期中)如图,直线交的边、于,交延长线于,若,,,求的度数.
28.(2024七下·潍城期中)我们知道,一般的数学公式,法则、定义可以正向运用,也可以逆向运用.例如,“同底数幂的乘法”“幂的乘方”“积的乘方”这几个法则的逆向运用表现为:;
;;其中m,n为正整数.结合以上材料解决下列问题.
(1)已知,请把a,b,c用“”连接起来;
(2)若,求的值;
(3)化简:.
29.(2024七下·莱芜期中)将的顶角A沿直线DE折叠(如图),点A的对应点为点,记为,为.
(1)如图1,当点A的对应点落在内部时,试探求与的数量关系,并说明理由;
(2)如图2,当点A的对应点落在外部时,与又有怎样的数量关系呢?请写出猜想,并给予证明.
30.(2024七下·湖北期中)如图,在△ABC中,∠1=∠2,点E、F、G分别在BC、AB、AC上,且EF⊥AB,DG∥BC,请判断CD与AB的位置关系,并说明理由.
答案解析部分
1.(1)解:由题意得,剩余钢板的面积为:
=a2+2ab+b2-a2-b2
=2ab
(2)解:∵原钢板的周长是40,
∴,
∴,
∴
∵,
∴
∴,
∴,
∴剩余钢板的面积.
(1)由图可知大图形的边长为(a+b),阴影部分面积=大图形面积(a+b)2减去两个小图形面积a2+b2得结果为2ab;
(2)由周长4(a+b)为40得到,再由,可得,再代入(1)中2ab的代数式进行计算即可.
(1)解:由题意得,剩余钢板的面积为:
.
(2)解:∵原钢板的周长是40,
∴,
∴,
∴
∵,
∴
∴,
∴,
∴剩余钢板的面积.
2.(1);
(2).
3.解:设小长方形的长为x,宽为y,
由题意得,,
解得,
∴阴影部分的正方形边长为,
∴阴影部分的面积为:.
本题主要考查了二元一次方程组的应用,设小长方形的长为x,宽为y,结合长加上宽的两倍等于15,长为宽的三倍,列出方程组,求得方程组的解,即可得到答案.
4.(1)解:,理由如下:
,
,
,
,
;
(2)解:由(1)知,
,
,
平分,
.
(1)由,得到,进而求得,结合同旁内角互补,两直线平行,即可证得;
(2)由(1)知,得到,求得,再由平分,结合,即可求解.
5.(1);
(2)
(3)
6.的平方根为;原方程组的解为:
7.
8.(1)解:AD∥CE,
理由:∵∠1=∠BDC,
∴AB∥CD,
∴∠2=∠ADC,
∵∠2+∠3=180°,
∴∠3+∠ADC=180°,
∴AD∥CE;
(2)解:∵CE⊥AE,
∴∠CEA=90°,
∵CE∥AD,
∴∠CEA=∠DAF=90°,
∵∠FAB=68°,
∴∠2=∠DAF﹣∠FAB=22°,
∴∠2=∠ADC=22°,
∵DA平分∠CDF,
∴∠CDF=2∠ADC=44°,
∴∠1=∠CDF=44°,
∴∠1的度数为44°.
(1)利用已知可得AB∥CD,从而可得∠2=∠ADC,进而可得∠3+∠ADC=180°,然后利用同旁内角互补,两直线平行可得AD∥CE,即可解答;
(2)根据垂直定义可得∠CEA=90°,再利用(1)的结论可得∠CEA=∠DAF=90°,从而可得∠2=22°,然后利用(1)的结论可得∠2=∠ADC=22°,再利用角平分线的定义可得∠CDF=2∠ADC=44°,即可解答。熟练掌握平行线的判定与性质是解题的关键。
9.(1)
(2)解:;由拼图可知,大立方体的边长为,因此这个大正方体的体积为;这个大立方体是由个部分拼成的,这个部分的体积和为,因此有,故答案为:由得,,答:代数式的值为.
解:(1)由图(1)可知,大正方形的边长为a+b,因此这个正方形的面积为(a+b)2;
而这个大正方形由四个部分拼成的,这四个部分的面积和为a2+2ab+b2,
因此有(a+b)2=a2+2ab+b2,
故答案为:(a+b)2=a2+2ab+b2;
(2)①由拼图可知,大立方体的边长为a+b,因此这个大正方体的体积为(a+b)3;
这个大立方体是由6个部分拼成的,这6个部分的体积和为a3+3a2b+3ab2+b3,
因此有(a+b)3=a3+3a2b+3ab2+b3,
故答案为:(a+b)3=a3+3a2b+3ab2+b3;
(1)从整体和部分两个方面分别用代数式表示它们的面积即可;
(2)①从整体和部分两个方面用代数式表示大正方体体积即可得出答案;②利用①中的结论代入计算即可。
10.(1)商场购进甲种矿泉水300箱,购进乙种矿泉水200箱;(2)该商场共获得利润6600元.
11.(1)足球购买5个、排球购买9个;(2)a的值为10;(3)则有3种补购方案,分别为篮球购2个,排球购9个,或篮球购4个,排球购6个,或篮球购6个,排球购3个.
12.(1)8
(2)解:,
,,
,
在和中,
,
≌,
,,
,,
,
,
为中点,
,
又,
在和中,
,
≌,
,,
,
;
(3)解:连接,如图,
,
,
,
在和中,
,
≌,
,
,
,
,
,
在中,,
,
.
当点,点,点共线时,最大值为,最小值为,
.
解:(1)∵∠ABC=90°,AB=BC,BC=4,
∴S△ABC=×AB BC=8.
∵AE⊥AB,BC⊥AB,
∴AE∥BC,
∴S△EBC=S△ABC=8,
故答案为:8;
(1)由平行线的性质可得S△AEC=S△ABE,即可求解;
(2)由“AAS”可证△ABF≌△BCM,利用全等三角形的性质可得AF=BM,BF=CM,由“ASA”可证△ADF≌△CDH,利用相似三角形的性质可得AF=HC,DF=DH,可得结论;
(3)由“SAS”可证△CBM≌△ABM',可得CM=AM',由三角形的三边关系定理可求解。
13.
14.(1);(2);(3)67.5;(4)
15.解:∵EF∥AD,AD∥BC,
∴EF∥BC,
∴∠ACB+∠DAC=180°,
∵∠DAC=120°,
∴∠ACB=60°,
又∵∠ACF=20°,
∴∠FCB=∠ACB﹣∠ACF=40°,
∵CE平分∠BCF,
∴∠BCE=20°,
∵EF∥BC,
∴∠FEC=∠ECB,
∴∠FEC=20°.
推出EF∥BC,根据平行线性质求出∠ACB,求出∠FCB,根据角平分线求出∠ECB,根据平行线的性质推出∠FEC=∠ECB,代入即可.
16.(1)解:∵边的垂直平分线交于点D,边的垂直半分线交于点E,∴,
∴,
∵的周长为,即,
∴;
(2)解:连接,
∵边的垂直平分线交于点D,边的垂直半分线交于点E,
∴,
∵的周长为,即,,
∴;
(3)解:∵,∴,
∵,
∴,
∴,
∴.
(1)由边的垂直平分线交于点D,边的垂直半分线交于点E,根据线段垂直平分线的性质,得到,再由的周长为,列出算式,即可求得BC的长,得到答案;
(2)根据线段垂直平分线的性质,得到,结合的周长为,列出算式,即可求得OA的长,得到答案;
继而求解即可;
(3)根据三角形内角和定理,得出,再由,得到,结合,即可求解.
17.解:(1)
,
当,时,
原式;
(2)
,
∵,
∴,
∴原式
.
(1)根据整式的混合运算法则,结合完全平方公式、多项式与多项式的乘法、整式的除法的运算,化简得到,再将,,代入代数式,计算求值,即可得到答案;
(2)根据整式的混合运算法则,结合平方差公式、单项式与多项式的乘法的运算,化简得到,再由 ,整体代入求值,即可得到答案.
18.(1);(2);(3)
19.(1)
(2),
(3)16
20.(1)解:设每箱巧克力味的进价为元,每箱牛奶味的进价为元
由题意可得,,
解得:,
答:每箱巧克力味的进价为元,每箱牛奶味的进价为元:
(2)解:依题意,(元);
答:这一天超市全部卖完利润为元.
(1)设每箱巧克力味的进价为元,每箱牛奶味的进价为元,根据题意,列出二元一次方程组,求得方程组的解,即可得到答案;
(2)根据(1)的结论,结合超市购进了巧克力味的草莓箱,且每箱价格提高出售,购进了牛奶味的草莓箱,且每箱价格提高出售,列出算式,进行计算,即可得到答案.
(1)解:设每箱巧克力味的进价为元,每箱牛奶味的进价为元
由题意可得,,
解得:,
答:每箱巧克力味的进价为元,每箱牛奶味的进价为元:
(2)解:依题意,(元);
答:这一天超市全部卖完利润为元.
21.
22.(1)
(2)
23.解:由折叠可知,,,∵,
∴,
∵,
∴,
∴.
本题主要考查了平行线的性质,以及折叠的性质,根据折叠的性质,得到,,由,得到,再由,结合,即可求解.
24.(1)解:
①×3﹣②得:8(x+y)=3k-12,即x+y,
由题意得:x+y=0,即,
解得k=4.
(2)根据题意,得:,
解得:,
则b3(﹣1)31.
(1)方程组两方程相减表示出x+y,根据x与y互为相反数得到x+y=0,求出k的值即可;
(2)将x=1、y=﹣1代入第二个方程、将x=﹣2、y=﹣6代入第一个方程,列出关于a、b的方程组,求出a、b的值,再代入求解可得.
25.(1)平方米
(2)196平方米
26.(1)解:是的中线,,
,
是的高,的面积为,
,
;
(2)解:在中,为它的一个外角,且,,
,
是的角平分线,
,
.
(1)利用面积法求解即可.
(2)求出∠ABC,再根据∠BAF=90°-∠ABC即可求解。
27.
28.(1)解:∵
∴
(2)解:,∵,
∴原式;
(3)解:
.
(1)根据题意,利用逆用幂的乘方公式,将幂变为指数相同的幂,然后比较大小,即可得到答案;
(2)根据题意,利用逆用同底数幂和幂的乘方运算法则,化简得到进,将, 代入代数式,进行计算,即可求解;
(3)根据题意,利用逆用积的乘方运算法则,先计算乘方,结合乘法的结合律,进行计算,即可求解.
(1)解:∵
∴
(2)解:,
∵,
∴原式;
(3)解:
.
29.(1)解:,理由见解析:
如图1,连接,
是的外角,
.
同理,.
.
由折叠性质得.
.
(2)解:,证明如下:
如图2,连接,
是的外角,
.
同理,.
.
由折叠性质得.
,
.
30.解:CD⊥AB.理由如下:
∴DG∥BC,
∴∠1=∠DCB,
∵∠1=∠2,
∴∠2=∠DCB,
∴CD∥EF,
∴∠CDB=∠EFB,
∵EF⊥AB,
∴∠EFB=90°,
∴∠CDB=90°,
∴CD⊥AB.
由平行线的性质和已知条件可证明CD∥EF,可求得∠CDB=90°,可判断CD⊥AB.
同课章节目录
