期中真题专项复习03 解答题(含答案)--2024-2025学年八年级数学下册(北京版)
文档属性
| 名称 | 期中真题专项复习03 解答题(含答案)--2024-2025学年八年级数学下册(北京版) |  | |
| 格式 | docx | ||
| 文件大小 | 1018.1KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北京版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-03-30 13:17:23 | ||
图片预览




文档简介
2024-2025学年八年级数学下册(北京版)
期中真题专项复习03 解答题
一、解答题
1.(2024八下·海淀期中)如图,四边形中,,,、分别是、的中点,,求的长.
2.(2024八下·海淀期中)已知:一次函数图象如图,
(1)求一次函数的解析式;
(2)若点P为该一次函数图象上一动点,且点A为该函数图象与x轴的交点,若S△OAP=2,求点P的坐标.
3.(2024八下·北京市期中)在平面直角坐标系中,将点向右平移4个单位长度,得到点,点在直线上.
(1)求的值和点的坐标;
(2)如果一次函数的图象与线段有公共点,则的取值范围是______.
4.(2024八下·海淀期中)在平面直角坐标系中,对于线段,若在坐标系中存在一点P使得四边形为菱形,则称线段为点O的“关联线段”.
(1)已知点,则下列点N中,可以使得成为点O的“关联线段”的是 ;
①②③
(2)已知点O的“关联线段”过点,且,求出线段的最大值;
(3)已知点,若存在点O的“关联线段”与直线有交点,直接写出k的取值范围为 .
5.(2024八下·平谷期中)在平面直角坐标系中,对于P、Q两点给出如下定义:若点P到两坐标轴的距离之和等于点Q到两坐标轴的距离之和,则称P、Q两点为垂距等点.如图所示P、Q两点即为垂距等点.
(1)已知点A的坐标为.
① 在点中,为点A的垂距等点的是 ;
② 若点B在y轴的负半轴上,且A、B两点为垂距等点,则点B的坐标为 ;
(2)直线与x轴交于点C,与y轴交于点D.
① 当E为线段上一点时,若在直线上存在点F,使得E、F两点为垂距等点,求n的取值范围.
② 已知正方形的边长为2,是对角线的交点,且正方形的任何一条边均与某条坐标轴垂直.当E为直线l上一动点时,若该正方形的边上存在点G,使得E、G两点为垂距等点,直接写出t的取值范围.
6.(2024八下·北京市期中)在平面直角坐标系中,对于点,,给出如下定义:当点,满足时,称点是点的等积点.已知点.
(1)在,,中,点的等积点是_____.
(2)点是点的等积点,点在轴上,以,,,为顶点的四边形是平行四边形,求点的坐标,写出求解过程.
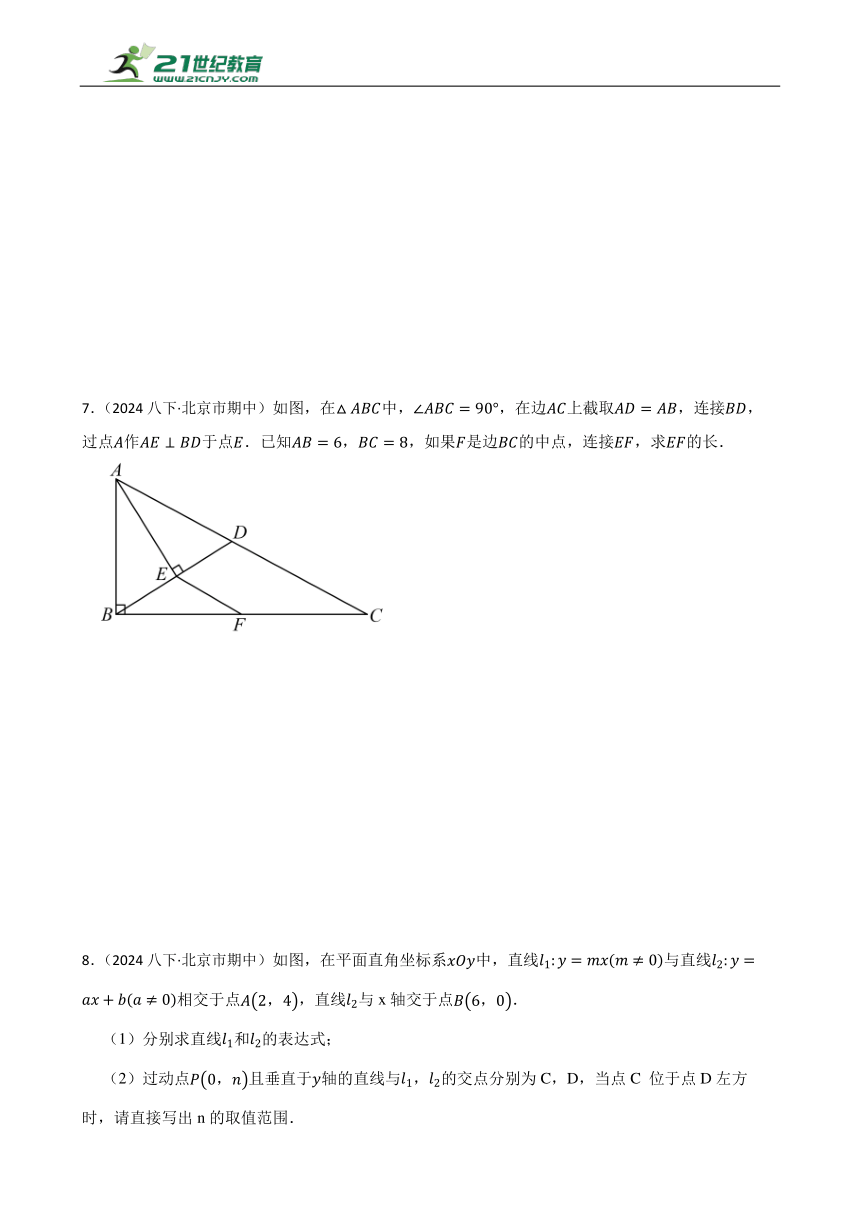
7.(2024八下·北京市期中)如图,在中,,在边上截取,连接,过点作于点.已知,,如果是边的中点,连接,求的长.
8.(2024八下·北京市期中)如图,在平面直角坐标系中,直线与直线相交于点,直线与x轴交于点.
(1)分别求直线和的表达式;
(2)过动点且垂直于轴的直线与,的交点分别为C,D,当点C 位于点D左方时,请直接写出n的取值范围.
9.(2024八下·北京市期中)已知直线经过点,.
(1)求直线的解析式;
(2)若直线与直线相交于点C,求点C的坐标;
(3)根据图象,写出关于x的不等式的解集.
10.(2024八下·北京市期中)在平面直角坐标系中,对于点,给出如下定义:若存在实数,,,使得且,则称点为以点和为端点的线段的等差点.
(1)若线段的两个端点坐标分别为和,则下列点是线段等差点的有__________;(填写序号即可)
①;②;③;④.
(2)点A,都在直线上,已知点A的横坐标为,,.
①如图1,当时,线段的等差点在线段上,求满足条件的点的坐标;
②如图2,点横坐标为2,以为对角线构造正方形,在正方形的边上(包括顶点)任取两点连接的线段中,若线段上存在其中某条线段的等差点,直接写出的取值范围__________.
11.(2024八下·北京市期中)已知一次函数.
(1)点在函数的图象上,求m的值.
(2)一次函数的图象与x轴、y轴分别交于点A、B.求点A、B的坐标.
(3)已知,求三角形的面积.
12.(2024八下·东城期中) 如图,正方形中,点是对角线上任意一点,连接,以点为垂足,过点作,交于点,连接,取的中点,连接.
(1)依题意补全图形;
(2)若,求的大小(用含的式子表示);
(3)用等式表示线段与之间的数量关系,并证明.
13.(2024八下·北京市期中)在平面直角坐标系中,一次函数的图象是由直线平移得到的,且经过点.
(1)求这个一次函数的解析式;
(2)当时,若对于x的每一个值,函数的值都大于一次函数的值,直接写出m的取值范围.
14.(2024八下·北京市期中)一次函数的图象经过点(-1,0)和(0,2).
(1)求这个一次函数的表达式;
(2)若直线与该一次函数的图象相交,且交点在第三象限,直接写出n的取值范围.
15.(2024八下·北京市期中)在平面直角坐标系中,对于点,如果点满足条件:以线段为对角线的正方形,且正方形的边分别与轴,轴平行,那么称点为点的“和谐点”,如下图所示.
已知点,,.
()已知点的坐标是.
①在,,中,是点的“和谐点”的是__________.
②已知点的坐标为,如果点为点的“和谐点”,求的值;
()已知点,如果线段上存在一个点,使得点是点的“和谐点”,直接写出的取值范围.
16.(2024八下·北京市期中)一次函数的图象如图所示.
(1)求k,b的值;
(2)求一次函数的图象与两坐标轴所围成三角形的面积;
(3)根据图象,直接写出不等式的解集.
17.(2024八下·丰台期中)在平面直角坐标系中,,,.若为矩形内(不包括边界)一点,过点分别作轴和轴的平行线,这两条平行线分矩形为四个小矩形,若这四个小矩形中有一个矩形的周长等于的长,则称点为矩形的矩宽点.
例如:下图中的点为矩形的一个矩宽点.
(1)在点,,中,矩形的矩宽点是______;
(2)若点为矩形的矩宽点,求的值.
18.(2024八下·朝阳期中)如图,在△ABC中,点D,点E分别是边AC,AB的中点,点F在线段DE上,AF=5,BF=12,AB=13,BC=19,求DF的长度.
19.(2024八下·朝阳期中)下面是小明设计的“利用已知矩形作一个内角为角的平行四边形”的尺规作图过程.
已知:矩形.
求作:平行四边形,使.
作法:如图,
①分别以A,B为圆心,以大于长为半径,在两侧作弧,分别交于点E,F;
②作直线;
③以点A为圆心,以长为半径作弧,交直线于点G,连接;
④以点G为圆心,以长为半径作弧,交直线于点H,连接.则四边形即为所求作的平行四边形.
根据小明设计的尺规作图过程,填空:
(1)的大小为______________;
(2)判定四边形是平行四边形的依据是______________________________.
20.(2024八下·北京市期中)在平面直角坐标系中,对于两个点,和图形,如果在图形上存在点,,可以重合)使得,那么称点与点是图形的一对平衡点.
(1)如图1,已知点,.
①设点与线段上一点的距离为,则的最小值是 ,最大值是 ;
②在,,这三个点中,与点是线段的一对平衡点的是 ;
(2)如图2,已知正方形的边长为2,一边平行于轴,对角线的交点为点,点的坐标为.若点在第一象限,且点与点是正方形的一对平衡点,求的取值范围;
(3)已知点,,某正方形对角线的交点为坐标原点,边长为.若线段上的任意两个点都是此正方形的一对平衡点,直接写出的取值范围.
21.(2024八下·西城期中)在平面直角坐标系中,对于直线和直线,在上取一点,在上取一点,若,以,为邻边作菱形,则菱形为的相关菱形,称为的相关菱角,的对边称为的相关菱边.特别地,当时,直线,即直线,代表轴.
例如:如图,,,,则菱形为的相关菱形,为的相关菱角,的对边为的相关菱边.
(1)若菱形是的相关菱形,则的相关菱角的度数是______;
(2)若菱形是的相关菱形,当点在的相关菱边上时,求的值;
(3)当的相关菱边与(其中)的相关菱边都经过点时,直接写出的取值范围.
22.(2024八下·东城期中) 在平面直角坐标系中,对于点和线段,其中,给出如下定义:若存在实数,使得,则称点是点关于线段的“中旋点”.
(1)已知点,点是关于线段的“中旋点”.
①若点的坐标是,则点的坐标是 ;
②若点的坐标是,点的坐标是,点是线段上任意一点,求线段长的取值范围;
(2)已知点,以为对角线构造正方形,在该正方形边上任取两点(包括顶点)构造线段,若直线上至少存在一个点关于的“中旋点”,直接写出的取值范围.
23.(2024八下·东城期中) 如图,在等腰中,.点为的中点,动点从点出发,沿着方向运动至点处停止,过点作,交于点.设点运动的路程为,点的距离为.
(1)请直接写出关于的函数表达式,并注明自变量的取值范围;
(2)在给定的平面直角坐标系中画出这个函数的图象,并写出该函数的一条性质;
(3)解决问题:当点的距离恰好是点运动的路程的2倍时,点的距离是 .
24.(2024八下·西城期中)下表是一次函数(,为常数,)中与的两组对应值.
0
(1)求这个一次函数的表达式;
(2)已知直线,当时,对于的每一个值,都有,直接写出的取值范围.
25.(2024八下·海淀期中)将平面直角坐标系中的一些点分成两类.每类至少包含两个点.对于同一类中的任意两点,,称与中的最大值为点M和点N的“垂平距离”,记作.将各类中任意两点间的最大“垂平距离”记为该类的“星内距离”,两个“星内距离”的最大值定义为这种分类的“星系距离”.
如图,,,,,.
(1)点A, B,E,O中,与点C的“垂平距离”为3的点是______;
(2)①点P是平面内的一个动点,若将点B,D,P分在同一类时,该类的“星内距离”是4,则动点P所构成图形的面积为______;
②已知直线上恰好存在唯一的一个点Q,满足将点B,D,Q分在同一类时,该类的“星内距离”是4,求b的值;
(3)已知直线l平行于,与x轴交于点,若l上的任意一点R均满足将点A,B,C,D,E,R分为两类时,所能得到的最小的“星系距离”大于4,请直接写出t的取值范围______.
26.(2024八下·海淀期中)如图,四边形是菱形,对角线,交于点O,E是延长线上一点,且,,,求的长度.
27.(2024八下·北京市期中)在平面直角坐标系中,对于P,Q两点给出如下定义:若点P到两条坐标轴的距离之和等于点Q到两条坐标轴的距离之和,则称P,Q两点为和谐点.例如,图1中的P,Q两点即为和谐点.
(1)已知点.
①在点中,点A的和谐点是 ;
②若点B在y轴上,且A,B两点为和谐点,则点B的坐标是 ;
(2)已知点,点,连接,点M为线段上一点.
①经过点且垂直于x轴的直线记作直线l,若在直线l上存在点N,使得M,N两点为和谐点,则n的取值范围是 ;
②若点,点,在以线段为斜边的等腰直角三角形的某条边上存在点K,使得M,K两点为和谐点,则m的取值范围是 .
28.(2024八下·西城期中)在平面直角坐标系中,对于正方形和它边上的动点P,以为斜边作等腰且O,P,Q三点按顺时针排列,则称点Q是点P关于正方形的“相关点”.已知,,,,这里.
(1)如图1,若,当点P在正方形的边上运动时,设点P关于正方形的“相关点”为点Q.
①若点Q恰好也在正方形的边上,这样的点P的个数是_________;
A.0个;B.1个;C.2个;D.4个
②设点P的横坐标为p,求点Q的坐标;
(2)当时,对于正方形和它边上的动点P,则所有点P关于正方形的“相关点”组成图形的面积为_________;
(3)如图2,,,当点P在正方形的四条边上运动时,若线段上有且只有一个P关于正方形的“相关点”,直接写出a的取值范围.
29.(2024八下·东城期中)如图1,点A(a,b)在平面直角坐标系xOy中,点A到坐标轴的垂线段AB,AC与坐标轴围成矩形OBAC,当这个矩形的一组邻边长的和与积相等时,点A称作“垂点”,矩形称作“垂点矩形”.
(1)在点P(1,2),Q(2,-2),N(,-1)中,是“垂点”的点为 ;
(2)点M(-4,m)是第三象限的“垂点”,直接写出m的值 ;
(3)如果“垂点矩形”的面积是,且“垂点”位于第二象限,写出满足条件的“垂点”的坐标 ;
(4)如图2,平面直角坐标系的原点O是正方形DEFG的对角线的交点,当正方形DEFG的边上存在“垂点”时,GE的最小值为 .
30.(2024八下·海淀期中)中,点是边上一点(不与B、C组合),连结,若P是的中点,则称点为中边的“有缘点”.其中,若、,则点的坐标为.
已知
(1)点、、、中,是中边的“有缘点”的有______.
(2)已知中,,点在轴上方,若第二、四象限的角平分线上存在边的“有缘点”,求的取值范围;
(3)中,在轴上,点的横坐标为t,交轴于点,交轴于点,且Q、M分别是、的中点,假设三边的“有缘点”组成图形,若图形的面积满足:,直接写出t的值.
答案解析部分
1.
2.(1)y=﹣x+1;(2)P点坐标为(﹣3,4)或(5,﹣4).
3.(1),
(2)
4.(1)①③
(2)
(3)
5.(1)①,②
(2)①②或
6.(1)和
(2)或
7.2
8.(1)(2)
9.(1)
(2)
(3)
10.(1)①④
(2)①或;②或.
11.(1)6
(2)点的坐标为,点的坐标为
(3)4
12.(1)解:补全图形如下:
(2)解: 四边形为正方形
为的中点,
(3)解:
证明:连接,如图所示:
四边形为正方形
在和中,
,
为的中点,
由(2)可知
为等腰直角三角形,
(1)根据文字描述,补全图形即可;
(2)首先根据正方形的性质得出∠ADB=45°,进而得出∠ODE=45°-α,然后再根据直角三角形斜边上的中线,得出OE=OD,即可得出∠POE=90°-2α;
(3)。 连接,如图所示: 首先根据SAS可证得△ADE≌△CDE,从而得出AE=CE,然后通过证明△AOE是等腰直角三角形,得出,等量代换为CE=.
13.(1)
(2)
14.(1);(2).
15.()①,;②或;(2)或
16.(1),
(2)4
(3)
17.(1)和
(2)或
18.3
19.(1)
(2)一组对边平行且相等的四边形是平行四边形
20.(1)①3,;②
(2)
(3)
21.(1)或
(2)的值为
(3)
22.(1)解:①②设直线解析式为,∴,∴,∴直线解析式为,
∵点是线段上任意一点,∴可设,
∵点是关于线段的“中旋点”.∴,∴,∴,
∴,
令,∴,
∵,∴,
∴当时,的值随着m增大而减小,
∴当时,有最大值,当时,有最小值8,∴;
(2)或.
解:(2)如图2-1所示,当点M在上,点N在上时,
设,
∴,
∴,
∴
当点M固定时,点N从点C运动到点D,那么点Q的纵坐标不变,横坐标从0运动到,
当点N固定时,点M从点A运动到点D,那么点Q的横坐标不变,纵坐标从0运动到2,
∴当点M在上,点N在上时,点Q的运动区域即为四个点组成的正方形区域(不包括顶点E),
同理由对称性可知当点M与点N在正方形的邻边上时,点Q的运动区域为组成的正方形区域(不包括四个顶点);
如图2-2所示,当点M在上,点N在上时,
设,
∴,
∴,
∴
当点M固定时,点N从点C运动到点D,那么点Q的纵坐标不变,横坐标从运动到,
当点N固定时,点M从点A运动到点D,那么点Q的纵坐标不变,横坐标从运动到,
∴当点M在上,点N在上时,点Q的运动区域即为线段;
同理由对称性可知当点M在上,点N在上时,点Q的运动区域为线段;
当点M和点N都在上时,设,同理得,
∴此时点Q的运功区域为线段(不包括端点),
由对称性可知,当M、N在同一边时,点Q的运动区域即为线段(不包括端点),
综上所述,点Q的运动区域为组成的正方形区域(不包括四个顶点);
∵直线上至少存在一个点关于的“中旋点”,
∴直线与组成的正方形区域至少有一个交点(不包括顶点),
当直线恰好经过时,,解得;
当直线恰好经过时,,解得;
∴如图2-3所示,当或直线与组成的正方形区域至少有一个交点(不包括顶点),
∴若直线上至少存在一个点关于的“中旋点”,则或.
(1)①根据中旋点的定义,即可得出点Q的坐标;
②首先利用待定系数法求出直线EF的解析式,可设点P, 根据中旋点的定义,可得点Q(2-m,4-m),可得:PQ2=8(m-2)2+8,根据二次函数的性质,即可求得PQ的取值范围;
(2)首先分成两种情况讨论:当点M在上,点N在上时,可得点Q的运动区域为组成的正方形区域(不包括四个顶点);当点M在上,点N在上时,点Q的运动区域为组成的正方形区域(不包括四个顶点);综上所述,点Q的运动区域为组成的正方形区域(不包括四个顶点);然后根据直线上至少存在一个点关于的“中旋点”,可得直线与组成的正方形区域至少有一个交点(不包括顶点),当直线恰好经过时,,解得;当直线恰好经过时,,解得;结合图象可得出若直线上至少存在一个点关于的“中旋点”,则或.
23.(1)解:,
,
点为的中点,
,
当点在上运动时,,
,
由题意得:,则,
,,
,
;
当点在上运动时,,
,
由题意得:,则,
,,
,
;
综上所述,;
(2)解:画出函数图象如图所示:
,
由图象可得,函数的最大值为;
(3)
解:(3)可分成两种情况:①当当点在上运动时,,2x=,解得:x=,所以y=,即 点的距离是;② 当点在上运动时,, 2x=,解得:x=(不合题意,舍去);综上可得: 点的距离是;
故答案为:;
(1)关于的函数表达式 可分为两段来表示:① 当点在上运动时,,可得出BP=2+x, 根据含30°锐角的直角三角形的性质,可得出; ② 当点在上运动时,, 可得出CP=6-x,从而根据含30°锐角的直角三角形的性质,可得出;综上所述,可得出:;
(2)根据界点,分别描出点(0,1),(2,2)及(6,0),连接(0,1),(2,2),再连接(2,2),(6,0),即可得出函数图象,观察函数图象,可得函数的最大值为2;
(3)可分成两种情况:①当当点在上运动时,,2x=,解得:x=,所以y=,即 点的距离是;② 当点在上运动时,, 2x=,解得:x=(不合题意,舍去);综上可得: 点的距离是;
24.(1)
(2)
25.(1)A
(2)①;②或7
(3)或
26.
27.(1)①;②或
(2)①;②或
28.(1)①C;②点的坐标为
(2)24
(3)或或
29.(1)Q;(2)-;(3)(-4,),(-,4);(4)8
30.(1),
(2)
(3)或
期中真题专项复习03 解答题
一、解答题
1.(2024八下·海淀期中)如图,四边形中,,,、分别是、的中点,,求的长.
2.(2024八下·海淀期中)已知:一次函数图象如图,
(1)求一次函数的解析式;
(2)若点P为该一次函数图象上一动点,且点A为该函数图象与x轴的交点,若S△OAP=2,求点P的坐标.
3.(2024八下·北京市期中)在平面直角坐标系中,将点向右平移4个单位长度,得到点,点在直线上.
(1)求的值和点的坐标;
(2)如果一次函数的图象与线段有公共点,则的取值范围是______.
4.(2024八下·海淀期中)在平面直角坐标系中,对于线段,若在坐标系中存在一点P使得四边形为菱形,则称线段为点O的“关联线段”.
(1)已知点,则下列点N中,可以使得成为点O的“关联线段”的是 ;
①②③
(2)已知点O的“关联线段”过点,且,求出线段的最大值;
(3)已知点,若存在点O的“关联线段”与直线有交点,直接写出k的取值范围为 .
5.(2024八下·平谷期中)在平面直角坐标系中,对于P、Q两点给出如下定义:若点P到两坐标轴的距离之和等于点Q到两坐标轴的距离之和,则称P、Q两点为垂距等点.如图所示P、Q两点即为垂距等点.
(1)已知点A的坐标为.
① 在点中,为点A的垂距等点的是 ;
② 若点B在y轴的负半轴上,且A、B两点为垂距等点,则点B的坐标为 ;
(2)直线与x轴交于点C,与y轴交于点D.
① 当E为线段上一点时,若在直线上存在点F,使得E、F两点为垂距等点,求n的取值范围.
② 已知正方形的边长为2,是对角线的交点,且正方形的任何一条边均与某条坐标轴垂直.当E为直线l上一动点时,若该正方形的边上存在点G,使得E、G两点为垂距等点,直接写出t的取值范围.
6.(2024八下·北京市期中)在平面直角坐标系中,对于点,,给出如下定义:当点,满足时,称点是点的等积点.已知点.
(1)在,,中,点的等积点是_____.
(2)点是点的等积点,点在轴上,以,,,为顶点的四边形是平行四边形,求点的坐标,写出求解过程.
7.(2024八下·北京市期中)如图,在中,,在边上截取,连接,过点作于点.已知,,如果是边的中点,连接,求的长.
8.(2024八下·北京市期中)如图,在平面直角坐标系中,直线与直线相交于点,直线与x轴交于点.
(1)分别求直线和的表达式;
(2)过动点且垂直于轴的直线与,的交点分别为C,D,当点C 位于点D左方时,请直接写出n的取值范围.
9.(2024八下·北京市期中)已知直线经过点,.
(1)求直线的解析式;
(2)若直线与直线相交于点C,求点C的坐标;
(3)根据图象,写出关于x的不等式的解集.
10.(2024八下·北京市期中)在平面直角坐标系中,对于点,给出如下定义:若存在实数,,,使得且,则称点为以点和为端点的线段的等差点.
(1)若线段的两个端点坐标分别为和,则下列点是线段等差点的有__________;(填写序号即可)
①;②;③;④.
(2)点A,都在直线上,已知点A的横坐标为,,.
①如图1,当时,线段的等差点在线段上,求满足条件的点的坐标;
②如图2,点横坐标为2,以为对角线构造正方形,在正方形的边上(包括顶点)任取两点连接的线段中,若线段上存在其中某条线段的等差点,直接写出的取值范围__________.
11.(2024八下·北京市期中)已知一次函数.
(1)点在函数的图象上,求m的值.
(2)一次函数的图象与x轴、y轴分别交于点A、B.求点A、B的坐标.
(3)已知,求三角形的面积.
12.(2024八下·东城期中) 如图,正方形中,点是对角线上任意一点,连接,以点为垂足,过点作,交于点,连接,取的中点,连接.
(1)依题意补全图形;
(2)若,求的大小(用含的式子表示);
(3)用等式表示线段与之间的数量关系,并证明.
13.(2024八下·北京市期中)在平面直角坐标系中,一次函数的图象是由直线平移得到的,且经过点.
(1)求这个一次函数的解析式;
(2)当时,若对于x的每一个值,函数的值都大于一次函数的值,直接写出m的取值范围.
14.(2024八下·北京市期中)一次函数的图象经过点(-1,0)和(0,2).
(1)求这个一次函数的表达式;
(2)若直线与该一次函数的图象相交,且交点在第三象限,直接写出n的取值范围.
15.(2024八下·北京市期中)在平面直角坐标系中,对于点,如果点满足条件:以线段为对角线的正方形,且正方形的边分别与轴,轴平行,那么称点为点的“和谐点”,如下图所示.
已知点,,.
()已知点的坐标是.
①在,,中,是点的“和谐点”的是__________.
②已知点的坐标为,如果点为点的“和谐点”,求的值;
()已知点,如果线段上存在一个点,使得点是点的“和谐点”,直接写出的取值范围.
16.(2024八下·北京市期中)一次函数的图象如图所示.
(1)求k,b的值;
(2)求一次函数的图象与两坐标轴所围成三角形的面积;
(3)根据图象,直接写出不等式的解集.
17.(2024八下·丰台期中)在平面直角坐标系中,,,.若为矩形内(不包括边界)一点,过点分别作轴和轴的平行线,这两条平行线分矩形为四个小矩形,若这四个小矩形中有一个矩形的周长等于的长,则称点为矩形的矩宽点.
例如:下图中的点为矩形的一个矩宽点.
(1)在点,,中,矩形的矩宽点是______;
(2)若点为矩形的矩宽点,求的值.
18.(2024八下·朝阳期中)如图,在△ABC中,点D,点E分别是边AC,AB的中点,点F在线段DE上,AF=5,BF=12,AB=13,BC=19,求DF的长度.
19.(2024八下·朝阳期中)下面是小明设计的“利用已知矩形作一个内角为角的平行四边形”的尺规作图过程.
已知:矩形.
求作:平行四边形,使.
作法:如图,
①分别以A,B为圆心,以大于长为半径,在两侧作弧,分别交于点E,F;
②作直线;
③以点A为圆心,以长为半径作弧,交直线于点G,连接;
④以点G为圆心,以长为半径作弧,交直线于点H,连接.则四边形即为所求作的平行四边形.
根据小明设计的尺规作图过程,填空:
(1)的大小为______________;
(2)判定四边形是平行四边形的依据是______________________________.
20.(2024八下·北京市期中)在平面直角坐标系中,对于两个点,和图形,如果在图形上存在点,,可以重合)使得,那么称点与点是图形的一对平衡点.
(1)如图1,已知点,.
①设点与线段上一点的距离为,则的最小值是 ,最大值是 ;
②在,,这三个点中,与点是线段的一对平衡点的是 ;
(2)如图2,已知正方形的边长为2,一边平行于轴,对角线的交点为点,点的坐标为.若点在第一象限,且点与点是正方形的一对平衡点,求的取值范围;
(3)已知点,,某正方形对角线的交点为坐标原点,边长为.若线段上的任意两个点都是此正方形的一对平衡点,直接写出的取值范围.
21.(2024八下·西城期中)在平面直角坐标系中,对于直线和直线,在上取一点,在上取一点,若,以,为邻边作菱形,则菱形为的相关菱形,称为的相关菱角,的对边称为的相关菱边.特别地,当时,直线,即直线,代表轴.
例如:如图,,,,则菱形为的相关菱形,为的相关菱角,的对边为的相关菱边.
(1)若菱形是的相关菱形,则的相关菱角的度数是______;
(2)若菱形是的相关菱形,当点在的相关菱边上时,求的值;
(3)当的相关菱边与(其中)的相关菱边都经过点时,直接写出的取值范围.
22.(2024八下·东城期中) 在平面直角坐标系中,对于点和线段,其中,给出如下定义:若存在实数,使得,则称点是点关于线段的“中旋点”.
(1)已知点,点是关于线段的“中旋点”.
①若点的坐标是,则点的坐标是 ;
②若点的坐标是,点的坐标是,点是线段上任意一点,求线段长的取值范围;
(2)已知点,以为对角线构造正方形,在该正方形边上任取两点(包括顶点)构造线段,若直线上至少存在一个点关于的“中旋点”,直接写出的取值范围.
23.(2024八下·东城期中) 如图,在等腰中,.点为的中点,动点从点出发,沿着方向运动至点处停止,过点作,交于点.设点运动的路程为,点的距离为.
(1)请直接写出关于的函数表达式,并注明自变量的取值范围;
(2)在给定的平面直角坐标系中画出这个函数的图象,并写出该函数的一条性质;
(3)解决问题:当点的距离恰好是点运动的路程的2倍时,点的距离是 .
24.(2024八下·西城期中)下表是一次函数(,为常数,)中与的两组对应值.
0
(1)求这个一次函数的表达式;
(2)已知直线,当时,对于的每一个值,都有,直接写出的取值范围.
25.(2024八下·海淀期中)将平面直角坐标系中的一些点分成两类.每类至少包含两个点.对于同一类中的任意两点,,称与中的最大值为点M和点N的“垂平距离”,记作.将各类中任意两点间的最大“垂平距离”记为该类的“星内距离”,两个“星内距离”的最大值定义为这种分类的“星系距离”.
如图,,,,,.
(1)点A, B,E,O中,与点C的“垂平距离”为3的点是______;
(2)①点P是平面内的一个动点,若将点B,D,P分在同一类时,该类的“星内距离”是4,则动点P所构成图形的面积为______;
②已知直线上恰好存在唯一的一个点Q,满足将点B,D,Q分在同一类时,该类的“星内距离”是4,求b的值;
(3)已知直线l平行于,与x轴交于点,若l上的任意一点R均满足将点A,B,C,D,E,R分为两类时,所能得到的最小的“星系距离”大于4,请直接写出t的取值范围______.
26.(2024八下·海淀期中)如图,四边形是菱形,对角线,交于点O,E是延长线上一点,且,,,求的长度.
27.(2024八下·北京市期中)在平面直角坐标系中,对于P,Q两点给出如下定义:若点P到两条坐标轴的距离之和等于点Q到两条坐标轴的距离之和,则称P,Q两点为和谐点.例如,图1中的P,Q两点即为和谐点.
(1)已知点.
①在点中,点A的和谐点是 ;
②若点B在y轴上,且A,B两点为和谐点,则点B的坐标是 ;
(2)已知点,点,连接,点M为线段上一点.
①经过点且垂直于x轴的直线记作直线l,若在直线l上存在点N,使得M,N两点为和谐点,则n的取值范围是 ;
②若点,点,在以线段为斜边的等腰直角三角形的某条边上存在点K,使得M,K两点为和谐点,则m的取值范围是 .
28.(2024八下·西城期中)在平面直角坐标系中,对于正方形和它边上的动点P,以为斜边作等腰且O,P,Q三点按顺时针排列,则称点Q是点P关于正方形的“相关点”.已知,,,,这里.
(1)如图1,若,当点P在正方形的边上运动时,设点P关于正方形的“相关点”为点Q.
①若点Q恰好也在正方形的边上,这样的点P的个数是_________;
A.0个;B.1个;C.2个;D.4个
②设点P的横坐标为p,求点Q的坐标;
(2)当时,对于正方形和它边上的动点P,则所有点P关于正方形的“相关点”组成图形的面积为_________;
(3)如图2,,,当点P在正方形的四条边上运动时,若线段上有且只有一个P关于正方形的“相关点”,直接写出a的取值范围.
29.(2024八下·东城期中)如图1,点A(a,b)在平面直角坐标系xOy中,点A到坐标轴的垂线段AB,AC与坐标轴围成矩形OBAC,当这个矩形的一组邻边长的和与积相等时,点A称作“垂点”,矩形称作“垂点矩形”.
(1)在点P(1,2),Q(2,-2),N(,-1)中,是“垂点”的点为 ;
(2)点M(-4,m)是第三象限的“垂点”,直接写出m的值 ;
(3)如果“垂点矩形”的面积是,且“垂点”位于第二象限,写出满足条件的“垂点”的坐标 ;
(4)如图2,平面直角坐标系的原点O是正方形DEFG的对角线的交点,当正方形DEFG的边上存在“垂点”时,GE的最小值为 .
30.(2024八下·海淀期中)中,点是边上一点(不与B、C组合),连结,若P是的中点,则称点为中边的“有缘点”.其中,若、,则点的坐标为.
已知
(1)点、、、中,是中边的“有缘点”的有______.
(2)已知中,,点在轴上方,若第二、四象限的角平分线上存在边的“有缘点”,求的取值范围;
(3)中,在轴上,点的横坐标为t,交轴于点,交轴于点,且Q、M分别是、的中点,假设三边的“有缘点”组成图形,若图形的面积满足:,直接写出t的值.
答案解析部分
1.
2.(1)y=﹣x+1;(2)P点坐标为(﹣3,4)或(5,﹣4).
3.(1),
(2)
4.(1)①③
(2)
(3)
5.(1)①,②
(2)①②或
6.(1)和
(2)或
7.2
8.(1)(2)
9.(1)
(2)
(3)
10.(1)①④
(2)①或;②或.
11.(1)6
(2)点的坐标为,点的坐标为
(3)4
12.(1)解:补全图形如下:
(2)解: 四边形为正方形
为的中点,
(3)解:
证明:连接,如图所示:
四边形为正方形
在和中,
,
为的中点,
由(2)可知
为等腰直角三角形,
(1)根据文字描述,补全图形即可;
(2)首先根据正方形的性质得出∠ADB=45°,进而得出∠ODE=45°-α,然后再根据直角三角形斜边上的中线,得出OE=OD,即可得出∠POE=90°-2α;
(3)。 连接,如图所示: 首先根据SAS可证得△ADE≌△CDE,从而得出AE=CE,然后通过证明△AOE是等腰直角三角形,得出,等量代换为CE=.
13.(1)
(2)
14.(1);(2).
15.()①,;②或;(2)或
16.(1),
(2)4
(3)
17.(1)和
(2)或
18.3
19.(1)
(2)一组对边平行且相等的四边形是平行四边形
20.(1)①3,;②
(2)
(3)
21.(1)或
(2)的值为
(3)
22.(1)解:①②设直线解析式为,∴,∴,∴直线解析式为,
∵点是线段上任意一点,∴可设,
∵点是关于线段的“中旋点”.∴,∴,∴,
∴,
令,∴,
∵,∴,
∴当时,的值随着m增大而减小,
∴当时,有最大值,当时,有最小值8,∴;
(2)或.
解:(2)如图2-1所示,当点M在上,点N在上时,
设,
∴,
∴,
∴
当点M固定时,点N从点C运动到点D,那么点Q的纵坐标不变,横坐标从0运动到,
当点N固定时,点M从点A运动到点D,那么点Q的横坐标不变,纵坐标从0运动到2,
∴当点M在上,点N在上时,点Q的运动区域即为四个点组成的正方形区域(不包括顶点E),
同理由对称性可知当点M与点N在正方形的邻边上时,点Q的运动区域为组成的正方形区域(不包括四个顶点);
如图2-2所示,当点M在上,点N在上时,
设,
∴,
∴,
∴
当点M固定时,点N从点C运动到点D,那么点Q的纵坐标不变,横坐标从运动到,
当点N固定时,点M从点A运动到点D,那么点Q的纵坐标不变,横坐标从运动到,
∴当点M在上,点N在上时,点Q的运动区域即为线段;
同理由对称性可知当点M在上,点N在上时,点Q的运动区域为线段;
当点M和点N都在上时,设,同理得,
∴此时点Q的运功区域为线段(不包括端点),
由对称性可知,当M、N在同一边时,点Q的运动区域即为线段(不包括端点),
综上所述,点Q的运动区域为组成的正方形区域(不包括四个顶点);
∵直线上至少存在一个点关于的“中旋点”,
∴直线与组成的正方形区域至少有一个交点(不包括顶点),
当直线恰好经过时,,解得;
当直线恰好经过时,,解得;
∴如图2-3所示,当或直线与组成的正方形区域至少有一个交点(不包括顶点),
∴若直线上至少存在一个点关于的“中旋点”,则或.
(1)①根据中旋点的定义,即可得出点Q的坐标;
②首先利用待定系数法求出直线EF的解析式,可设点P, 根据中旋点的定义,可得点Q(2-m,4-m),可得:PQ2=8(m-2)2+8,根据二次函数的性质,即可求得PQ的取值范围;
(2)首先分成两种情况讨论:当点M在上,点N在上时,可得点Q的运动区域为组成的正方形区域(不包括四个顶点);当点M在上,点N在上时,点Q的运动区域为组成的正方形区域(不包括四个顶点);综上所述,点Q的运动区域为组成的正方形区域(不包括四个顶点);然后根据直线上至少存在一个点关于的“中旋点”,可得直线与组成的正方形区域至少有一个交点(不包括顶点),当直线恰好经过时,,解得;当直线恰好经过时,,解得;结合图象可得出若直线上至少存在一个点关于的“中旋点”,则或.
23.(1)解:,
,
点为的中点,
,
当点在上运动时,,
,
由题意得:,则,
,,
,
;
当点在上运动时,,
,
由题意得:,则,
,,
,
;
综上所述,;
(2)解:画出函数图象如图所示:
,
由图象可得,函数的最大值为;
(3)
解:(3)可分成两种情况:①当当点在上运动时,,2x=,解得:x=,所以y=,即 点的距离是;② 当点在上运动时,, 2x=,解得:x=(不合题意,舍去);综上可得: 点的距离是;
故答案为:;
(1)关于的函数表达式 可分为两段来表示:① 当点在上运动时,,可得出BP=2+x, 根据含30°锐角的直角三角形的性质,可得出; ② 当点在上运动时,, 可得出CP=6-x,从而根据含30°锐角的直角三角形的性质,可得出;综上所述,可得出:;
(2)根据界点,分别描出点(0,1),(2,2)及(6,0),连接(0,1),(2,2),再连接(2,2),(6,0),即可得出函数图象,观察函数图象,可得函数的最大值为2;
(3)可分成两种情况:①当当点在上运动时,,2x=,解得:x=,所以y=,即 点的距离是;② 当点在上运动时,, 2x=,解得:x=(不合题意,舍去);综上可得: 点的距离是;
24.(1)
(2)
25.(1)A
(2)①;②或7
(3)或
26.
27.(1)①;②或
(2)①;②或
28.(1)①C;②点的坐标为
(2)24
(3)或或
29.(1)Q;(2)-;(3)(-4,),(-,4);(4)8
30.(1),
(2)
(3)或
同课章节目录
