期中真题专项复习02 填空题(含答案)--2024-2025学年八年级数学下册(北京版)
文档属性
| 名称 | 期中真题专项复习02 填空题(含答案)--2024-2025学年八年级数学下册(北京版) |  | |
| 格式 | docx | ||
| 文件大小 | 628.3KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北京版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-03-30 13:30:19 | ||
图片预览



文档简介
2024-2025学年八年级数学下册(北京版)
期中真题专项复习02 填空题
一、填空题
1.(2024八下·北京市期中)在正方形ABCD中,E是对角线AC上一点,且AE=AB,则∠EBC的度数是 .
2.(2024八下·丰台期中)如图,菱形ABCD的面积为12,其中对角线AC长为4,则对角线BD的长为 .
3.(2024八下·海淀期中)对于一次函数,下表中给出3组自变量和相应的函数值.
则的值为 .
4.(2024八下·香洲期中)如图,在中,点、分别是边、的中点,,则 .
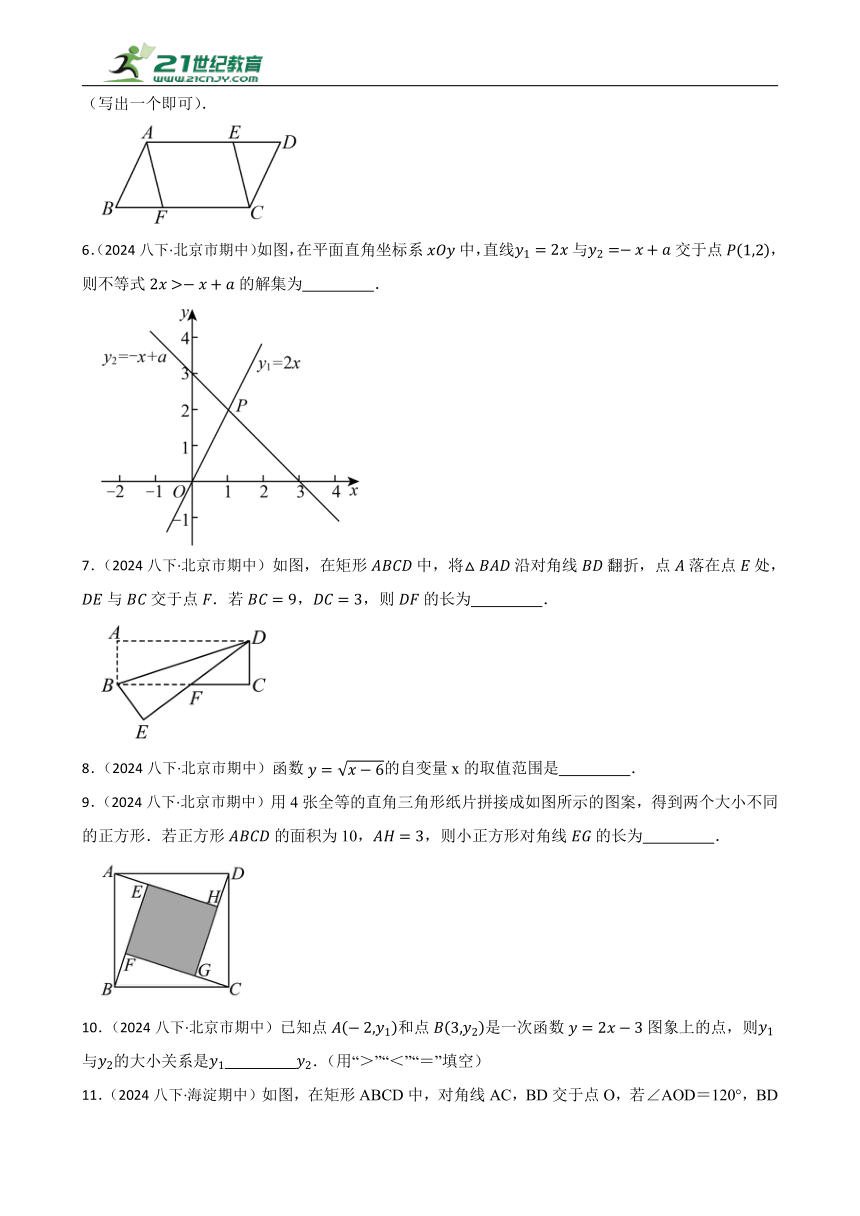
5.(2024八下·平谷期中)如图,在中,E,F分别是边AD,BC上的点,连接AF,CE,只需添加一个条件即可证明四边形AFCE是平行四边形,这个条件可以是 (写出一个即可).
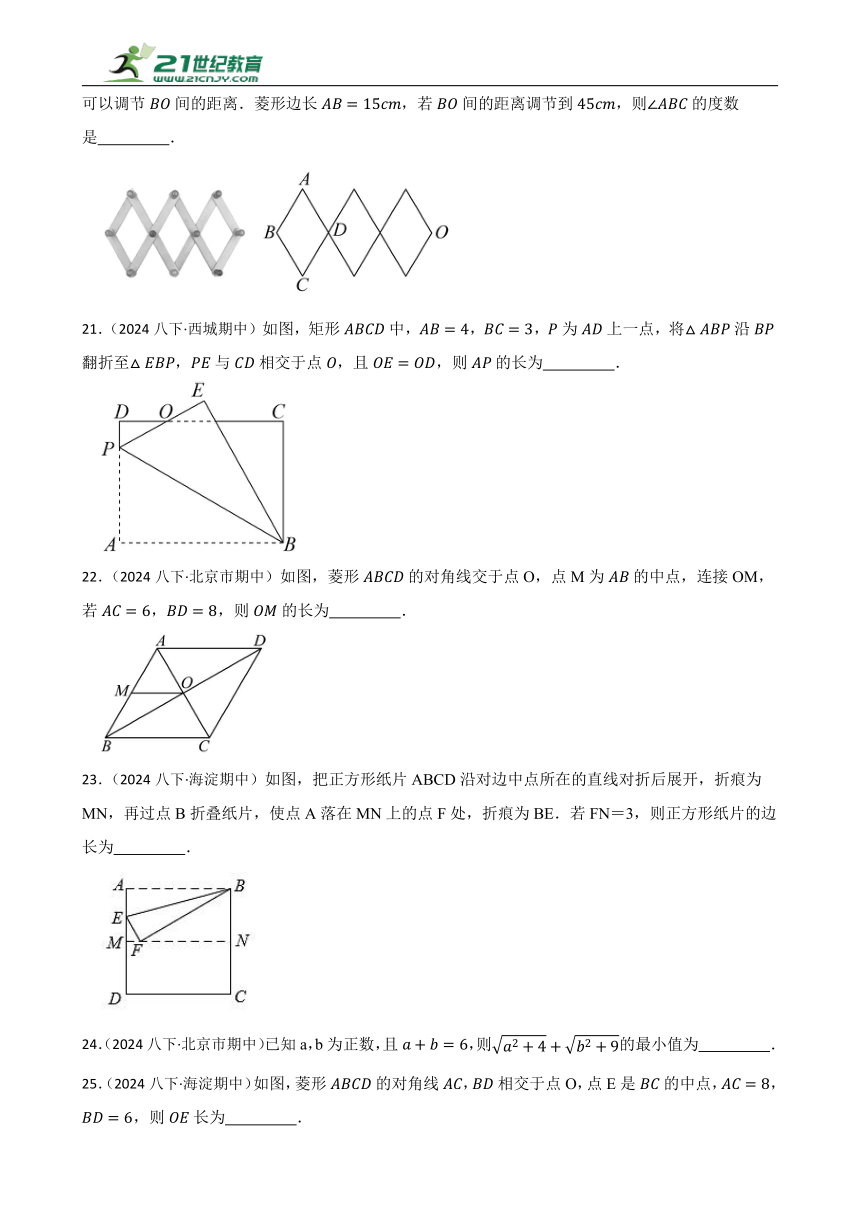
6.(2024八下·北京市期中)如图,在平面直角坐标系中,直线与交于点,则不等式的解集为 .
7.(2024八下·北京市期中)如图,在矩形中,将沿对角线翻折,点落在点处,与交于点.若,,则的长为 .
8.(2024八下·北京市期中)函数的自变量x的取值范围是 .
9.(2024八下·北京市期中)用4张全等的直角三角形纸片拼接成如图所示的图案,得到两个大小不同的正方形.若正方形的面积为10,,则小正方形对角线的长为 .
10.(2024八下·北京市期中)已知点和点是一次函数图象上的点,则与的大小关系是 .(用“>”“<”“=”填空)
11.(2024八下·海淀期中)如图,在矩形ABCD中,对角线AC,BD交于点O,若∠AOD=120°,BD=6,则AB的长为 .
12.(2024八下·北京市期中)如图,点在线段上,是等边三角形,四边形是正方形.
(1) ;
(2)点是线段上的一个动点,连接,.若,,则的最小值为 .
13.(2024八下·海淀期中)直线与在平面直角坐标系中的位置如图所示,则不等式组的解集为 .
14.(2024八下·海淀期中)如图,在平面直角坐标系中,矩形的顶点A,B,C的坐标分别为,,,轴,则点D的坐标为 .
15.(2024八下·海淀期中)如图,在矩形ABCD,BE平分,交AD于点E,F是BE的中点,G是BC的中点,连按EC,若,,则FG的长为 .
16.(2024八下·海淀期中)已知菱形中对角线相交于点O,添加条件 可使菱形成为正方形.
17.(2024八下·东城期中)在数学课上,老师提出如下问题:
已知:如图1,线段,求作:平行四边形.
小明的作法如下:
如图2:(1)以点C为圆心,长为半径画弧;
(2)以点A为圆心,长为半径画弧;
(3)两弧在上方交于点D,连接,四边形为所求作平行四边形.
老师说:“小明的作法正确.”
请回答:四边形是平行四边形的依据是 .
18.(2024八下·东城期中)在菱形中,若,周长是16,则菱形的面积是 .
19.(2024八下·北京市期中)如图,在正方形ABCD内部作等边△CDE,连接BD.则的度数为 .
20.(2024八下·北京市期中)如图所示的木制活动衣帽架,是由三个全等的菱形构成,根据实际需要可以调节间的距离.菱形边长,若间的距离调节到,则的度数是 .
21.(2024八下·西城期中)如图,矩形中,,,为上一点,将沿翻折至,与相交于点,且,则的长为 .
22.(2024八下·北京市期中)如图,菱形的对角线交于点O,点M为的中点,连接OM,若,,则的长为 .
23.(2024八下·海淀期中)如图,把正方形纸片ABCD沿对边中点所在的直线对折后展开,折痕为MN,再过点B折叠纸片,使点A落在MN上的点F处,折痕为BE.若FN=3,则正方形纸片的边长为 .
24.(2024八下·北京市期中)已知a,b为正数,且,则的最小值为 .
25.(2024八下·海淀期中)如图,菱形的对角线,相交于点O,点E是的中点,,,则长为 .
26.(2024八下·东城期中)如图,在 ABCD中,再添加一个条件 (写出一个即可), ABCD是矩形(图形中不再添加辅助线)
27.(2024八下·北京市期中)如图,正方形中,点E是对角线上的一点,且,连接,,则的度数为 .
28.(2024八下·海淀期中)如图,在平面直角坐标系中,长方形MNPQ的顶点M,N分别在轴,轴正半轴上滑动,顶点P、Q在第一象限,若MN=4,PN=2,在滑动过程中,点P与坐标原点O的距离的最大值是 .
29.(2024八下·北京市期中)如图,在中,,在边上截取,连接,过点A作于点E.已知,如果F是边的中点,连接,那么的长是 .
30.(2024八下·平凉期中)如图,A,B两点被池塘隔开,在AB外选一点C,连接AC和BC.分别取AC,BC的中点D,E,测得D,E两点间的距离为20m,则A,B两点间的距离为 m.
31.(2024八下·北京市期中)如图,在中,再添加一个条件(写出一个即可),使是菱形.(图形中不再添加辅助线)
32.(2024八下·北京市期中)如图,在平行四边形中,,,平分,是对角线上的一个动点,点是边上的一个动点,则的最小值是 .
33.(2024八下·北京市期中)如图,在矩形ABCD中,点E在边AD上,EF平分∠AEC交BC于点F.若AD=7,AE=CD=3,则BF的长为 .
34.(2024八下·北京市期中)在平面直角坐标系中,直线与直线相交于点,则 .
35.(2024八下·平谷期中)函数中,自变量的取值范围是 ;函数中,自变量的取值范围是 .
36.(2024八下·北京市期中)如图,以菱形的顶点O为原点,对角线所在直线为x轴建立平面直角坐标系,若,点C的坐标为,则点A的坐标为 .
37.(2024八下·昌平期中)如图,在矩形ABCD中,AD=3,CD=4,点P是AC上一个动点(点P与点A,C不重合),过点P分别作PE⊥BC于点E,PF∥BC交AB于点F,连接EF,则EF的最小值为 .
38.(2024八下·西城期中)如图,点P是正方形的对角线上一点,,,垂足分别为点E,F,连接,,若,则 .
39.(2024八下·西城期中)如图,把矩形沿直线向上折叠,使点落在点的位置上,交于点,若,,则的长为 .
40.(2024八下·西城期中)如果一次函数的图象经过第三象限,且与y轴正半轴相交,那么k 0,b 0.
41.(2024八下·东城期中) 如图,已知菱形的两条对角线分别为6和8,点是边的中点,点是边上一点,点是对角线上一点,则的最小值为 .
42.(2024八下·东城期中) 如图,在正方形中,点分别是边上的点,连接,若,则的度数为 .
43.(2024八下·东城期中) 如图,在平面直角坐标系中,点的坐标分别为,若直线与有公共点,则的取值范围为 .
44.(2024八下·北京市期中)如图,直线与直线交于点,则关于x的不等式的解集是 .
45.(2024八下·海淀期中)如图,,,和都是等边三角形,F为中点,交于G点,下列结论中,正确的结论是 .
①;②;③四边形是菱形;④.
46.(2024八下·北京市期中)已知邻边长分别为1,的平行四边形纸片,且有,如图那样折一下,剪下一个边长等于1的菱形(称为第一次操作);再把剩下的平行四边形如图那样折一下,剪下一个边长等于此时平行四边形一边长的菱形(称为第二次操作);再把剩下的平行四边形如此反复操作下去.若在第三次操作后,剩下的平行四边形为菱形,则的值是 .
47.(2024八下·北京市期中)如图,直线与直线交于点P,则不等式的解集为 .
48.(2024八下·北京市期中)如图,在矩形中,过对角线中点的两条直线交、于E、F,交、于点H、G,若矩形的边长为4和2,则图中阴影部分的面积为 .
49.(2024八下·北京市期中)如图,在菱形中,对角线与交于点,若,,则菱形的面积等于 .
50.(2024八下·北京市期中)如图,请给矩形ABCD添加一个条件,使它成为正方形,则此条件可以为 .
答案解析部分
1.22.5°
2.
3.
4.4
5.(答案不唯一)
6.
7.
8.x≥6.
9.
10.<
11.3
12.;
13.
14.
15.5
16.或
17.两组对边分别相等的四边形是平行四边形
18.
19.15°
20.
21.2.4
22.
23.
24.
25.
26.AC=BD
27.
28.
29.1
30.40
解:∵点D,E分别是BC和AC的中点,
∴DE是△ABC的中位线,DE=20m,
∴AB=2DE=2×20=40(m).
故答案为:40.
先判断出DE是△ABC的中位线,再根据三角形的中位线平行于第三边并且等于第三边的一半可得AB=2DE,问题得解.
31.(答案不唯一)
32.
33.2
34.3
35.;
36.
37.
38.
39.
40.;
41.
解:作点M关于直线BD的对称点M',过点M'作M'N'⊥CD于点N',交BD于点P',则点P在点P'的位置时,PM+PN的值最小,且最小值为线段M'N'的长度。即AB和CD这一组对边之间的距离。连接AC交BD于点O,连接P'M。
∵四边形ABCD是菱形,
∴∠AOB=90°,AO=3,BO=4,
∴AB=5,
∴S菱形ABCD=,
∴5M'N'=,
∴M'N'=.
即的最小值为 :。
故答案为:。
首先作点M关于直线BD的对称点M',过点M'作M'N'⊥CD于点N',交BD于点P',则点P在点P'的位置时,PM+PN的值最小,且最小值为线段M'N'的长度。即AB和CD这一组对边之间的距离。连接AC交BD于点O,连接P'M。首先根据菱形的性质,结合勾股定理得出AB=5,然后再根据菱形面积的两种不同求法,即可得出PM+PN的最小值。
42.
解:经过点C作CF∥MN,交AD于点F,
∵四边形ABCD是正方形,
∴BC=CD,MF∥CN,∠BCE=∠D=90°,
又∵CF∥MN,
∴四边形MNCF是平行四边形,
∴CF=MN,
又∵BE=MN,
∴BE=CF,
∴Rt△BCE≌Rt△CDF,
∴∠CBE=∠DCE=30°,
∴∠DFC=90°-30°=60°,
∵CF∥MN,
∴∠DMN=∠DFC=60°。
故答案为:60°。
经过点C作CF∥MN,交AD于点F,首先根据HL证明Rt△BCE≌Rt△CDF,得出∠CBE=∠DCE=30°,进而得出∠DFC°=60°,然后再根据平行线的性质,即可得出∠DMN=60°。
43.
解:当直线 经过点C时:3=2+b,解得b=1;当直线 经过点B时:1=4+b,解得:b=-3,
所以的取值范围为 :。
根据两个界点,即可求得b的取值范围。
44.
45.①②④
46.或4或或.
47.x>1
48.4
49.
50.
期中真题专项复习02 填空题
一、填空题
1.(2024八下·北京市期中)在正方形ABCD中,E是对角线AC上一点,且AE=AB,则∠EBC的度数是 .
2.(2024八下·丰台期中)如图,菱形ABCD的面积为12,其中对角线AC长为4,则对角线BD的长为 .
3.(2024八下·海淀期中)对于一次函数,下表中给出3组自变量和相应的函数值.
则的值为 .
4.(2024八下·香洲期中)如图,在中,点、分别是边、的中点,,则 .
5.(2024八下·平谷期中)如图,在中,E,F分别是边AD,BC上的点,连接AF,CE,只需添加一个条件即可证明四边形AFCE是平行四边形,这个条件可以是 (写出一个即可).
6.(2024八下·北京市期中)如图,在平面直角坐标系中,直线与交于点,则不等式的解集为 .
7.(2024八下·北京市期中)如图,在矩形中,将沿对角线翻折,点落在点处,与交于点.若,,则的长为 .
8.(2024八下·北京市期中)函数的自变量x的取值范围是 .
9.(2024八下·北京市期中)用4张全等的直角三角形纸片拼接成如图所示的图案,得到两个大小不同的正方形.若正方形的面积为10,,则小正方形对角线的长为 .
10.(2024八下·北京市期中)已知点和点是一次函数图象上的点,则与的大小关系是 .(用“>”“<”“=”填空)
11.(2024八下·海淀期中)如图,在矩形ABCD中,对角线AC,BD交于点O,若∠AOD=120°,BD=6,则AB的长为 .
12.(2024八下·北京市期中)如图,点在线段上,是等边三角形,四边形是正方形.
(1) ;
(2)点是线段上的一个动点,连接,.若,,则的最小值为 .
13.(2024八下·海淀期中)直线与在平面直角坐标系中的位置如图所示,则不等式组的解集为 .
14.(2024八下·海淀期中)如图,在平面直角坐标系中,矩形的顶点A,B,C的坐标分别为,,,轴,则点D的坐标为 .
15.(2024八下·海淀期中)如图,在矩形ABCD,BE平分,交AD于点E,F是BE的中点,G是BC的中点,连按EC,若,,则FG的长为 .
16.(2024八下·海淀期中)已知菱形中对角线相交于点O,添加条件 可使菱形成为正方形.
17.(2024八下·东城期中)在数学课上,老师提出如下问题:
已知:如图1,线段,求作:平行四边形.
小明的作法如下:
如图2:(1)以点C为圆心,长为半径画弧;
(2)以点A为圆心,长为半径画弧;
(3)两弧在上方交于点D,连接,四边形为所求作平行四边形.
老师说:“小明的作法正确.”
请回答:四边形是平行四边形的依据是 .
18.(2024八下·东城期中)在菱形中,若,周长是16,则菱形的面积是 .
19.(2024八下·北京市期中)如图,在正方形ABCD内部作等边△CDE,连接BD.则的度数为 .
20.(2024八下·北京市期中)如图所示的木制活动衣帽架,是由三个全等的菱形构成,根据实际需要可以调节间的距离.菱形边长,若间的距离调节到,则的度数是 .
21.(2024八下·西城期中)如图,矩形中,,,为上一点,将沿翻折至,与相交于点,且,则的长为 .
22.(2024八下·北京市期中)如图,菱形的对角线交于点O,点M为的中点,连接OM,若,,则的长为 .
23.(2024八下·海淀期中)如图,把正方形纸片ABCD沿对边中点所在的直线对折后展开,折痕为MN,再过点B折叠纸片,使点A落在MN上的点F处,折痕为BE.若FN=3,则正方形纸片的边长为 .
24.(2024八下·北京市期中)已知a,b为正数,且,则的最小值为 .
25.(2024八下·海淀期中)如图,菱形的对角线,相交于点O,点E是的中点,,,则长为 .
26.(2024八下·东城期中)如图,在 ABCD中,再添加一个条件 (写出一个即可), ABCD是矩形(图形中不再添加辅助线)
27.(2024八下·北京市期中)如图,正方形中,点E是对角线上的一点,且,连接,,则的度数为 .
28.(2024八下·海淀期中)如图,在平面直角坐标系中,长方形MNPQ的顶点M,N分别在轴,轴正半轴上滑动,顶点P、Q在第一象限,若MN=4,PN=2,在滑动过程中,点P与坐标原点O的距离的最大值是 .
29.(2024八下·北京市期中)如图,在中,,在边上截取,连接,过点A作于点E.已知,如果F是边的中点,连接,那么的长是 .
30.(2024八下·平凉期中)如图,A,B两点被池塘隔开,在AB外选一点C,连接AC和BC.分别取AC,BC的中点D,E,测得D,E两点间的距离为20m,则A,B两点间的距离为 m.
31.(2024八下·北京市期中)如图,在中,再添加一个条件(写出一个即可),使是菱形.(图形中不再添加辅助线)
32.(2024八下·北京市期中)如图,在平行四边形中,,,平分,是对角线上的一个动点,点是边上的一个动点,则的最小值是 .
33.(2024八下·北京市期中)如图,在矩形ABCD中,点E在边AD上,EF平分∠AEC交BC于点F.若AD=7,AE=CD=3,则BF的长为 .
34.(2024八下·北京市期中)在平面直角坐标系中,直线与直线相交于点,则 .
35.(2024八下·平谷期中)函数中,自变量的取值范围是 ;函数中,自变量的取值范围是 .
36.(2024八下·北京市期中)如图,以菱形的顶点O为原点,对角线所在直线为x轴建立平面直角坐标系,若,点C的坐标为,则点A的坐标为 .
37.(2024八下·昌平期中)如图,在矩形ABCD中,AD=3,CD=4,点P是AC上一个动点(点P与点A,C不重合),过点P分别作PE⊥BC于点E,PF∥BC交AB于点F,连接EF,则EF的最小值为 .
38.(2024八下·西城期中)如图,点P是正方形的对角线上一点,,,垂足分别为点E,F,连接,,若,则 .
39.(2024八下·西城期中)如图,把矩形沿直线向上折叠,使点落在点的位置上,交于点,若,,则的长为 .
40.(2024八下·西城期中)如果一次函数的图象经过第三象限,且与y轴正半轴相交,那么k 0,b 0.
41.(2024八下·东城期中) 如图,已知菱形的两条对角线分别为6和8,点是边的中点,点是边上一点,点是对角线上一点,则的最小值为 .
42.(2024八下·东城期中) 如图,在正方形中,点分别是边上的点,连接,若,则的度数为 .
43.(2024八下·东城期中) 如图,在平面直角坐标系中,点的坐标分别为,若直线与有公共点,则的取值范围为 .
44.(2024八下·北京市期中)如图,直线与直线交于点,则关于x的不等式的解集是 .
45.(2024八下·海淀期中)如图,,,和都是等边三角形,F为中点,交于G点,下列结论中,正确的结论是 .
①;②;③四边形是菱形;④.
46.(2024八下·北京市期中)已知邻边长分别为1,的平行四边形纸片,且有,如图那样折一下,剪下一个边长等于1的菱形(称为第一次操作);再把剩下的平行四边形如图那样折一下,剪下一个边长等于此时平行四边形一边长的菱形(称为第二次操作);再把剩下的平行四边形如此反复操作下去.若在第三次操作后,剩下的平行四边形为菱形,则的值是 .
47.(2024八下·北京市期中)如图,直线与直线交于点P,则不等式的解集为 .
48.(2024八下·北京市期中)如图,在矩形中,过对角线中点的两条直线交、于E、F,交、于点H、G,若矩形的边长为4和2,则图中阴影部分的面积为 .
49.(2024八下·北京市期中)如图,在菱形中,对角线与交于点,若,,则菱形的面积等于 .
50.(2024八下·北京市期中)如图,请给矩形ABCD添加一个条件,使它成为正方形,则此条件可以为 .
答案解析部分
1.22.5°
2.
3.
4.4
5.(答案不唯一)
6.
7.
8.x≥6.
9.
10.<
11.3
12.;
13.
14.
15.5
16.或
17.两组对边分别相等的四边形是平行四边形
18.
19.15°
20.
21.2.4
22.
23.
24.
25.
26.AC=BD
27.
28.
29.1
30.40
解:∵点D,E分别是BC和AC的中点,
∴DE是△ABC的中位线,DE=20m,
∴AB=2DE=2×20=40(m).
故答案为:40.
先判断出DE是△ABC的中位线,再根据三角形的中位线平行于第三边并且等于第三边的一半可得AB=2DE,问题得解.
31.(答案不唯一)
32.
33.2
34.3
35.;
36.
37.
38.
39.
40.;
41.
解:作点M关于直线BD的对称点M',过点M'作M'N'⊥CD于点N',交BD于点P',则点P在点P'的位置时,PM+PN的值最小,且最小值为线段M'N'的长度。即AB和CD这一组对边之间的距离。连接AC交BD于点O,连接P'M。
∵四边形ABCD是菱形,
∴∠AOB=90°,AO=3,BO=4,
∴AB=5,
∴S菱形ABCD=,
∴5M'N'=,
∴M'N'=.
即的最小值为 :。
故答案为:。
首先作点M关于直线BD的对称点M',过点M'作M'N'⊥CD于点N',交BD于点P',则点P在点P'的位置时,PM+PN的值最小,且最小值为线段M'N'的长度。即AB和CD这一组对边之间的距离。连接AC交BD于点O,连接P'M。首先根据菱形的性质,结合勾股定理得出AB=5,然后再根据菱形面积的两种不同求法,即可得出PM+PN的最小值。
42.
解:经过点C作CF∥MN,交AD于点F,
∵四边形ABCD是正方形,
∴BC=CD,MF∥CN,∠BCE=∠D=90°,
又∵CF∥MN,
∴四边形MNCF是平行四边形,
∴CF=MN,
又∵BE=MN,
∴BE=CF,
∴Rt△BCE≌Rt△CDF,
∴∠CBE=∠DCE=30°,
∴∠DFC=90°-30°=60°,
∵CF∥MN,
∴∠DMN=∠DFC=60°。
故答案为:60°。
经过点C作CF∥MN,交AD于点F,首先根据HL证明Rt△BCE≌Rt△CDF,得出∠CBE=∠DCE=30°,进而得出∠DFC°=60°,然后再根据平行线的性质,即可得出∠DMN=60°。
43.
解:当直线 经过点C时:3=2+b,解得b=1;当直线 经过点B时:1=4+b,解得:b=-3,
所以的取值范围为 :。
根据两个界点,即可求得b的取值范围。
44.
45.①②④
46.或4或或.
47.x>1
48.4
49.
50.
同课章节目录
